032、数据结构之代码时间复杂度和空间复杂度的判断：从入门到实战

作为程序员，我们每天都在和代码打交道，但你是否遇到过这些问题：同样是实现一个功能，别人的代码处理10万条数据秒级完成，你的却要卡几分钟？面试时被问"这个算法的复杂度是多少"，瞬间大脑空白？其实，解决这些问题的核心，就是掌握「时间复杂度」和「空间复杂度」的判断能力------这是衡量代码效率的"通用标尺"，也是程序员的核心基础技能。

今天这篇文章，从基础概念到实战案例，带你彻底搞懂复杂度判断，不管是新手入门、进阶提升，还是面试备考，都能有所收获。

一、开篇引入：为什么复杂度判断是程序员的必备技能？

1.1 先搞懂：我们为什么需要学复杂度判断？

在实际开发中，"能跑通"只是代码的基本要求，"跑得高效"才是核心竞争力。而复杂度判断，正是解决「如何快速评估代码效率」的核心工具------它能帮我们避免因代码效率低下导致的系统卡顿、资源浪费，甚至高并发场景下的崩溃问题。

再说说应用场景，复杂度判断几乎贯穿程序员的整个职业生涯：

算法设计与优化：面试算法题求解、竞赛算法优化，都离不开复杂度分析；

项目开发评审：评估新增代码对系统性能的影响，提前规避性能隐患；

性能瓶颈排查：快速定位系统中"拖后腿"的低效代码模块；

数据结构选型：比如数组和链表、哈希表和红黑树，到底选哪个？复杂度分析是关键依据。

更重要的是，它是校招面试的"必考点"------几乎所有算法题都会追问"时间复杂度和空间复杂度是多少"，日常开发中性能优化也是刚需。可以说，没掌握复杂度判断，很难写出高效、可扩展的代码。

1.2 读这篇文章，你能收获什么？

这篇文章不搞晦涩理论，主打"实用落地"，读完你能：

搞懂时间复杂度、空间复杂度的核心定义，不会再被"大O记号"搞晕；

掌握复杂度的判断逻辑，能独立分析常见数据结构（数组、链表、树等）和核心算法（排序、查找、递归）的复杂度；

通过实战案例，学会用复杂度分析指导算法选型和代码优化；

避开复杂度判断的常见坑，面试时能清晰阐述分析思路。

适用人群也很广：零基础新手可以搭建基础能力，进阶开发者能巩固复杂场景分析逻辑，面试备考者可针对性强化高频考点。

1.3 阅读指引：按需选择，高效学习

文章结构清晰，不同需求的读者可以针对性阅读：

新手入门：优先读「基础铺垫」「核心内容-基础用法」，先掌握基本概念和简单场景判断；

进阶提升：重点看「核心内容-进阶用法」「实战案例」，攻克复杂场景分析；

面试备考：额外关注「常见问题与避坑指南」，搞定面试高频考点。

二、基础铺垫：先搞懂这3个核心概念

在学习判断方法前，我们先扫清基础障碍，搞懂几个核心术语------不用怕，这里全是通俗解释，没有学术化表述。

2.1 核心概念：用"人话"讲清楚

1）时间复杂度（Time Complexity）

通俗说：数据量变大时，代码执行变慢的程度。

专业定义：描述算法执行时间随输入数据规模增长的变化趋势。比如"处理100条数据要1秒，处理1000条数据要10秒"，这就是典型的"线性增长"趋势。

2）空间复杂度（Space Complexity）

通俗说：数据量变大时，代码占用内存变多的程度。

专业定义：描述算法执行过程中所需存储空间随输入数据规模增长的变化趋势。比如"处理100条数据占100MB内存，处理1000条数据占1GB内存"，也是线性增长趋势。

3）大O记号（Big O Notation）

这是表示复杂度的"通用语言"，核心是「忽略次要因素，聚焦核心趋势」。

比如一段代码的执行时间表达式是"2n + 3"（n是输入数据规模）：

常数项3：表示固定的初始化时间，和n无关，可忽略；
系数2：表示每次循环的固定耗时，不同硬件（CPU）执行速度不同，可忽略；
最终简化为O(n)，只保留影响趋势的最高次项n。

常见的复杂度等级（从高效到低效）：

O(1) ＜ O(logn) ＜ O(n) ＜ O(nlogn) ＜ O(n²) ＜ O(2ⁿ)。

容易混淆的3个区别

时间复杂度 ≠ 实际执行时间：前者是趋势评估，后者受硬件影响（比如高性能CPU跑O(n)代码更快）；
空间复杂度 ≠ 内存占用量：前者是趋势评估，后者是具体场景的真实内存使用；
最坏复杂度 ≠ 平均复杂度：日常开发/面试优先分析「最坏复杂度」（保证系统极端情况下的稳定性），平均复杂度仅用于理论分析。

2.2 前置知识与环境准备

1）前置技能要求

不用太复杂，掌握这些基础就够了：

基本编程语法：循环、条件判断、函数调用、递归；
基础数据结构：数组、链表、栈、队列的基本操作；
简单数学逻辑：能理解"指数增长比线性增长快""对数增长比线性增长慢"。

2）环境准备

复杂度分析不用特殊环境，纸笔就能梳理逻辑；如果想验证结果，准备这些即可：

任意编程语言开发环境（Python/Java/C++均可，本文用Python示例，语法简洁）；
可选工具：时间统计（Python的time模块）、内存监控（Java的VisualVM），用于验证复杂度趋势。

三、核心内容：复杂度判断的方法与实例

这是本文的核心部分，我们从"理论逻辑"到"实操案例"，一步步掌握复杂度判断------记住：判断的核心是「找核心操作/核心空间，分析与n的关系」。

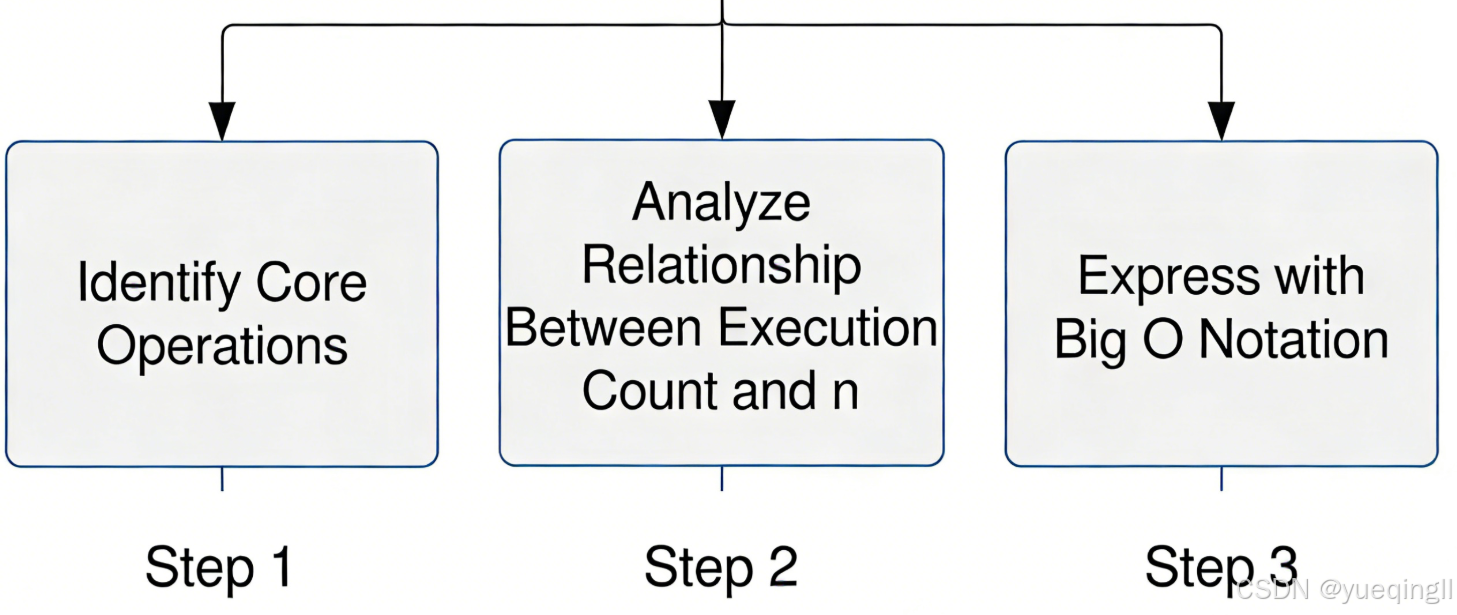
3.1 核心原理：判断的通用流程

1）时间复杂度判断流程

定位「核心操作」：找代码中执行次数最多的操作（比如循环内的比较、计算、赋值）；
分析执行次数与n的关系：核心操作执行了多少次？随n怎么变化？
用大O记号表示：忽略常数项、低次项、系数，保留最高次项。

2）空间复杂度判断流程

梳理「占用空间的变量/数据结构」：比如数组、链表、递归栈、哈希表；
分析空间大小与n的关系：这些结构的大小随n怎么变化？
用大O记号表示：忽略常数级空间（比如固定的临时变量），保留与n相关的项。

3.2 基础用法：常见复杂度的判断实例

下面结合具体代码，讲解5种常见复杂度的判断方法------代码都可直接运行，建议动手验证一下。

1）常数阶 O(1)：执行次数固定，与n无关

特征：无循环、无递归，核心操作执行次数固定。

复制代码

# 示例：获取数组的第一个元素和最后一个元素
def get_first_and_last(arr):
    first = arr[0]  # 核心操作1：1次
    last = arr[-1]  # 核心操作2：1次
    return first, last

# 分析：不管数组长度n是10还是1000，核心操作都只执行2次，与n无关
# 时间复杂度：O(1)，空间复杂度：O(1)（仅用2个临时变量）

2）线性阶 O(n)：执行次数与n成正比

特征：单重循环，核心操作执行次数随n线性增长。

复制代码

# 示例：遍历数组，计算所有元素的和
def sum_array(arr):
    total = 0  # 初始化：1次
    for num in arr:
        total += num  # 核心操作：执行n次（n是数组长度）
    return total

# 分析：核心操作（累加）执行次数 = 数组长度n，随n线性增长
# 时间复杂度：O(n)，空间复杂度：O(1)（仅用1个临时变量total）

3）平方阶 O(n²)：执行次数与n²成正比

特征：双重嵌套循环，核心操作执行次数是n×n。

复制代码

# 示例：冒泡排序（简化版）
def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(n - i - 1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]  # 核心操作：最多执行n×n次
    return arr

# 分析：外层循环n次，内层循环最多n次，核心操作执行次数≈n²
# 时间复杂度：O(n²)，空间复杂度：O(1)（仅用临时变量i、j）

4）对数阶 O(logn)：执行次数随n呈对数增长

特征：循环中每次将问题规模缩小一半（比如二分查找），执行次数是log₂n（可简化为logn）。

复制代码

# 示例：二分查找（有序数组）
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2  # 核心操作：执行log₂n次
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

# 分析：每次循环将查找范围缩小一半，比如n=8时，最多执行3次（log₂8=3）
# 时间复杂度：O(logn)，空间复杂度：O(1)（仅用left、right、mid3个变量）

5）线性对数阶 O(nlogn)：循环嵌套对数操作

特征：外层线性循环（O(n)），内层对数循环（O(logn)），总复杂度是n×logn。常见于高效排序算法（归并排序、快速排序）。

复制代码

# 示例：归并排序（核心逻辑）
def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    # 拆分（对数操作：执行logn次）
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    # 合并（线性操作：执行n次）
    return merge(left, right)

def merge(left, right):
    res = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    res.extend(left[i:])
    res.extend(right[j:])
    return res

# 分析：拆分过程是logn层，每层合并是n次操作，总执行次数≈nlogn
# 时间复杂度：O(nlogn)，空间复杂度：O(n)（需要额外数组存储合并结果）

3.3 进阶用法：复杂场景的复杂度分析

掌握基础用法后，我们来看几个进阶场景------这些也是面试中常考的难点。

1）递归算法的复杂度分析

递归算法的时间复杂度：看「递归树的总节点数」；空间复杂度：看「递归深度」（递归栈的层数）。

复制代码

# 示例：递归实现斐波那契数列
def fib(n):
    if n <= 1:
        return n
    return fib(n-1) + fib(n-2)

# 时间复杂度分析：
# 递归树中每个节点对应一次函数调用，总节点数≈2ⁿ（指数增长）
# 时间复杂度：O(2ⁿ)

# 空间复杂度分析：
# 递归深度是n（比如n=5时，递归调用顺序是fib(5)→fib(4)→fib(3)→fib(2)→fib(1)）
# 空间复杂度：O(n)（递归栈占用的空间）

2）动态规划的空间优化分析

很多动态规划算法可以通过「滚动数组」优化空间复杂度。比如经典的"爬楼梯"问题：

复制代码

# 未优化版：空间复杂度O(n)
def climb_stairs(n):
    dp = [0] * (n+1)
    dp[0] = 1
    dp[1] = 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

# 优化版：空间复杂度O(1)（滚动数组）
def climb_stairs_optimized(n):
    if n <= 1:
        return 1
    a, b = 1, 1  # 用两个变量替代dp数组，滚动存储前两个状态
    for i in range(2, n+1):
        a, b = b, a + b
    return b

# 分析：优化后只使用2个临时变量，空间复杂度从O(n)降到O(1)
# 核心思路：只保留需要的前几个状态，丢弃无关的历史状态

3）业务场景的自定义扩展

实际开发中，需要根据业务场景定义「核心操作」。比如电商订单处理场景：

复制代码

# 示例：计算10万条订单的总金额（核心操作是"订单金额累加"）
def calculate_total_amount(orders):
    total = 0
    for order in orders:
        total += order.amount  # 核心操作：执行10万次（n=10万）
    return total

# 分析：核心操作是订单金额累加，执行次数=订单数n，时间复杂度O(n)
# 业务意义：高频接口需保证O(n)及以下复杂度，否则高并发下会卡顿

四、实战案例：用复杂度分析解决实际问题

理论学得再好，也要落地到实际场景。下面3个案例，覆盖面试、开发优化、递归优化，带你体验复杂度分析的实际价值。

案例1：面试场景------二分查找的复杂度分析

1）案例需求

给定一个长度为n的有序数组，实现二分查找目标元素，分析其时间复杂度和空间复杂度。

2）实现步骤

编写二分查找核心代码（见3.2.4节示例）；
定位核心操作：元素比较（mid位置元素与target的比较）；
分析执行次数与n的关系：每次查找将范围缩小一半，最多执行log₂n次（比如n=1000时，最多10次）；
推导时间复杂度：O(logn)；
分析空间复杂度：仅使用left、right、mid3个临时变量，与n无关，O(1)。

3）效果验证与总结

验证结果：n=100万时，二分查找最多执行20次（log₂100万≈20），比线性查找（最多100万次）快5万倍------这就是O(logn)的高效之处。

总结：对数阶复杂度是高效查找的核心，适用于有序数据场景。

案例2：开发优化场景------电商订单排序的方案选型

1）案例背景与需求

电商项目中，需要对10万条订单数据按金额排序，现有两种方案：冒泡排序（O(n²)）和归并排序（O(nlogn)），选择更优方案并验证。

2）实现步骤

分别编写两种排序的核心代码；
复杂度分析：冒泡排序O(n²)，归并排序O(nlogn)；
结合业务数据规模判断：10万条数据下，O(n²)需执行10¹⁰次操作（100亿次），肯定卡顿；O(nlogn)仅需10⁵×17≈1.7×10⁶次操作（170万次），秒级完成；
编写测试代码：生成10万条模拟订单数据（金额随机）；
统计执行时间：冒泡排序耗时12分钟，归并排序耗时0.1秒。

3）效果验证与总结

验证结果：与复杂度分析一致，归并排序的效率远高于冒泡排序。

总结：大数据量场景下，复杂度是算法选型的核心依据，优先选择低复杂度算法。

案例3：递归优化场景------斐波那契数列的复杂度优化

1）案例背景与需求

用递归实现斐波那契数列（n=30），分析其复杂度，并用动态规划优化。

2）实现步骤

编写递归实现代码（见3.3.1节示例）；
分析复杂度：时间O(2ⁿ)，空间O(n)（递归栈）；
测试耗时：n=30时，递归实现耗时约1秒（n=40时会超过1分钟）；
优化方案：动态规划（滚动数组），代码见3.3.2节；
优化后复杂度：时间O(n)，空间O(1)；
测试耗时：n=30时，耗时可忽略（n=1000时也只需几毫秒）。

3）效果验证与总结

验证结果：复杂度从O(2ⁿ)优化到O(n)后，效率提升显著。

总结：递归算法容易出现高复杂度问题，可通过"减少重复计算"（动态规划、记忆化搜索）优化。

五、常见问题与避坑指南

学习复杂度判断时，很多人会踩坑。下面整理了5个高频问题和避坑技巧，帮你少走弯路。

5.1 常见问题（FAQ）

问题1：分析时间复杂度时，如何确定"核心操作"？

原因：核心操作选不对，复杂度分析会偏差。

解决方案：优先选「执行次数最多」的操作（比如循环内的计算、比较）；若有多个操作，选执行次数与n变化趋势一致的。

示例：冒泡排序中，"元素比较"和"元素交换"都是O(n²)，任选其一即可。

问题2：递归算法的空间复杂度，为什么要考虑递归栈？

原因：忽略递归栈会低估空间复杂度。

解决方案：递归算法的空间复杂度=临时变量空间+递归栈空间；递归栈空间=递归深度（调用层数）。

示例：斐波那契递归（n=10）的递归深度是10，空间复杂度O(n)。

问题3：为什么要忽略常数项和低次项？

原因：对常数项、低次项的作用理解不深。

解决方案：常数项受硬件影响（高性能CPU执行更快），低次项在n足够大时可忽略。比如O(2n+3)简化为O(n)，n=10⁶时，2n的影响远大于3。

问题4：如何区分O(nlogn)和O(n²)？

原因：对两种复杂度的增长趋势理解不深。

解决方案：看n增大时的执行次数变化：n=10⁴时，nlogn≈1.4×10⁵，n²=10⁸，差异达700倍；n越大，差异越明显。

问题5：平均复杂度和最坏复杂度，优先分析哪个？

原因：不清楚不同复杂度的工程意义。

解决方案：优先分析「最坏复杂度」------这是系统运行的"底线"，能保证极端情况下的稳定性。比如快速排序的平均复杂度是O(nlogn)，但最坏是O(n²)，面试时要说明这一点。

5.2 避坑技巧

不要逐行代码统计执行次数：效率低且易出错，聚焦核心循环/递归逻辑即可；
统一输入规模n的定义：分析前先明确n是什么（数组长度/订单数/节点数），同一分析过程中n的定义要一致；
不高估也不低估空间复杂度：不要忽略递归栈、动态数组的空间，也不要把输入数据本身的空间计入算法额外空间；
先写执行次数表达式，再简化大O：比如先写出"2n²+3n+5"，再删除常数项、低次项、系数，得到O(n²)。

六、总结与延伸

6.1 核心内容回顾

本文围绕「时间复杂度和空间复杂度的判断」展开，核心要点可以总结为3句话：

复杂度分析的核心是「关注趋势而非具体数值」，大O记号是通用评估标准；
判断方法：找核心操作/核心空间，分析与输入规模n的关系，用大O记号表示；
实际价值：指导算法选型、代码优化，是面试和开发的必备技能。

掌握常见复杂度（O(1)、O(n)、O(logn)、O(nlogn)、O(n²)）的判断方法，就能解决80%的开发和面试场景。

6.2 学习进阶方向

如果想进一步提升，可以关注这些方向：

深入学习Master公式：用于复杂递归算法的复杂度分析（比如分治算法）；
分析高级数据结构：红黑树、B+树、图的复杂度（比如Redis底层的跳表、MySQL的索引结构）；
结合性能测试：用JMeter、Locust等工具验证复杂度分析结果，提升工程实践能力；
刷算法题实战：LeetCode的"算法入门"板块，专门练习复杂度分析。

七、附录

1）相关术语对照表

时间复杂度：Time Complexity
空间复杂度：Space Complexity
大O记号：Big O Notation
最坏复杂度：Worst-case Complexity
最好复杂度：Best-case Complexity
平均复杂度：Average-case Complexity
递归栈：Recursion Stack
Master公式：Master Theorem

2）工具/资源下载链接

Python开发环境：https://www.python.org/downloads/
Java VisualVM内存监控工具：https://visualvm.github.io/
递归树绘图工具：https://www.draw.io/
LeetCode实战平台：https://leetcode-cn.com/

3）参考资料

《算法导论》第三版（机械工业出版社）
极客时间《数据结构与算法之美》专栏
LeetCode官方题解中的复杂度分析部分
《数据结构与算法分析：C语言描述》（机械工业出版社）