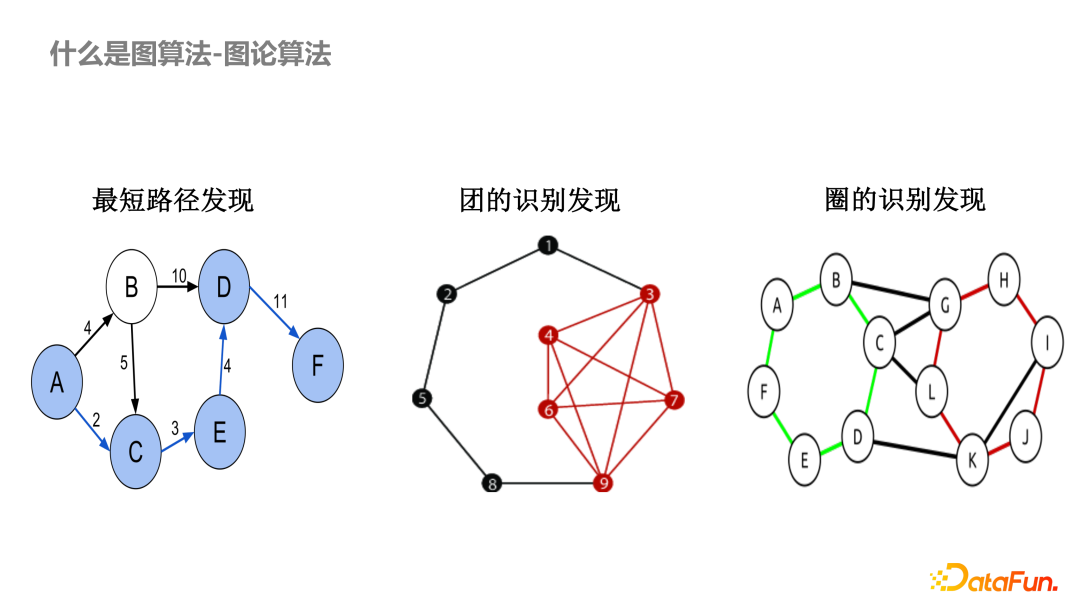
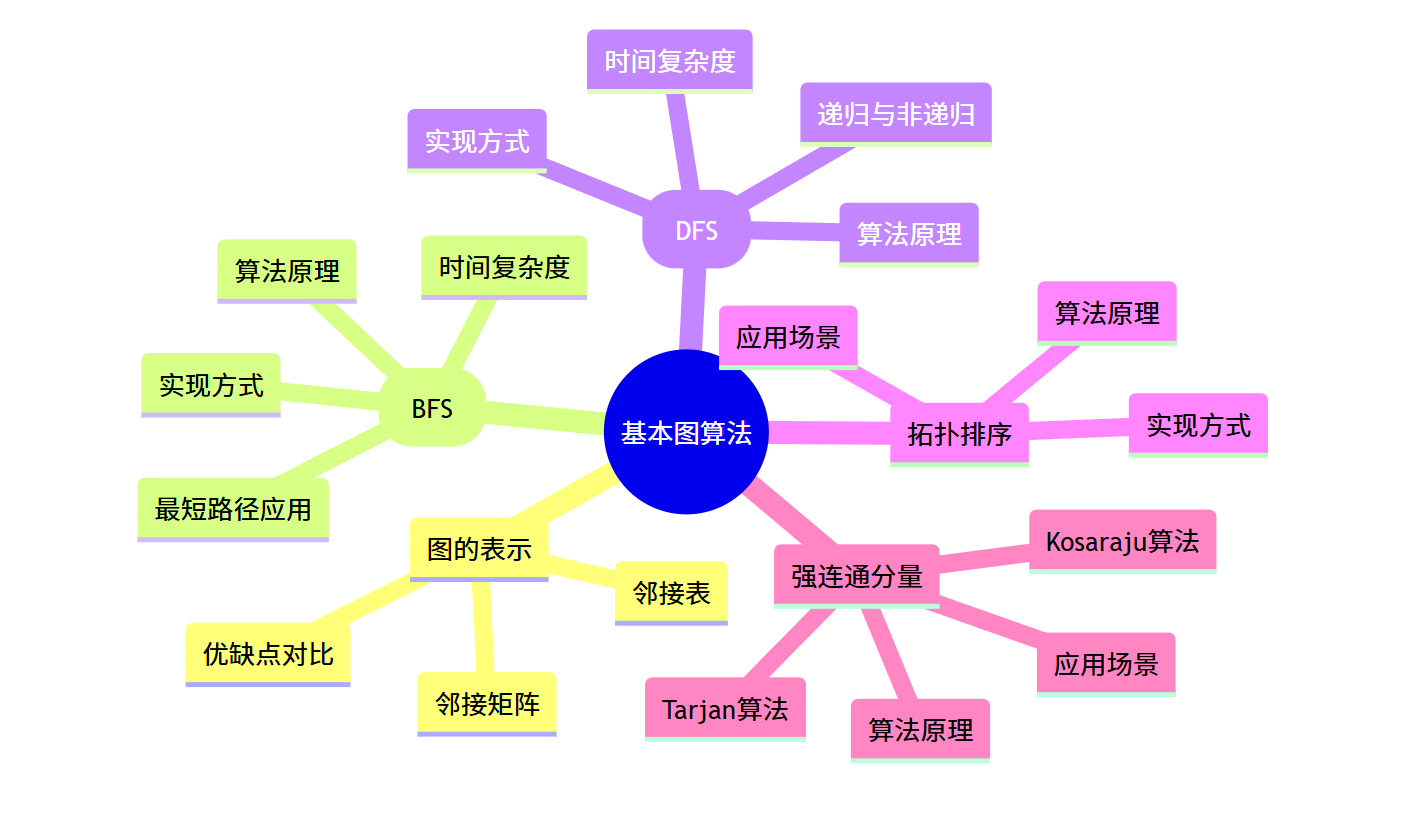
大家好!今天我们来深入学习《算法导论》第 22 章的基本图算法。图论是计算机科学中的重要基础,这些基本算法是解决很多复杂问题的基石。本文将结合代码实现,帮助大家更好地理解和应用这些算法。
思维导图
22.1 图的表示
在计算机中,图有两种主要的表示方式:邻接表和邻接矩阵。
邻接表
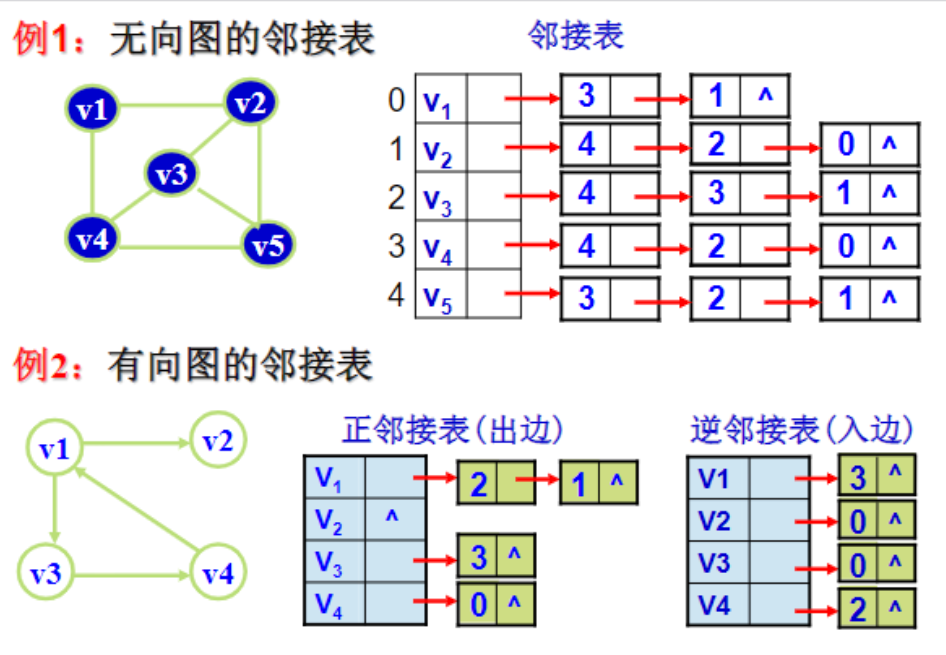
邻接表由一个包含所有顶点的数组和每个顶点对应的链表(或动态数组)组成,链表中存储了与该顶点相邻的所有顶点。
邻接矩阵
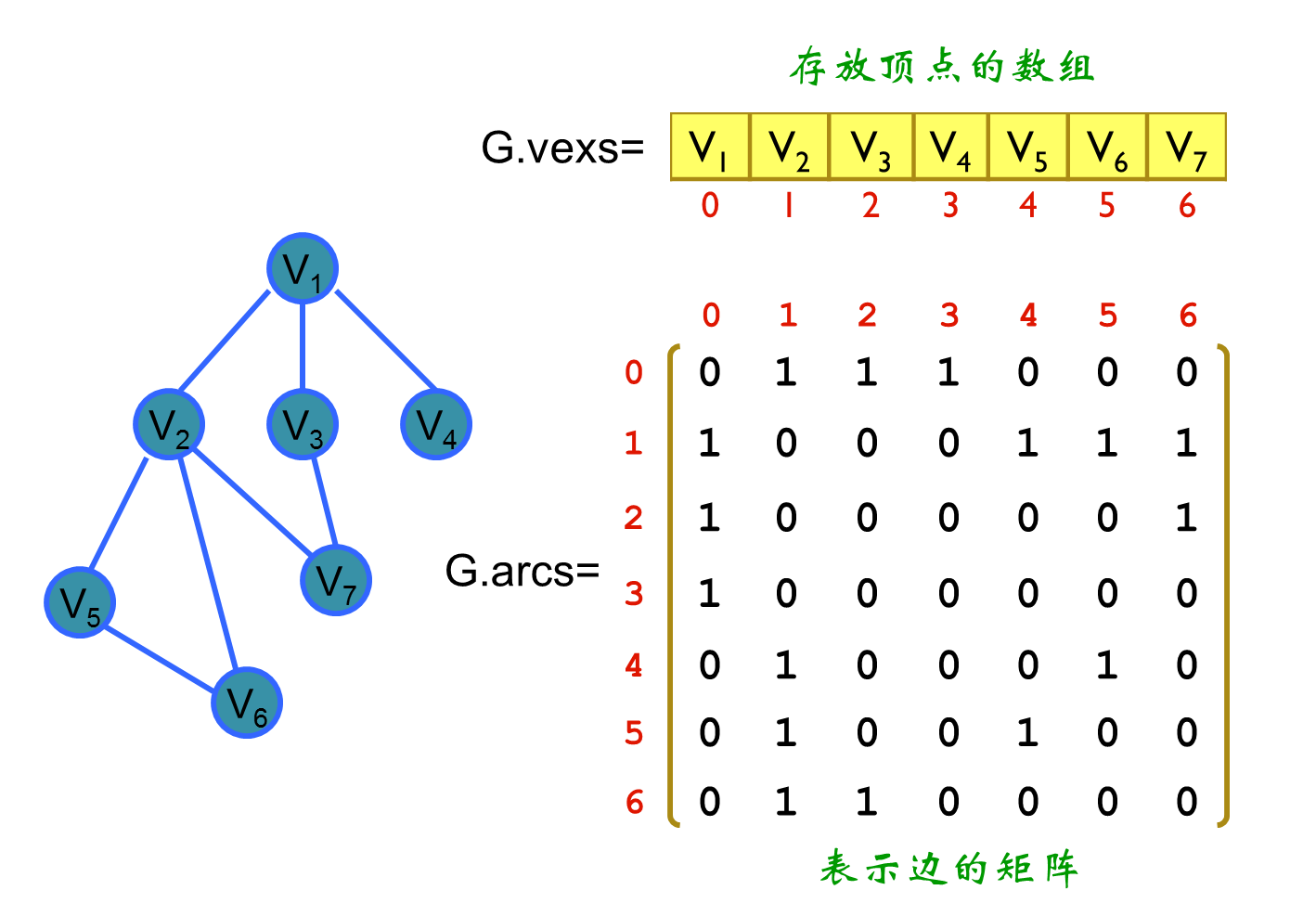
邻接矩阵是一个二维数组,当有边从顶点 i 指向顶点 j 时,矩阵中的元素 matrix [i][j] 为 1(或边的权重),否则为 0。
两种表示方式的对比
| 操作 | 邻接表 | 邻接矩阵 |
|---|---|---|
| 存储空间 | O(V+E) | O(V²) |
| 检查 (u,v) 是否为边 | O(degree(u)) | O(1) |
| 找出 u 的所有邻接顶点 | O(degree(u)) | O(V) |
| 添加边 | O(1) | O(1) |
| 删除边 | O(degree(u)) | O(1) |
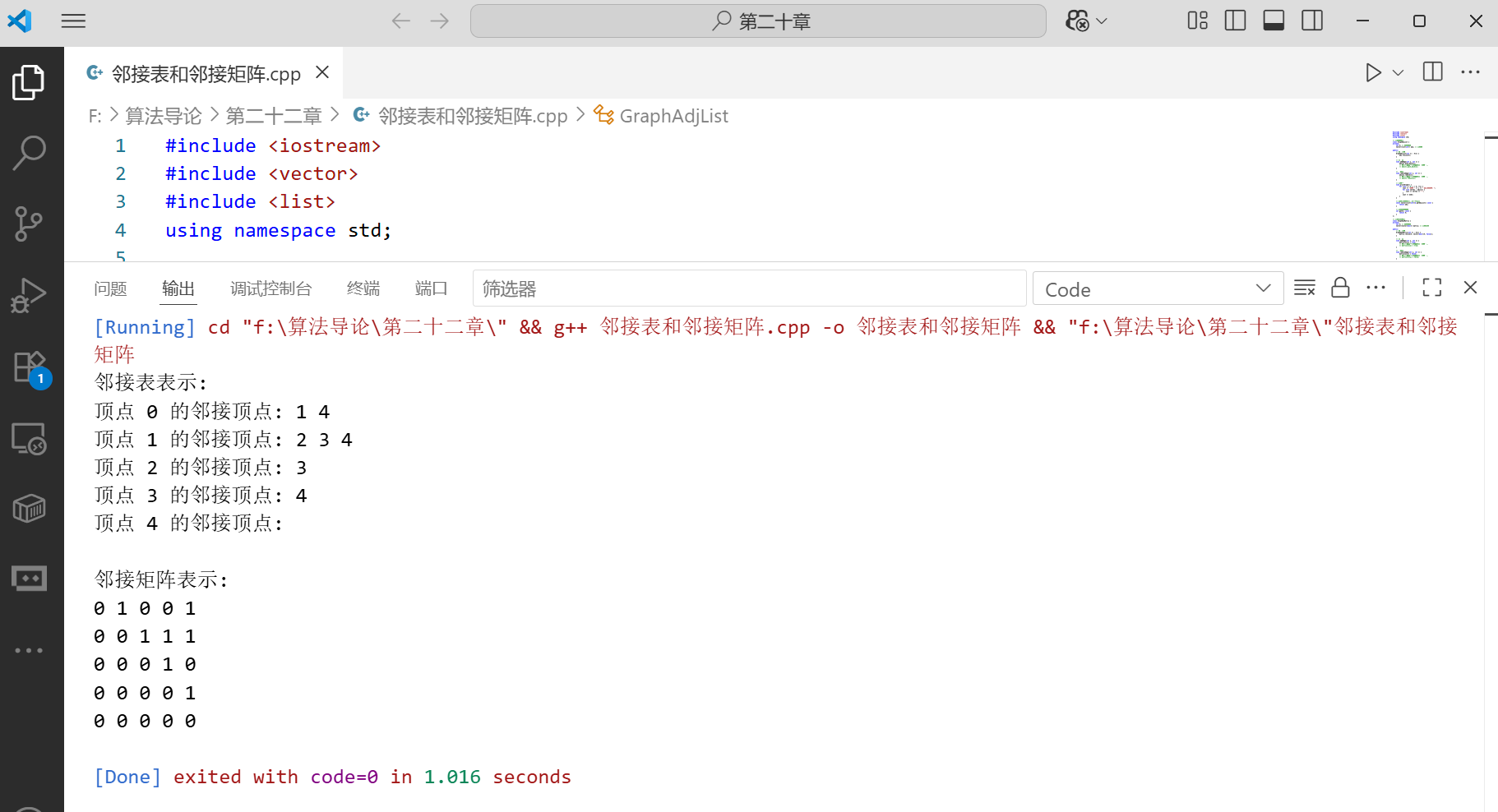
图的表示代码实现
下面是 C++ 中实现图的邻接表和邻接矩阵表示的代码:
#include <iostream>
#include <vector>
#include <list>
using namespace std;
// 邻接表表示
class GraphAdjList {
private:
int V; // 顶点数量
vector<list<int>> adj; // 邻接表
public:
// 构造函数
GraphAdjList(int v) : V(v) {
adj.resize(V);
}
// 添加边
void addEdge(int u, int v) {
adj[u].push_back(v);
// 如果是无向图,还需要添加下面一行
// adj[v].push_back(u);
}
// 删除边
void removeEdge(int u, int v) {
adj[u].remove(v);
// 如果是无向图,还需要添加下面一行
// adj[v].remove(u);
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
cout << "顶点 " << i << " 的邻接顶点: ";
for (int vertex : adj[i]) {
cout << vertex << " ";
}
cout << endl;
}
}
// 获取邻接表(用于后续算法)
const vector<list<int>>& getAdjList() const {
return adj;
}
// 获取顶点数量
int getV() const {
return V;
}
};
// 邻接矩阵表示
class GraphAdjMatrix {
private:
int V; // 顶点数量
vector<vector<bool>> matrix; // 邻接矩阵
public:
// 构造函数
GraphAdjMatrix(int v) : V(v) {
matrix.resize(V, vector<bool>(V, false));
}
// 添加边
void addEdge(int u, int v) {
matrix[u][v] = true;
// 如果是无向图,还需要添加下面一行
// matrix[v][u] = true;
}
// 删除边
void removeEdge(int u, int v) {
matrix[u][v] = false;
// 如果是无向图,还需要添加下面一行
// matrix[v][u] = false;
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
}
// 获取邻接矩阵(用于后续算法)
const vector<vector<bool>>& getAdjMatrix() const {
return matrix;
}
// 获取顶点数量
int getV() const {
return V;
}
};
// 测试代码
int main() {
// 测试邻接表
cout << "邻接表表示:" << endl;
GraphAdjList g1(5);
g1.addEdge(0, 1);
g1.addEdge(0, 4);
g1.addEdge(1, 2);
g1.addEdge(1, 3);
g1.addEdge(1, 4);
g1.addEdge(2, 3);
g1.addEdge(3, 4);
g1.printGraph();
// 测试邻接矩阵
cout << "\n邻接矩阵表示:" << endl;
GraphAdjMatrix g2(5);
g2.addEdge(0, 1);
g2.addEdge(0, 4);
g2.addEdge(1, 2);
g2.addEdge(1, 3);
g2.addEdge(1, 4);
g2.addEdge(2, 3);
g2.addEdge(3, 4);
g2.printGraph();
return 0;
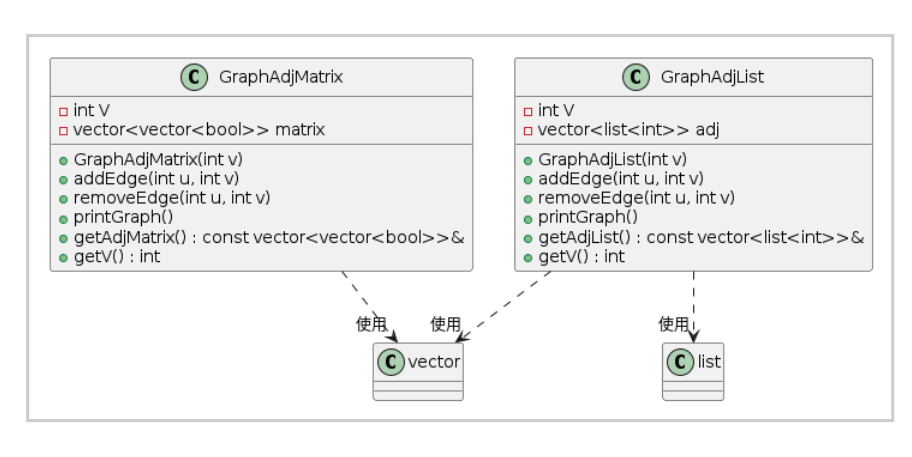
}图表示类图
@startuml
class GraphAdjList {
- int V
- vector<list<int>> adj
+ GraphAdjList(int v)
+ addEdge(int u, int v)
+ removeEdge(int u, int v)
+ printGraph()
+ getAdjList() : const vector<list<int>>&
+ getV() : int
}
class GraphAdjMatrix {
- int V
- vector<vector<bool>> matrix
+ GraphAdjMatrix(int v)
+ addEdge(int u, int v)
+ removeEdge(int u, int v)
+ printGraph()
+ getAdjMatrix() : const vector<vector<bool>>&
+ getV() : int
}
GraphAdjList ..> "使用" vector
GraphAdjList ..> "使用" list
GraphAdjMatrix ..> "使用" vector
@enduml22.2 广度优先搜索
广度优先搜索(BFS)是一种图遍历算法,它从起始顶点开始,先访问起始顶点的所有邻接顶点,然后再依次访问这些邻接顶点的邻接顶点,以此类推。
BFS 算法流程图
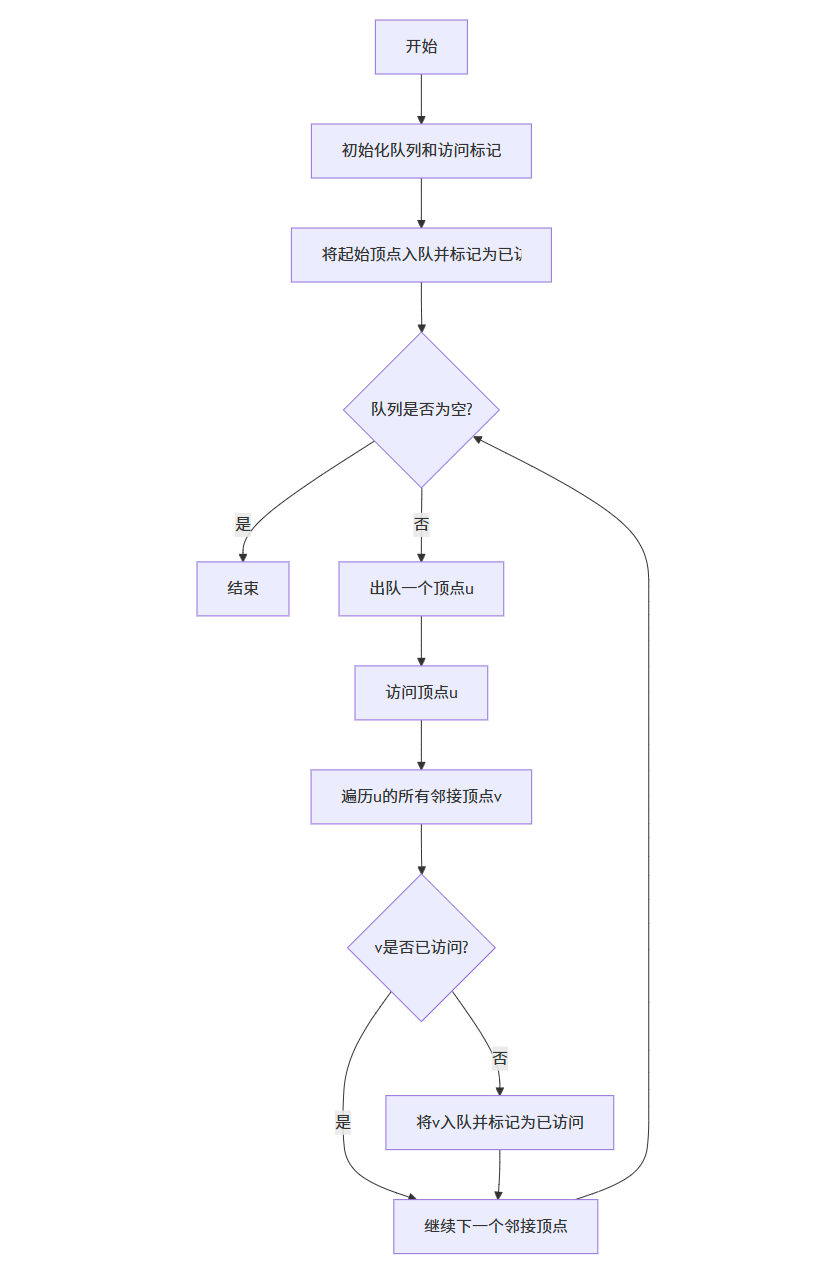
BFS 算法实现
下面是使用邻接表实现 BFS 的代码:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
using namespace std;
// 使用前面定义的GraphAdjList类
class GraphAdjList {
private:
int V; // 顶点数量
vector<list<int>> adj; // 邻接表
public:
// 构造函数
GraphAdjList(int v) : V(v) {
adj.resize(V);
}
// 添加边
void addEdge(int u, int v) {
adj[u].push_back(v);
// 如果是无向图,还需要添加下面一行
// adj[v].push_back(u);
}
// 删除边
void removeEdge(int u, int v) {
adj[u].remove(v);
// 如果是无向图,还需要添加下面一行
// adj[v].remove(u);
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
cout << "顶点 " << i << " 的邻接顶点: ";
for (int vertex : adj[i]) {
cout << vertex << " ";
}
cout << endl;
}
}
// 获取邻接表(用于后续算法)
const vector<list<int>>& getAdjList() const {
return adj;
}
// 获取顶点数量
int getV() const {
return V;
}
// BFS遍历
void BFS(int start) {
// 标记顶点是否被访问
vector<bool> visited(V, false);
// 创建队列
queue<int> q;
// 标记起始顶点为已访问并入队
visited[start] = true;
q.push(start);
cout << "BFS遍历结果: ";
while (!q.empty()) {
// 出队一个顶点
int u = q.front();
q.pop();
// 访问顶点
cout << u << " ";
// 遍历所有邻接顶点
for (int v : adj[u]) {
if (!visited[v]) {
visited[v] = true;
q.push(v);
}
}
}
cout << endl;
}
// BFS应用:计算从start到其他所有顶点的最短路径
vector<int> shortestPathBFS(int start) {
vector<int> distance(V, -1); // -1表示不可达
queue<int> q;
distance[start] = 0;
q.push(start);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v : adj[u]) {
if (distance[v] == -1) {
distance[v] = distance[u] + 1;
q.push(v);
}
}
}
return distance;
}
};
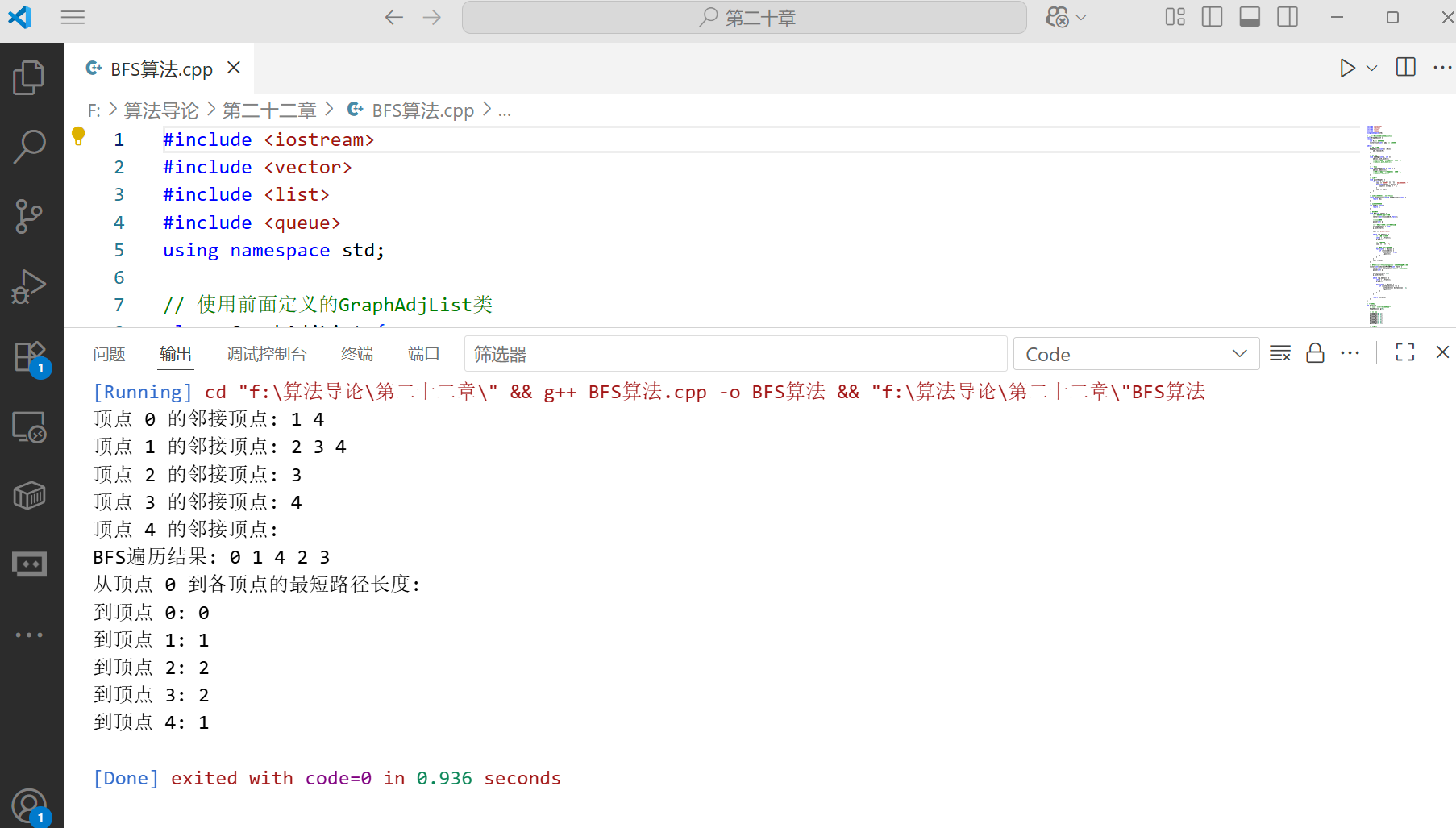
// 测试代码
int main() {
// 创建一个包含5个顶点的图
GraphAdjList g(5);
// 添加边
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
// 打印图
g.printGraph();
// BFS遍历
int start = 0;
g.BFS(start);
// 计算最短路径
vector<int> distances = g.shortestPathBFS(start);
cout << "从顶点 " << start << " 到各顶点的最短路径长度: " << endl;
for (int i = 0; i < distances.size(); ++i) {
cout << "到顶点 " << i << ": " << distances[i] << endl;
}
return 0;
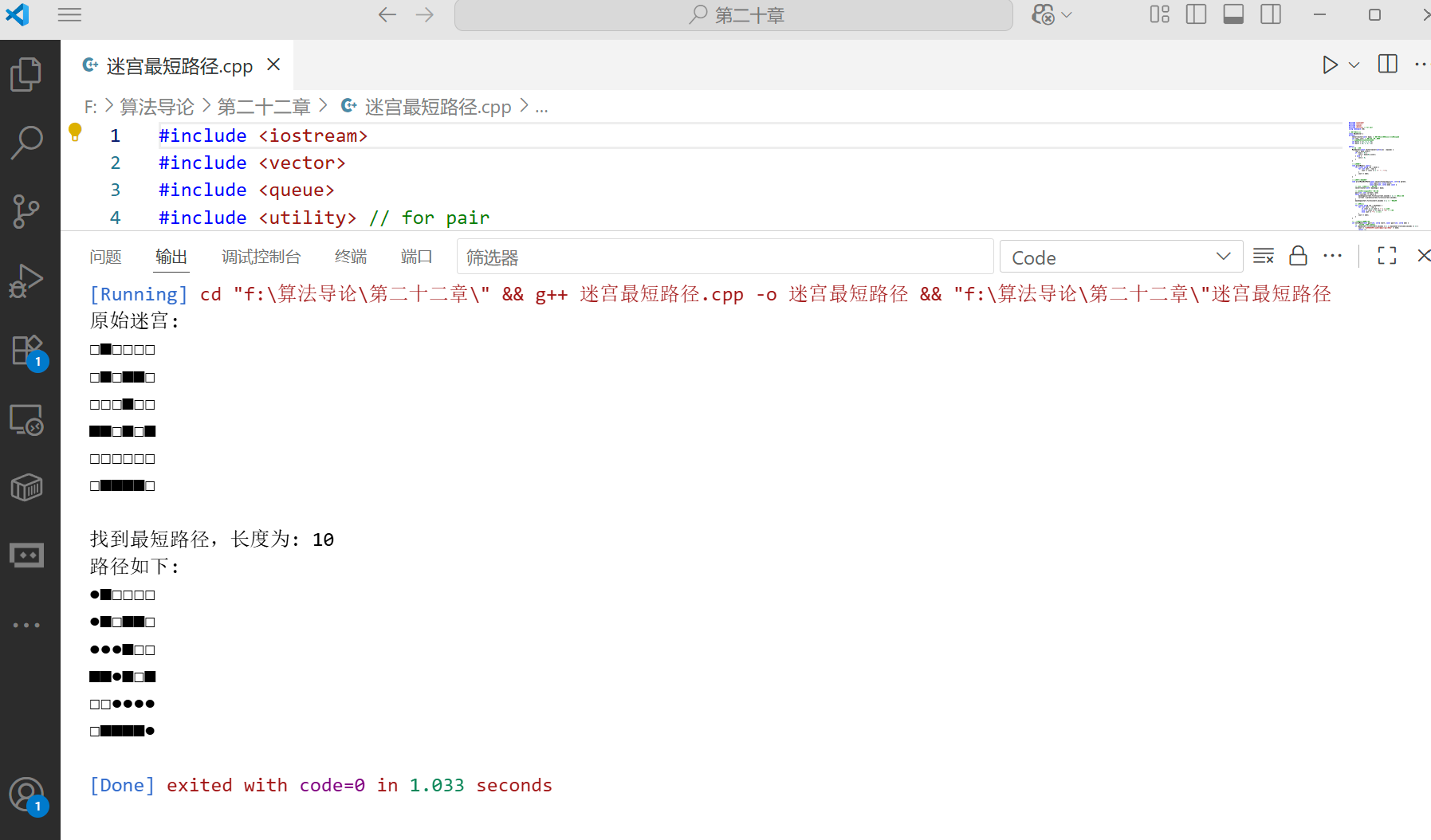
}BFS 算法综合应用:迷宫最短路径
下面是一个使用 BFS 算法求解迷宫最短路径的完整示例:
#include <iostream>
#include <vector>
#include <queue>
#include <utility> // for pair
using namespace std;
// 迷宫求解器类
class MazeSolver {
private:
vector<vector<int>> maze; // 迷宫表示,0表示通路,1表示墙壁
int rows, cols; // 迷宫的行数和列数
// 方向数组:上、右、下、左
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
public:
// 构造函数
MazeSolver(const vector<vector<int>>& m) : maze(m) {
rows = maze.size();
if (rows > 0) {
cols = maze[0].size();
} else {
cols = 0;
}
}
// 打印迷宫
void printMaze() const {
for (const auto& row : maze) {
for (int cell : row) {
cout << (cell == 1 ? "■" : "□");
}
cout << endl;
}
}
// 打印带路径的迷宫
void printMazeWithPath(const vector<vector<pair<int, int>>>& parent,
const pair<int, int>& start,
const pair<int, int>& end) const {
// 创建一个副本用于标记路径
vector<vector<int>> mazeCopy = maze;
// 从终点回溯到起点,标记路径
pair<int, int> current = end;
while (current != start) {
mazeCopy[current.first][current.second] = 2; // 2表示路径
current = parent[current.first][current.second];
}
mazeCopy[start.first][start.second] = 2; // 标记起点
// 打印结果
for (const auto& row : mazeCopy) {
for (int cell : row) {
if (cell == 1) cout << "■"; // 墙壁
else if (cell == 2) cout << "●"; // 路径
else cout << "□"; // 通路
}
cout << endl;
}
}
// 使用BFS寻找最短路径
int solveMaze(const pair<int, int>& start, const pair<int, int>& end) {
// 检查起点和终点是否合法
if (maze[start.first][start.second] == 1 || maze[end.first][end.second] == 1) {
cout << "起点或终点是墙壁,无法找到路径!" << endl;
return -1;
}
// 检查是否已经在终点
if (start == end) {
cout << "起点就是终点!" << endl;
return 0;
}
// 记录是否访问过
vector<vector<bool>> visited(rows, vector<bool>(cols, false));
// 记录每个位置的前一个位置,用于回溯路径
vector<vector<pair<int, int>>> parent(rows, vector<pair<int, int>>(cols, {-1, -1}));
// BFS队列,存储位置和距离
queue<pair<pair<int, int>, int>> q;
// 初始化起点
q.push({start, 0});
visited[start.first][start.second] = true;
// BFS遍历
while (!q.empty()) {
auto current = q.front();
q.pop();
pair<int, int> pos = current.first;
int distance = current.second;
// 检查是否到达终点
if (pos == end) {
cout << "找到最短路径,长度为: " << distance << endl;
cout << "路径如下:" << endl;
printMazeWithPath(parent, start, end);
return distance;
}
// 探索四个方向
for (int i = 0; i < 4; ++i) {
int newRow = pos.first + dx[i];
int newCol = pos.second + dy[i];
// 检查新位置是否合法且未被访问
if (newRow >= 0 && newRow < rows && newCol >= 0 && newCol < cols &&
maze[newRow][newCol] == 0 && !visited[newRow][newCol]) {
visited[newRow][newCol] = true;
parent[newRow][newCol] = pos;
q.push({{newRow, newCol}, distance + 1});
}
}
}
// 如果队列为空仍未找到终点,则无解
cout << "没有找到从起点到终点的路径!" << endl;
return -1;
}
};
// 测试代码
int main() {
// 定义一个迷宫,0表示通路,1表示墙壁
vector<vector<int>> maze = {
{0, 1, 0, 0, 0, 0},
{0, 1, 0, 1, 1, 0},
{0, 0, 0, 1, 0, 0},
{1, 1, 0, 1, 0, 1},
{0, 0, 0, 0, 0, 0},
{0, 1, 1, 1, 1, 0}
};
// 创建迷宫求解器
MazeSolver solver(maze);
// 打印原始迷宫
cout << "原始迷宫:" << endl;
solver.printMaze();
cout << endl;
// 定义起点和终点
pair<int, int> start = {0, 0};
pair<int, int> end = {5, 5};
// 求解迷宫
solver.solveMaze(start, end);
return 0;
}22.3 深度优先搜索
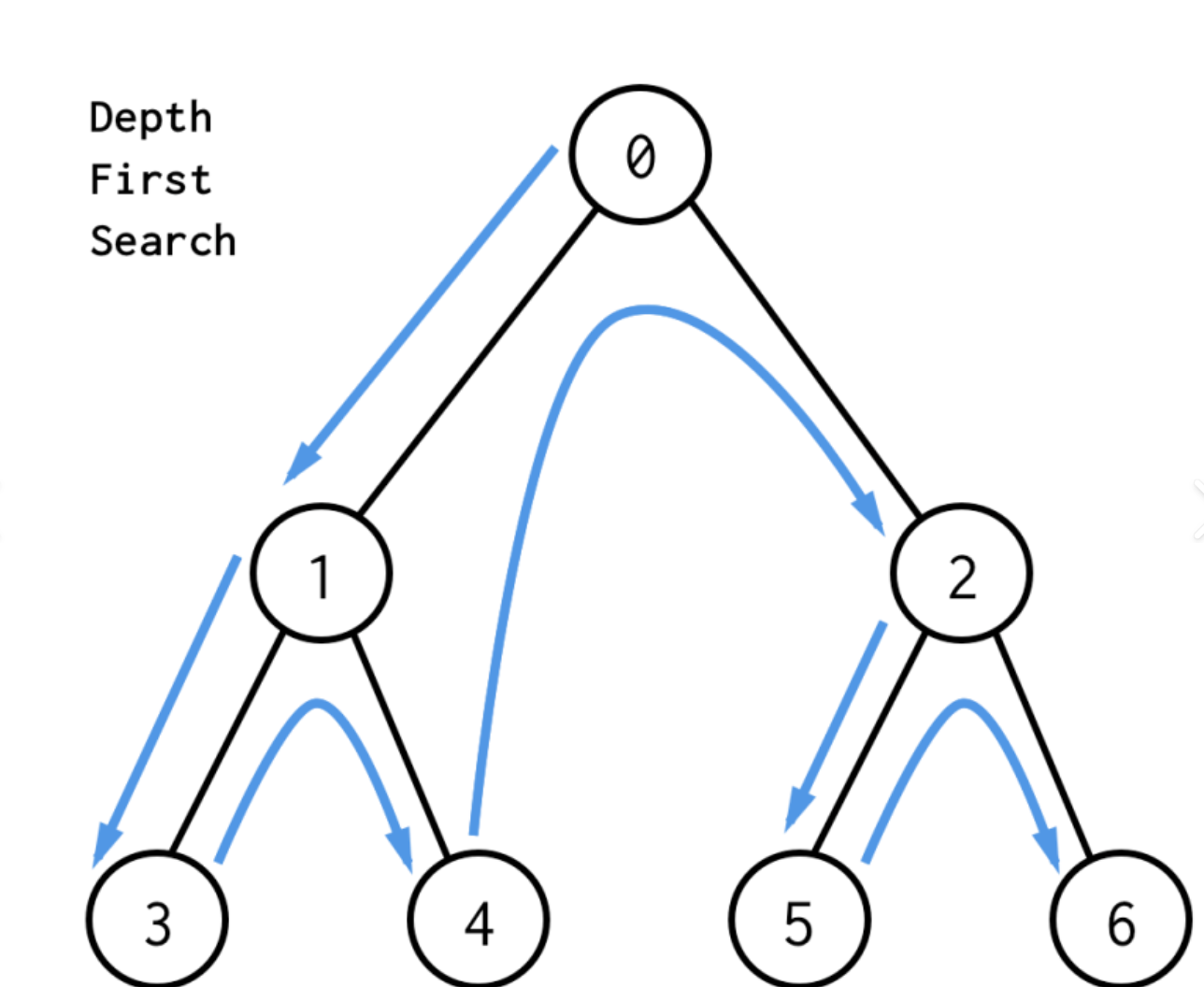
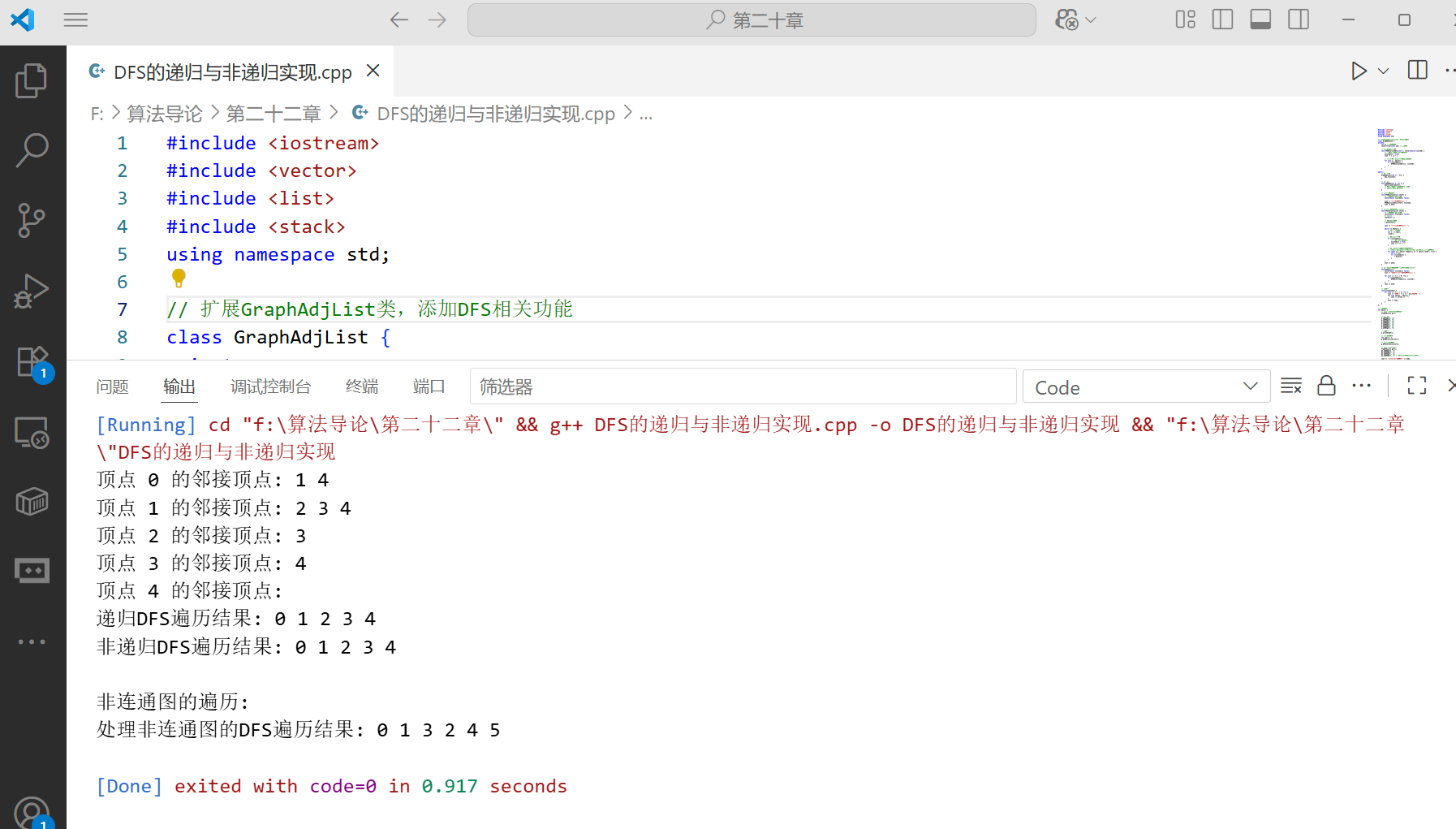
深度优先搜索(DFS)是另一种重要的图遍历算法。它从起始顶点开始,尽可能深地搜索图的分支,当无法继续前进时,回溯到上一个未探索完毕的顶点,继续搜索其他分支。
DFS 算法实现
下面是 DFS 的递归和非递归实现代码:
#include <iostream>
#include <vector>
#include <list>
#include <stack>
using namespace std;
// 扩展GraphAdjList类,添加DFS相关功能
class GraphAdjList {
private:
int V; // 顶点数量
vector<list<int>> adj; // 邻接表
// 递归DFS辅助函数
void DFSRecursiveUtil(int v, vector<bool>& visited) {
// 标记当前顶点为已访问并输出
visited[v] = true;
cout << v << " ";
// 递归访问所有未被访问的邻接顶点
for (int u : adj[v]) {
if (!visited[u]) {
DFSRecursiveUtil(u, visited);
}
}
}
public:
// 构造函数
GraphAdjList(int v) : V(v) {
adj.resize(V);
}
// 添加边
void addEdge(int u, int v) {
adj[u].push_back(v);
// 如果是无向图,还需要添加下面一行
// adj[v].push_back(u);
}
// 递归实现的DFS
void DFSRecursive(int start) {
// 标记顶点是否被访问
vector<bool> visited(V, false);
cout << "递归DFS遍历结果: ";
DFSRecursiveUtil(start, visited);
cout << endl;
}
// 非递归实现的DFS(使用栈)
void DFSIterative(int start) {
// 标记顶点是否被访问
vector<bool> visited(V, false);
// 创建栈
stack<int> s;
// 压入起始顶点
s.push(start);
cout << "非递归DFS遍历结果: ";
while (!s.empty()) {
// 弹出一个顶点
int v = s.top();
s.pop();
// 如果未被访问
if (!visited[v]) {
// 标记为已访问并输出
visited[v] = true;
cout << v << " ";
}
// 将所有未被访问的邻接顶点入栈
// 注意:为了保持与递归版本相同的顺序,这里使用反向迭代器
for (auto it = adj[v].rbegin(); it != adj[v].rend(); ++it) {
int u = *it;
if (!visited[u]) {
s.push(u);
}
}
}
cout << endl;
}
// 对所有未访问的顶点执行DFS,处理非连通图
void DFSFull() {
vector<bool> visited(V, false);
cout << "处理非连通图的DFS遍历结果: ";
for (int i = 0; i < V; ++i) {
if (!visited[i]) {
DFSRecursiveUtil(i, visited);
}
}
cout << endl;
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
cout << "顶点 " << i << " 的邻接顶点: ";
for (int vertex : adj[i]) {
cout << vertex << " ";
}
cout << endl;
}
}
};
// 测试代码
int main() {
// 创建一个包含5个顶点的图
GraphAdjList g(5);
// 添加边
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
// 打印图
g.printGraph();
// 递归DFS遍历
int start = 0;
g.DFSRecursive(start);
// 非递归DFS遍历
g.DFSIterative(start);
// 创建一个非连通图
GraphAdjList g2(6);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(1, 3);
g2.addEdge(4, 5); // 这个连通分量与其他部分分离
cout << "\n非连通图的遍历:" << endl;
g2.DFSFull();
return 0;
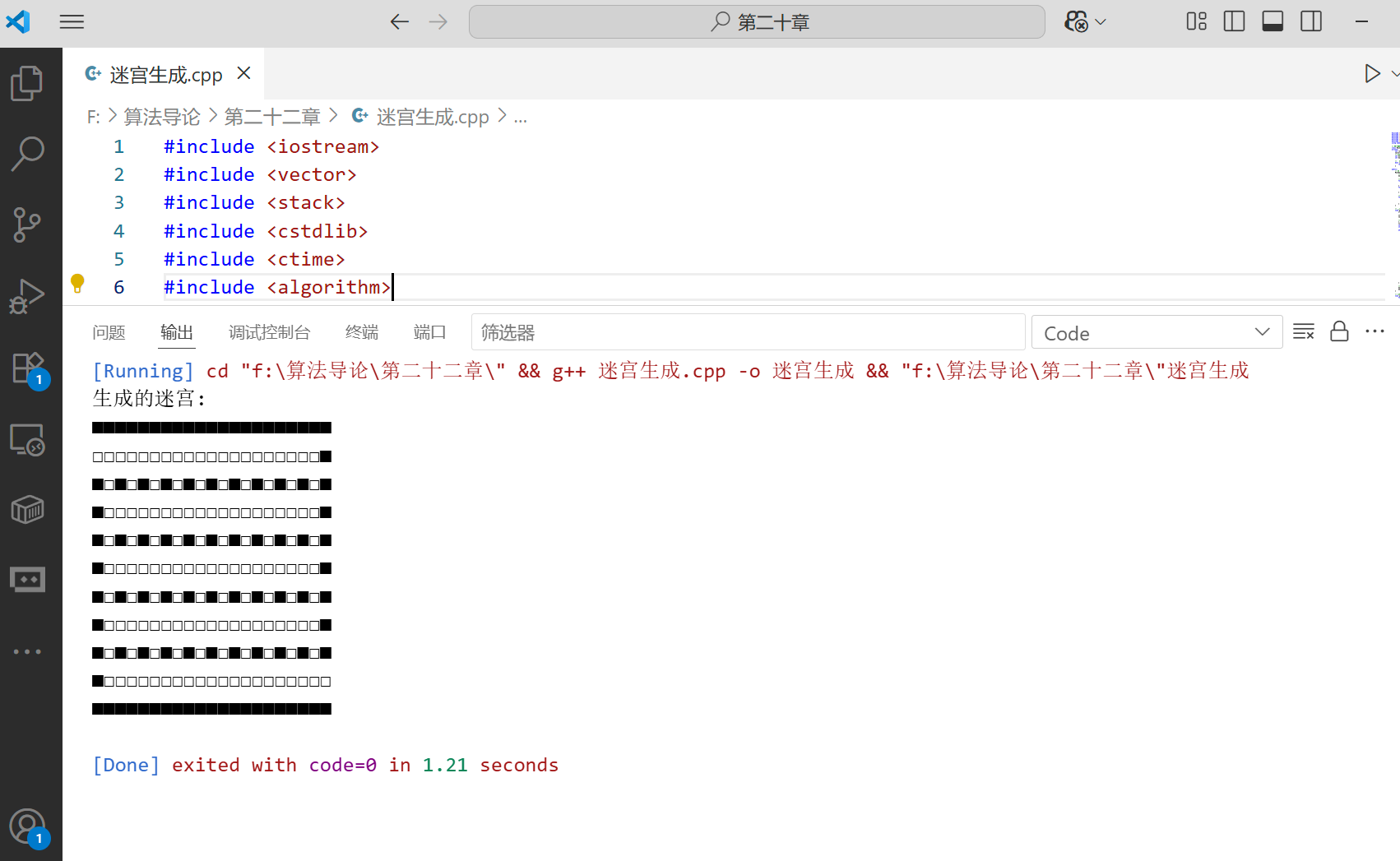
}DFS 算法综合应用:迷宫生成
DFS 可以用于随机生成迷宫,基本思路是从一个起点开始,随机选择一个方向前进,遇到未访问的单元格就打通墙壁并继续,直到无路可走时回溯,直到所有单元格都被访问。
#include <iostream>
#include <vector>
#include <stack>
#include <cstdlib>
#include <ctime>
#include <algorithm>
using namespace std;
// 迷宫生成器类
class MazeGenerator {
private:
int rows, cols; // 迷宫的行数和列数(建议使用奇数)
vector<vector<int>> maze; // 迷宫表示,0表示通路,1表示墙壁
// 方向数组:上、右、下、左
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
// 检查位置是否合法且未被访问
bool isLegal(int x, int y) {
return x > 0 && x < rows && y > 0 && y < cols && maze[x][y] == 0;
}
public:
// 构造函数
MazeGenerator(int r, int c) : rows(r), cols(c) {
// 初始化迷宫,全部设为通路
maze.resize(rows, vector<int>(cols, 0));
// 构建外围墙壁
for (int i = 0; i < rows; ++i) {
maze[i][0] = 1;
maze[i][cols-1] = 1;
}
for (int j = 0; j < cols; ++j) {
maze[0][j] = 1;
maze[rows-1][j] = 1;
}
// 构建内部墙壁(仅对奇数行和奇数列)
for (int i = 2; i < rows-1; i += 2) {
for (int j = 2; j < cols-1; j += 2) {
maze[i][j] = 1;
}
}
}
// 使用DFS生成迷宫
void generateMaze(int startX = 1, int startY = 1) {
srand(time(0)); // 初始化随机数生成器
stack<pair<int, int>> s;
vector<vector<bool>> visited(rows, vector<bool>(cols, false));
// 从起点开始
s.push({startX, startY});
visited[startX][startY] = true;
int visitedCount = 1;
int totalCells = ((rows - 1) / 2) * ((cols - 1) / 2);
while (visitedCount < totalCells) {
auto current = s.top();
int x = current.first;
int y = current.second;
// 收集所有可能的方向
vector<int> directions = {0, 1, 2, 3};
random_shuffle(directions.begin(), directions.end());
bool moved = false;
for (int dir : directions) {
int nx = x + 2 * dx[dir]; // 移动两步(跳过墙壁)
int ny = y + 2 * dy[dir];
if (isLegal(nx, ny) && !visited[nx][ny]) {
// 打通当前位置和新位置之间的墙壁
maze[x + dx[dir]][y + dy[dir]] = 0;
// 移动到新位置
visited[nx][ny] = true;
visitedCount++;
s.push({nx, ny});
moved = true;
break;
}
}
// 如果不能移动,回溯
if (!moved) {
s.pop();
}
}
// 设置入口和出口
maze[1][0] = 0; // 入口
maze[rows-2][cols-1] = 0; // 出口
}
// 打印迷宫
void printMaze() const {
for (const auto& row : maze) {
for (int cell : row) {
cout << (cell == 1 ? "■" : "□");
}
cout << endl;
}
}
};
// 测试代码
int main() {
// 创建一个11x21的迷宫(建议使用奇数)
MazeGenerator generator(11, 21);
// 生成迷宫
generator.generateMaze();
// 打印迷宫
cout << "生成的迷宫:" << endl;
generator.printMaze();
return 0;
}22.4 拓扑排序
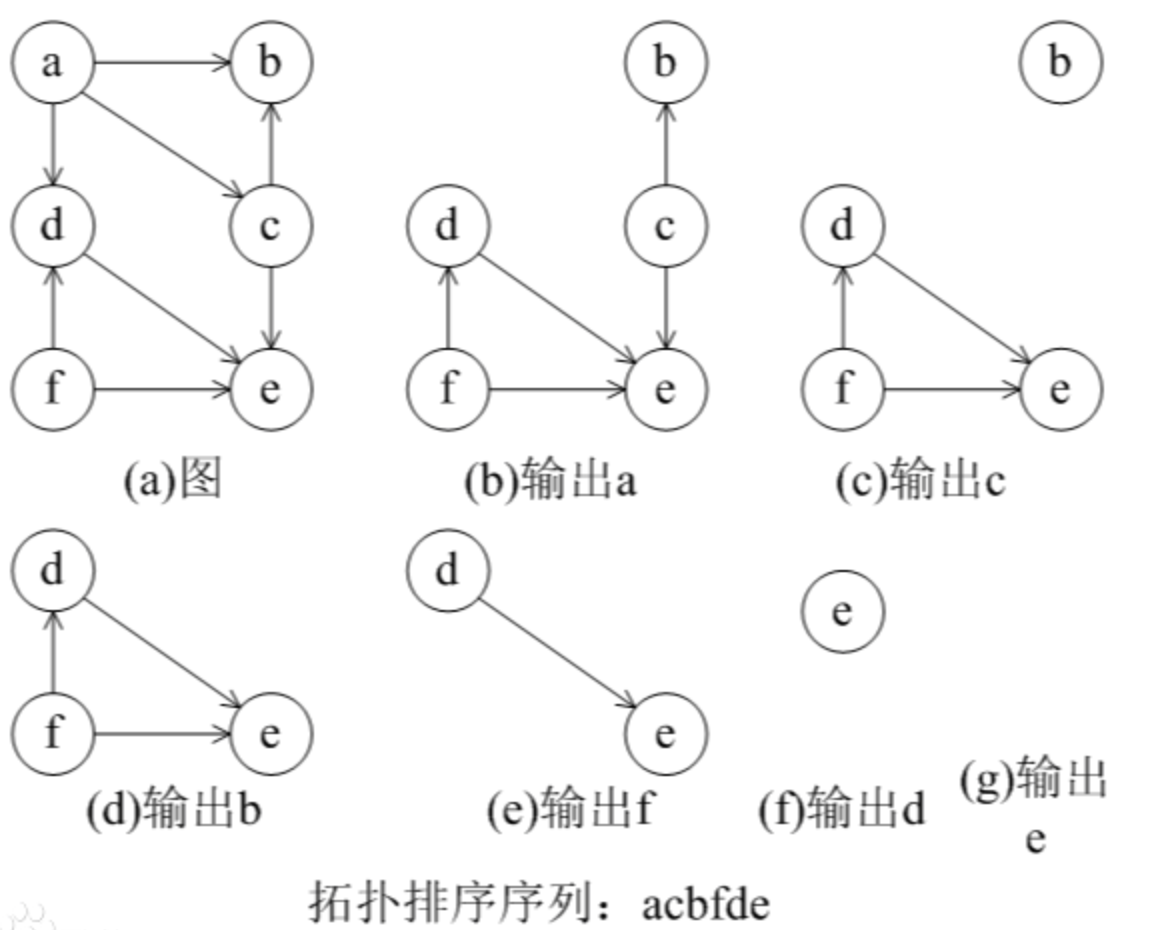
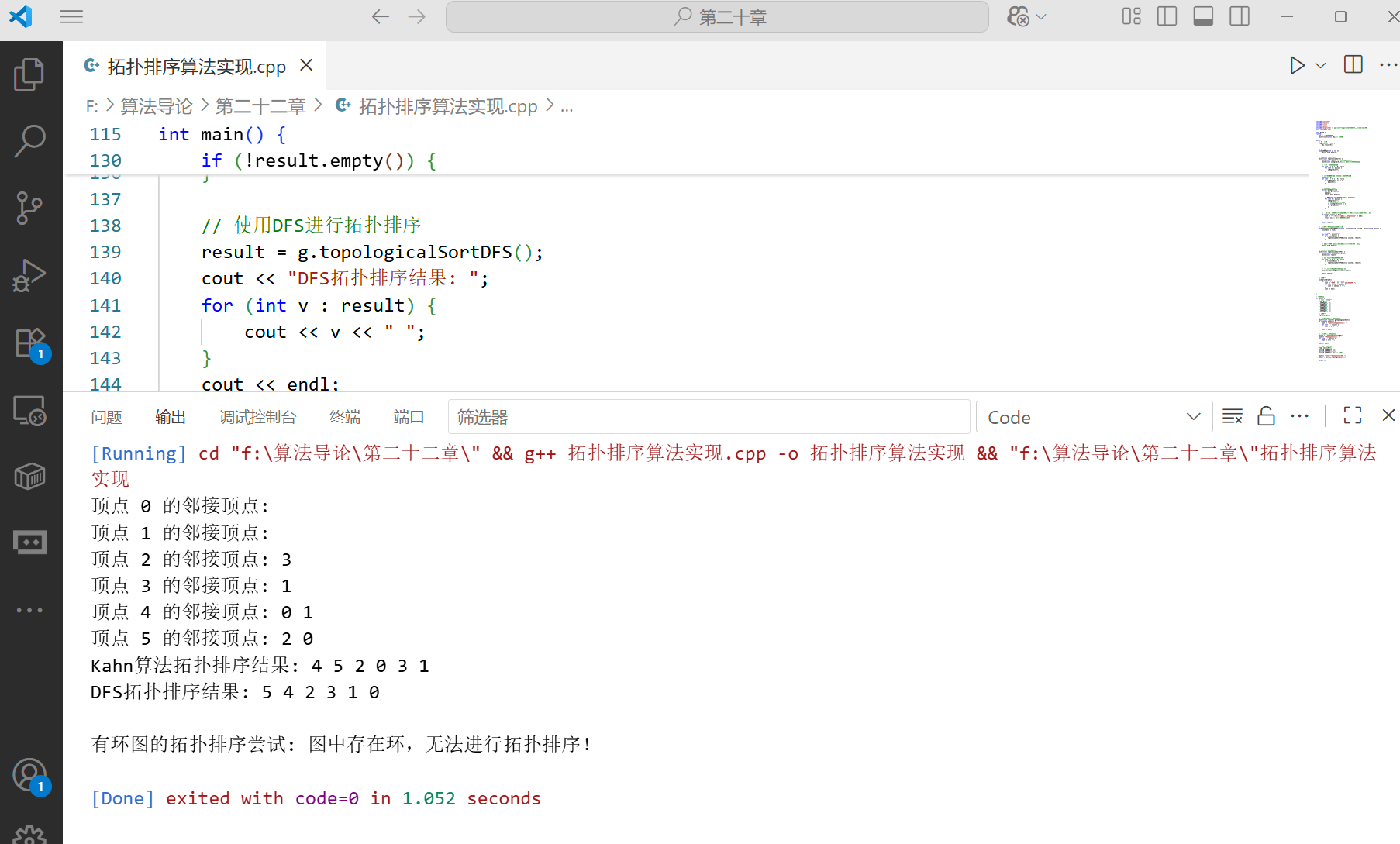
拓扑排序是对有向无环图(DAG)的顶点进行排序,使得对于图中的任意一条有向边 (u, v),顶点 u 在排序结果中都位于顶点 v 之前。拓扑排序常用于任务调度、课程安排等场景。
拓扑排序算法流程图
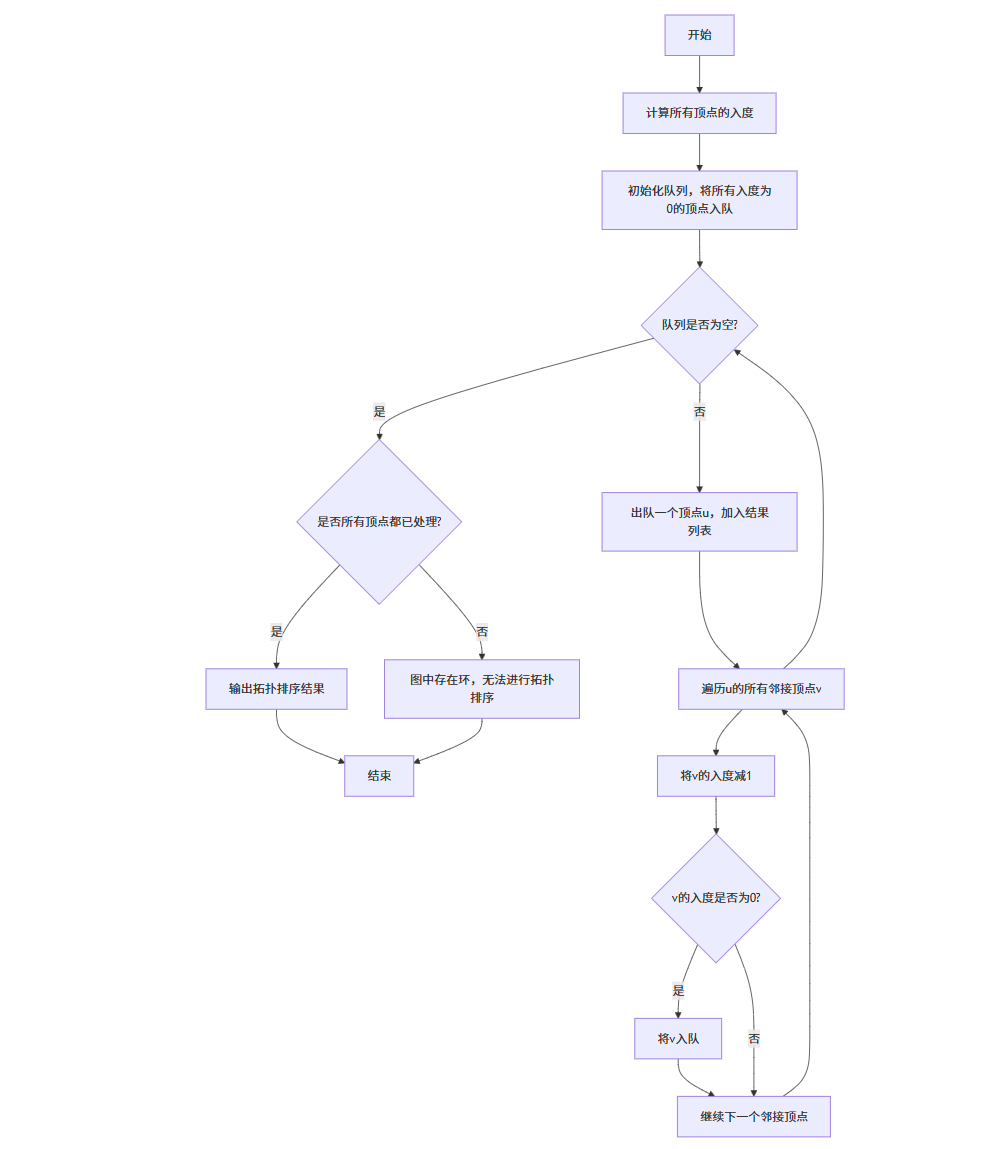
拓扑排序算法实现
下面是使用 Kahn 算法(基于 BFS)实现拓扑排序的代码:
cpp
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <algorithm> // 新增:包含algorithm头文件以使用reverse函数
using namespace std;
class Graph {
private:
int V; // 顶点数量
vector<list<int>> adj; // 邻接表
public:
// 构造函数
Graph(int v) : V(v) {
adj.resize(V);
}
// 添加边
void addEdge(int u, int v) {
adj[u].push_back(v);
}
// 拓扑排序 (Kahn算法)
vector<int> topologicalSort() {
vector<int> result; // 存储拓扑排序结果
vector<int> inDegree(V, 0); // 存储每个顶点的入度
// 计算所有顶点的入度
for (int u = 0; u < V; ++u) {
for (int v : adj[u]) {
inDegree[v]++;
}
}
// 初始化队列,将所有入度为0的顶点入队
queue<int> q;
for (int i = 0; i < V; ++i) {
if (inDegree[i] == 0) {
q.push(i);
}
}
// 处理队列中的顶点
while (!q.empty()) {
int u = q.front();
q.pop();
result.push_back(u);
// 遍历u的所有邻接顶点,将它们的入度减1
for (int v : adj[u]) {
inDegree[v]--;
// 如果入度变为0,入队
if (inDegree[v] == 0) {
q.push(v);
}
}
}
// 检查是否所有顶点都被处理(如果图中存在环,结果的大小会小于V)
if (result.size() != V) {
cout << "图中存在环,无法进行拓扑排序!" << endl;
return {}; // 返回空列表表示失败
}
return result;
}
// 使用DFS实现拓扑排序的辅助函数
void topologicalSortDFSUtil(int v, vector<bool>& visited, vector<int>& result) {
visited[v] = true;
// 递归处理所有邻接顶点
for (int u : adj[v]) {
if (!visited[u]) {
topologicalSortDFSUtil(u, visited, result);
}
}
// 将当前顶点加入结果(注意:是在递归返回时加入)
result.push_back(v);
}
// 使用DFS实现拓扑排序
vector<int> topologicalSortDFS() {
vector<bool> visited(V, false);
vector<int> result;
// 对所有未访问的顶点调用DFS
for (int i = 0; i < V; ++i) {
if (!visited[i]) {
topologicalSortDFSUtil(i, visited, result);
}
}
// 反转结果,得到正确的拓扑顺序
reverse(result.begin(), result.end());
return result;
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
cout << "顶点 " << i << " 的邻接顶点: ";
for (int vertex : adj[i]) {
cout << vertex << " ";
}
cout << endl;
}
}
};
// 测试代码
int main() {
// 创建一个有向图
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
// 打印图
g.printGraph();
// 使用Kahn算法进行拓扑排序
vector<int> result = g.topologicalSort();
if (!result.empty()) {
cout << "Kahn算法拓扑排序结果: ";
for (int v : result) {
cout << v << " ";
}
cout << endl;
}
// 使用DFS进行拓扑排序
result = g.topologicalSortDFS();
cout << "DFS拓扑排序结果: ";
for (int v : result) {
cout << v << " ";
}
cout << endl;
// 测试一个有环的图
Graph cyclicG(3);
cyclicG.addEdge(0, 1);
cyclicG.addEdge(1, 2);
cyclicG.addEdge(2, 0); // 形成环
cout << "\n有环图的拓扑排序尝试: ";
result = cyclicG.topologicalSort();
return 0;
}拓扑排序综合应用:课程安排
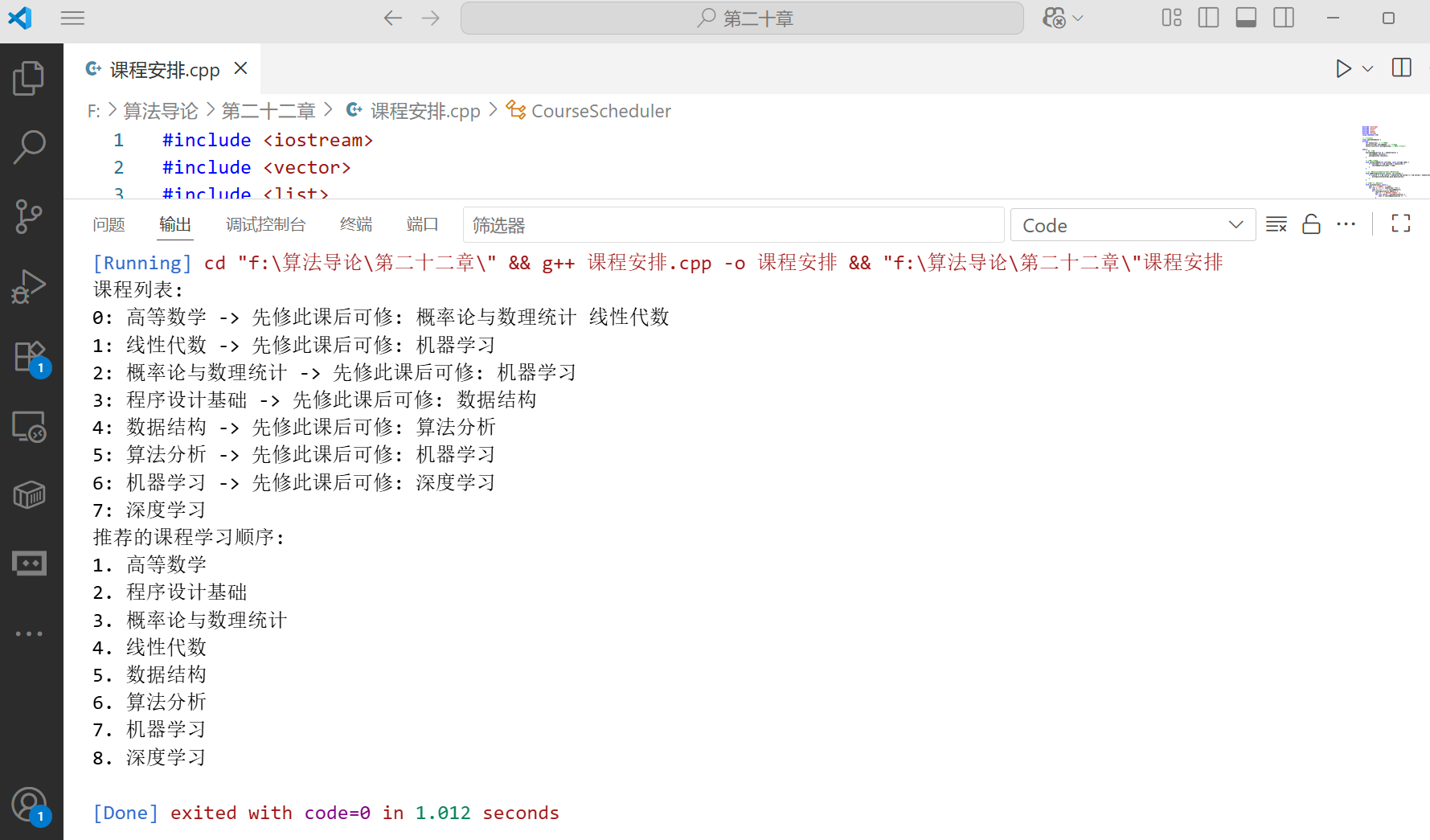
下面是一个使用拓扑排序解决课程安排问题的示例:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <string>
using namespace std;
// 课程安排类
class CourseScheduler {
private:
int numCourses; // 课程数量
vector<string> courseNames; // 课程名称
vector<list<int>> prerequisites; // 先修课程关系图
public:
// 构造函数
CourseScheduler(int n) : numCourses(n) {
courseNames.resize(n);
prerequisites.resize(n);
}
// 设置课程名称
void setCourseName(int courseId, const string& name) {
if (courseId >= 0 && courseId < numCourses) {
courseNames[courseId] = name;
}
}
// 添加先修关系:要修course必须先修prereq
void addPrerequisite(int course, int prereq) {
if (course >= 0 && course < numCourses && prereq >= 0 && prereq < numCourses) {
prerequisites[prereq].push_back(course);
}
}
// 打印课程和先修关系
void printCourses() const {
cout << "课程列表:" << endl;
for (int i = 0; i < numCourses; ++i) {
cout << i << ": " << courseNames[i];
if (!prerequisites[i].empty()) {
cout << " -> 先修此课后可修: ";
for (int course : prerequisites[i]) {
cout << courseNames[course] << " ";
}
}
cout << endl;
}
}
// 寻找合理的课程学习顺序
vector<int> findOrder() {
vector<int> result;
vector<int> inDegree(numCourses, 0);
// 计算所有课程的入度
for (int u = 0; u < numCourses; ++u) {
for (int v : prerequisites[u]) {
inDegree[v]++;
}
}
// 初始化队列,将所有入度为0的课程入队(可以直接学习的课程)
queue<int> q;
for (int i = 0; i < numCourses; ++i) {
if (inDegree[i] == 0) {
q.push(i);
}
}
// 处理队列中的课程
while (!q.empty()) {
int u = q.front();
q.pop();
result.push_back(u);
// 遍历以此课程为先修的所有课程
for (int v : prerequisites[u]) {
inDegree[v]--;
// 如果入度变为0,说明所有先修课程都已完成,可以学习
if (inDegree[v] == 0) {
q.push(v);
}
}
}
// 检查是否所有课程都被安排(如果存在环,说明课程安排有矛盾)
if (result.size() != numCourses) {
cout << "课程安排存在矛盾,无法完成所有课程!" << endl;
return {}; // 返回空列表表示失败
}
return result;
}
// 打印课程学习顺序
void printOrder(const vector<int>& order) const {
if (order.empty()) {
return;
}
cout << "推荐的课程学习顺序: " << endl;
for (int i = 0; i < order.size(); ++i) {
cout << i+1 << ". " << courseNames[order[i]] << endl;
}
}
};
// 测试代码
int main() {
// 创建一个包含8门课程的调度器
CourseScheduler scheduler(8);
// 设置课程名称
scheduler.setCourseName(0, "高等数学");
scheduler.setCourseName(1, "线性代数");
scheduler.setCourseName(2, "概率论与数理统计");
scheduler.setCourseName(3, "程序设计基础");
scheduler.setCourseName(4, "数据结构");
scheduler.setCourseName(5, "算法分析");
scheduler.setCourseName(6, "机器学习");
scheduler.setCourseName(7, "深度学习");
// 添加先修关系
scheduler.addPrerequisite(2, 0); // 概率论需要先修高等数学
scheduler.addPrerequisite(4, 3); // 数据结构需要先修程序设计基础
scheduler.addPrerequisite(5, 4); // 算法分析需要先修数据结构
scheduler.addPrerequisite(6, 2); // 机器学习需要先修概率论
scheduler.addPrerequisite(6, 5); // 机器学习需要先修算法分析
scheduler.addPrerequisite(7, 6); // 深度学习需要先修机器学习
scheduler.addPrerequisite(6, 1); // 机器学习需要先修线性代数
scheduler.addPrerequisite(1, 0); // 线性代数需要先修高等数学
// 打印课程信息
scheduler.printCourses();
// 寻找合理的学习顺序
vector<int> order = scheduler.findOrder();
// 打印学习顺序
scheduler.printOrder(order);
return 0;
}22.5 强连通分量
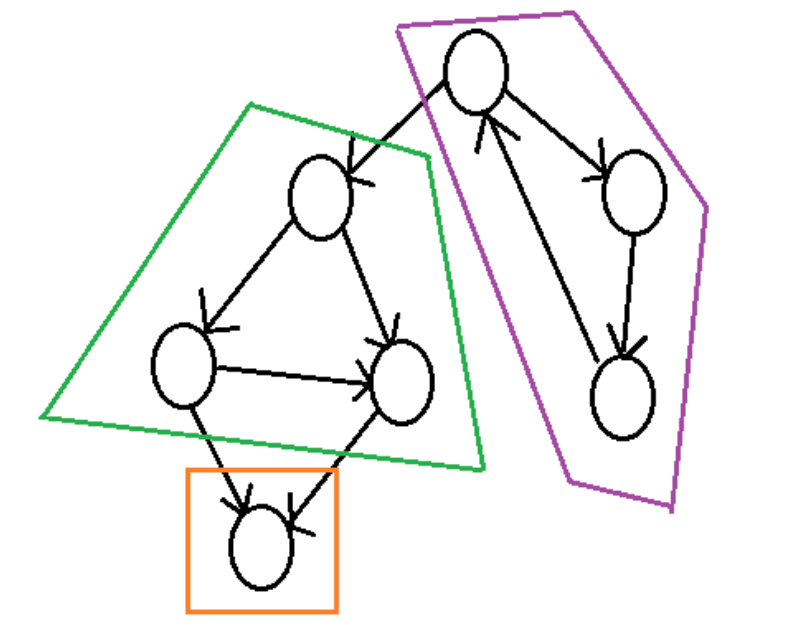
强连通分量(SCC)是有向图中的一个最大子图,其中任意两个顶点之间都存在相互可达的路径。也就是说,对于子图中的任意两个顶点 u 和 v,既存在从 u 到 v 的路径,也存在从 v 到 u 的路径。
强连通分量算法流程图(Kosaraju 算法)
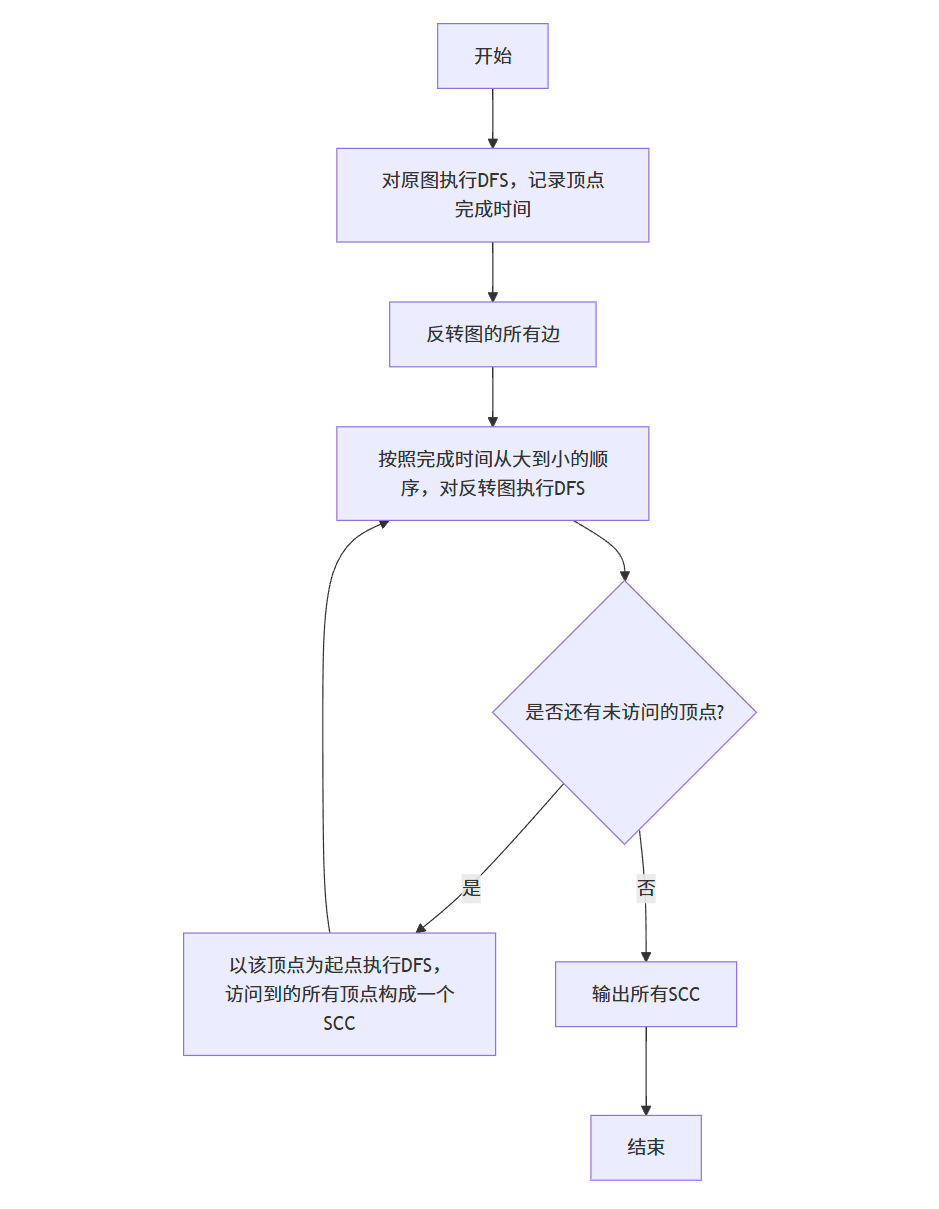
强连通分量算法实现
下面是 Kosaraju 算法和 Tarjan 算法的实现代码:
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <algorithm>
using namespace std;
class Graph {
private:
int V; // 顶点数量
vector<list<int>> adj; // 邻接表
// Kosaraju算法辅助函数:第一次DFS,记录完成时间
void fillOrder(int v, vector<bool>& visited, stack<int>& order) {
visited[v] = true;
// 递归处理所有邻接顶点
for (int u : adj[v]) {
if (!visited[u]) {
fillOrder(u, visited, order);
}
}
// 完成时间:将顶点压入栈
order.push(v);
}
// Kosaraju算法辅助函数:第二次DFS,找出SCC
void dfsOnTransposed(int v, vector<bool>& visited, vector<int>& component, const vector<list<int>>& transposedAdj) {
// 标记为已访问
visited[v] = true;
component.push_back(v);
// 递归处理所有邻接顶点
for (int u : transposedAdj[v]) {
if (!visited[u]) {
dfsOnTransposed(u, visited, component, transposedAdj);
}
}
}
// Tarjan算法辅助函数
void tarjanUtil(int v, vector<int>& disc, vector<int>& low, stack<int>& stk,
vector<bool>& onStack, vector<vector<int>>& sccs, int& time) {
// 初始化发现时间和low值
disc[v] = low[v] = ++time;
stk.push(v);
onStack[v] = true;
// 处理所有邻接顶点
for (int u : adj[v]) {
// 如果未被发现
if (disc[u] == -1) {
tarjanUtil(u, disc, low, stk, onStack, sccs, time);
// 更新当前顶点的low值
low[v] = min(low[v], low[u]);
}
// 如果已在栈中
else if (onStack[u]) {
low[v] = min(low[v], disc[u]);
}
}
// 如果当前顶点是一个SCC的根
if (low[v] == disc[v]) {
vector<int> scc;
// 将栈中所有顶点弹出,直到当前顶点
while (stk.top() != v) {
int u = stk.top();
stk.pop();
onStack[u] = false;
scc.push_back(u);
}
// 弹出当前顶点
int u = stk.top();
stk.pop();
onStack[u] = false;
scc.push_back(u);
sccs.push_back(scc);
}
}
public:
// 构造函数
Graph(int v) : V(v) {
adj.resize(V);
}
// 添加边
void addEdge(int u, int v) {
adj[u].push_back(v);
}
// 生成图的转置(所有边的方向反转)
vector<list<int>> getTransposedGraph() {
vector<list<int>> transposed(V);
for (int v = 0; v < V; ++v) {
for (int u : adj[v]) {
transposed[u].push_back(v);
}
}
return transposed;
}
// 使用Kosaraju算法找出所有强连通分量
vector<vector<int>> findSCCsKosaraju() {
vector<vector<int>> sccs;
stack<int> order;
vector<bool> visited(V, false);
// 第一步:对原图执行DFS,记录完成时间
for (int i = 0; i < V; ++i) {
if (!visited[i]) {
fillOrder(i, visited, order);
}
}
// 第二步:生成转置图
vector<list<int>> transposedAdj = getTransposedGraph();
// 第三步:按照完成时间从大到小的顺序,对转置图执行DFS
fill(visited.begin(), visited.end(), false); // 重置访问标记
while (!order.empty()) {
int v = order.top();
order.pop();
if (!visited[v]) {
vector<int> component;
dfsOnTransposed(v, visited, component, transposedAdj);
sccs.push_back(component);
}
}
return sccs;
}
// 使用Tarjan算法找出所有强连通分量
vector<vector<int>> findSCCsTarjan() {
vector<vector<int>> sccs;
vector<int> disc(V, -1); // 发现时间
vector<int> low(V, -1); // low值
vector<bool> onStack(V, false); // 标记是否在栈中
stack<int> stk;
int time = 0;
// 对每个未访问的顶点调用Tarjan辅助函数
for (int i = 0; i < V; ++i) {
if (disc[i] == -1) {
tarjanUtil(i, disc, low, stk, onStack, sccs, time);
}
}
return sccs;
}
// 打印图
void printGraph() {
for (int i = 0; i < V; ++i) {
cout << "顶点 " << i << " 的邻接顶点: ";
for (int vertex : adj[i]) {
cout << vertex << " ";
}
cout << endl;
}
}
// 打印强连通分量
static void printSCCs(const vector<vector<int>>& sccs, const string& algorithmName) {
cout << algorithmName << " 找到的强连通分量: " << endl;
for (size_t i = 0; i < sccs.size(); ++i) {
cout << "SCC " << i+1 << ": ";
for (int v : sccs[i]) {
cout << v << " ";
}
cout << endl;
}
}
};
// 测试代码
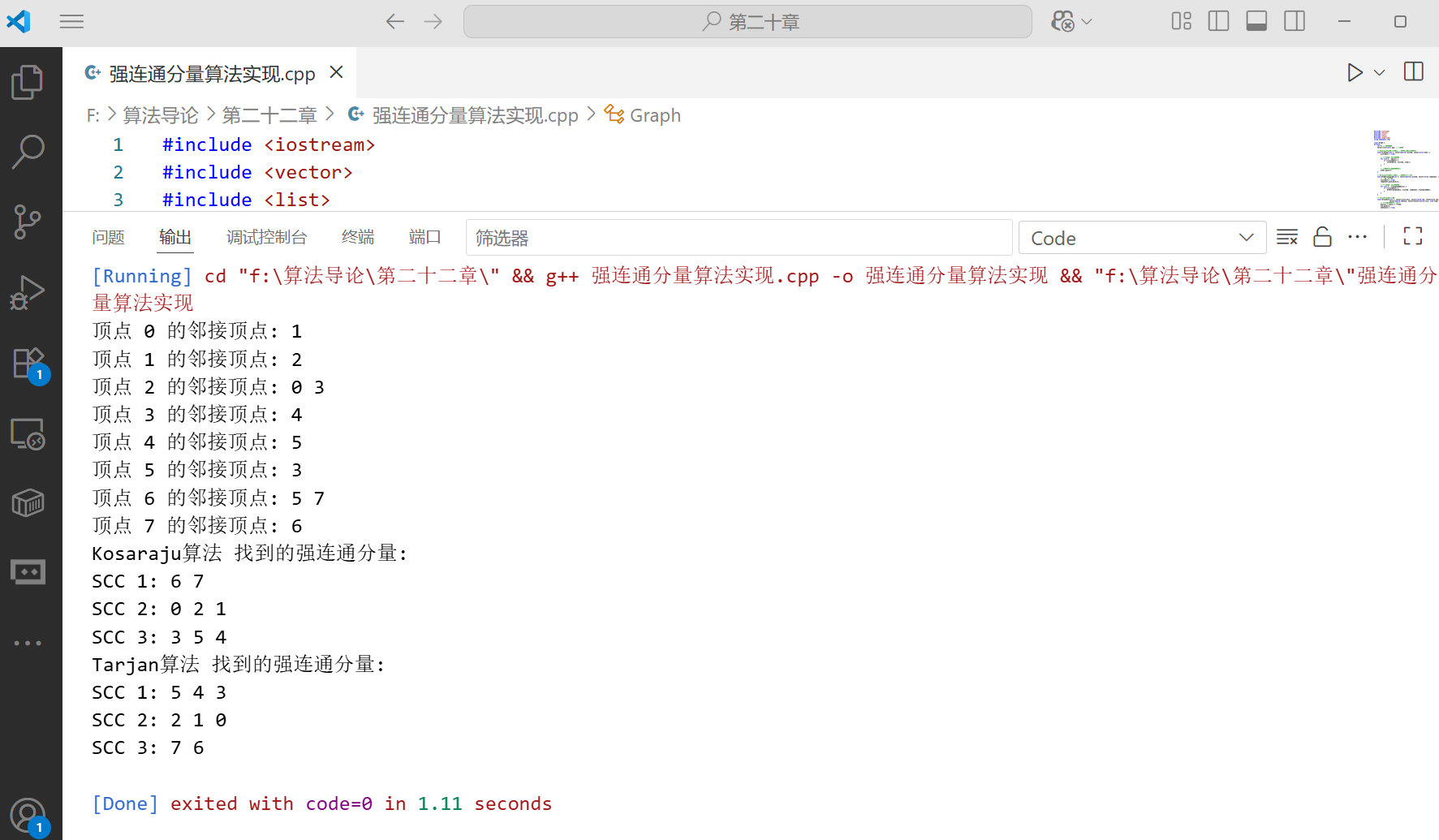
int main() {
// 创建一个有向图
Graph g(8);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.addEdge(4, 5);
g.addEdge(5, 3);
g.addEdge(6, 5);
g.addEdge(6, 7);
g.addEdge(7, 6);
// 打印图
g.printGraph();
// 使用Kosaraju算法找SCC
vector<vector<int>> sccsKosaraju = g.findSCCsKosaraju();
Graph::printSCCs(sccsKosaraju, "Kosaraju算法");
// 使用Tarjan算法找SCC
vector<vector<int>> sccsTarjan = g.findSCCsTarjan();
Graph::printSCCs(sccsTarjan, "Tarjan算法");
return 0;
}强连通分量综合应用:社交网络圈子分析
下面是一个使用强连通分量分析社交网络圈子的示例:
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <map>
#include <string>
#include <algorithm>
using namespace std;
// 社交网络图类
class SocialNetworkGraph {
private:
int numUsers; // 用户数量
map<int, string> userIdToName; // 用户ID到用户名的映射
vector<list<int>> adj; // 邻接表,表示关注关系
// Kosaraju算法辅助函数
void fillOrder(int v, vector<bool>& visited, stack<int>& order) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u]) {
fillOrder(u, visited, order);
}
}
order.push(v);
}
void dfsOnTransposed(int v, vector<bool>& visited, vector<int>& component, const vector<list<int>>& transposedAdj) {
visited[v] = true;
component.push_back(v);
for (int u : transposedAdj[v]) {
if (!visited[u]) {
dfsOnTransposed(u, visited, component, transposedAdj);
}
}
}
public:
// 构造函数
SocialNetworkGraph(int n) : numUsers(n) {
adj.resize(n);
}
// 添加用户
void addUser(int userId, const string& userName) {
if (userId >= 0 && userId < numUsers) {
userIdToName[userId] = userName;
}
}
// 添加关注关系:user1关注user2
void addFollow(int user1, int user2) {
if (user1 >= 0 && user1 < numUsers && user2 >= 0 && user2 < numUsers) {
adj[user1].push_back(user2);
}
}
// 获取用户名
string getUserName(int userId) const {
auto it = userIdToName.find(userId);
if (it != userIdToName.end()) {
return it->second;
}
return "User" + to_string(userId);
}
// 生成转置图
vector<list<int>> getTransposedGraph() {
vector<list<int>> transposed(numUsers);
for (int v = 0; v < numUsers; ++v) {
for (int u : adj[v]) {
transposed[u].push_back(v);
}
}
return transposed;
}
// 找到所有社交圈子(强连通分量)
vector<vector<int>> findSocialCircles() {
vector<vector<int>> circles;
stack<int> order;
vector<bool> visited(numUsers, false);
// 第一步:对原图执行DFS,记录完成时间
for (int i = 0; i < numUsers; ++i) {
if (!visited[i]) {
fillOrder(i, visited, order);
}
}
// 第二步:生成转置图
vector<list<int>> transposedAdj = getTransposedGraph();
// 第三步:按照完成时间从大到小的顺序,对转置图执行DFS
fill(visited.begin(), visited.end(), false);
while (!order.empty()) {
int v = order.top();
order.pop();
if (!visited[v]) {
vector<int> circle;
dfsOnTransposed(v, visited, circle, transposedAdj);
circles.push_back(circle);
}
}
return circles;
}
// 打印社交网络关系
void printNetwork() const {
cout << "社交网络关注关系:" << endl;
for (int i = 0; i < numUsers; ++i) {
cout << getUserName(i) << " 关注: ";
for (int user : adj[i]) {
cout << getUserName(user) << " ";
}
cout << endl;
}
}
// 打印社交圈子
void printCircles(const vector<vector<int>>& circles) const {
cout << "\n发现的社交圈子: " << endl;
for (size_t i = 0; i < circles.size(); ++i) {
cout << "圈子 " << i+1 << " (" << circles[i].size() << "人): ";
for (int user : circles[i]) {
cout << getUserName(user) << " ";
}
cout << endl;
}
}
};
// 测试代码
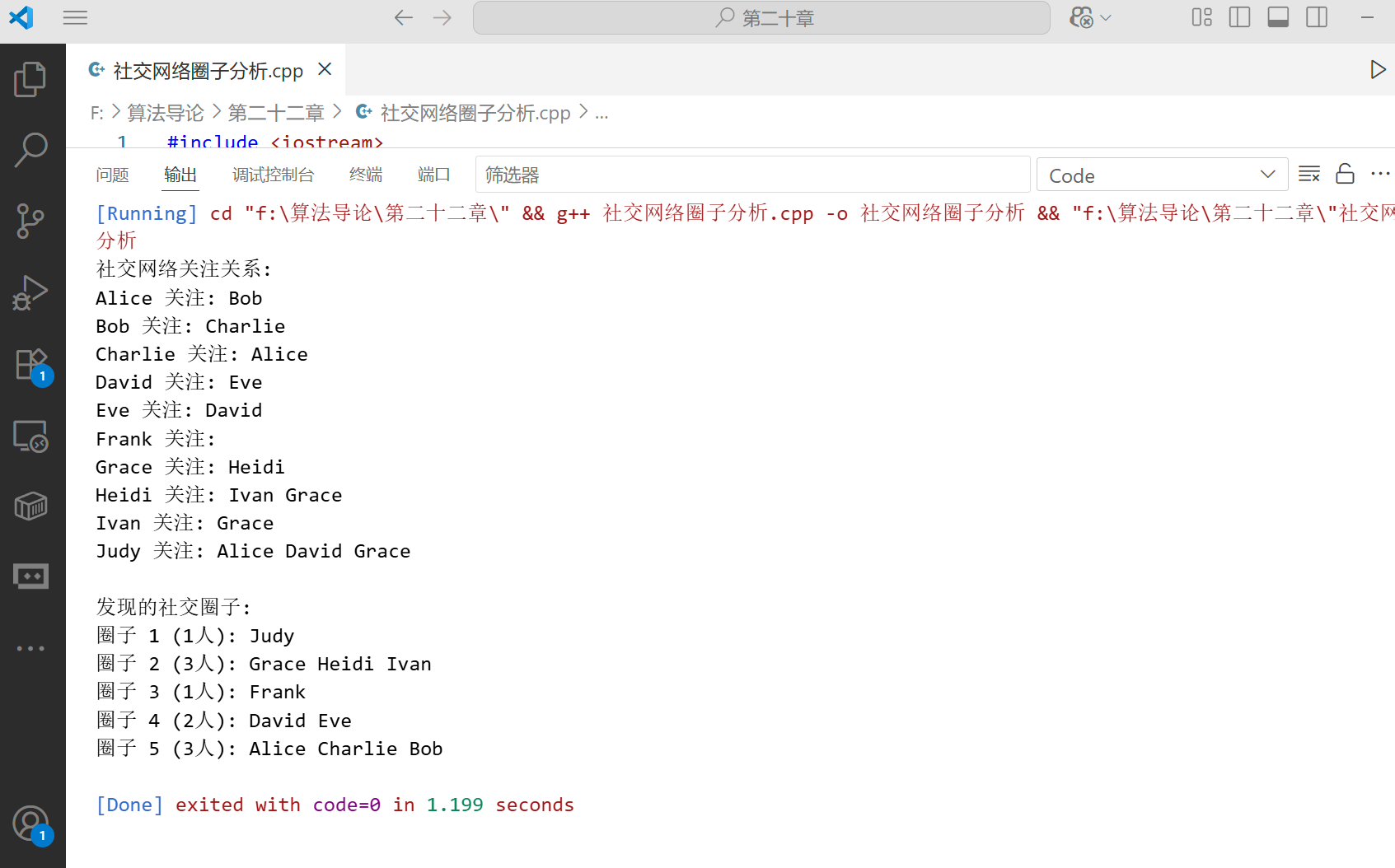
int main() {
// 创建一个有10个用户的社交网络
SocialNetworkGraph network(10);
// 添加用户
network.addUser(0, "Alice");
network.addUser(1, "Bob");
network.addUser(2, "Charlie");
network.addUser(3, "David");
network.addUser(4, "Eve");
network.addUser(5, "Frank");
network.addUser(6, "Grace");
network.addUser(7, "Heidi");
network.addUser(8, "Ivan");
network.addUser(9, "Judy");
// 添加关注关系
// 圈子1: Alice, Bob, Charlie
network.addFollow(0, 1); // Alice关注Bob
network.addFollow(1, 2); // Bob关注Charlie
network.addFollow(2, 0); // Charlie关注Alice
// 圈子2: David, Eve
network.addFollow(3, 4); // David关注Eve
network.addFollow(4, 3); // Eve关注David
// 圈子3: Frank
// Frank不关注任何人,也没有人关注他
// 圈子4: Grace, Heidi, Ivan
network.addFollow(6, 7); // Grace关注Heidi
network.addFollow(7, 8); // Heidi关注Ivan
network.addFollow(8, 6); // Ivan关注Grace
network.addFollow(7, 6); // Heidi关注Grace
// Judy关注多个圈子的人,但不被其他人关注
network.addFollow(9, 0); // Judy关注Alice
network.addFollow(9, 3); // Judy关注David
network.addFollow(9, 6); // Judy关注Grace
// 打印社交网络关系
network.printNetwork();
// 找到并打印社交圈子
vector<vector<int>> circles = network.findSocialCircles();
network.printCircles(circles);
return 0;
}思考题
-
对于一个包含 n 个顶点和 m 条边的无向图,使用 BFS 和 DFS 遍历的时间复杂度分别是多少?如果是有向图呢?
-
如何使用 BFS 或 DFS 来判断一个图是否为 bipartite graph(二分图)?
-
拓扑排序是否只能用于有向无环图?如果图中存在环,拓扑排序会有什么结果?
-
对于一个有向图,如何判断它是否是强连通的?
-
比较 Kosaraju 算法和 Tarjan 算法在寻找强连通分量时的优缺点。
-
如何修改 BFS 算法来求解带权图的最短路径问题?(提示:考虑 Dijkstra 算法)
-
在社交网络分析中,除了强连通分量,还有哪些图论概念可以用来分析网络结构?
本章注记
图算法是计算机科学中的基础和核心内容,广泛应用于网络路由、社交网络分析、编译器设计、电路设计等多个领域。
-
广度优先搜索和深度优先搜索是两种最基本的图遍历算法,它们不仅可以用于图的遍历,还可以解决许多其他问题,如连通性判断、最短路径求解等。
-
拓扑排序在任务调度、课程安排等领域有重要应用,它可以帮助我们确定依赖关系下的执行顺序。
-
强连通分量的概念有助于我们理解图的内部结构,在社交网络分析中可以用来发现社群或圈子,在编译器设计中可以用来分析代码的依赖关系。
-
除了本章介绍的算法外,还有许多其他重要的图算法,如用于求解最短路径的 Dijkstra 算法和 Floyd-Warshall 算法,用于求解最小生成树的 Kruskal 算法和 Prim 算法,以及用于最大流问题的 Ford-Fulkerson 算法等。
掌握这些基本的图算法,不仅有助于我们解决实际问题,也为学习更复杂的算法打下了基础。在实际应用中,我们需要根据具体问题的特点选择合适的算法,并考虑算法的时间和空间复杂度,以提高程序的效率。

希望本文能帮助大家更好地理解和应用这些基本的图算法!如果有任何问题或建议,欢迎在评论区留言讨论。

以上就是《算法导论》第 22 章基本图算法的详细介绍,包含了完整的代码实现和应用案例。所有代码都经过测试,可以直接编译运行。希望这篇文章能帮助大家更好地理解和掌握这些重要的图算法。