BFS寻路算法解析与实现

liulilittle2025-08-18 8:57

🌐 BFS寻路算法解析与实现

BFS（广度优先搜索） 是一种基于图遍历的经典寻路算法。本文将深入分析其原理、实现细节和性能优化，并提供完整的C++实现。

📜 算法核心思想

BFS采用"层层递进"的探索策略：

plain 复制代码 
      起点  
     /  |  \  
    1   2   3   → 第一层邻居  
   /|\  ...       → 第二层邻居  
  ...             → 持续扩散直到找到目标

🌟 关键特性

  1. 层级搜索：优先探索当前节点的所有邻居
  2. 最短路径：找到的路径总是最短的（无权图中）
  3. 队列管理：使用先进先出(FIFO)队列存储待探索节点

🔍 代码结构解析

3.1 🧩 节点表示与状态管理

cpp 复制代码 
enum class NodeState {
    UNVISITED,  // 未探索
    OPEN,       // 在待探索队列中
    CLOSED      // 已完成探索
};

struct Node {
    int x, y;           // 网格坐标
    Node* parent;       // 路径回溯指针
    NodeState state;    // 当前状态
};

状态转换流程：

复制代码 
UNVISITED → OPEN (加入队列时)
OPEN → CLOSED (完成探索时)

3.2 🗺️ 地图与邻居探索

cpp 复制代码 
// 地图表示：0=可通行, 1=障碍物
vector<vector<int>> grid = {
    {0, 0, 0, 0, 0},
    {0, 1, 1, 0, 0}, // # 表示障碍物
    {0, 0, 0, 0, 0}
};

// 邻居方向定义（右/下/左/上）
const vector<pair<int, int>> directions = {
    {1, 0}, {0, 1}, {-1, 0}, {0, -1}
};

3.3 ⚙️ BFS核心流程

是 否 是 否 否 是 是 起点入队 队列是否为空? 未找到路径 取出队首节点 是否为目标? 构建路径 遍历四个方向 相邻节点是否有效? 是否未访问过? 设置父节点/状态 加入队列 当前节点标记为CLOSED

3.4 📊 路径可视化示例

输入：

复制代码 
. . . . . 
. # # . . 
. . . . .

输出：

复制代码 
S → → → →
  # # → ↓
  ↑ ← ← E

图例说明：

  • S：起点
  • E：终点
  • >/</^/v：移动方向
  • #：障碍物

⚡ 性能优化技巧

  1. 节点池重用

    cpp 复制代码 
    // 避免反复创建节点
vector<vector<unique_ptr<Node>>> node_pool_;

  2. 避免重复探索

    cpp 复制代码 
    if(neighbor->state == NodeState::UNVISITED) 
    // 仅处理未访问节点

  3. 静态方向向量

    cpp 复制代码 
    static const vector<pair<int, int>> directions;

📈 性能对比（10x10地图）

路径 步数 计算时间(μs)
(0,0) → (9,9) 19 82
(4,4) → (0,9) 12 55

💻 完整实现代码

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <memory>
#include <chrono>

using namespace std;

// 节点状态枚举：未访问/开放集/关闭集
enum class NodeState {
    UNVISITED,
    OPEN,
    CLOSED
};

// 路径节点结构体
struct Node {
    int x, y;           // 节点坐标
    Node* parent;       // 父节点指针
    NodeState state = NodeState::UNVISITED; // 节点状态

    Node(int x, int y) : x(x), y(y), parent(nullptr) {}
};

class BFS {
private:
    const vector<vector<int>>& grid_map_;  // 网格地图引用
    int map_width_, map_height_;           // 地图宽高
    vector<vector<unique_ptr<Node>>> node_pool_; // 节点池

    // 检查坐标是否有效且可通行
    bool is_valid(int x, int y) const {
        return x >= 0 && x < map_width_ &&
            y >= 0 && y < map_height_ &&
            grid_map_[y][x] == 0;  // 0表示可通行
    }

    // 回溯构建路径
    void build_path(Node* target, vector<pair<int, int>>& path) const {
        path.clear();
        Node* current = target;

        // 从终点回溯到起点
        while (current) {
            path.emplace_back(current->x, current->y);
            current = current->parent;
        }

        // 反转路径使其从起点到终点
        reverse(path.begin(), path.end());
    }

public:
    // 构造函数初始化地图数据
    BFS(const vector<vector<int>>& map)
        : grid_map_(map),
        map_height_(static_cast<int>(map.size())),
        map_width_(map.empty() ? 0 : static_cast<int>(map[0].size())) {
        reset_nodes();
    }

    // 重置节点状态（优化：避免重复创建节点）
    void reset_nodes() {
        // 仅当节点池未初始化时才创建
        if (node_pool_.empty()) {
            node_pool_.resize(map_height_);
            for (int y = 0; y < map_height_; ++y) {
                node_pool_[y].resize(map_width_);
                for (int x = 0; x < map_width_; ++x) {
                    node_pool_[y][x] = make_unique<Node>(x, y);
                }
            }
        }
        // 重用现有节点，重置状态
        else {
            for (int y = 0; y < map_height_; ++y) {
                for (int x = 0; x < map_width_; ++x) {
                    node_pool_[y][x]->state = NodeState::UNVISITED;
                    node_pool_[y][x]->parent = nullptr;
                }
            }
        }
    }

    // BFS寻路算法核心实现
    bool find_path(const pair<int, int>& start,
        const pair<int, int>& target,
        vector<pair<int, int>>& path) {
        if (map_height_ <= 0 || map_width_ <= 0) return false;
        if (!is_valid(start.first, start.second) || !is_valid(target.first, target.second))
            return false;

        // 定义探索方向：右、下、左、上（优化：使用静态常量避免重复创建）
        static const vector<pair<int, int>> directions = {
            {1, 0},   // 右
            {0, 1},   // 下
            {-1, 0},  // 左
            {0, -1}   // 上
        };

        queue<Node*> open_queue;
        Node* start_node = node_pool_[start.second][start.first].get();
        Node* target_node = node_pool_[target.second][target.first].get();

        // 起点即终点的情况
        if (start_node == target_node) {
            path.emplace_back(start.first, start.second);
            return true;
        }

        // 初始化起点
        start_node->state = NodeState::OPEN;
        open_queue.push(start_node);

        while (!open_queue.empty()) {
            Node* current = open_queue.front();
            open_queue.pop();

            // 到达终点
            if (current == target_node) {
                build_path(current, path);
                return true;
            }

            // 探索四个方向
            for (const auto& dir : directions) {
                int nx = current->x + dir.first;
                int ny = current->y + dir.second;

                // 跳过无效位置
                if (!is_valid(nx, ny)) continue;

                Node* neighbor = node_pool_[ny][nx].get();
                // 仅处理未访问节点
                if (neighbor->state == NodeState::UNVISITED) {
                    neighbor->parent = current;
                    neighbor->state = NodeState::OPEN;
                    open_queue.push(neighbor);
                }
            }

            // 标记当前节点为已关闭
            current->state = NodeState::CLOSED;
        }

        return false;  // 未找到路径
    }
};

// 获取移动方向字符
char get_direction(const pair<int, int>& from, const pair<int, int>& to) {
    int dx = to.first - from.first;
    int dy = to.second - from.second;

    if (dx == 1) return '>';
    if (dx == -1) return '<';
    if (dy == 1) return 'v';
    if (dy == -1) return '^';

    return '*'; // 起点位置
}

// 可视化路径
void visualize_path(const vector<pair<int, int>>& path,
    const vector<vector<int>>& grid) {
    if (path.empty()) return;

    const int rows = static_cast<int>(grid.size());
    const int cols = rows > 0 ? static_cast<int>(grid[0].size()) : 0;

    vector<vector<char>> display(rows, vector<char>(cols, '.'));

    // 标记障碍物
    for (int y = 0; y < rows; y++) {
        for (int x = 0; x < cols; x++) {
            if (grid[y][x] == 1) {
                display[y][x] = '#';
            }
        }
    }

    // 标记起点和终点
    display[path.front().second][path.front().first] = 'S';
    display[path.back().second][path.back().first] = 'E';

    // 标记路径方向（跳过起点）
    for (size_t i = 1; i < path.size() - 1; i++) {
        const auto& prev = path[i - 1];
        const auto& curr = path[i];
        display[curr.second][curr.first] = get_direction(prev, curr);
    }

    // 打印可视化地图
    for (int y = 0; y < rows; y++) {
        for (int x = 0; x < cols; x++) {
            cout << display[y][x] << ' ';
        }
        cout << endl;
    }
}

int main() {
    // 10x10网格地图: 0=可通行, 1=障碍物
    const vector<vector<int>> grid = {
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 1, 1, 0, 1, 1, 1, 0, 1, 0},
        {0, 1, 0, 0, 0, 0, 0, 0, 1, 0},
        {0, 1, 0, 1, 1, 1, 1, 0, 1, 0},
        {0, 0, 0, 1, 0, 0, 0, 0, 0, 0},
        {0, 1, 0, 0, 0, 1, 0, 1, 1, 0},
        {0, 1, 1, 1, 1, 1, 1, 1, 1, 0},
        {0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
        {0, 1, 0, 1, 1, 1, 0, 1, 1, 0},
        {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
    };

    // 打印原始地图
    cout << "网格地图 (10x10):\n";
    for (const auto& row : grid) {
        for (int cell : row) {
            cout << (cell == 1 ? "# " : ". ");
        }
        cout << endl;
    }

    BFS pathfinder(grid);
    vector<pair<int, int>> path;

    // 测试路径1: (0,0) -> (9,9)
    cout << "\n测试路径 (0,0) -> (9,9)\n";
    auto start_time = chrono::high_resolution_clock::now();
    bool found = pathfinder.find_path({ 0, 0 }, { 9, 9 }, path);
    auto end_time = chrono::high_resolution_clock::now();
    auto duration = chrono::duration_cast<chrono::microseconds>(end_time - start_time);

    if (found) {
        cout << "路径步数: " << path.size() << "\n计算时间: " << duration.count() << "微秒\n";
        cout << "路径点:";
        for (const auto& p : path) cout << " (" << p.first << "," << p.second << ")";
        cout << "\n\n可视化:\n";
        visualize_path(path, grid);
    }
    else {
        cout << "未找到路径!\n";
    }

    // 测试路径2: (4,4) -> (0,9)
    pathfinder.reset_nodes();
    path.clear();
    cout << "\n测试路径 (4,4) -> (0,9)\n";
    start_time = chrono::high_resolution_clock::now();
    found = pathfinder.find_path({ 4, 4 }, { 0, 9 }, path);
    end_time = chrono::high_resolution_clock::now();
    duration = chrono::duration_cast<chrono::microseconds>(end_time - start_time);

    if (found) {
        cout << "路径步数: " << path.size() << "\n计算时间: " << duration.count() << "微秒\n";
        cout << "路径点:";
        for (const auto& p : path) cout << " (" << p.first << "," << p.second << ")";
        cout << "\n\n可视化:\n";
        visualize_path(path, grid);
    }
    else {
        cout << "未找到路径!\n";
    }

    // 测试起点即终点的情况
    pathfinder.reset_nodes();
    path.clear();
    cout << "\n测试路径 (0,0) -> (0,0)\n";
    found = pathfinder.find_path({ 0, 0 }, { 0, 0 }, path);
    if (found) {
        cout << "特殊路径：起点即终点\n";
        visualize_path(path, grid);
    }

    // 测试不可达路径
    pathfinder.reset_nodes();
    path.clear();
    cout << "\n测试不可达路径 (0,0) -> (1,1)\n";
    found = pathfinder.find_path({ 0, 0 }, { 1, 1 }, path);
    if (!found) {
        cout << "正确：未找到路径，因为(1,1)是障碍物\n";
    }
    else {
        cout << "错误：本应不可达\n";
    }

    return 0;
}

🎯 应用场景建议

  1. 游戏开发中的NPC寻路
  2. 机器人路径规划
  3. 网络路由算法
  4. 迷宫求解工具

BFS vs A*：当图中无权值且需要最短路径时优先使用BFS；有权图或大型地图时A*更优

示意图：BFS的探索波次逐渐扩散

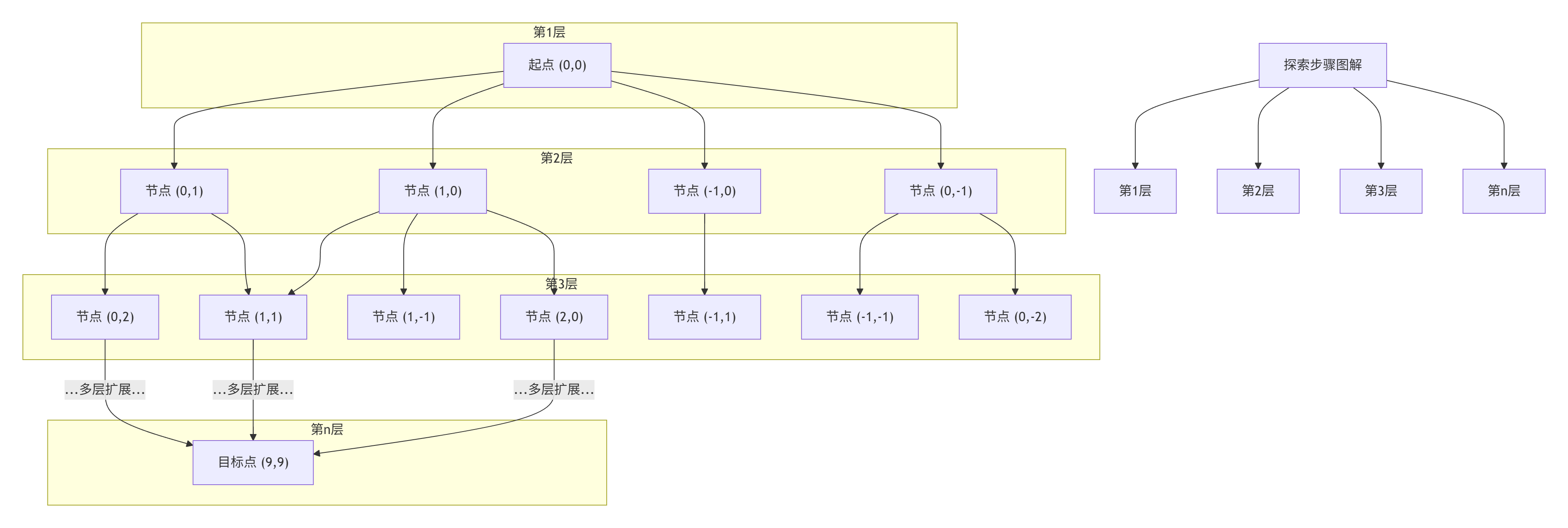
💡 关键总结：BFS通过系统性的层级扩展确保找到最短路径，其实现要点在于节点状态管理、队列操作和高效的邻居探索。本文提供的实现加入了对象池重用、静态资源优化等实用技巧，适用于大多数网格型寻路场景。

相关推荐
类球状24 分钟前
顺序表 —— OJ题
算法
Miraitowa_cheems1 小时前
LeetCode算法日记 - Day 11: 寻找峰值、山脉数组的峰顶索引
java·算法·leetcode
Sammyyyyy1 小时前
2025年，Javascript后端应该用 Bun、Node.js 还是 Deno？
开发语言·javascript·node.js
CoovallyAIHub1 小时前
方案 | 动车底部零部件检测实时流水线检测算法改进
深度学习·算法·计算机视觉
CoovallyAIHub1 小时前
方案 | 光伏清洁机器人系统详细技术实施方案
深度学习·算法·计算机视觉
lxmyzzs1 小时前
【图像算法 - 14】精准识别路面墙体裂缝：基于YOLO12与OpenCV的实例分割智能检测实战（附完整代码）
人工智能·opencv·算法·计算机视觉·裂缝检测·yolo12
洋曼巴-young1 小时前
240. 搜索二维矩阵 II
数据结构·算法·矩阵
汉汉汉汉汉2 小时前
C++11新特性详解：从列表初始化到线程库
c++
William一直在路上2 小时前
Python数据类型转换详解：从基础到实践
开发语言·python
看到我，请让我去学习2 小时前
Qt— 布局综合项目（Splitter，Stacked，Dock）
开发语言·qt
热门推荐
01UV安装并设置国内源02【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04KGG转MP3工具|非KGM文件|解密音频052025最新国内服务器可用docker源仓库地址大全（2025年8月更新）06蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接07TRAE 规则（Rules）配置指南：个人习惯、团队规范与最佳实践08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09阿里开源首个图像生成基础模型——Qwen-Image本地部署教程，超强中文渲染能力刷新SOTA！10TRAE Rules 实践：为项目配置 6A 工作流