算法奇妙屋(二十四)-二维费用的背包问题、似包非包问题、卡特兰数问题(动态规划)

文章目录

[一. 力扣 $474. 一和零$ (https://leetcode.cn/problems/ones-and-zeroes/description/)](#一. 力扣 474. 一和零)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [4. 优化](#4. 优化)
- [5. 优化后的代码](#5. 优化后的代码)
[二. 力扣 $879. 盈利计划$ (https://leetcode.cn/problems/profitable-schemes/description/)](#二. 力扣 879. 盈利计划)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [4. 优化后的代码](#4. 优化后的代码)
[三. (似包非包问题) 力扣 $377. 组合总和 Ⅳ$ (https://leetcode.cn/problems/combination-sum-iv/description/)](#三. (似包非包问题) 力扣 377. 组合总和 Ⅳ)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
[四. (卡特兰数) 力扣 $96. 不同的二叉搜索树$ (https://leetcode.cn/problems/unique-binary-search-trees/description/)](#四. (卡特兰数) 力扣 96. 不同的二叉搜索树)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)

一. 力扣 474. 一和零

1. 题目解析

我们的第一道二维费用的背包问题模板, 这里我们会在题目解析来梳理什么是二维费用

2. 算法原理

和01背包问题很相似

3. 代码

java 复制代码

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int[][][] dp = new int[len + 1][m + 1][n + 1];
        for (int i = 1; i <= len; i++) {
            int a = 0;
            int b = 0;
            for (char ch : strs[i - 1].toCharArray()) {
                if (ch == '0') {
                    a++;
                } else {
                    b++;
                }
            }
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    dp[i][j][k] = dp[i - 1][j][k];

                    if (j >= a && k >= b) {
                        dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);
                    }
                }
            }
        }
        return dp[len][m][n];
    }
}

4. 优化

这道题和01背包的优化原理也基本一致, 直接摘抄01背包的优化原理

5. 优化后的代码

删除第一维度, j 和 k的遍历顺序颠倒, 范围缩小

java 复制代码

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= len; i++) {
            int a = 0;
            int b = 0;
            for (char ch : strs[i - 1].toCharArray()) {
                if (ch == '0') {
                    a++;
                } else {
                    b++;
                }
            }
            for (int j = m; j >= a; j--) {
                for (int k = n; k >= b; k--) {
                    dp[j][k] = Math.max(dp[j][k], dp[j - a][k - b] + 1);
                }
            }
        }
        return dp[m][n];
    }
}

二. 力扣 879. 盈利计划

1. 题目解析

题目较难理解, 这里主要是讲解题目含义

2. 算法原理

3. 代码

java 复制代码

class Solution {
    public int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {
        // 建表
        int len = group.length;
        int[][][] dp = new int[len + 1][n + 1][minProfit + 1];
        int mod = (int)1e9 + 7;
        // 初始化
        for (int j = 0; j <= n; j++) {
            dp[0][j][0] = 1;
        }
        // 填表
        for (int i = 1; i <= len; i++) {
            for (int j = 0; j <= n; j++) {
                for (int k = 0; k <= minProfit; k++) {
                    dp[i][j][k] = dp[i - 1][j][k] % mod;
                    if (j >= group[i - 1]) {
                        dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - group[i - 1]][Math.max(0, k - profit[i - 1])]) % mod;
                    }
                }
            }
        }
        // 返回结果
        return dp[len][n][minProfit];
    }
}

4. 优化后的代码

删除第一维度, j 和 k的遍历顺序颠倒, 范围缩小

java 复制代码

class Solution {
    public int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {
        // 建表
        int len = group.length;
        int[][] dp = new int[n + 1][minProfit + 1];
        int mod = (int) 1e9 + 7;
        // 初始化
        for (int j = 0; j <= n; j++) {
            dp[j][0] = 1;
        }
        // 填表
        for (int i = 1; i <= len; i++) {
            for (int j = n; j >= group[i - 1]; j--) {
                for (int k = minProfit; k >= 0; k--) {
                    dp[j][k] = (dp[j][k] + dp[j - group[i - 1]][Math.max(0, k - profit[i - 1])]) % mod;
                }
            }
        }
        // 返回结果
        return dp[n][minProfit];
    }
}

三. (似包非包问题) 力扣 377. 组合总和 Ⅳ

1. 题目解析

注意理解题意, 说的是组合, 但其实求得是排列

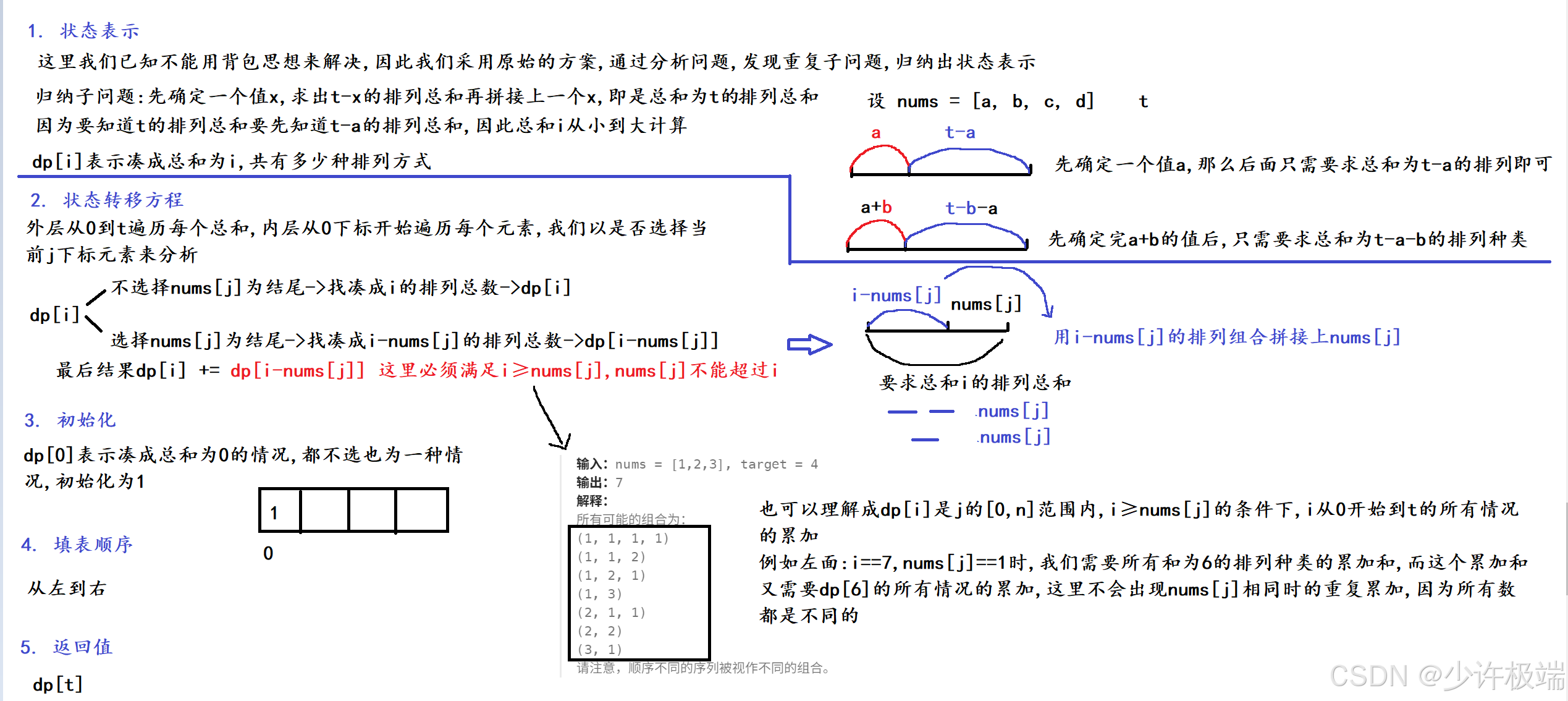
2. 算法原理

像背包问题, 但其实不是背包问题, 用原始的归纳来解决

3. 代码

java 复制代码

class Solution {
    public int combinationSum4(int[] nums, int target) {
        // 建表
        int n = nums.length;
        int[] dp = new int[target + 1];
        // 初始化
        dp[0] = 1;
        // 填表
        for (int i = 1; i <= target; i++) {
            for (int j = 0; j < n; j++) {
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        // 返回值
        return dp[target];
    }
}

四. (卡特兰数) 力扣 96. 不同的二叉搜索树

1. 题目解析

重点是理解什么是二叉搜索树

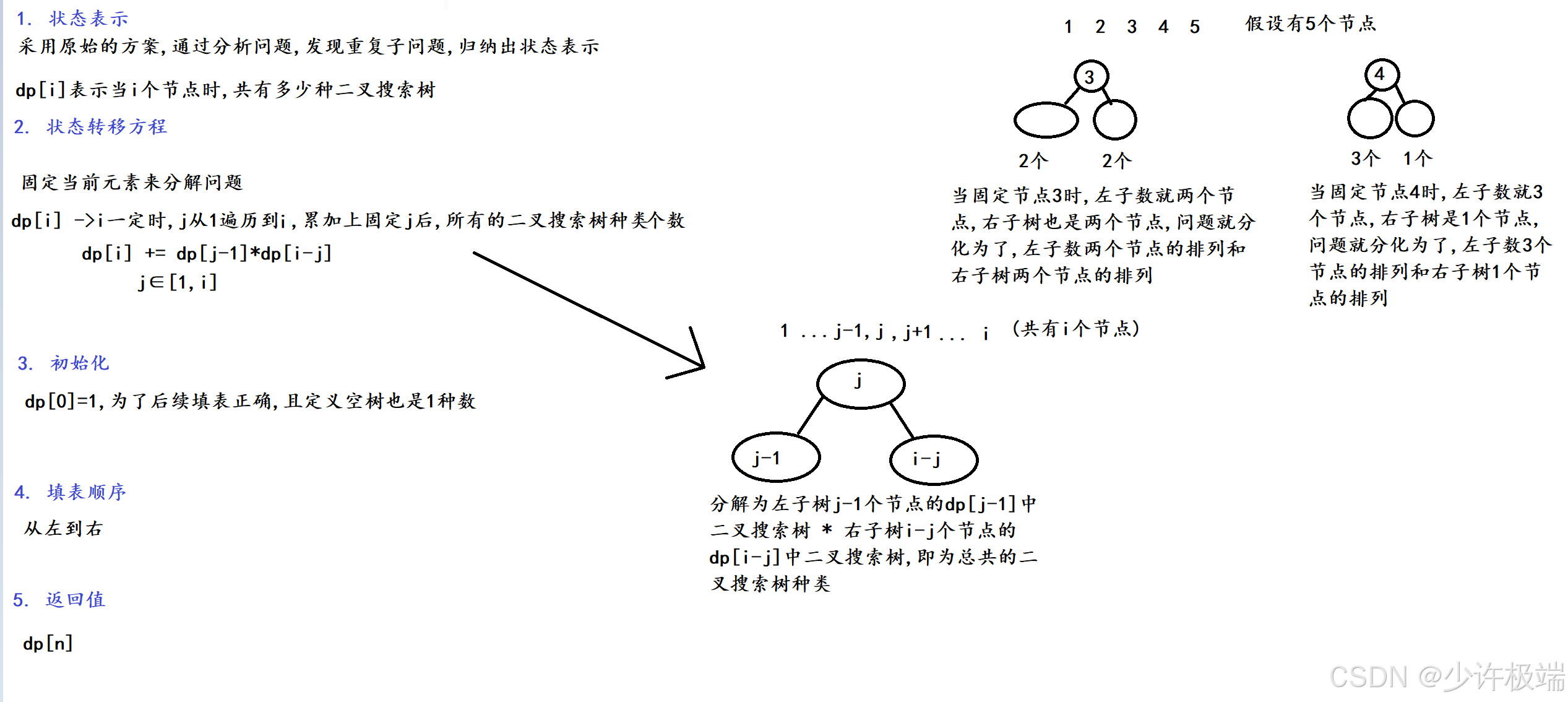
2. 算法原理

3. 代码

java 复制代码

class Solution {
    public int numTrees(int n) {
        // 建表
        int[] dp = new int[n + 1];
        // 初始化
        dp[0] = 1;
        // 填表
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        // 返回值
        return dp[n];
    }
}