[笔记]CDQ 分治

前

CDQ 分治 是一种分治算法，或者说是一种思想，其主要内容是：将序列通过递归的方式分给左右两个区间，每一个子问题只处理跨左右区间的贡献。

使用 CDQ 分治建立在排序的基础上，这也说明 CDQ 分治必须离线使用。

CDQ 分治可以解决的问题：

• 与点对有关的问题（数点 & 偏序）。
• 将带修改 & 查询的动态问题，转化为静态问题。
• 优化 1D / 1D 动态规划的转移。

本质上，这些问题都属于"点对之间的贡献问题"。

点对有关问题

一些概念

偏序

\(k\) 维偏序问题 ，即在一个由 \(n\) 个 \(k\) 元组构成的集合 \(\{(a_{1,1},\dots,a_{1,k}),\dots,(a_{n,1},\dots,a_{n,k})\}\) 中，求与 \((a_{i,1},\dots,a_{i,k})\) 满足某种偏序关系，即 \((a_{i,1},\dots,a_{i,k})\prec(a_{j,1},\dots,a_{j,k})\) 的 \(j\) 的个数。

这其中，"\(\prec\)" 是一种具有自反性、反对称性、传递性的二元关系，例如：

• 二维偏序 \((a,b)\) 中，\(a_i\le a_j,\ b_i<b_j\)
• 三维偏序 \((a,b,c)\) 中，\(a_i>a_j,\ b_i\le b_j,c_i\le c_j\)
• \(\dots\)

逆序对就是常见的二维偏序问题，此时这个集合可以写为 \(\{(1,a_1),\dots,(n,a_n)\}\)。

数点

\(k\) 维数点问题 ，即在一个由 \(n\) 个 \(k\) 元组构成的集合 \(\{(a_{1,1},\dots,a_{1,k}),\dots,(a_{n,1},\dots,a_{n,k})\}\) 中，求满足下列条件的 \(k\) 元组 \((a_{j,1},\dots,a_{j,k})\) 的个数 / 权值和：

• \(l_1\le a_{j,1}\le r_1\)
• \(\dots\)
• \(l_n\le a_{j,n}\le r_n\)

可以理解为在 \(k\) 维平面上给定若干点，查询某个区域内点的个数。

二维偏序

例 \(1\)：给定 \(n\) 个二元组，对每一组 \((x_i,y_i)\)，求满足 \(x_j<x_i,y_j<y_i\) 的 \(j\) 的个数（为了方便，我们假定 \(x\) 两两不同）。

比较暴力的方法就是枚举 \(i,j\) 并统计，这样子解决 \(k\) 维偏序的时间复杂度是 \(O(n^2k)\)。

我们有很多策略来优化这个时间复杂度，而这些策略有一个共同的思想 ------ 降维。

实现降维，我们有很多方式，例如：

• 排序
• 数据结构
• CDQ 分治

这些东西可以结合起来使用，每使用一个就会降掉一维。拿该问题举例：

• 排序 + 数据结构 ：先按 \(x\) 从小到大排序，然后依次遍历每一个 \(y_i\)，先查询树状数组中 \(<y_i\) 的个数，作为 \(i\) 的答案，再将 \(y_i\) 扔进树状数组。
• 数据结构 + 数据结构 ：树套树，外层维护 \(x\)，内层维护 \(y\)。
• 排序 + CDQ 分治：见下。

一般来说，排序仅能使用一次，放在最外层；而数据结构如果嵌套超过 \(1\) 层，就会带来较大的常数 & 空间消耗（例如树套树的空间一般是 \(O(n\log^2 n)\) 的，题目卡空间的话就没办法了）。因此应对更高维的偏序，可嵌套且时空常数小的 CDQ 分治是必不可少的。

CDQ 分治必须配合排序使用，为此我们先按 \(x\) 从小到大为这些二元组排序。

接下来我们从 \([1,n]\) 开始，逐层递归，分出子问题来求解。

具体来说，对于 \([l,r]\) 这个子问题：

• 令 \(mid\) 为 \(l,r\) 的中点。
• 递归地解决 \([l,mid],[mid+1,r]\)。
• 统计 \([l,mid]\) 对 \([mid+1,r]\) 的贡献。

其中第三步，我们可以将左右区间分别按 \(y\) 从小到大排序，并用双指针 \(i,j\) 分别指向 \(l\) 和 \(mid+1\)，即两个区间的开头。

尽管这样破坏了 \(x\) 的顺序，但由于是左右区间内部的排序，所以对于所有 \(i\in [l,mid],j\in [mid+1,r]\)，总有 \(x_i<x_j\)。

第一维的限制已经被开始时的排序解决掉了。

所以，我们仅需统计 \(y_i<y_j\) 的个数。这个用双指针扫一遍即可：

struct Node{int x,y,id;}a[N];
inline bool cmpx(Node& a,Node& b){return a.x<b.x;};
inline bool cmpy(Node& a,Node& b){return a.y<b.y;};
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j;
	cdq(l,mid),cdq(mid+1,r);
	sort(a+l,a+mid+1,cmpy),sort(a+mid+1,a+r+1,cmpy);
	for(i=l,j=mid+1;j<=r;j++){
		while(i<=mid&&a[i].y<a[j].y) i++;
		ans[a[j].id]+=i-l;
	}
}
//main
sort(a+1,a+1+n,cmpx);
cdq(1,n);

这样做时间复杂度是 \(O(n\log^2 n)\) 的。

一个常用的技巧是在递归的过程中进行 \(y\) 的归并排序，这样就优化为 \(O(n\log n)\) 了。

struct Node{int x,y,id;}a[N];
inline bool cmpx(Node& a,Node& b){return a.x<b.x;};
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		while(i<=mid&&a[i].y<a[j].y) t[k++]=a[i++];
		ans[a[j].id]+=i-l,t[k++]=a[j++];
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
//main
sort(a+1,a+1+n,cmpx);
cdq(1,n);

看上去有点熟悉？其实这就是归并排序求逆序对啦～

归并排序求逆序对在本质上可以看做 CDQ 分治的一个简单应用。

这样子先按 \(x\) 排序，再按 \(y\) 的顺序进行合并，我们称之为"对 \(x\) 分治，按照 \(y\) 合并"。

例 \(2\)：给定 \(n\) 个二元组，对每一组 \((x_i,y_i)\)，求满足 \(x_j\le x_i,y_j\le y_i\) 的 \(j\) 的个数。

思路是一样的，不过要注意两个细节问题：

• 从上面的代码，我们发现到 CDQ 分治始终是单向统计贡献（一般令左区间给右区间），双向的贡献无法用 CDQ 很好地维护。

  而在此题条件下，重复的元素会相互产生贡献。为此我们将原数组进行去重，并记录每个元素在原序列的出现次数。

• 另外由于 \(x\) 可能有重复元素，所以我们在主函数的排序过程中，\(x\) 相等时要再按 \(y\) 进行排序。否则可能有两个 \(x\) 相同的元素，\(y\) 小的被放在右区间，\(y\) 大的被放在左区间，这样前者永远无法为后者提供贡献，就错了。

int idx,w[N];//w记录去重后每个元素在原序列的出现次数
struct Node{int x,y,id;}a[N];
inline bool cmpx(Node& a,Node& b){return a.x==b.x?a.y<b.y:a.x<b.x;};
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,c=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		while(i<=mid&&a[i].y<=a[j].y) c+=w[a[i].id],t[k++]=a[i++];//记入贡献
		//1.注意条件是<=  2.加的不是1而是w
		ans[a[j].id]+=i-l,t[k++]=a[j++];//统计贡献
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
//main
sort(a+1,a+1+n,cmpx);
for(int i=1;i<=n;i++){//相同元素合并起来
	if(a[i].x==a[idx].x&&a[i].y==a[idx].y) w[idx]++;
	else a[++idx]=a[i],a[idx].id=idx,w[idx]=1;
}
for(int i=1;i<=idx;i++) ans[i]=w[i];
cdq(1,idx);

需要留心的是，在例 \(1\) 中，我们假定了 \(x\) 值互不相同。

如果存在相同的 \(x\)，就无法保证"左区间的 \(x\) \(<\) 右区间的 \(x\)"，因此不能完全套用上面的做法。

因为题目一般不会严苛到 \(k\) 个维度都限制"关系严格小于，且有重复元素"，所以这个问题基本不会遇到，我们可以先不管。

然而作为 CDQ 分治的一个 corner case，这样的小问题是不容忽视的，我们会在文章后的"细节" 部分讨论该问题的解决方法。

三维偏序

P3810 【模板】三维偏序（陌上花开）

给定 \(n\) 个三元组，记 \(f(i)\) 为满足 \(a_j\le a_i,b_j\le b_i,c_j\le c_i\) 且 \(j\ne i\) 的 \(j\) 的个数。

对于 \(d\in[0,n)\)，求满足 \(f(i)=d\) 的 \(i\) 的个数。

比较常见的做法：

• 排序 + 数据结构 + 数据结构：先通过排序将第一维离线，剩下就是二维偏序了，树套树即可解决。
• 排序 + CDQ 分治 + 数据结构：见下。
• 排序 + CDQ 分治 + 分治：见下。

排序 + CDQ 分治 + 数据结构

我们不妨对 \(a\) 分治，按 \(b\) 合并。

这样，在 \(j\) 指针统计贡献时，左区间内被记入的贡献已经满足了 \(a_i\le a_j,b_i\le b_j\)，怎么统计 \(c_i\le c_j\) 的 \(i\) 的个数呢？

很自然地想到用数据结构来维护。左指针 \(i\) 记入贡献时，在其上修改 \(c_i\) 处的值；右指针 \(j\) 统计贡献时，在其上查询 \(\le c_j\) 的总和即可。

所选的数据结构只需要支持单点修改、前缀查询，果断选择树状数组。毕竟常数才是制胜之法～

同样需要注意两个细节：

• 不要忘记去重～

• 主函数中要按 \(a,b,c\) 三个关键字排序，\(b,c\) 顺序无所谓。

  想一想，cdq 内部对 \(b\) 的排序时，如果 \(b\) 相等还需要按 \(c\) 排吗？

  这个是不需要的，因为 \(b\) 值相同时，无论 \(c\) 顺序如何，记入贡献总是在统计贡献之前，对答案不影响。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R229522693

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,V=2e5+10;
int n,k,w[N],f[N],idx,ans[N];
struct Node{int a,b,c,id;}a[N],t[N];
inline bool cmpa(Node& a,Node& b){return a.a==b.a?(a.b==b.b?a.c<b.c:a.b<b.b):a.a<b.a;}
inline int lb(int x){return x&-x;}
struct BIT{
	int s[V];
	inline void chp(int x,int v){for(;x<=k;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=k;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	//注意clr不能单独使用，因为经过的位置全部置为0会破坏树状数组的性质（另外这个小优化亲测是有效果的）
	inline int query(int x){int ans=0;for(;x;x-=lb(x)) ans+=s[x];return ans;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		while(i<=mid&&a[i].b<=a[j].b) bit.chp(a[i].c,w[a[i].id]),t[k++]=a[i++];
		f[a[j].id]+=bit.query(a[j].c),t[k++]=a[j];
	}
	for(j=l;j<i;j++) bit.clr(a[j].c);//记得清空
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b>>a[i].c;
	sort(a+1,a+1+n,cmpa);
	for(int i=1;i<=n;i++){
		if(a[i].a==a[idx].a&&a[i].b==a[idx].b&&a[i].c==a[idx].c) w[idx]++;
		else a[++idx]=a[i],a[idx].id=idx,w[idx]=1;
	}
	cdq(1,idx);
	for(int i=1;i<=idx;i++) ans[f[a[i].id]+w[a[i].id]-1]+=w[a[i].id];
	//这里注意，需要额外统计w-1的贡献
	for(int i=0;i<n;i++) cout<<ans[i]<<"\n";
	return 0;
}

排序 + CDQ 分治 + CDQ 分治

就效率来说，CDQ 分治的确比不过常数更小的树状数组。

我们在这里用两层 CDQ 分治来解决，是为了展示 CDQ 分治的可嵌套性，并且为接下来的四维偏序做个铺垫。

回顾我们刚才分治的思路。在对 \(a\) 分治的过程中，每一个子问题将其管辖的 \(a\) 归为两类，左区间编号为 \(L_a\)，右区间编号为 \(R_a\)。按 \(b\) 合并的过程中，我们规定只有 \((L_a,b,c)\) 能对 \((R_a,b,c)\) 产生贡献。

放在这个做法，如果一个子问题的 \(a\) 已经被分类为了 \(L_a,R_a\)，我们就对这些三元组再按 \(b\) 排序，左区间编号为 \(L_b\)，右区间编号为 \(R_b\)。在按 \(c\) 合并的过程中，我们规定只有 \((L_a,L_b,c)\) 能对 \((R_a,R_b,c)\) 产生贡献。

总结一下实现步骤：

• 第一层 CDQ 按 \(a\) 分治，按 \(b\) 合并，并编号 \(L_a,R_a\)，将编号记录在结构体数组中。
• 第二层 CDQ 按 \(b\) 分治，按 \(c\) 合并，此时左区间是 \(L_b\)，右区间是 \(R_b\)。计算贡献时，额外限制只有带 \(L_a\) 编号的 \(i\) 能记入贡献；带 \(R_a\) 编号的 \(j\) 能统计贡献。

实现细节：

• 注意去重。

• 主函数中要按 \(a,b,c\) 三个关键字排序，\(b,c\) 顺序无所谓。

  cdq2d 中要按 \(b,c,a\) 三个关键字排序，\(a,c\) 顺序无所谓。之所以要顾及 \(a,c\)，是因为 cdq3d 中我们要用到 \(a\) 所属的编号以及 \(c\)。与之前同理，我们同样要让可能计入贡献的元素尽可能放在左边。

  stable_sort 是稳定排序，能保证在自定义的排序规则下，相等的元素在排序后相对顺序不变 。因此，如果你使用 stable_sort，那么 cmp 函数就仅需比较 \(b\) 了。

  stable_sort 的底层实现是归并排序。这也是为什么如果你在 CDQ 的过程中进行归并排序，同样只需比较当前合并的属性。

  有关 sort 和 stable_sort 的使用，我们会在"细节" 部分进一步讨论。

  cdq3d 中按 \(c\) 排序即可。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R229537875

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,V=2e5+10;
int n,k,w[N],f[N],idx,ans[N];
struct Node{int a,b,c,id;bool s;}a[N],t2d[N],t3d[N];//s=0/1 对应 Lx/Rx
inline bool cmpa(Node& a,Node& b){return a.a==b.a?(a.b==b.b?a.c<b.c:a.b<b.b):a.a<b.a;}
void cdq3d(int l,int r){//按第3维合并
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,c=0;
	cdq3d(l,mid),cdq3d(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		while(i<=mid&&t2d[i].c<=t2d[j].c){
			if(!t2d[i].s) c+=w[t2d[i].id];//Lx,Ly才能记入贡献
			t3d[k++]=t2d[i++];
		}
		if(t2d[j].s) f[t2d[j].id]+=c;//Rx,Ry才能统计贡献
		t3d[k++]=t2d[j];
	}
	while(i<=mid) t3d[k++]=t2d[i++];
	for(i=l;i<=r;i++) t2d[i]=t3d[i];
}
void cdq2d(int l,int r){//按第2维合并
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq2d(l,mid),cdq2d(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){//仅为x编号，不统计贡献
		while(i<=mid&&a[i].b<=a[j].b) a[i].s=0,t2d[k++]=a[i++];
		a[j].s=1,t2d[k++]=a[j++];
	}
	while(i<=mid) a[i].s=0,t2d[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t2d[i];
	cdq3d(l,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b>>a[i].c;
	sort(a+1,a+1+n,cmpa);
	for(int i=1;i<=n;i++){
		if(a[i].a==a[idx].a&&a[i].b==a[idx].b&&a[i].c==a[idx].c) w[idx]++;
		else a[++idx]=a[i],a[idx].id=idx,w[idx]=1;
	}
	cdq2d(1,idx);
	for(int i=1;i<=idx;i++) ans[f[a[i].id]+w[a[i].id]-1]+=w[a[i].id];
	for(int i=0;i<n;i++) cout<<ans[i]<<"\n";
	return 0;
}

经过测试，三种方法的用时分别为：1090ms、320ms、700ms。

四维偏序

U322249 【模板】四维偏序

理论上 CDQ 是可以无限嵌套的，你可以照上面的分析写三重 CDQ 来实现。

不过我们这里只提一种，也是最常用、效率相对较高的。

排序 + CDQ 分治 + CDQ 分治 + 数据结构

将三维偏序的两个方法结合一下，有了前面的铺垫应该不难理解。

实现步骤：

• 第一层 CDQ 按 \(a\) 分治，按 \(b\) 合并，并编号 \(L_a,R_a\)，将编号记录在结构体数组中。
• 第二层 CDQ 按 \(b\) 分治，按 \(c\) 合并，此时左区间是 \(L_b\)，右区间是 \(R_b\)。计算贡献时，对于带 \(L_a\) 编号的 \(i\)，将 \(d_i\) 加入树状数组；对于带 \(R_a\) 编号的 \(j\)，在树状数组上查询 \(\le d_j\) 的元素个数，并统入 \(j\) 的答案。

实现细节与上面相同，额外注意树状数组维护的那一维要离散化。

时间复杂度 \(O(n\log^3 n)\)。
点击查看代码 - R229587835

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
const int N=1e5+10;
struct Node{int d1,d2,d3,d4,id;bool s;}a[N],t2d[N],t3d[N];
inline bool cmp(Node& a,Node& b){return a.d1==b.d1?(a.d2==b.d2?(a.d3==b.d3?a.d4<b.d4:a.d3<b.d3):a.d2<b.d2):a.d1<b.d1;}
gp_hash_table<int,int> ma;//起到和umap相同的作用，效率一般更高
int n,k,tn,b[N],idx,w[N],f[N],ans[N];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=tn;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=tn;x+=lb(x)) if(!s[x]) break;else s[x]=0;}
	inline int query(int x){int ans=0;for(;x;x-=lb(x)) ans+=s[x];return ans;}
}bit;
void cdq3d(int l,int r){//按第3维合并
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq3d(l,mid),cdq3d(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		while(i<=mid&&t2d[i].d3<=t2d[j].d3){
			if(!t2d[i].s) bit.chp(t2d[i].d4,w[t2d[i].id]);
			t3d[k++]=t2d[i++];
		}
		if(t2d[j].s) f[t2d[j].id]+=bit.query(t2d[j].d4);
		t3d[k++]=t2d[j];
	}
	for(j=l;j<i;j++) if(!t2d[j].s) bit.clr(t2d[j].d4);
	while(i<=mid) t3d[k++]=t2d[i++];
	for(i=l;i<=r;i++) t2d[i]=t3d[i];
}
void cdq2d(int l,int r){//按第2维合并
	if(l==r) return;
	int mid=(l+r)>>1,i,j,s;
	cdq2d(l,mid),cdq2d(mid+1,r);
	for(i=s=l,j=mid+1;j<=r;j++){
		while(i<=mid&&a[i].d2<=a[j].d2) a[i].s=0,t2d[s++]=a[i++];
		a[j].s=1,t2d[s++]=a[j];
	}
	while(i<=mid) a[i].s=0,t2d[s++]=a[i++];
	for(int i=l;i<=r;i++) a[i]=t2d[i];
	cdq3d(l,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i].d1>>a[i].d2>>a[i].d3>>a[i].d4,b[i]=a[i].d4;
	sort(b+1,b+1+n),tn=unique(b+1,b+1+n)-b-1;
	for(int i=1;i<=tn;i++) ma[b[i]]=i;
	sort(a+1,a+1+n,cmp);
	for(int i=1;i<=n;i++){
		if(a[i].d1==a[idx].d1&&a[i].d2==a[idx].d2&&a[i].d3==a[idx].d3&&a[i].d4==a[idx].d4) w[idx]++;
		else a[++idx]=a[i],a[idx].id=idx,w[idx]=1;
	}
	for(int i=1;i<=idx;i++) a[i].d4=ma[a[i].d4];
	cdq2d(1,idx);
	for(int i=1;i<=idx;i++) ans[f[a[i].id]+w[a[i].id]-1]+=w[a[i].id];
	for(int i=0;i<n;i++) cout<<ans[i]<<"\n";
	return 0;
}

CDQ 嵌套，理论可以做任意维的偏序。

不过常数也会随嵌套而累乘，面对很高维的偏序，CDQ 分治甚至可能劣于 \(O(n^2k)\) 的暴力（并未实测）。

题外话：如果维数超过 \(5\)，我们一般会采用 bitset 优化的暴力，可达到 \(O(\frac{1}{\omega}n^2)\) 的时间复杂度，其中 \(\omega=32\)（计算机的位数）。

数点

\(k\) 维偏序本质上是在处理 \(k\) 维的前缀查询。

我们通过差分，将原查询拆成若干个（\(2^k\) 个）前缀查询即可，为每个元素添加 c 属性，值为 \(\pm1\)，表示对答案的累加 / 累减。

偏序问题每个元素，既是一个修改，也是一个查询。意味着一个元素既可以计入贡献，又可以统计贡献，取决于其所在的区间。

而数点问题将查询独立出来了，也就是说只有左区间的修改操作 能计入贡献，右区间的查询操作能统计贡献。加粗的部分需要额外限制一下。

例题

P2163 [SHOI2007] 园丁的烦恼

二维数点模板题。

思路就是二维差分，将矩形 \((x_1,y_1,x_2,y_2)\) 拆成四个前缀的查询：

• 加上 \((x_2,y_2)\)
• 减去 \((x_1-1,y_2)\)
• 减去 \((x_2,y_1-1)\)
• 加上 \((x_1-1,y_1-1)\)

时间复杂度 \(O((n+m)\log(n+m))\)。
点击查看代码 - R229760252

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=5e5+10;
struct Node{int id,x,y,c,k;}a[N+4*M],t[N+4*M];//c=1/-1 表示累加/累减，k=0/1 表示修改/查询
inline bool cmpx(Node& a,Node& b){return a.x==b.x?a.id<b.id:a.x<b.x;}
int n,m,idx,ans[M];
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,s=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[i].y<=a[j].y;i++){
			s+=a[i].k;
			t[k++]=a[i];
		}
		ans[a[j].id]+=a[j].c*s;
		t[k++]=a[j];
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m,idx=n;
	for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y,a[i].k=1;
	for(int i=1,x,y,xx,yy;i<=m;i++){
		cin>>x>>y>>xx>>yy;//一个询问拆成4个
		a[++idx]={i,xx,yy,1,0};
		a[++idx]={i,xx,y-1,-1,0};
		a[++idx]={i,x-1,yy,-1,0};
		a[++idx]={i,x-1,y-1,1,0};
	}
	sort(a+1,a+1+idx,cmpx);
	cdq(1,idx);
	for(int i=1;i<=m;i++) cout<<ans[i]<<"\n";
	return 0;
}

P8575 「DTOI-2」星之河

将点用 DFS 序重新编号，这样"\(i\) 在 \(j\) 子树中" 的条件就转化为"\(dfn_i\in [dfn_j,dfn_j+siz_j-1]\)"。

再加上 \(\text{Red,Blue}\) 两个属性，就是超级板子的三维数点了。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R229316575

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,head[N],idx,tim,dfn[N],ans[N];
struct Edge{int nxt,to;}e[N<<1];
struct Node{int l,r,a,b;}a[N],t[N];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
inline bool cmpa(Node& a,Node& b){return a.a==b.a?a.b==b.b?a.l>b.l:a.b<b.b:a.a<b.a;}
inline void add(int u,int v){e[++idx]={head[u],v},head[u]=idx;}
void dfs(int u,int fa){
	a[u].l=dfn[u]=++tim;
	for(int i=head[u],v;i;i=e[i].nxt) if((v=e[i].to)!=fa) dfs(v,u);
	a[u].r=tim;
}
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&a[i].b<=a[j].b;){
			bit.chp(a[i].l,1);
			t[k++]=a[i++];
		}
		ans[a[j].l]+=bit.qry(a[j].r)-bit.qry(a[j].l);
		t[k++]=a[j++];
	}
	for(j=l;j<i;j++) bit.clr(a[j].l);
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1,u,v;i<n;i++) cin>>u>>v,add(u,v),add(v,u);
	for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b;
	dfs(1,0);
	sort(a+1,a+1+n,cmpa);
	cdq(1,n);
	for(int i=1;i<=n;i++) if(ans[dfn[i]]) cout<<ans[dfn[i]]<<"\n";
	return 0;
}

CF1311F Moving Points

不难发现，\(i,j\) 两点对答案有贡献，当且仅当 \(x_i<x_j,v_i\le v_j\)，此时贡献为 \(x_j-x_i\)。

这样就是二维偏序问题，统计时向答案累加 \((i-l)\times x_j-s\)，其中 \(s=\sum\limits_{i=l}^{i-1} x_i\)。
点击查看代码 - #332472535

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
struct Node{int x,v;}a[N],t[N];
bool cmp(Node& a,Node& b){return a.x==b.x?a.v<b.v:a.x<b.x;}
int n,ans;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,sum=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&a[i].v<=a[j].v;) sum+=a[i].x,t[k++]=a[i++];
		ans+=(i-l)*a[j].x-sum,t[k++]=a[j++];
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].x;
	for(int i=1;i<=n;i++) cin>>a[i].v;
	sort(a+1,a+1+n,cmp);
	cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

P5459 [BJOI2016] 回转寿司

题意就是统计有多少个 \([l,r]\) 使得 \(\sum\limits_{i=l}^r a_i\in [L,R]\)。

令 \(s\) 为 \(a\) 的前缀和数组，我们要找的就是满足下列条件的 \((i,j)\) 个数：

• \(id_i<id_j\)
• \(s_j-s_i\in[L,R]\)。

\(s\) 的限制是一个区间，不能放在最外层排序。因此我们对 \(id\) 分治，并按 \(s\) 合并。

\(s\) 的限制可以在合并时使用差分，即将指针 \(i\) 拆成两个 \(i_1,i_2\)，分别记录 \(s_j-s_i\ge L\) 和 \(s_j-s_i>R\) 的贡献，两个 \(i\) 的贡献作差即可。

由于 \(i\) 和 \(s_i\) 初始均有序，所以不需要进行任何排序。

时间复杂度 \(O(n\log n)\)。
点击查看代码 - R231273824

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10;
int n,L,R,a[N],ans,t[N];
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i1,i2,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=i1=i2=k=l,j=mid+1;j<=r;){
		while(i1<=mid&&a[j]-a[i1]>=L) i1++;
		while(i2<=mid&&a[j]-a[i2]>R) i2++;
		while(i<=mid&&a[i]<=a[j]) t[k++]=a[i++];
		ans+=i1-i2,t[k++]=a[j++];
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	cin>>n>>L>>R;
	for(int i=1;i<=n;i++) cin>>a[i],a[i]+=a[i-1];
	cdq(0,n);
	cout<<ans<<"\n";
	return 0;
}

P1972 [SDOI2009] HH 的项链

区间数颜色，我们有一个很标准的技巧。

令 \(pre_i\) 为 \(a_i\) 上一次出现的位置，若不存在则为 \(0\)。

则找 \([l,r]\) 内有多少种颜色，等价于统计满足下列条件的 \(j\) 的个数：

• \(j\in [l,r]\)
• \(pre_j\in [0,l)\)

这就转化成二维数点了。

由于 \(pre\) 的询问已经是一个前缀，所以一个查询拆成俩就可以。

时间复杂度 \(O((n+m)\log (n+m))\)。
点击查看代码 - R230545952

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=1e6+10;
struct Node{int d1,d2,d3,c;}a[N+2*M],t[N+2*M];//两个操作：(0,lst_i,i,0)、(i,limit_lst,limit_i,统计时的权重)
bool cmp(Node& a,Node &b){return a.d2==b.d2?a.d3==b.d3?a.d1<b.d1:a.d3<b.d3:a.d2<b.d2;}
unordered_map<int,int> lst;
int n,m,idx,ans[M];
inline int lb(int x){return x&-x;}
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,c=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&a[i].d3<=a[j].d3;){
			if(!a[i].d1) c++;
			t[k++]=a[i++];
		}
		if(a[j].d1) ans[a[j].d1]+=c*a[j].c;
		t[k++]=a[j++];
	}
	for(;i<=mid;) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n,idx=n;
	for(int i=1,x;i<=n;i++) cin>>x,a[i].d2=lst[x],lst[x]=a[i].d3=i;
	cin>>m;
	for(int i=1,l,r;i<=m;i++) cin>>l>>r,a[++idx]={i,l-1,r,1},a[++idx]={i,l-1,l-1,-1};
	sort(a+1,a+1+idx,cmp),cdq(1,idx);
	for(int i=1;i<=m;i++) cout<<ans[i]<<"\n";
	return 0;
}

另解

我们之所以要将询问拆分，是因为分治和排序仅能处理一个前缀。不过树状数组等数据结构，本身就支持一个区间的查询。

因此，我尝试在 CDQ 的基础上嵌套了一层树状数组，来维护下标的区间查询，这样有两个好处：

• 无需拆分询问，操作总数从 \(n+2m\) 变成了 \(n+m\)。
• 节点不需要再记录 c（统计倍率）属性，减少了转移负担。

虽然理论复杂度会添一只 \(\log n\)，但是实测居然跑得更快一些（12.18s \(\rightarrow\) 11.53s）。
点击查看代码 - R230552064

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=1e6+10;
struct Node{int d1,d2,d3;}a[N+M],t[N+M];//两个操作：(0,lst_i,i)、(i,l_i,r_i)
unordered_map<int,int> lst;
int n,m,idx,ans[M];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,s;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=s=l,j=mid+1;j<=r;){
		for(;s<=mid&&a[s].d2<=a[j].d2-1;s++) if(!a[s].d1) bit.chp(a[s].d3,1);
		for(;i<=mid&&a[i].d2<=a[j].d2;) t[k++]=a[i++];
		if(a[j].d1) ans[a[j].d1]+=bit.qry(a[j].d3)-bit.qry(a[j].d2-1);
		t[k++]=a[j++];
	}
	for(j=l;j<i;j++) bit.clr(a[j].d3);
	for(;i<=mid;) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n,idx=n;
	for(int i=1,x;i<=n;i++) cin>>x,a[i].d2=lst[x],lst[x]=a[i].d3=i;
	cin>>m;
	for(int i=1,l,r;i<=m;i++) cin>>l>>r,a[++idx]={i,l,r};
	cdq(1,idx);
	for(int i=1;i<=m;i++) cout<<ans[i]<<"\n";
	return 0;
}

[P11197 [COTS 2021] 赛狗游戏 Tiket](P11197 [COTS 2021] 赛狗游戏 Tiket)

令 \(i\) 在 \(T,A,B,C\) 中出现的位置分别为 \(p_i,a_i,b_i,c_i\)，则 \((i,j)\) 产生贡献条件很容易写：

• \(p_i<p_j\land a_i<a_j\land b_i<b_j\land c_i<c_j\) 或者
• \(p_i>p_j\land a_i<a_j\land b_i<b_j\land c_i<c_j\)

看起来是四维偏序？可如果你写四维偏序，可能会像我一样 TLE 36pts。

其实我们不难发现 \(p_i<p_j,p_i>p_j\) 一定恰有一式成立。

所以 \(p\) 的限制相当于没有。

题意转化为求 \(a_i<a_j\land b_i<b_j\land c_i<c_j\) 的 \((i,j)\) 数量，三维偏序板子。
点击查看代码 - R231691122

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10;
struct Node{int a,b,c;}a[N],t[N];
int n,ans;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&a[i].b<a[j].b;){
			bit.chp(a[i].c,1);
			t[k++]=a[i++];
		}
		ans+=bit.qry(a[j].c-1);
		t[k++]=a[j++];
	}
	for(j=l;j<i;j++) bit.clr(a[j].c);
	for(;i<=mid;) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1,x;i<=n;i++) cin>>x;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].a=i;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].b=i;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].c=i;
	sort(a+1,a+1+n,[](Node& a,Node& b){return a.a<b.a;});
	cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

P5094 [USACO04OPEN] MooFest G 加强版

题目给我们的式子带 \(\max\) 还带绝对值，考虑将其简化。

其中 \(\max\)，我们对 \(v\) 排个序就解决了。

而与 \(x\) 相关的绝对值，我们一般有两种对策：

• 将 \(x\) 扔到树状数组上处理。
• 按 \(x\) 合并的同时处理。

因为这道题只有两维，所以两种方法其实就是排序 + 数据结构 和 排序 + CDQ 分治。

排序 + 数据结构

这个可能相对好想一些。

将二元组 \((x,v)\) 按 \(v\) 从小到大排序，依次遍历每个二元组，对于 \((x_j,v_j)\)：

1. 将满足 \(i<j,x_i<x_j\) 的 \(i\) 的个数记为 \(c\)，这些 \(x_i\) 的总和记为 \(s\)。

   对答案产生 \((c\times x_j-s)\times v_j\) 的贡献。

2. 将满足 \(i<j,x_i>x_j\) 的 \(i\) 的个数记为 \(c\)，这些 \(x_i\) 的总和记为 \(s\)。

   对答案产生 \((s-c\times x_j)\times v_j\) 的贡献。

点击查看代码 - R227554505

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,Ve=5e4,V=Ve+10;//e=exact
int n,ans;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[V],c[V];
	void chp(int x,int v){for(;x<=Ve;x+=lb(x)) s[x]+=v,c[x]++;}
	void qry(int x,int y,int& _s,int& _c){
		_s=_c=0,x--;
		for(;y;y-=lb(y)) _s+=s[y],_c+=c[y];
		for(;x;x-=lb(x)) _s-=s[x],_c-=c[x];
	}
}bit;
struct Node{int a,v;}a[N];
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].v>>a[i].a;
	sort(a+1,a+1+n,[](Node a,Node b){return a.v<b.v;});
	for(int i=1,s,c;i<=n;i++){
		bit.qry(1,a[i].a-1,s,c);
		ans+=a[i].v*(c*a[i].a-s);
		bit.qry(a[i].a+1,Ve,s,c);
		ans+=a[i].v*(s-c*a[i].a);
		bit.chp(a[i].a,a[i].a);
	}
	cout<<ans<<"\n";
	return 0;
}

排序 + CDQ 分治

我们按 \(v\) 从大到小的排序分治，这样就恒有 \(v_j\ge v_i\)，\(\max\) 始终落在 \(v_j\)。

按 \(x\) 合并。

对于某一时刻的 \(j\) 指针，假定 \(i\) 已经跑完了 while 循环。

那么此时 \([l,i)\) 内的 \(x\) 值全部 \(<x_j\)，\([i,mid]\) 内的 \(x\) 值全部 \(\ge x_j\)。

这样就可以拆掉绝对值了，此时对答案的贡献是：

\[v_i\times\big[(i-l)\times x_j-(\sum\limits_{k=l}^{i-1} x_k)+(\sum\limits_{k=i}^{mid} x_k)-(mid+1-i)\times x_j\big] \]

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R227561662

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10;
int n,ans;
struct Node{int a,v;}a[N],t[N];
int cdq(int l,int r){//返回值为[l,r]内a的和
	if(l==r) return a[l].a;
	int mid=(l+r)>>1,i,j,k,s=0,ss=cdq(l,mid),tmp=cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		while(i<=mid&&a[i].a<a[j].a) s+=a[i].a,t[k++]=a[i++];
		ans+=a[j].v*(((i-l)*a[j].a-s)+((ss-s)-(mid+1-i)*a[j].a));
		t[k++]=a[j];
	}
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
	return ss+tmp;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].v>>a[i].a;
	sort(a+1,a+1+n,[](Node& a,Node& b){return a.v<b.v;});
	cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

P3658 [USACO17FEB] Why Did the Cow Cross the Road III P

令 \(a_i\) 为 \(i\) 在左侧的出现位置，\(b_i\) 为 \(i\) 在右侧的出现位置。

\(i\) 对 \(j\) 产生贡献，当且仅当：

• \(a_i<a_j\)

• \(b_i>b_j\)

• \(|id_i-id_j|>K\)

  即 \(id_i>id_j+K\) 或 \(id_i<id_j-K\)

从上一题我们知道，处理绝对值大致有两种方法。

这里两种做法都是可用的，即：

• 按 \(a\) 分治，按 \(b\) 合并，树状数组维护 \(id\)。
• 按 \(a\) 分治，按 \(id\) 合并，树状数组维护 \(b\)。

提一嘴第二种写法。

我们的限制条件是 \(id_i>id_j+K\) 或 \(id_i<id_j-K\)，而 \(K\) 是一个常数。所以随着 \(j\) 的增加，限制 \(id_i\) 的两个端点也是单调不降的。这就可以用双指针来差分一下，具体见代码。

假如 \(K\) 不是常数，那么两个端点就未必单调移动，此时就只能使用第一种写法，将 \(id\) 放在树状数组上维护。

时间复杂度 \(O(n\log^2 n)\)，后者可能常数大一些，码起来也稍微绕一点。
实现 1 - R227870178

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct Data{int id,a,b;}a[N],t[N];
inline bool cmp(Data& a,Data& b){return a.a<b.a;}
int n,kk,ans;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
	inline int qry(int x,int y){return x>y?0:qry(y)-qry(x-1);}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[i].b>a[j].b;i++) bit.chp(a[i].id,1),t[k++]=a[i];
		ans+=bit.qry(a[j].id+kk+1,n)+bit.qry(1,a[j].id-kk-1),t[k++]=a[j];
	}
	for(j=l;j<i;j++) bit.clr(a[j].id);
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>kk;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].a=a[i].id=i;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].b=i;
	sort(a+1,a+1+n,cmp),cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

实现 2 - R229753185

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct Data{int id,a,b;}a[N],t[N];
inline bool cmp(Data& a,Data& b){return a.a>b.a;}//a从大到小排序
int n,kk,ans;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,L,R;
	cdq(l,mid),cdq(mid+1,r);
	for(i=l;i<=mid;i++) bit.chp(a[i].b,1);//初始所有b都加入，随后双指针剔除id在[id_j-K,id_j+K]内的b
	for(i=k=L=R=l,j=mid+1;j<=r;){
		for(;R<=mid&&a[R].id<=a[j].id+kk;) bit.chp(a[R++].b,-1);
		for(;L<=mid&&a[L].id<a[j].id-kk;) bit.chp(a[L++].b,1);
		for(;i<=mid&&a[i].id<a[j].id;) t[k++]=a[i++];
		ans+=bit.qry(a[j].b),t[k++]=a[j++];
	}
	for(j=l;j<=mid;j++) bit.clr(a[j].b);
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>kk;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].a=a[i].id=i;
	for(int i=1,x;i<=n;i++) cin>>x,a[x].b=i;
	sort(a+1,a+1+n,cmp),cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

CF1045G AI robots

相当于给定 \(n\) 个三元组 \((x_i,r_i,q_i)\)，统计满足"能互相看见" 且"智商差距 \(\le K\)" 的点对数量。

其中"能互相看见" 的条件写成式子十分复杂，既带 \(\min\) 又有绝对值，因此首先考虑将它简化。

按之前的套路，我们先按视野 \(r\) 从大到小的排序分治。这样就恒有 \(r_j\le r_i\)，\(\min\) 始终落在 \(r_j\)。

这样"能互相看见" 的条件被简化为 \(|x_i-x_j|\le r_j\)，即 \(x_i\in [x_j-r_j,x_j+r_j]\)。

我们发现，随着 \(j\) 的增加，限制 \(x_i\) 的两个端点并不单调变化，不能简单地用双指针解决掉，必须按 \(q\) 合并，而将 \(x\) 扔到树状数组里维护。这样每个 \(j\) 我们仅需在树状数组上查询 \(x_i\in[x_j-r_j,x_j+r_j]\) 的个数就好了。

最后只剩下"智商差距 \(\le K\)"，即 \(|q_i-q_j|\le K\)，也即 \(q_i\in [q_j-K,q_j+K]\)。

这个式子与 \(K\) 有关，而 \(K\) 是一个常数。所以随着 \(j\) 的增加，左右端点是单调变化的，正好可以按 \(q\) 合并，使用双指针差分来解决。即 \(q_i\le q_j+K\) 的答案，再减去 \(q_i \le q_j-K-1\) 的答案。

所以总体思路是按 \(r\) 分治，按 \(q\) 合并，\(x\) 扔到树状数组上维护。

思路很巧妙的一道题，感觉就像为 CDQ 而设计的一样（不过 cf 题解给的是线段树，时空复杂度分别是 \(O(Kn\log n),O(n\log n)\)）。

代码离散化用到了 gp_hash_table，然而交上去 TLE on #13，说明 cf 卡这个了，因此借用了此文 by week_end 中的自定义哈希函数。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - #332029170

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define int long long
using namespace std;
using namespace __gnu_pbds;
const int N=1e5+10;
int n,kk,ans,b[3*N],tn;
struct Node{int x,r,q,lp,rp;}a[N],t[N];
inline bool cmpr(Node a,Node b){return a.r==b.r?(a.q==b.q?a.x<b.x:a.q<b.q):a.r>b.r;}
struct custom_hash{
	static uint64_t splitmix64(uint64_t x){
		x+=0x9e3779b97f4a7c15;
		x=(x^(x>>30))*0xbf58476d1ce4e5b9;
		x=(x^(x>>27))*0x94d049bb133111eb;
		return x^(x>>31);
	}
	size_t operator()(uint64_t x) const {
		static const uint64_t FIXED_RANDOM=chrono::steady_clock::now().time_since_epoch().count();
		return splitmix64(x+FIXED_RANDOM);
	}
};
gp_hash_table<int,int,custom_hash> ma;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[3*N];
	void chp(int x,int v){for(;x<=tn;x+=lb(x)) s[x]+=v;}
	void clr(int x){for(;x<=tn;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
	int qry(int x,int y){return qry(y)-qry(x-1);}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,L,R,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(L=R=i=k=l,j=mid+1;j<=r;j++){
		for(;R<=mid&&a[R].q-a[j].q<=kk;R++) bit.chp(a[R].x,1);
		for(;L<=mid&&a[L].q-a[j].q<-kk;L++) bit.chp(a[L].x,-1);
		for(;i<=mid&&a[i].q<=a[j].q;i++) t[k++]=a[i];
		ans+=bit.qry(a[j].lp,a[j].rp),t[k++]=a[j];
	}
	for(j=L;j<R;j++) bit.clr(a[j].x);
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>kk;
	for(int i=1;i<=n;i++){
		cin>>a[i].x>>a[i].r>>a[i].q;
		b[++tn]=a[i].x;
		b[++tn]=a[i].lp=a[i].x-a[i].r;
		b[++tn]=a[i].rp=a[i].x+a[i].r;
	}
	sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
	for(int i=1;i<=tn;i++) ma[b[i]]=i;
	for(int i=1;i<=n;i++) a[i].x=ma[a[i].x],a[i].lp=ma[a[i].lp],a[i].rp=ma[a[i].rp];
	sort(a+1,a+1+n,cmpr),cdq(1,n);
	cout<<ans<<"\n";
	return 0;
}

动态转静态

所谓动态转静态，本质上就是为所有操作额外加了一个属性 ------ 时间戳 \(tim\)。

\(i\) 能对 \(j\) 产生贡献，当且仅当：

• \(tim_i<tim_j\)
• \(i\) 是修改操作
• \(j\) 是查询操作
• ......（更多限制 依题目而定）

动态问题，本质上是在静态问题的基础上添加了 \(tim\) 这一维。

对输入的操作序列离线后，\(tim\) 是天然不降的。所以我们一般采用对 \(tim\)，也就是时间轴分治的策略。

需要注意的一点是，若询问之间相互独立 ，那么我们无需处理"左区间内部贡献""右区间内部贡献""跨区间贡献" 之间的时序关系。比如说 \(tim_i<tim_j<tim_k\)，\(i,j\) 两个单点加操作都对查询 \(k\) 有贡献，那么处理 \(i,j\) 的时间是随意的。

然而如果是单点赋值这样有时序依赖关系 的操作，我们就必须先处理 \(i\) 的贡献，再处理 \(j\) 的贡献。放在代码实现中，我们必须对时间轴分治，且分治时要先调用 cdq(l,mid)，再统计跨区间贡献，最后调用 cdq(mid+1,r)。

这样相当于对 CDQ 的递归树做中序遍历。可以发现，为某个节点提供贡献的点一定是按时间单调的，所以正确性可以保证。

如下图，绿色部分是要统计贡献的点，橙色部分是所有为其提供贡献的子问题（很像线段树上拆成的 \(O(\log n)\) 个区间），必须依照标号的顺序来提供贡献。

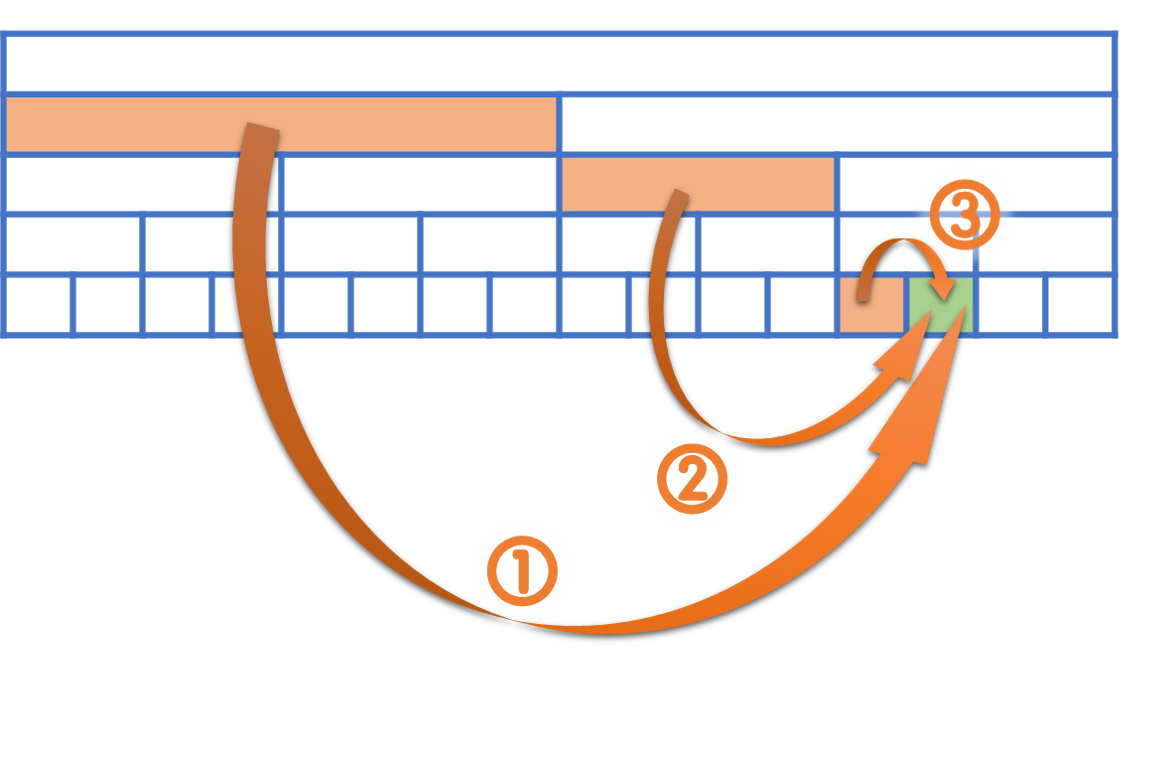
不过中序遍历会破坏归并排序的结构，使得我们写归并比较困难。因此为了降低代码复杂度，我们通常对合并的那一维使用 sort，这个在 DP 优化部分会很常见。

例题

P3374 【模板】树状数组 1

动态一维数点。

我们将查询拆成两个前缀 \(r,l-1\) 作差的形式。

这样，修改 \((tim_i,x_i,v_i)\) 能对查询 \((tim_j,x_j)\) 产生贡献，除了上面的条件以外，仅需再满足 \(x_i\le x_j\)。

考虑到输入给定的序列已经天然地按 \(tim\) 不降了，所以不妨对 \(tim\) 分治，按 \(x\) 合并。

时间复杂度 \(O((n+m)\log(n+m))\)。

一个小优化，初始序列没有必要拆成 \(n\) 次修改操作，只需要在初始序列为 \(0\) 的答案上，额外累加 \(a_{l,r}\) 的总和即可。时间复杂度优化到 \(O(n+m\log m)\)。
点击查看代码 - R231360817

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=5e5+10;
struct Node{int id,x,k,c;}q[2*M],t[2*M];//id为询问编号，修改则是0
int n,m,a[N],idx,ans[M],qidx;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,s=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].x<=q[j].x;) s+=q[i].k,t[k++]=q[i++];
		ans[q[j].id]+=q[j].c*s;
		t[k++]=q[j++];
	}
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],a[i]+=a[i-1];
	for(int i=1,op,x,y;i<=m;i++){
		cin>>op>>x>>y;
		if(op==1){
			q[++idx]={0,x,y,0};
		}else{
			++qidx;
			q[++idx]={qidx,y,0,1};
			q[++idx]={qidx,x-1,0,-1};
			ans[qidx]=a[y]-a[x-1];
		}
	}
	cdq(1,idx);
	for(int i=1;i<=qidx;i++) cout<<ans[i]<<"\n";
	return 0;
}

P4390 [BalkanOI 2007] Mokia 摩基亚

动态二维数点。

时间复杂度 \(O((n+m)\log(n+m)\log n)\)。
点击查看代码 - R231361299

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5,Q=1.8e5+5;
struct Node{int id,x,y,yr,c,k;}a[Q];//(tim,x,y)
int n,idx,ans[Q],qidx,p[Q],t[Q];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
	inline int qry(int x,int y){return qry(y)-qry(x-1);}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[p[i]].x<=a[p[j]].x;i++){
			if(a[p[i]].k) bit.chp(a[p[i]].y,a[p[i]].k);
			t[k++]=p[i];
		}
		if(a[p[j]].c) ans[a[p[j]].id]+=a[p[j]].c*bit.qry(a[p[j]].y,a[p[j]].yr);
		t[k++]=p[j];
	}
	for(j=l;j<i;j++) if(a[p[j]].k) bit.clr(a[p[j]].y);
	while(i<=mid) t[k++]=p[i++];
	for(i=l;i<=r;i++) p[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>n;
	int op,x,y,xx,yy;
	while(cin>>op){
		if(op==1){
			cin>>x>>y>>xx;
			a[++idx]={0,x,y,0,0,xx};
		}else if(op==2){
			++qidx;
			cin>>x>>y>>xx>>yy;
			a[++idx]={qidx,xx,y,yy,1,0};
			a[++idx]={qidx,x-1,y,yy,-1,0};
		}else break;
	}
	for(int i=1;i<=idx;i++) p[i]=i;
	cdq(1,idx);
	for(int i=1;i<=qidx;i++) cout<<ans[i]<<"\n";
	return 0;
}

P3157 [CQOI2011] 动态逆序对

先求出初始状态的逆序对，再考虑删除操作带来的贡献。

令 \(tim_i\) 为 \(a_i\) 被删除的时间点，若未被删除则记为 \(m+1\)。

删除第 \(i\) 个元素，答案将会减少满足下面条件的 \(j\) 的个数：

• \(tim_j>tim_i\)
• \(x_j<x_i,v_j>v_i\) 或 \(x_j>x_i,v_j<v_i\)

由于 \(x,v\) 有两种关系需要讨论，所以 CDQ 过程中正反各遍历一次。

时间复杂度 \(O(m+n\log n)\)。
点击查看代码 - R229862409

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=5e4+10;
struct Node{int tim,x,v;}q[N],t[N];
inline bool cmp(Node& a,Node& b){return a.tim>b.tim;}
int n,m,cur,a[N],p[N],ans[M];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,c=0;
	cdq(l,mid),cdq(mid+1,r);
	for(i=mid,j=r;j>mid;j--){
		for(;i>=l&&q[i].x>q[j].x;i--) bit.chp(q[i].v,1);
		ans[q[j].tim]+=bit.qry(q[j].v);
	}
	for(j=mid;j>i;j--) bit.clr(q[j].v);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&q[i].x<q[j].x;i++){
			bit.chp(q[i].v,1),c++;
			t[k++]=q[i];
		}
		ans[q[j].tim]+=c-bit.qry(q[j].v);
		t[k++]=q[j];
	}
	for(j=l;j<i;j++) bit.clr(q[j].v);
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],p[a[i]]=i,q[i]={m+1,i,a[i]};
	for(int i=n;i;i--) cur+=bit.qry(a[i]-1),bit.chp(a[i],1);
	for(int i=1;i<=n;i++) bit.clr(a[i]);
	for(int i=1,x;i<=m;i++) cin>>x,q[p[x]].tim=i;
	sort(q+1,q+1+n,cmp),cdq(1,n);
	for(int i=1;i<=m;i++) cout<<cur<<"\n",cur-=ans[i];
	return 0;
}

P12685 [国家集训队] 排队 加强版

转化一下，这道题就是一个动态的二维数点问题。

我们将每个元素视作二维平面上的点 \((i,a_i)\)。

每次交换 \(l,r\) 两个元素时（\(l<r\)），都同时发生了修改操作和查询操作。

修改操作，就是将 \((l,a_l),(r,a_r)\) 处 \(-1\)，\((l,a_r),(r,a_l)\) 处 \(+1\)。

查询操作，即对答案的贡献为：

• 加上满足 \(j\in (l,r)\) 且 \(a_j<a_r\) 的 \(j\) 的个数。
• 减去满足 \(j\in (l,r)\) 且 \(a_j>a_r\) 的 \(j\) 的个数。
• 加上满足 \(j\in (l,r)\) 且 \(a_j>a_l\) 的 \(j\) 的个数。
• 减去满足 \(j\in (l,r)\) 且 \(a_j<a_l\) 的 \(j\) 的个数。
• 交换前若 \(a_l<a_r\) 则产生 \(1\) 的贡献，若 \(a_l>a_r\) 则产生 \(-1\) 的贡献。

再差分一下，每次交换带来的贡献可以写成 \(10\) 个前缀查询加减的形式，具体见代码。

每次交换，修改查询相互独立，两者顺序无所谓。

时间复杂度 \(O((n+m)\log (n+m)\log n)\)。
点击查看代码 - R229135369

#include<bits/stdc++.h>
#define int long long
#define eb emplace_back
using namespace std;
const int N=2e5+10,M=2e5+10;
int n,m,a[N],b[N],tn,idx,cur,ans[M];
struct Qr{bool op;int x,ix,c,id;}q[N+16*M],t[N+16*M];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=tn;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=tn;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].x<=q[j].x;){
			if(!q[i].op) bit.chp(q[i].ix,q[i].c);
			t[k++]=q[i++];
		}
		if(q[j].op) ans[q[j].id]+=q[j].c*bit.qry(q[j].ix);
		t[k++]=q[j++];
	}
	for(j=l;j<i;j++) if(!q[j].op) bit.clr(q[j].ix);
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
	sort(b+1,b+1+n),tn=unique(b+1,b+1+n)-b-1;
	for(int i=n;i;i--){
		a[i]=lower_bound(b+1,b+1+tn,a[i])-b;
		cur+=bit.qry(a[i]-1),q[++idx]={0,i,a[i],1,0};
		bit.chp(a[i],1);
	}
	for(int i=n;i;i--) bit.clr(a[i]);
	cin>>m;
	int l,r;
	for(int i=1;i<=m;i++){
		cin>>l>>r;
		if(a[l]==a[r]) continue;
		if(l>r) swap(l,r);
		q[++idx]={0,l,a[l],-1,i},q[++idx]={0,r,a[r],-1,i};
		q[++idx]={0,l,a[r],1,i},q[++idx]={0,r,a[l],1,i};
		if(l+1<r){
			if(a[r])
				q[++idx]={1,r-1,a[r]-1,1,i},q[++idx]={1,l,a[r]-1,-1,i};
			if(a[r]<tn)
				q[++idx]={1,r-1,tn,-1,i},q[++idx]={1,l,tn,1,i},
				q[++idx]={1,r-1,a[r],1,i},q[++idx]={1,l,a[r],-1,i};
			if(a[l])
				q[++idx]={1,r-1,a[l]-1,-1,i},q[++idx]={1,l,a[l]-1,1,i};
			if(a[l]<tn)
				q[++idx]={1,r-1,tn,1,i},q[++idx]={1,l,tn,-1,i},
				q[++idx]={1,r-1,a[l],-1,i},q[++idx]={1,l,a[l],1,i};
		}
		ans[i]=(a[l]<a[r]?1:-1),swap(a[l],a[r]);
	}
	cdq(1,idx);
	cout<<cur<<"\n";
	for(int i=1;i<=m;i++) cout<<(cur+=ans[i])<<"\n";
	return 0;
}

树状数组维护的那一维，可以不拆成前缀，因为树状数组上本身就可以查询一个区间的信息。

这样拆分数量就从 \(10\) 个降到了 \(8\) 个，分治的元素总数减少了，不过相应地结构体要额外加一个属性，存储树状数组上查询的另一个端点，这可能会增加一些转移负担。不过实测起来，效率的确有所提升（24.96s \(\rightarrow\) 21.80s）。
点击查看代码 - R229890062

#include<bits/stdc++.h>
#define int long long
#define eb emplace_back
using namespace std;
const int N=2e5+10,M=2e5+10;
int n,m,a[N],b[N],tn,idx,cur,ans[M];
struct Qr{bool op;int x,ix,iy,c,id;}q[N+12*M],t[N+12*M];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=tn;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<=tn;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].x<=q[j].x;){
			if(!q[i].op) bit.chp(q[i].ix,q[i].c);
			t[k++]=q[i++];
		}
		if(q[j].op) ans[q[j].id]+=q[j].c*(bit.qry(q[j].iy)-bit.qry(q[j].ix-1));
		t[k++]=q[j++];
	}
	for(j=l;j<i;j++) if(!q[j].op) bit.clr(q[j].ix);
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
	sort(b+1,b+1+n),tn=unique(b+1,b+1+n)-b-1;
	for(int i=n;i;i--){
		a[i]=lower_bound(b+1,b+1+tn,a[i])-b;
		cur+=bit.qry(a[i]-1),q[++idx]={0,i,a[i],0,1,0};
		bit.chp(a[i],1);
	}
	for(int i=n;i;i--) bit.clr(a[i]);
	cin>>m;
	int l,r;
	for(int i=1;i<=m;i++){
		cin>>l>>r;
		if(a[l]==a[r]) continue;
		if(l>r) swap(l,r);
		q[++idx]={0,l,a[l],0,-1,i},q[++idx]={0,r,a[r],0,-1,i};
		q[++idx]={0,l,a[r],0,1,i},q[++idx]={0,r,a[l],0,1,i};
		if(l+1<r){
			if(a[r])
				q[++idx]={1, r-1, 1,      a[r]-1, 1,  i},
				q[++idx]={1, l,   1,      a[r]-1, -1, i};
			if(a[r]<tn)
				q[++idx]={1, r-1, a[r]+1, tn,     -1, i},
				q[++idx]={1, l,   a[r]+1, tn,     1,  i};
			if(a[l]<tn)
				q[++idx]={1, r-1, a[l]+1, tn,     1,  i},
				q[++idx]={1, l,   a[l]+1, tn,     -1, i};
			if(a[l])
				q[++idx]={1, r-1, 1,      a[l]-1, -1, i},
				q[++idx]={1, l,   1,      a[l]-1, 1,  i};
		}
		ans[i]=(a[l]<a[r]?1:-1),swap(a[l],a[r]);
	}
	cdq(1,idx);
	cout<<cur<<"\n";
	for(int i=1;i<=m;i++) cout<<(cur+=ans[i])<<"\n";
	return 0;
}

P4169 [Violet] 天使玩偶 / SJY 摆棋子

先考虑只统计 \((x_i,y_i)\) 左下角的点应该如何做。

对于 \((x_j,y_j)\) 这个点，由于 \(x_j\le x_i,y_j\le y_i\)，所以绝对值可以拆开：

\[(x_i+y_i)-(x_j+y_j) \]

为了让其最小，我们要维护 \((x_j+y_j)\) 的 \(\max\) 值。

为了考虑所有的方向，我们用同样的方式跑 \(4\) 次 CDQ 分治，每跑完一次就将坐标系旋转 \(90^\circ\)。

时间复杂度 \(O((n+m)\log (n+m)\log V)\)。
点击查看代码 - R230522698

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10,M=3e5+10,Ve=1e6,V=Ve+10;
struct Node{int d1,d2,d3;bool op;}a[N+M],t[N+M];
bool cmpd1(Node a,Node b){return a.d1<b.d1;}
int n,m,idx,ans[M];
inline int lb(int x){return x&-x;}
void rot(){for(int i=1;i<=idx;i++) swap(a[i].d2,a[i].d3),a[i].d2=Ve-a[i].d2;}
struct BIT{
	int s[V];
	void chp(int x,int v){for(++x;x<V;x+=lb(x)) s[x]=max(s[x],v);}
	void clr(int x){for(++x;x<V;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	int qry(int x){int a=0;for(++x;x;x-=lb(x)) a=max(a,s[x]);return a?a:-3e6;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		while(i<=mid&&a[i].d2<=a[j].d2){
			if(!a[i].op) bit.chp(a[i].d3,a[i].d2+a[i].d3);
			t[k++]=a[i++];
		}
		if(a[j].op) ans[a[j].d1]=min(ans[a[j].d1],a[j].d2+a[j].d3-bit.qry(a[j].d3)); 
		t[k++]=a[j++];
	}
	for(j=l;j<i;j++) if(!a[j].op) bit.clr(a[j].d3);
	while(i<=mid) t[k++]=a[i++];
	for(i=l;i<=r;i++) a[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m,idx=n;
	memset(ans,0x3f,sizeof ans);
	for(int i=1;i<=n;i++) cin>>a[i].d2>>a[i].d3;
	for(int i=1,op,x,y;i<=m;i++) cin>>op>>x>>y,a[++idx]={i,x,y,op-1};
	for(int i=0;i<4;i++){
		if(i) rot(),sort(a+1,a+idx+1,cmpd1);
		cdq(1,idx);
	}
	for(int i=1;i<=m;i++) if(ans[i]!=ans[0]) cout<<ans[i]<<"\n";
	return 0;
}

P10633 BZOJ2989 数列 / BZOJ4170 极光

我们将每个元素视作二维平面上的点 \((i,a_i)\)。

查询操作就是求到某个点曼哈顿距离 \(\le k\) 的点的个数。

限制条件写成两个绝对值相加的形式实在不好做。

但是我们发现，到某个点的曼哈顿距离为定值 \(k\) 的点集，画出来是一个斜 \(45^\circ\) 的正方形。

也就是说，如果我们将坐标轴旋转 \(45^\circ\) 并放大 \(\sqrt{2}\) 倍，将每个点 \((x,y)\) 映射到 \((x+y,-x-y)\)，那么查询的区间就变成了一个以 \((x,y)\) 为中心，边长为 \(2k\) 的正方形，且它与 \(x,y\) 轴平行。

这其实就是曼哈顿距离和切比雪夫距离之间的转化，我们刚才从数形结合的角度理解了这一过程。OI Wiki 上有更为严谨的证明。
点击查看代码 - R231365554

#include<bits/stdc++.h>
using namespace std;
const int N=6e4+10,M=1.1e5,Ve=1e5,V=Ve+N;
struct Node{int id,x,il,ir,c;}q[4*M+N],t[4*M+N];
int n,m,idx,a[N],ans[M],qidx;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[V];
	inline void chp(int x,int v){for(;x<V;x+=lb(x)) s[x]+=v;}
	inline void clr(int x){for(;x<V;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	inline int qry(int x){int a=0;for(x=min(x,V-1),x=max(x,0);x;x-=lb(x)) a+=s[x];return a;}
	inline int qry(int x,int y){return qry(y)-qry(x-1);}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].x<=q[j].x;){
			if(!q[i].c) bit.chp(q[i].il,1);
			t[k++]=q[i++];
		}
		if(q[j].c) ans[q[j].id]+=q[j].c*bit.qry(q[j].il,q[j].ir);
		t[k++]=q[j++];
	}
	for(j=l;j<i;j++) if(!q[j].c) bit.clr(q[j].il);
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	cin>>n>>m,idx=n;
	for(int i=1;i<=n;i++) cin>>a[i],q[i]={0,a[i]+i,a[i]-i+n,0,0};
	string op;int x,k;
	for(int i=1;i<=m;i++){
		cin>>op>>x>>k;
		if(op[0]=='M'){
			a[x]=k;
			q[++idx]={0,k+x,k-x+n,0,0};//由于可能出现负数，所有y坐标都进行了+n处理
		}else{
			qidx++;
			q[++idx]={qidx,a[x]+x+k,a[x]-x-k+n,a[x]-x+k+n,1};
			q[++idx]={qidx,a[x]+x-k-1,a[x]-x-k+n,a[x]-x+k+n,-1};
		}
	}
	cdq(1,idx);
	for(int i=1;i<=qidx;i++) cout<<ans[i]<<"\n";
	return 0;
}

CF848C Goodbye Souvenir

"每种颜色最右边 \(−\) 最左边求和" 看起来不好直接维护，但是可以转化为"相邻同色位置的下标差求和"。

也就是说，如果令 \(pre_i\) 表示 \(a_i\) 上一次出现的位置（不存在则为 \(0\)），那么 \([l,r]\) 的答案就是：

\[\sum\limits_{i\le r,pre_i\ge l} i-pre_i \]

将 \((i,pre_i)\) 看作二维平面上的点，就是二维数点了。

不过还有一点，单点修改时，可能受影响的 \(pre\) 值有哪些？

• 被修改的位置。
• 与旧颜色相同的后一位。
• 与新颜色相同的后一位。

我们可以用 set 很方便地维护这些位置信息。
点击查看代码 - #334206726

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,M=1e5+10,V=1e5+10;
int n,m,a[N],idx,qidx;ll ans[M];
set<int> p[V];
struct Node{int id,p,pre,k;}q[N+6*M],t[N+6*M];
inline int lb(int x){return x&-x;}
struct BIT{//后缀BIT，值域[0,n)
	ll s[N];
	void chp(int x,int v){for(;x;x-=lb(x)) s[x]+=v;}
	void clr(int x){for(;x;x-=lb(x)) if(s[x]) s[x]=0;else return;}
	int qry(int x){int a=0;for(;x<n;x+=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].p<=q[j].p;){
			if(!q[i].id) bit.chp(q[i].pre,q[i].k);
			t[k++]=q[i++];
		}
		if(q[j].id) ans[q[j].id]+=bit.qry(q[j].pre);//查询>=q[j].pre
		t[k++]=q[j++];
	}
	for(j=l;j<i;j++) bit.clr(q[j].pre);
	while(i<=mid) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1,pre;i<=n;i++){
		cin>>a[i];
		pre=p[a[i]].empty()?0:(*p[a[i]].rbegin());
		q[++idx]={0,i,pre,i-pre};
		p[a[i]].insert(i);
	}
	int op,x,y,pre,nxt;
	set<int>::iterator it;
	for(int i=1;i<=m;i++){
		cin>>op>>x>>y;
		if(op==1){
			if(a[x]==y) continue;
			p[a[x]].erase(x);
			it=p[y].lower_bound(x+1),pre=0;//1.与新颜色相同的后一位
			if(it!=p[y].begin()) pre=*(--it);
			it=p[y].upper_bound(x);
			if(it!=p[y].end()){
				nxt=*it;
				q[++idx]={0,nxt,x,nxt-x};
				q[++idx]={0,nxt,pre,pre-nxt};
			}
			it=p[a[x]].lower_bound(x+1),pre=0;//2.与旧颜色相同的后一位
			if(it!=p[a[x]].begin()) pre=*(--it);
			it=p[a[x]].upper_bound(x);
			if(it!=p[a[x]].end()){
				nxt=*it;
				q[++idx]={0,nxt,pre,nxt-pre};
				q[++idx]={0,nxt,x,x-nxt};
			}
			q[++idx]={0,x,pre,pre-x};//3.被修改的位置
			a[x]=y,pre=0;
			it=p[y].lower_bound(x+1);
			if(it!=p[y].begin()) pre=*(--it);
			p[y].insert(x);
			q[++idx]={0,x,pre,x-pre};
		}else{
			q[++idx]={++qidx,y,x,0};//第一维∈[1,y]，第二维∈[x,n]
		}
	}
	cdq(1,idx);
	for(int i=1;i<=qidx;i++) cout<<ans[i]<<"\n";
	return 0;
}

P1903 [国家集训队] 数颜色 / 维护队列

本质上是 P1972 [SDOI2009] HH 的项链加了个点修。

我们沿用其思路来做。考虑单点修改时，可能受影响的 \(pre\) 值有哪些？

• 被修改的位置。
• 与旧颜色相同的后一位。
• 与新颜色相同的后一位。

我们可以用 set 很方便地维护这些位置信息。
点击查看代码 - R231365969

#include<bits/stdc++.h>
using namespace std;
const int N=133333+10,M=133333+10;
int n,m,tn,a[N],b[N+M],idx,qidx,ans[M];
unordered_map<int,int> ma;
set<int> p[N+M];
struct Query{char op;int x,y;}tq[M];
struct Node{int id,x,y,c;}q[N+6*M],t[N+6*M];
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else return;}
	int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		for(;i<=mid&&q[i].y<=q[j].y;){
			if(!q[i].id) bit.chp(q[i].x,q[i].c);
			t[k++]=q[i++];
		}
		if(q[j].id) ans[q[j].id]+=q[j].c*bit.qry(q[j].x);
		t[k++]=q[j++];
	}
	for(j=l;j<i;j++) bit.clr(q[j].x);
	for(;i<=mid;) t[k++]=q[i++];
	for(i=l;i<=r;i++) q[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],b[++tn]=a[i];
	for(int i=1;i<=m;i++){
		cin>>tq[i].op>>tq[i].x>>tq[i].y;
		if(tq[i].op=='R') b[++tn]=tq[i].y;
	}
	sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
	for(int i=1;i<=tn;i++) ma[b[i]]=i;
	for(int i=1,pre;i<=n;i++){
		a[i]=ma[a[i]];
		pre=p[a[i]].empty()?0:(*p[a[i]].rbegin());
		q[++idx]={0,i,pre,1};
		p[a[i]].insert(i);
	}
	set<int>::iterator it;
	for(int i=1,pre,nxt;i<=m;i++){
		auto [op,x,y]=tq[i];//仅c++17及以上可用，请勿在NOIp等考场上使用！
		if(op=='Q'){
			qidx++;
			q[++idx]={qidx,y,x-1,1};
			q[++idx]={qidx,x-1,x-1,-1};
		}else{
			y=ma[y];
			p[a[x]].erase(x);
			it=p[y].lower_bound(x+1),pre=0;//1.与新颜色相同的后一位
			if(it!=p[y].begin()) pre=*(--it);
			it=p[y].upper_bound(x);
			if(it!=p[y].end()){
				nxt=*it;
				q[++idx]={0,nxt,x,1};
				q[++idx]={0,nxt,pre,-1};
			}
			it=p[a[x]].lower_bound(x+1),pre=0;//2.与旧颜色相同的后一位
			if(it!=p[a[x]].begin()) pre=*(--it);
			it=p[a[x]].upper_bound(x);
			if(it!=p[a[x]].end()){
				nxt=*it;
				q[++idx]={0,nxt,x,-1};
				q[++idx]={0,nxt,pre,1};
			}
			q[++idx]={0,x,pre,-1};//3.被修改的位置
			a[x]=y,pre=0;
			it=p[y].lower_bound(x+1);
			if(it!=p[y].begin()) pre=*(--it);
			p[y].insert(x);
			q[++idx]={0,x,pre,1};
		}
	}
	cdq(1,idx);
	for(int i=1;i<=qidx;i++) cout<<ans[i]<<"\n";
	return 0;
}

P4690 [Ynoi Easy Round 2016] 镜中的昆虫

本质上是将上题的点修变成区修。

继续沿用上题的思路，就 \(pre\) 数组进行分析。查询和上题相同，我们主要分析区间赋值。

先给结论：对长度为 \(n\) 的序列进行 \(m\) 次区间赋值操作后，\(pre\) 数组的变化次数为 \(O(n+m)\) 级别。

简单证明一下：

如果我们将同色连续段称作一个块 ，那么不难发现，除了块的开头，其他位置的 \(pre\) 值全部都是其下标 \(-1\)。

而每次区修一定可以拆成若干个块拼起来（若不能恰好取到左右端点，则将左右端点所在的块分裂），修改完成后这些小的块会被消掉，变成一个大的块。则此过程中发生变化的 \(pre\) 值仅有：

• 这些块开头的 \(pre\) 值。
• 所操作的区间右侧，与各个块原颜色相同的第一个位置。

两者同阶，故每次操作 \(pre\) 的变化次数是 \(O(\text{删去的块的个数})\)，而每次我们最多添加 \(3\) 个块（左右端点所在的块分裂算 \(2\) 个，最后的大块算 \(1\) 个），所以删去的块的个数是 \(O(n+m)\) 数量级的，这样就得证了。

---

我们可以用 set 来维护每个块，对 \(pre\) 值的操作直接 CDQ 处理。

时间复杂度 \(O((n+m)\log^2 (n+m))\)。
点击查看代码 - R227633778

#include<bits/stdc++.h>
#include<ext/pb_ds/hash_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
using namespace std;
using namespace __gnu_pbds;
const int N=1e5+1,M=1e5+1;
int n,m,tn,a[N],b[N+M],pre[N],lst[N+M],st[N+M],top,idx,ans[M];
bitset<N+M> in;
struct Que{int l,r,x;}q[M];
gp_hash_table<int,int> ma;
set<int> ra,p[N+M];//ra记录所有块的左端点，p[i]记录颜色为i的所有块的左端点
struct Node{int d1,d2,d3,c,k;}c[10*N],t[10*N];//(d1,d2,d3,c,k)=(tim,i,pre_i,统计时的权重(±1),点修的参数)
bool cmp(Node a,Node b){return a.d1==b.d1?(a.d3==b.d3?a.d2<b.d2:a.d3<b.d3):a.d1<b.d1;}
void solve(int tim,int l,int r,int x){//将[l,r]置为x
	auto lp=--ra.lower_bound(l+1),rp=ra.upper_bound(r),tmp=lp;//左闭右开
	if(*lp!=l) p[a[*lp]].insert(l),pre[l]=l-1,a[l]=a[*lp],lp=ra.insert(l).first;//分裂左端点所在区间
	if(*rp!=r+1) p[a[*prev(rp)]].insert(r+1),pre[r+1]=r,a[r+1]=a[*prev(rp)],rp=ra.insert(r+1).first;//右端点
	in[st[++top]=x]=1;//st记录修改区间右侧需要更新的颜色
	for(bool f=1;lp!=rp;ra.erase(lp++)){//lp=ra.erase(lp)也可以
		p[a[*lp]].erase(*lp);
		c[++idx]={tim,*lp,pre[*lp],0,-1};
		if(f) f=0,c[++idx]={tim,*lp,pre[*lp]=((tmp=p[x].lower_bound(*lp))==p[x].begin()?0:*(ra.upper_bound(*(--tmp)))-1),0,1};
		else c[++idx]={tim,*lp,pre[*lp]=*lp-1,0,1};//最左边的段需要查找前面的同色位置，其他段修改为i-1即可
		if(!in[a[*lp]]) in[st[++top]=a[*lp]]=1;
		a[*lp]=x;//由于每次访问都是在块的开头，所以更新也只操作块的开头元素即可
	}
	ra.insert(l),p[x].insert(l);
	int z;
	while(top){//处理修改区间右侧的pre
		in[z=st[top--]]=0;
		auto nxt=p[z].upper_bound(r);
		if(nxt!=p[z].end()){
			c[++idx]={tim,*nxt,pre[*nxt],0,-1};
			c[++idx]={tim,*nxt,pre[*nxt]=((tmp=p[z].lower_bound(*nxt))==p[z].begin()?0:*(ra.upper_bound(*(--tmp)))-1),0,1};
		}
	}
}
inline int lb(int x){return x&-x;}
struct BIT{
	int s[N];
	void chp(int x,int v){for(;x<=n;x+=lb(x)) s[x]+=v;}
	void clr(int x){for(;x<=n;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid),cdq(mid+1,r);
	for(i=k=l,j=mid+1;j<=r;){
		while(i<=mid&&c[i].d3<=c[j].d3){
			if(c[i].k) bit.chp(c[i].d2,c[i].k);
			t[k++]=c[i++];
		}
		if(!c[j].k) ans[c[j].d1]+=c[j].c*bit.qry(c[j].d2);
		t[k++]=c[j++];
	}
	for(j=l;j<i;j++) if(c[j].k) bit.clr(c[j].d2);
	while(i<=mid) t[k++]=c[i++];
	for(i=l;i<=r;i++) c[i]=t[i];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m,tn=n;
	for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
	for(int i=1,o;i<=m;i++){
		cin>>o>>q[i].l>>q[i].r;
		if(2-o) cin>>q[i].x,b[++tn]=q[i].x;
	}
	sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
	for(int i=1;i<=tn;i++) ma[b[i]]=i;
	for(int i=1;i<=n;i++){
		a[i]=ma[a[i]];
		c[++idx]={0,i,pre[i]=lst[a[i]],0,1},lst[a[i]]=i;
		if(a[i]!=a[i-1]) ra.insert(i),p[a[i]].insert(i);
	}
	ra.insert(0),ra.insert(n+1);
	for(int i=1;i<=m;i++){
		auto [l,r,x]=q[i];
		if(l>r) continue;
		if(x) solve(i,l,r,ma[x]);
		else c[++idx]={i,r,l-1,1,0},c[++idx]={i,l-1,l-1,-1,0};
	}
	cdq(1,idx);
	for(int i=1;i<=m;i++) if(ans[i]) cout<<ans[i]<<"\n";
	return 0;
}

惊了，居然拿了洛谷最优解_{（现在不是了）}？我也妹卡常啊 ( o o

总之 solve() 是真的难写难调啊。

在 LOJ 上看到了实现出人意料简洁的代码，见 #1748229。实现方法也是 CDQ 分治，如果有兴趣可以去学习一下。

优化 1D / 1D 动态规划的转移

1D / 1D 动态规划 指的是一类特定的 DP 问题，该类题目的特征是 DP 数组是一维的，转移是 \(O(n)\) 的。如果条件良好的话，有时可以通过 CDQ 分治来把它们的时间复杂度由 \(O(n^2)\) 降至 \(O(n\log^2n)\)。
------ OI Wiki

举个例子，对于长度为 \(n\) 的序列，每个元素有属性 \(a,b\)。

\(f_i=1+\max_j f_j\)，其中 \(j\) 满足 \(a_j<a_i,b_j<b_i\)（\(a\) 互不相同）。

本质上还是点对间的互相贡献，因此考虑使用 CDQ 分治。

贡献的记入和统计和之前是相同的，不再赘述。

不过需要注意，这里的转移是有严格的顺序要求的，一个位置要想参与转移，其本身的 DP 值必须已经被计算好。

这和动转静问题中处理"有时序依赖关系" 操作时遇到的问题是一样的。

所以我们仍需要采取中序遍历的方法，先 cdq(l,mid)，再跨区间转移，最后 cdq(mid+1,r)。

这样，在 cdq(l,r) 结束时，\(f_l,f_{l+1},\dots,f_r\) 应该都被计算完毕。

上部分也提到过，中序遍历会破坏分治排序的结构，这种情况下我们一般对合并的那一位使用 sort，毕竟为了防止"代码过于复杂" 导致的各种错误，舍弃一点效率也是可以的。

况且如果你使用数据结构维护了某一维，时间复杂度的瓶颈就不止是 sort 了，还有数据结构。所以就算不用 sort 也仅仅是减小了常数而已。

所以说下文中我们会用到大量的 sort，如果你有"cmp 函数为什么这样写" 之类的疑惑的话，请到文章末尾看看关于 cmp 函数的说明。结合前文的分析应该不难理解这样做的正确性。

例题

B3637 最长上升子序列

可以结合代码来理解。

令 \(f_i\) 为以 \(i\) 结尾的最长上升子序列长度，则有转移：

\[f_j=1+\max_i f_i \]

其中 \(i\) 满足：

• \(id_i<id_j\)
• \(x_i<x_j\)

我们对 \(id\) 分治，按 \(x\) 合并。

由于我们没有归并排序，所以时间复杂度是 \(O(n\log^2 n)\)。
点击查看代码 - R231707004

#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;
int n,f[N];
struct Node{int id,x;}a[N],t[N];
bool cmp_id(const Node& a,const Node& b){return a.id<b.id;}
bool cmp_x(const Node& a,const Node& b){return a.x<b.x;}
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,mx=0;
	cdq(l,mid);
	for(i=mid+1;i<=r;i++) t[i]=a[i];
	sort(a+l,a+mid+1,cmp_x),sort(a+mid+1,a+r+1,cmp_x);//对x排序
	for(i=l,j=mid+1;j<=r;j++){//按x合并
		while(i<=mid&&a[i].x<a[j].x) mx=max(mx,f[a[i++].id]);
		f[a[j].id]=max(f[a[j].id],mx+1);
	}
	for(i=mid+1;i<=r;i++) a[i]=t[i];//注意需要将右区间还原成id有序的状态
	cdq(mid+1,r);
}
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].x,a[i].id=i;
	f[1]=1;
	cdq(1,n);
	cout<<*max_element(f+1,f+1+n)<<"\n";
	return 0;
}return 0;
}

P4093 [HEOI2016 / TJOI2016] 序列

我们用 \(mn_i\) 表示 \(a_i\) 能够变到的最小值，\(mx_i\) 表示能变到的最大值，\(f_i\) 为以 \(i\) 结尾的最长子序列长度，则有转移：

\[f_j=1+\max_i f_i \]

其中 \(i\) 满足：

• \(id_i<id_j\)
• \(x_i\le mn_j\)
• \(mx_i\le x_j\)

我们可以对 \(id\) 分治，解决第一维。

左区间按 \(x\) 排序，右区间按 \(mn\) 排序，双指针解决第二维。

树状数组维护第三维。具体来说，记入贡献时将第 \(mx_i\) 位与 \(x_j\) 取 \(\max\)，统计贡献时查询 \(\le x_j\) 位置的 \(\max\)。

尽管 \(\max\) 不可差分，但我们查询的区间始终是一个前缀，所以可以用树状数组来维护。

时间复杂度 \(O(m+n\log^2 n)\)。
点击查看代码 - R231708020

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,V=1e5+10;
int n,m,f[N];
struct Node{int id,x,mx,mn;}a[N],t[N];
inline bool cmpid(Node& a,Node& b){return a.id<b.id;}
inline bool cmpx(Node& a,Node& b){return a.x<b.x;}
inline bool cmpmx(Node& a,Node& b){return a.mx<b.mx;}
inline int lb(int x){return x&-x;}
struct BIT{
	int mx[V];
	inline void chp(int x,int v){for(;x<V;x+=lb(x)) mx[x]=max(mx[x],v);}
	inline void clr(int x){for(;x<V;x+=lb(x)) if(mx[x]) mx[x]=0;else return;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a=max(a,mx[x]);return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j;
	cdq(l,mid);
	for(i=mid+1;i<=r;i++) t[i]=a[i];
	sort(a+l,a+mid+1,cmpmx),sort(a+mid+1,a+r+1,cmpx);
	for(i=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[i].mx<=a[j].x;i++) bit.chp(a[i].x,f[a[i].id]);
		f[a[j].id]=max(f[a[j].id],bit.qry(a[j].mn)+1);
	}
	for(j=l;j<i;j++) bit.clr(a[j].x);
	for(i=mid+1;i<=r;i++) a[i]=t[i];
	cdq(mid+1,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1,x;i<=n;i++) cin>>x,a[i]={i,x,x,x};
	for(int i=1,x,y;i<=m;i++){
		cin>>x>>y;
		a[x].mx=max(a[x].mx,y);
		a[x].mn=min(a[x].mn,y);
	}
	f[1]=1;
	cdq(1,n);
	cout<<*max_element(f+1,f+1+n)<<"\n";
	return 0;
}

P3364 Cool loves touli

用 \(a_i,b_i,c_i\) 分别表示每个英雄的 \(3\) 个属性，用 \(f_i\) 表示以 \(i\) 结尾的最长子序列长度，则有转移：

\[f_j=1+\max_i f_i \]

其中 \(i\) 满足：

• \(id_i<id_j\)
• \(c_i\le a_j\)
• \(b_i\le c_j\)

转移和上题完全一样。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R231708552

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
const int N=1e5+10;
gp_hash_table<int,int> ma;
struct Node{int d1,d2,d3,d4,id;}a[N],t[N];
bool cmpd1(Node a,Node b){return a.d1<b.d1;}
bool cmpd3(Node a,Node b){return a.d3<b.d3;}
bool cmpd4(Node a,Node b){return a.d4<b.d4;}
int n,w[N],f[N],b[3*N],tn;
inline int lb(int x){return x&-x;}
struct BIT{
	int s[3*N];
	void chp(int x,int v){for(;x<=tn;x+=lb(x)) s[x]=max(s[x],v);}
	void clr(int x){for(;x<=tn;x+=lb(x)) if(s[x]) s[x]=0;else break;}
	int qry(int x){int a=0;for(;x;x-=lb(x)) a=max(a,s[x]);return a;}
}bit;
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq(l,mid);
	for(i=mid+1;i<=r;i++) t[i]=a[i];
	sort(a+l,a+mid+1,cmpd3),sort(a+mid+1,a+r+1,cmpd4);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[i].d3<=a[j].d4;i++) bit.chp(a[i].d4,f[a[i].id]);
		f[a[j].id]=max(f[a[j].id],bit.qry(a[j].d2)+1);
	}
	for(j=l;j<i;j++) bit.clr(a[j].d4);
	for(i=mid+1;i<=r;i++) a[i]=t[i];
	cdq(mid+1,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].d1>>a[i].d2>>a[i].d3>>a[i].d4,a[i].id=i,b[++tn]=a[i].d2,b[++tn]=a[i].d3,b[++tn]=a[i].d4;
	sort(b+1,b+1+tn),tn=unique(b+1,b+1+tn)-b-1;
	for(int i=1;i<=tn;i++) ma[b[i]]=i;
	for(int i=1;i<=n;i++) a[i].d2=ma[a[i].d2],a[i].d3=ma[a[i].d3],a[i].d4=ma[a[i].d4],f[i]=1;
	sort(a+1,a+1+n,cmpd1),cdq(1,n);
	cout<<*max_element(f+1,f+1+n)<<"\n";
	return 0;
}

P5621 [DBOI2019] 德丽莎世界第一可爱

\(i\) 转移到 \(j\) 需要满足四个属性均 \(\le j\)。

仿照四维偏序来写，没什么可说的，注意两层 CDQ 都要按中序遍历进行。

时间复杂度 \(O(n\log^3 n)\)。
点击查看代码 - R231709287

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,V=2e5+2,O=1e5+1;
int n,s[N],f[N];
struct Node{int d1,d2,d3,d4,id;bool s;}a[N],t2d[N],t3d[N];
inline bool cmpd1(Node a,Node b){return a.d1==b.d1?(a.d2==b.d2?(a.d3==b.d3?(a.d4==b.d4?a.id<b.id:a.d4<b.d4):a.d3<b.d3):a.d2<b.d2):a.d1<b.d1;}
inline bool cmpd2(Node a,Node b){return a.d2==b.d2?(a.d3==b.d3?(a.d4==b.d4?(a.d1==b.d1?a.id<b.id:a.d1<b.d1):a.d4<b.d4):a.d3<b.d3):a.d2<b.d2;}
inline bool cmpd3(Node a,Node b){return a.d3<b.d3;}
inline int lb(int x){return x&-x;}
struct BIT{
	int s[V];
	inline void init(){memset(s,-0x3f,sizeof s);}
	inline void chp(int x,int v){for(x+=O;x<V;x+=lb(x)) s[x]=max(s[x],v);}
	inline void clr(int x){for(x+=O;x<V;x+=lb(x)) if(s[x]!=s[0]) s[x]=s[0];else return;}
	inline int qry(int x){int a=0;for(x+=O;x;x-=lb(x)) a=max(a,s[x]);return a;}
}bit;
void cdq3d(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k;
	cdq3d(l,mid);
	for(i=mid+1;i<=r;i++) t3d[i]=t2d[i];
	sort(t2d+l,t2d+mid+1,cmpd3),sort(t2d+mid+1,t2d+r+1,cmpd3);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&t2d[i].d3<=t2d[j].d3;i++) if(!t2d[i].s) bit.chp(t2d[i].d4,f[t2d[i].id]);
		if(t2d[j].s) f[t2d[j].id]=max(f[t2d[j].id],bit.qry(t2d[j].d4)+s[t2d[j].id]);
	}
	for(j=l;j<i;j++) if(!t2d[j].s) bit.clr(t2d[j].d4);
	for(i=mid+1;i<=r;i++) t2d[i]=t3d[i];
	cdq3d(mid+1,r);
}
void cdq2d(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i;
	cdq2d(l,mid);
	for(i=l;i<=mid;i++) a[i].s=0,t2d[i]=a[i];
	for(i=mid+1;i<=r;i++) a[i].s=1,t2d[i]=a[i];
	sort(t2d+l,t2d+r+1,cmpd2),cdq3d(l,r);
	cdq2d(mid+1,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	bit.init();
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].d1>>a[i].d2>>a[i].d3>>a[i].d4>>s[i],a[i].id=i;
	for(int i=1;i<=n;i++) f[i]=s[i];
	sort(a+1,a+1+n,cmpd1),cdq2d(1,n);
	cout<<*max_element(f+1,f+1+n);
	return 0;
}

P2487 [SDOI2011] 拦截导弹

这道题有两问，第一问是一个二维最长不降子序列，加上 \(tim\) 相当于三维偏序，直接 DP 就行。

第二问是每个元素被选入最长不降子序列的概率。

我们记 \(f_1[i],g_1[i]\) 分别为以 \(i\) 结尾的长度和方案数，\(f_2[i],g_2[i]\) 分别为以 \(i\) 开头的长度和方案数。

则一个元素有可能属于某个最长不降子序列，当且仅当 \(f_1[i]+f_2[i]-1=f_1[n]\)。

计算概率则为 \(\Large\frac{g_1[i]\times g_2[i]}{\sum g_1[i]}\)。

\(g\) 的计算，仅需在 \(f\) 转移的过程中判定：

• 如果 \(f_{i}+1=f_{j}\)，则 \(g_{j}\leftarrow g_{j}+g_{i}\)。
• 如果 \(f_{i}+1>f_{j}\)，则 \(g_{j}\leftarrow g_{i}\)。

代码实现要跑两次 CDQ，一个算结尾，一个算开头。

为了减少码量，我将"以 \(i\) 开头的最长不降子序列" 的答案转化为了"数组反转后，以 \(j\) 开头的最长不增子序列"。这样我们仅需写一个 CDQ，根据 CDQ 的轮次更改比较规则，并在第二次 CDQ 之前反转一下原数组即可。

时间复杂度 \(O(n\log^2 n)\)。
点击查看代码 - R231709847

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int n,f[2][N];
bool flg;
struct Node{int id,a,b;}a[N],t[N];
double sum,g[2][N];
inline int lb(int x){return x&-x;}
struct BIT{
	int mx[N];double c[N];
	void chp(int x,int _mx,double _c){for(;x<=n;x+=lb(x)) if(_mx==mx[x]) c[x]+=_c;else if(_mx>mx[x]) c[x]=_c,mx[x]=_mx;}
	void clr(int x){for(;x<=n;x+=lb(x)) if(mx[x]) mx[x]=c[x]=0;else break;}
	void qry(int x,int &_mx,double &_c){
		_mx=_c=0;
		for(;x;x-=lb(x)) if(mx[x]==_mx) _c+=c[x];else if(mx[x]>_mx) _c=c[x],_mx=mx[x];
	}
}bit;
inline bool cmpb(Node a,Node b){return flg?a.b<b.b:a.b>b.b;}
inline bool cmpa(Node a,Node b){
	return a.a==b.a?a.id<b.id:(flg?a.a<b.a:a.a>b.a);
}
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,mx;double c;
	cdq(l,mid);
	for(i=mid+1;i<=r;i++) t[i]=a[i];
	sort(a+l,a+mid+1,cmpb),sort(a+mid+1,a+r+1,cmpb);
	for(i=l,j=mid+1;j<=r;j++){
		while(i<=mid&&(a[i].b==a[j].b||cmpb(a[i],a[j]))) bit.chp(a[i].id,f[flg][a[i].id],g[flg][a[i].id]),i++;
		bit.qry(a[j].id-1,mx,c);
		if(mx+1==f[flg][a[j].id]) g[flg][a[j].id]+=c;
		else if(mx+1>f[flg][a[j].id]) f[flg][a[j].id]=mx+1,g[flg][a[j].id]=c;
	}
	for(i=l;i<=mid;i++) bit.clr(a[i].id);
	for(i=mid+1;i<=r;i++) a[i]=t[i];
	cdq(mid+1,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b,a[i].id=i,g[0][i]=g[1][i]=f[0][i]=f[1][i]=1;
	flg=0,sort(a+1,a+1+n,cmpa),cdq(1,n);
	for(int i=1;i<=n;i++) a[i].id=n-a[i].id+1;
	flg=1,sort(a+1,a+1+n,cmpa),cdq(1,n);//由于id反转，所以f[1],g[1]也是反着存的
	int mx=*max_element(f[0]+1,f[0]+n+1);
	for(int i=1;i<=n;i++) if(f[0][i]==mx) sum+=g[0][i];
	cout<<mx<<"\n";
	for(int i=1;i<=n;i++){
		if(f[0][i]+f[1][n-i+1]-1==mx) cout<<fixed<<setprecision(5)<<g[0][i]*g[1][n-i+1]/sum<<" ";
		else cout<<"0.00000 ";
	}
	return 0;
}

P6007 [USACO20JAN] Springboards G

令 \(f_i\) 为走到第 \(i\) 个跳板的终点，最多能省下多少路程。

则有转移：

\[f_j=w_j+\max_i f_i \]

其中 \(w_i\) 为跳板 \(i\) 能跨越的路程，即 \(x_2[i]-x_1[i]+y_2[i]-y_1[i]\)。

\(i\) 需要满足：

• \(x_2[i]\le x_1[j]\)
• \(y_2[i]\le y_1[j]\)

不过代码实现中，为了减少单个节点存储的属性个数，我把一个跳板拆成两个点了，这样转移时：

• \(x_i\le x_j\)
• \(y_i\le y_j\)
• \(i\) 是一个跳板的终点
• \(j\) 是一个跳板的起点

这样限制一下就可以了。

时间复杂度 \(O(n\log n)\)。
点击查看代码 - R231705070

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct Node{int x,y,id;bool t;}a[N<<1],t[N<<1];
inline bool cmpx(Node a,Node b){return a.x==b.x?(a.y==b.y?a.t>b.t:a.y<b.y):a.x<b.x;}
inline bool cmpy(Node a,Node b){return a.y<b.y;}// ↑ 注意位置相同时要将统计贡献放在记入贡献的后面
int k,n,idx,w[N],f[N];
void cdq(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1,i,j,k,mx=INT_MIN;
	cdq(l,mid);
	for(i=mid+1;i<=r;i++) t[i]=a[i];
	sort(a+l,a+mid+1,cmpy),sort(a+mid+1,a+r+1,cmpy);
	for(i=k=l,j=mid+1;j<=r;j++){
		for(;i<=mid&&a[i].y<=a[j].y;i++){
			if(a[i].t) mx=max(mx,f[a[i].id]);
		}
		if(!a[j].t) f[a[j].id]=max(f[a[j].id],mx+w[a[j].id]);
	}
	for(i=mid+1;i<=r;i++) a[i]=t[i];
	cdq(mid+1,r);
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>k>>n;
	for(int i=1,x,y,xx,yy;i<=n;i++){
		cin>>x>>y>>xx>>yy;
		a[++idx]={x,y,i,0};
		a[++idx]={xx,yy,i,1};
		w[i]=f[i]=xx+yy-x-y;
	}
	a[++idx]={k,k,0,0};
	sort(a+1,a+1+idx,cmpx),cdq(1,idx);
	cout<<2*k-f[0]<<"\n";
	return 0;
}

细节

小 Trick

随时更新。

• 卡常小技巧：拿三维偏序举例，CDQ 过程中每个区间都存在 \(O((r-l+1)^2)\) 的暴力，因此如果 \(r-l+1<\log n\) 的话可以直接暴力。
• 用于分治的那一维（比如时间戳）若已经自然有序，可以直接不存储这个属性。
• 可以将值域小的属性丢给树状数组，值域大的属性丢给排序 / 分治，这样有时可以省去离散化。
• Flash_Hu 的博客提到，我们可以不对每个元素封装 struct，而是用数组来存每个属性，仅记录每个元素的索引。这样排序时转移的也是若干整数，而非若干结构体变量。可以减少转移负担，不过相应的增加了数组的访问。或许只有属性较多的情况下才能体现出优势来，不过这个我也没有实测。
• UOJ 群里说 cdq 做动态问题，当下主流的写法是仅对修改操作分治，查询操作用 vector 挂在修改操作的后面。我没怎么写过，如果有兴趣可以参考 这份代码，效率并未实测。
• 云浅 的博客中给出了一种 \(O(n\log n)\) 计算三维偏序的算法。不过其有一定局限性，不能算出特定三元组产生的贡献，并且偏序条件必须包含 =。由于和 CDQ 关系不大，这里就不加说明了。

关于所有维度都严格小于的偏序问题

前文我们提到，在这种条件下，我们只能对没有重复值的那一维进行分治，否则不能保证"左区间的该属性 \(<\) 右区间的该属性"。

可如果恰好所有维度都有重复元素呢？

不知道你有没有见过这样的题，反正我是没见过，所以我造了几道。

二维偏序（严格小于） ~ 三维偏序（严格小于） ~ 四维偏序（严格小于）

经过 vuqa 和谷讨论区，我得到了一个可行的解决方法（from lzyqwq）。

就是将询问单独提出来，就是额外加 \(n\) 个点，每个查询形如"第一维 \(\le a_i-1\)，第二维 \(\le b_i-1\)，......"，就是数点问题了。

std 放在每个题面的下方了。

关于 cmp 函数

写 cmp 的宗旨就是：对于一个元素，把所有为它提供贡献的元素放在它的左边。

这个原理我们很容易理解，但是真正落实到代码上，我们可能会有很多困惑（尤其是我）。

这 cmp 到底该怎么写？

什么时候判等号，什么时候需要顾及更高维的属性，什么时候比较当前这一维就可以了？

简单来说：

• 用于分治的最内层的属性，排序是只考虑自己的值就可以了。

• 其他属性，排序时都需要额外考虑其他属性（作为第 \(2,3,\dots\) 关键字，顺序无所谓）。

  特别地，若某一属性无重复元素，则只需额外考虑这一个属性（相当于把不必要的等号去掉了）。

关于 sort 和 stable_sort

在前文我们提及了 stable_sort 的作用，在这里比较一下两个函数的使用。

如果你使用 sort：

• 需要预先处理完全相同的元素（如果有的话）：去重，或者添加一个互不相同的属性。
• cmp 函数要按上面第二条的规则来写。

如果你使用 stable_sort / 归并：

• 无需处理重复元素问题。

• cmp 函数仅需在主函数的排序中按上面的规则来写，其他属性只需要考虑自己这一维就行了。

  原因前文提到过：自定义规则下相等的元素，在 stable_sort 中会保持相对顺序不变。

后

本文较长，难免有疏漏和谬误~~（有超级奇怪的表述也说不定呢）~~。如果有疑问或者修正或者补充说明，请发在评论区，我会认真阅读的！

CDQ 套斜率优化什么的......如果有空会写（逃）
后话
从初识这个算法到完成这篇笔记（7/20~8/18），已经过去了将近一个月的时间。

这段时间内，我学习的途径完全来自网络。阅读各路大神的博客，与谷 u 讨论，在 UOJ 裙求助......

虽然信竞是一门十分依赖选手之间交流的竞赛，不过我发觉到网络上的知识是十分零散的（"细节" 部分的内容几乎没有博客单独提出来强调），要想真正解答疑惑，请教别人是必不可少的过程。除此之外还要对当下主流的算法达到熟练掌握（例如那个挂 vector 的写法）。我想这也印证了信息竞赛正在成为"圈子竞赛" 这个观点吧。

在求助于别人和自己的思考当中，我逐渐理清了算法的各种细节，也理清了我混乱的思路。

但同时，也深深感觉到，自己已经落下别人太远了。

不仅在算法、数据结构的掌握方面，更在于自己的思维、策略方面。

同校的信竞大神已经在初二初三就开始参加省选的集训了，同为初三（准高一）的我，相比之下完全不算有天赋、有实力的人，努力也绝对比不上他们，所以不能走得太远，打完今年的 NOIp 我应该就退役了（如果能够省一的话）；文化课方面处处爆杀我的也大有人在。因此我常常感到无可适从，不过总会到头的，毕竟信竞陪伴我的时间可能已经开始倒计时了。

有人和我说，一个注定了留不住的东西，你还要在上面做什么文章？专心弄文化课，或者至少在 NOIp 前把你提高级的知识点搞好就很厉害了。

不知道大家如何，反正我做一件事情，一旦在中途产生对"目的" 的疑惑，整个人就会变得空虚、迷茫。

开这个坑后的一段时间，这种感觉时不时缠绕着我，或许是出于退役前的倔强吧，这种时候越是需要冷静，我就越往前死磕，一天下来除了做了几道题之外，自己悟透了什么？好像没有。

不过在这篇博客完成过半时，我找到了自己开始写博客的初衷。

我写这些博客，不光是为了自己，更是为了像现在的我这样困惑的后人。不会有人永远困惑，但永远都会有人困惑。

想到了稗田阿求，为了"先代" 也好，为了"人类" 也好，总要有东西支持她义无反顾地完成这一切（无端联想）。

牛逼！又多活一天

还有一部分原因，应该就是为了给自己留下一点回忆吧。虽然现在还是心存不舍，不过这样一想，选择了这条路的自己和选择了那条路的自己，到底还是一个人嘛。

至少，我心念的旧物，曾带给了我过什么，或许是解题的思维，或许是 AC 的喜悦，或许是一路同行的伙伴。

我一定也在这方面为别人带来了什么，或许是知识，或许是答疑解惑，或许是将互相产生贡献的精神传承了一下。

心有这个念想足矣，在我重新起步的时候，我会坦然地说：

曾经拥有它真的太好了。

---

我会尽力的。希望大学还能回来！

引用致谢：

• OI Wiki - CDQ 分治
• mlystdcall - 【教程】CDQ 套 CDQ------ 四维偏序问题
• complete_binary_tree - 题解：P3810 【模板】三维偏序（陌上花开）
• Flash_Hu - CDQ 分治总结（CDQ，树状数组，归并排序）

\[\Large\underline{\text{CDQ Divide}}_{\text{ last update on 2025/8/18}}\\ \]

\[\small\text{～　冷　氣　開　放　注　意　～} \]