在之前的链表学习中,我们掌握了基本的增删改查和双指针技巧。今天,我们要挑战链表操作的"深水区"。
我们将通过两个非常有代表性的题目:K个一组翻转链表 和 链表排序 ,来探讨如何在复杂的指针变换中保持逻辑清晰,以及如何将分治算法完美应用到链表结构中。这两个问题不依赖额外的数据结构,完全依靠对 next 指针的掌控,是磨练代码基本功的绝佳素材。
一、 K个一组翻转链表 (Reverse Nodes in k-Group)
这个问题的难点不在于"翻转",而在于"分组"和"缝合"。我们需要将链表切分成若干个长度为 k 的小段,对每一段进行内部翻转,然后再把这些翻转后的小段按照原来的顺序重新连起来。
1. 核心思路:维护"守门员" p0
如果只是单纯翻转一个链表,我们只需要 pre、cur、nxt 三个指针就够了。但在 K 个一组的场景下,每一组翻转后,都需要跟上一组的尾巴 和下一组的头建立连接。
因此,我们需要一个关键指针 p0。
-
p0 的定义 :它始终指向当前待翻转这一组的前一个节点。
-
作用:它就像一个"守门员"或"锚点",负责在这一组翻转完毕后,把断开的链表重新缝合起来。
2. 代码解析
代码采用了先统计长度,再循环处理的逻辑。
C++代码实现:
cpp
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
// 1. 统计链表总长度
ListNode* cur = head;
int len = 0;
while (cur) {
len += 1;
cur = cur->next;
}
// 2. 初始化 dummy 节点和 p0
ListNode dummy(0, head);
ListNode* p0 = &dummy;
cur = head; // cur 复位,准备开始干活
ListNode* pre = nullptr;
// 3. 循环处理每一组,条件是剩余长度 >= k
while (len >= k) {
len -= k;
// --- 内部翻转逻辑 (标准的链表翻转) ---
for (int i = 0; i < k; ++i) {
ListNode* nxt = cur->next;
cur->next = pre;
pre = cur;
cur = nxt;
}
// --- 缝合逻辑 (最难理解的部分) ---
// 此时状态:
// p0 -> [原来的头...原来的尾] -> cur(下一组头)
// 翻转后:
// p0 依然指向 dummy/上一组尾
// pre 指向 [现在的头(原来的尾)]
// p0->next 指向 [现在的尾(原来的头)]
ListNode* nxt = p0->next; // nxt 暂存的是这一组"原来的头",现在它变成了尾巴
// 步骤 A: 将 p0 连接到 现在的头 (pre)
// 这一步修正了上一组和当前组的连接
p0->next->next = cur;
p0->next = pre;
// 步骤 B: 移动 p0
// p0 移动到这一组的尾巴 (也就是 nxt),为下一组做好准备
p0 = nxt;
}
return dummy.next;
}
};3. 难点拆解:缝合过程
代码中最晦涩的这四行:
C++代码实现:
cpp
ListNode* nxt = p0->next;
p0->next->next = cur;
p0->next = pre;
p0 = nxt;图解:
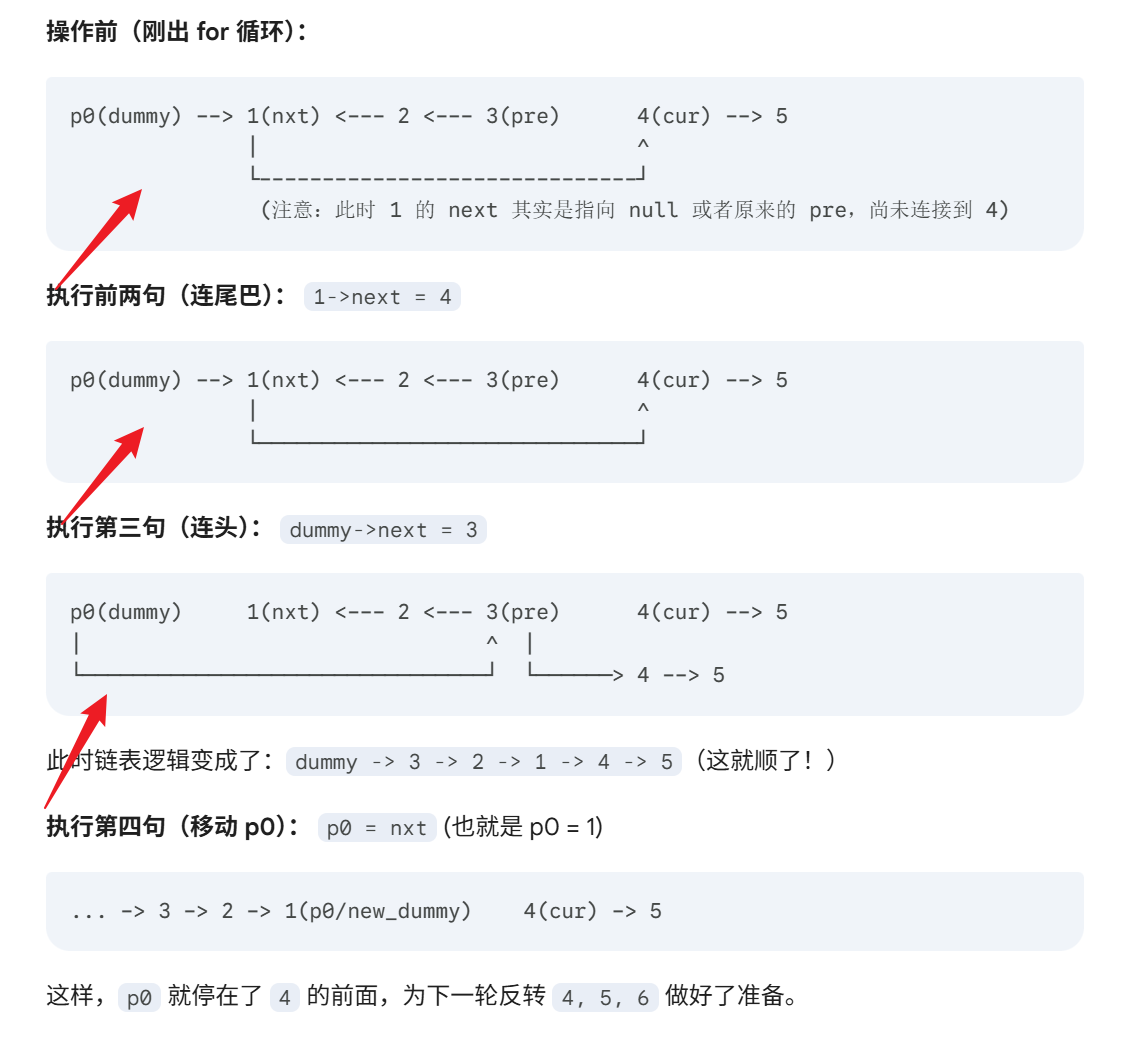
我们可以这样理解:
-
锁定旧头 :
nxt = p0->next。因为翻转前p0->next指向这一组的第一个元素(例如 1),翻转后它变成了这组的最后一个元素。 -
连接下组 :
p0->next->next = cur。也就是让 1 指向下一组的开头(例如 4)。等价于1->next = 4。 -
连接上组 :
p0->next = pre。让p0指向这一组翻转后的新头(例如 3)。等价于dummy->next = 3。 -
移动 p0 :
p0 = nxt。当前组处理完了,p0跳到 1 的位置,蹲守在 4 的前面,准备处理下一组。
4. 复杂度分析
-
时间复杂度:O(N)。我们需要先遍历一次求长度,然后再次遍历翻转。每个节点最多被访问两次,所以是线性的。
-
空间复杂度:O(1)。我们可以看到,除了几个指针变量外,没有使用额外的数组或栈空间,是原地算法。
二、 链表排序 (Sort List)
在数组排序中,快速排序通常是首选。但在链表中,由于无法随机访问(无法 O(1) 获取中间元素),快速排序的性能会大打折扣。因此,归并排序 (Merge Sort) 是链表排序的最佳拍档。
1. 核心思路:分治法 (Divide and Conquer)
归并排序的核心就三步:
-
找中点 (Cut):把链表从中间切断,分成左右两半。
-
递归 (Sort):对左右两半分别进行排序。
-
合并 (Merge):将两个有序的链表合并成一个有序链表。
2. 代码解析
C++代码实现:
cpp
class Solution {
// 辅助函数1:找中点并断开链表
ListNode* getMidNode(ListNode* head) {
ListNode* slow = head;
ListNode* fast = head;
ListNode* pre = nullptr; // 用于记录中点的前一个节点,方便断链
// 快慢指针找中点
while(fast && fast->next) {
pre = slow;
slow = slow->next;
fast = fast->next->next;
}
// 关键操作:断开链表!
// 如果不断开,这就不是分治,而是死循环
if (pre != nullptr) {
pre->next = nullptr;
}
return slow; // slow 就是后半段的头
}
// 辅助函数2:合并两个有序链表 (双指针拉拉链)
ListNode* merge(ListNode* l1, ListNode* l2) {
ListNode dummy(0);
ListNode* cur = &dummy;
while (l1 && l2) {
if (l1->val < l2->val) {
cur->next = l1;
l1 = l1->next;
} else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
// 接上剩余的部分
cur->next = l1 ? l1 : l2;
return dummy.next;
}
public:
ListNode* sortList(ListNode* head) {
// 递归终止条件:链表为空或只有一个节点
if (head == nullptr || head->next == nullptr) {
return head;
}
// 1. 分:找到中点,head 是前半段,head2 是后半段
ListNode* head2 = getMidNode(head);
// 2. 治:递归排序左右两半
head = sortList(head);
head2 = sortList(head2);
// 3. 合:合并两个有序链表
return merge(head, head2);
}
};3. 细节剖析
-
找中点技巧:使用快慢指针(Slow/Fast Pointers)。快指针一次走两步,慢指针一次走一步。当快指针走到头时,慢指针刚好在中间。
-
断链操作 :在
getMidNode中,我们需要维护一个pre指针指向慢指针的前一个节点。找到中点后,执行pre->next = nullptr。这一步至关重要,它将大链表物理上拆分成了两个独立的链表,否则递归无法收敛。 -
Base Case :
if (head == nullptr || head->next == nullptr)。这是递归的出口,当链表被拆解成单个节点时,单个节点天然就是有序的。
4. 复杂度分析
-
时间复杂度:O(N log N)。
-
分治的过程就像一棵二叉树,层数为 log N。
-
每一层合并操作需要遍历所有节点,耗时 N。
-
总耗时为 N * log N。
-
-
空间复杂度:O(log N)。
-
虽然我们没有申请数组,但是递归调用需要使用系统栈。
-
栈的深度取决于递归的层数,也就是链表切分的次数,即 log N。
-
注:如果采用自底向上的迭代式归并排序,空间复杂度可以优化到 O(1),但代码可读性会变差,递归写法通常是标准解法。
-
三、 总结
这两道题目代表了链表操作的两个高峰:
-
K个一组翻转 :考验的是局部操作与整体连接 的协调能力。通过引入
p0指针,我们将复杂的切分和重连问题转化为了标准的"反转+缝合"流程。 -
链表排序 :考验的是分治思想在链表上的落地。通过快慢指针解决切分问题,通过递归解决排序问题,这是解决复杂链表问题的通用模板。
掌握了这两个"大杀器",再回头看普通的链表反转或合并,就会觉得游刃有余了。