[优选算法专题八.分治-归并 ——NO.46~48 归并排序 、数组中的逆序对、计算右侧小于当前元素的个数]

题目链接

排序数组

题目描述

题目解析

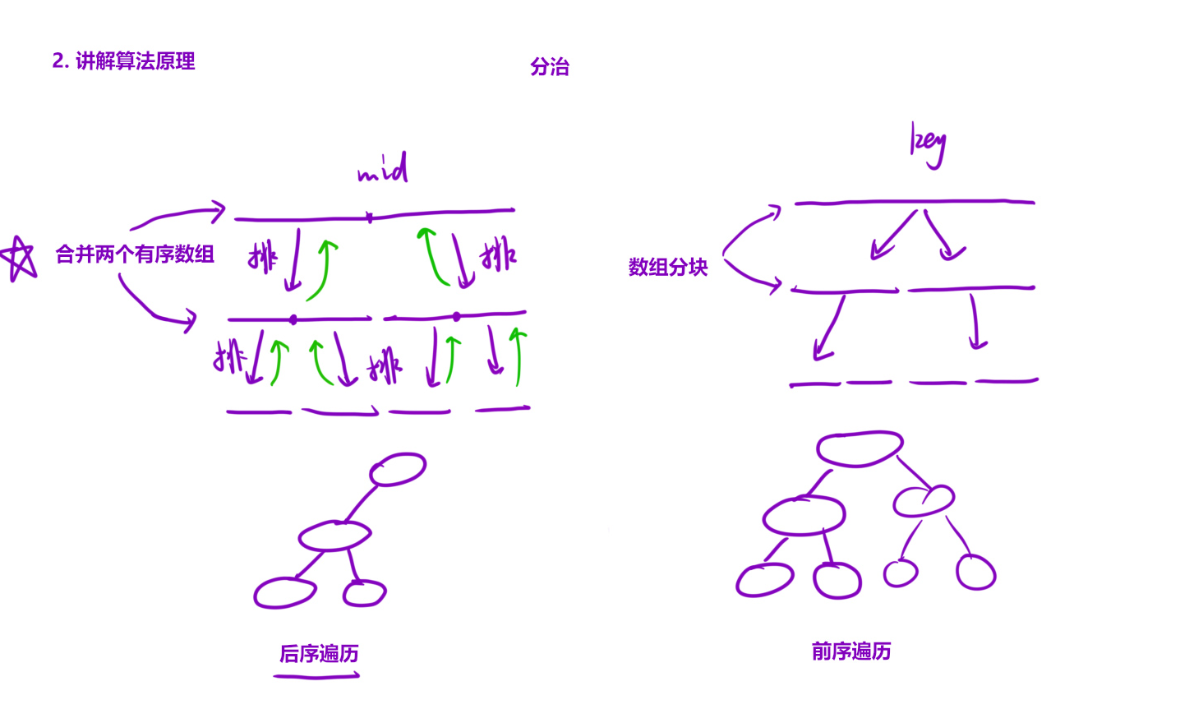
总体功能概述

这是一个 C++ 类 Solution，其中包含了一个公开方法 sortArray 和两个私有辅助方法 mergeSort 和 merge。整体功能是通过归并排序算法，将输入的整数向量 nums 原地排序并返回。

逐段逻辑解析

1. sortArray 方法

vector<int> sortArray(vector<int>& nums) 
{
    if(nums.empty()) return nums; // 边界条件：空数组直接返回
    vector<int> temp(nums.size()); // 创建临时数组，用于归并时暂存数据
    mergeSort(nums,temp,0,nums.size()-1); // 调用归并排序的递归入口
    return nums; // 返回排序后的数组
}

• 这是排序的入口方法。
• 首先处理边界情况：如果数组为空，则直接返回。
• 创建一个与原数组大小相同的临时数组 temp，避免在递归过程中频繁创建和销毁数组，提升效率。
• 调用核心的递归排序函数 mergeSort，传入数组、临时数组以及排序范围（从索引 0 到最后一个元素）。

2. mergeSort 方法（递归分解）

void mergeSort(vector<int>& nums,vector<int>& temp,int left,int right)
{
    if(left>=right)return; // 递归终止条件：子数组只有一个元素或为空
    int mid=left+(right-left)/2; // 计算中间点，避免溢出（优于 (left+right)/2）

    mergeSort(nums,temp,left,mid); // 递归排序左半部分 [left, mid]
    mergeSort(nums,temp,mid+1,right); // 递归排序右半部分 [mid+1, right]

    merge(nums,temp,left,mid,right); // 合并两个已排序的子数组
}

• 这是归并排序的核心递归函数，遵循分治法 (Divide and Conquer) 思想。
• 终止条件 ：当 left >= right 时，子数组长度为 1 或 0，天然有序，直接返回。
• 分解 (Divide) ：计算中间索引 mid，将数组分为左右两部分。
• 解决 (Conquer)：递归地对左右两个子数组分别进行排序。
• 合并 (Combine) ：调用 merge 方法，将两个已排序的子数组合并为一个有序数组。

3. merge 方法（合并有序数组）

void merge(vector<int>& nums,vector<int>& temp,int left,int mid,int right)
{
    int i=left; // 左子数组的起始指针
    int j=mid+1; // 右子数组的起始指针
    int k=left; // 临时数组的写入指针

    // 双指针遍历，比较左右子数组元素，将较小的元素放入临时数组
    while(i<=mid && j<=right)
    {
        if(nums[i]<=nums[j])
        {
            temp[k++]=nums[i++];
        }
        else
        {
            temp[k++]=nums[j++];
        }
    }

    // 处理左子数组的剩余元素
    while(i<=mid)
    {
        temp[k++]=nums[i++];
    }
    // 处理右子数组的剩余元素
    while(j<=right)
    {
        temp[k++]=nums[j++];
    }

    // 将临时数组中已排序的部分复制回原数组
    for(i=left;i<=right;i++)
    {
        nums[i]=temp[i];
    }
}

• 这是归并排序的合并操作，负责将两个已排序的子数组（[left, mid] 和 [mid+1, right]）合并为一个有序数组。
• 使用三个指针：i 遍历左子数组，j 遍历右子数组，k 指向临时数组的写入位置。
• 第一步：双指针比较，将较小的元素依次放入临时数组，直到其中一个子数组遍历完毕。
• 第二步：将未遍历完的子数组的剩余元素直接追加到临时数组末尾。
• 第三步：将临时数组中合并好的有序数据复制回原数组的对应位置，完成合并。

输入与输出分析

• 输入 ：一个整数向量 nums（可能无序）。
• 输出：排序后的整数向量（升序排列）。
• 算法特性：
  • 时间复杂度：O (n log n)，分解过程是对数级，合并过程是线性级。
  • 空间复杂度 ：O (n)，主要来自于临时数组 temp。
  • 稳定性：稳定排序（相等元素的相对顺序保持不变）。

总结

• 归并排序的核心是分治法：先递归分解数组，再合并有序子数组。
• mergeSort 负责递归分解，merge 负责合并两个有序子数组，是算法的关键操作。
• 该算法的优点是时间复杂度稳定且为 O (n log n)，缺点是需要额外的 O (n) 空间。

---

题目链接

数组中的逆序对

题目描述

题目解析

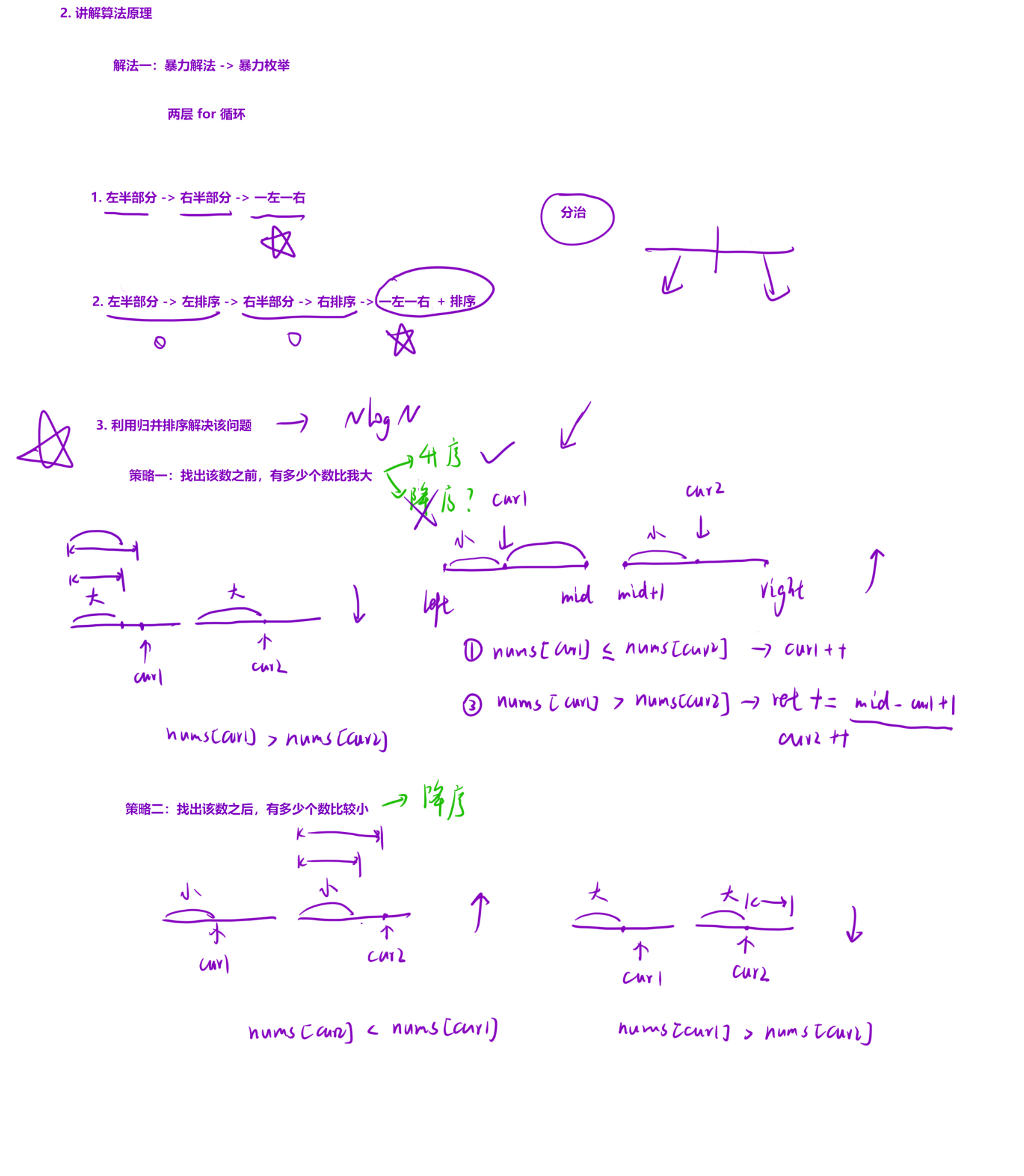
总体功能概述

这段代码实现了一个高效计算数组中逆序对总数的算法。它利用归并排序 的分治思想，在排序的过程中同步统计逆序对的数量，时间复杂度为 O(n log n)， 远优于暴力枚举的 O(n^2)。

逐段代码解析

1. 主函数 reversePairs

int reversePairs(vector<int>& record) {
    if (record.empty()) return 0;
    vector<int> temp(record.size()); // 辅助数组，避免频繁创建销毁
    return mergeSort(record, temp, 0, record.size() - 1);
}

• 功能：这是算法的入口函数。
• 逻辑 ：
  • 首先检查输入数组是否为空，如果为空则直接返回 0（没有逆序对）。
  • 创建一个与输入数组大小相同的辅助数组 temp，用于在合并过程中暂存数据，避免频繁的内存分配和释放。
  • 调用核心递归函数 mergeSort，传入原数组、辅助数组、数组的左右边界索引（0 和 size-1），并返回最终统计的逆序对总数。

2. 递归分治函数 mergeSort

int mergeSort(vector<int>& nums, vector<int>& temp, int left, int right) {
    if (left >= right) return 0;
    
    int mid = left + (right - left) / 2;
    int count = 0;
    
    // 分治：计算左右子数组的逆序对
    count += mergeSort(nums, temp, left, mid);
    count += mergeSort(nums, temp, mid + 1, right);
    
    // 合并：计算跨区间的逆序对
    count += merge(nums, temp, left, mid, right);
    
    return count;
}

• 功能：将数组递归地分割成子数组，并合并子数组以统计逆序对。
• 逻辑 ：
  • 递归终止条件 ：当 left >= right 时，子数组只有一个元素或为空，没有逆序对，返回 0。
  • 分割 ：计算中间索引 mid，将数组分为左半部分 [left, mid] 和右半部分 [mid+1, right]。
  • 递归处理 ：分别递归处理左、右子数组，将返回的逆序对数量累加到 count。
  • 合并 ：调用 merge 函数合并两个已排序的子数组，并统计跨越两个子数组的逆序对数量，累加到 count。
  • 返回当前子数组的总逆序对数量。

3. 合并与统计函数 merge

int merge(vector<int>& nums, vector<int>& temp, int left, int mid, int right) {
    int i = left;    // 左子数组指针
    int j = mid + 1; // 右子数组指针
    int k = left;    // 辅助数组指针
    int count = 0;

    // 合并两个有序子数组并统计逆序对
    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j]) {
            temp[k++] = nums[i++];
        } else {
            temp[k++] = nums[j++];
            // 左子数组中 i 到 mid 的所有元素都与 nums[j] 构成逆序对
            count += (mid - i + 1);
        }
    }

    // 处理剩余元素
    while (i <= mid) {
        temp[k++] = nums[i++];
    }
    while (j <= right) {
        temp[k++] = nums[j++];
    }

    // 将辅助数组的内容复制回原数组
    for (k = left; k <= right; ++k) {
        nums[k] = temp[k];
    }

    return count;
}

• 功能：合并两个已排序的子数组，并统计跨区间的逆序对数量。
• 逻辑 ：

  • 初始化指针：

    • i：指向左子数组的起始位置 left。
    • j：指向右子数组的起始位置 mid+1。
    • k：指向辅助数组 temp 的起始位置 left。
    • count：用于统计当前合并过程中的逆序对数量。

  • 核心合并与统计循环：

    • 当 i 和 j 都未越界时，比较 nums[i] 和 nums[j]：
      • 如果 nums[i] <= nums[j]：说明当前元素顺序正确，将 nums[i] 放入 temp，并移动 i 和 k。
      • 如果 nums[i] > nums[j]：说明 nums[j] 与左子数组中从 i 到 mid 的所有元素都构成逆序对（因为左子数组已排序），所以逆序对数量增加 mid - i + 1，然后将 nums[j] 放入 temp，并移动 j 和 k。

  • 处理剩余元素：

    • 左子数组可能还有剩余元素，将其全部复制到 temp。
    • 右子数组可能还有剩余元素，将其全部复制到 temp。

  • 复制回原数组 ：将辅助数组 temp 中合并好的有序数据复制回原数组 nums 的对应位置 [left, right]，以保证后续递归合并时子数组是有序的。

  • 返回本次合并统计的逆序对数量。

总结

• 核心思想 ：利用归并排序的分治特性，在合并有序子数组时高效统计逆序对，避免了暴力枚举的高时间复杂度。
• 关键操作 ：合并时，若左子数组元素大于右子数组元素，则左子数组剩余所有元素均与当前右子数组元素构成逆序对，直接计算数量 mid - i + 1。
• 复杂度 ：时间复杂度为O(n log n) （归并排序的时间），空间复杂度为O(n)（辅助数组的空间）。

思考，如果是求升序对呢❓

全局升序对指数组中所有满足 i <j 且 nums [i] < nums [j] 的元素对。例如，数组 [9, 7, 5, 4, 6] 的全局升序对有 (5, 6)、(4, 6)，总数为 2。

思路：归并排序适配法

与统计全局逆序对的思路对称，我们可以在归并排序的合并阶段统计升序对：

#include <vector>
#include <iostream>
using namespace std;

class Solution {
public:
    int countGlobalAscendingPairs(vector<int>& record) {
        if (record.empty()) return 0;
        vector<int> temp(record.size());
        return mergeSort(record, temp, 0, record.size() - 1);
    }

private:
    int mergeSort(vector<int>& nums, vector<int>& temp, int left, int right) {
        if (left >= right) return 0;
        
        int mid = left + (right - left) / 2;
        int count = 0;
        
        // 分治：统计左右子数组的升序对
        count += mergeSort(nums, temp, left, mid);
        count += mergeSort(nums, temp, mid + 1, right);
        
        // 合并：统计跨区间的升序对
        count += merge(nums, temp, left, mid, right);
        
        return count;
    }

    int merge(vector<int>& nums, vector<int>& temp, int left, int mid, int right) {
        int i = left;    // 左子数组指针
        int j = mid + 1; // 右子数组指针
        int k = left;    // 辅助数组指针
        int count = 0;

        // 合并两个有序子数组并统计升序对
        while (i <= mid && j <= right) {
            if (nums[i] < nums[j]) {
                temp[k++] = nums[i++];
                // 右子数组中 j 到 right 的所有元素都与 nums[i-1] 构成升序对
                count += (right - j + 1);
            } else {
                temp[k++] = nums[j++];
            }
        }

        // 处理剩余元素
        while (i <= mid) {
            temp[k++] = nums[i++];
        }
        while (j <= right) {
            temp[k++] = nums[j++];
        }

        // 将辅助数组内容复制回原数组
        for (k = left; k <= right; ++k) {
            nums[k] = temp[k];
        }

        return count;
    }
};

核心逻辑对比

|-----------|-----------------------------------|--------------------------------------|
| 统计类型 | 条件 | 统计关键点 |
| 全局逆序对 | nums[i] > nums[j] (i<j) | 左子数组元素 > 右子数组元素时，统计 mid-i+1 |
| 全局升序对 | nums[i] < nums[j] (i<j) | 左子数组元素 < 右子数组元素时，统计 right-j+1 |

总结

• 全局升序对 ：复用归并排序的分治思想，在合并阶段统计升序对，时间复杂度 O(n log n)，核心是当左子数组元素小于右子数组元素时，右子数组剩余所有元素都与当前左元素构成升序对。
• 升序对与逆序对的统计逻辑对称，仅需调整比较条件和统计方式即可实现。

---

题目链接

计算右侧小于当前元素的个数

题目描述

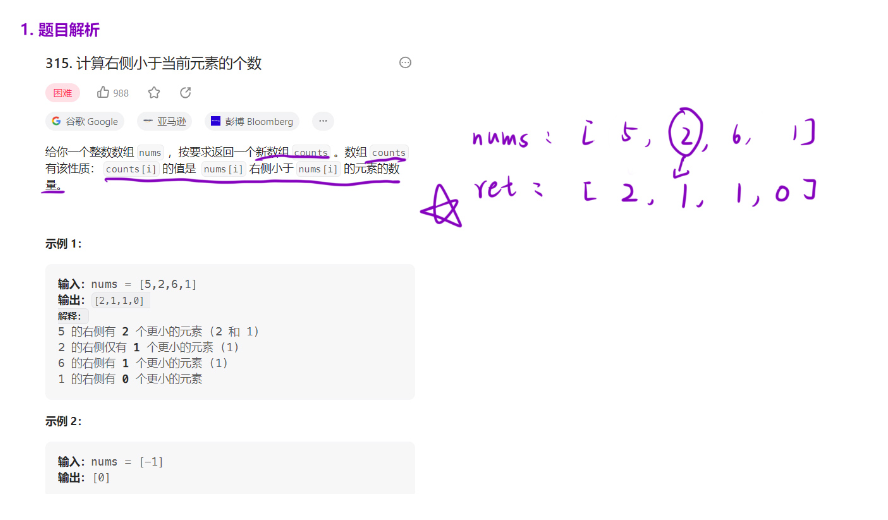
题目解析

总体功能概述

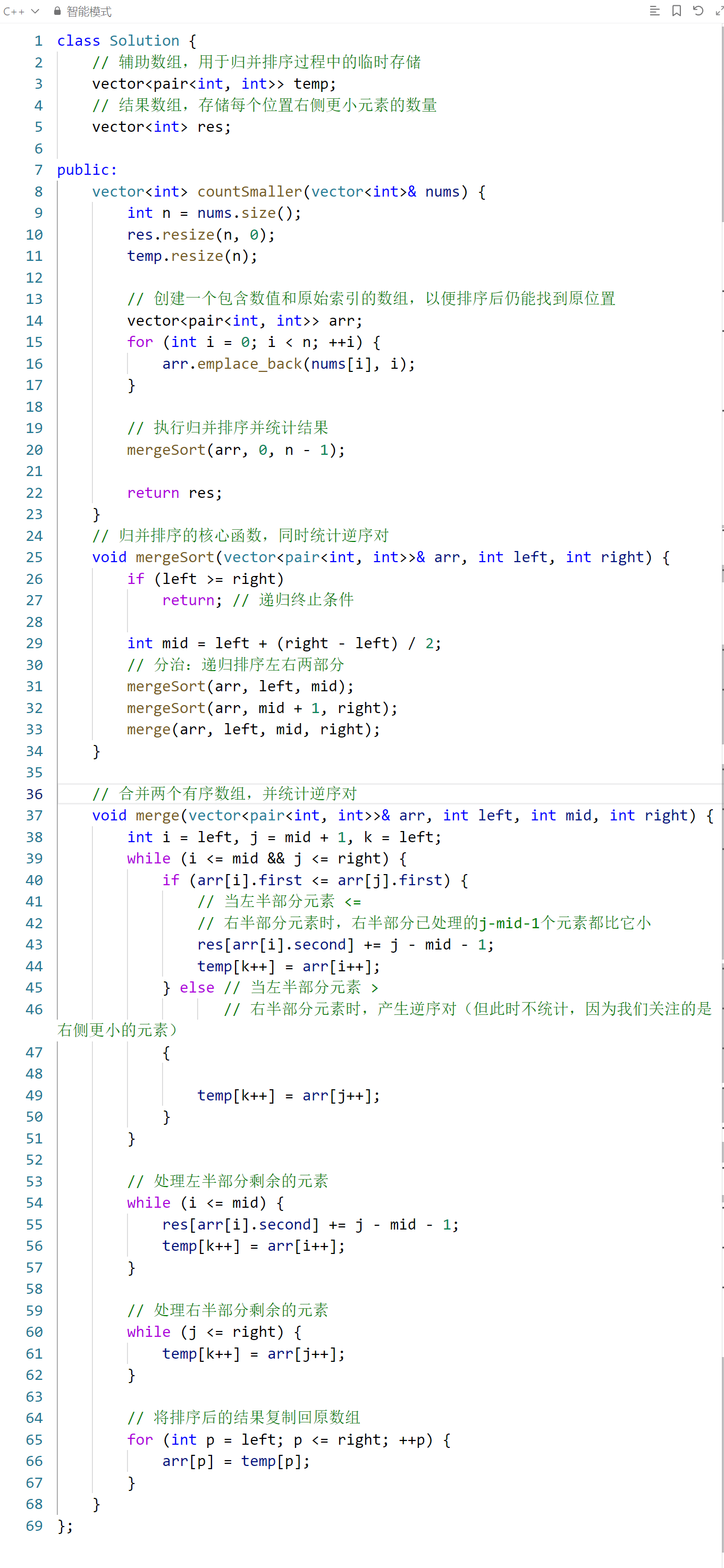
该算法通过在归并排序的合并阶段统计 "逆序对" 的数量，来得到每个元素右侧比它小的元素个数。时间复杂度为 O (n log n)，空间复杂度为 O (n)，相比暴力法 O (n²) 的时间复杂度有显著提升。

核心逻辑解析

1. 数据结构设计

// 辅助数组，用于归并排序过程中的临时存储
vector<pair<int, int>> temp;
// 结果数组，存储每个位置右侧更小元素的数量
vector<int> res;

// 创建一个包含数值和原始索引的数组
vector<pair<int, int>> arr;
for (int i = 0; i < n; ++i) {
    arr.emplace_back(nums[i], i);
}

• 使用pair<int, int> 来保存数值 和它的原始索引，这样在排序打乱顺序后，依然能找到每个元素在原数组中的位置。
• temp数组用于归并排序的合并阶段临时存储数据。
• res 数组存储最终结果，res[i] 表示原数组第i个元素右侧比它小的元素个数。

2. 归并排序主函数

void mergeSort(vector<pair<int, int>>& arr, int left, int right) {
    if (left >= right)
        return; // 递归终止条件

    int mid = left + (right - left) / 2;
    mergeSort(arr, left, mid);    // 排序左半部分
    mergeSort(arr, mid + 1, right); // 排序右半部分
    merge(arr, left, mid, right); // 合并并统计
}

• 采用标准的分治策略，将数组不断二分，直到子数组长度为 1。
• 在合并阶段完成核心的统计工作。

3. 合并与统计的核心逻辑

while (i <= mid && j <= right) {
    if (arr[i].first <= arr[j].first) {
        // 关键：统计右侧比当前元素小的个数
        res[arr[i].second] += j - mid - 1;
        temp[k++] = arr[i++];
    } else {
        temp[k++] = arr[j++];
    }
}

// 处理左半部分剩余元素
while (i <= mid) {
    res[arr[i].second] += j - mid - 1;
    temp[k++] = arr[i++];
}

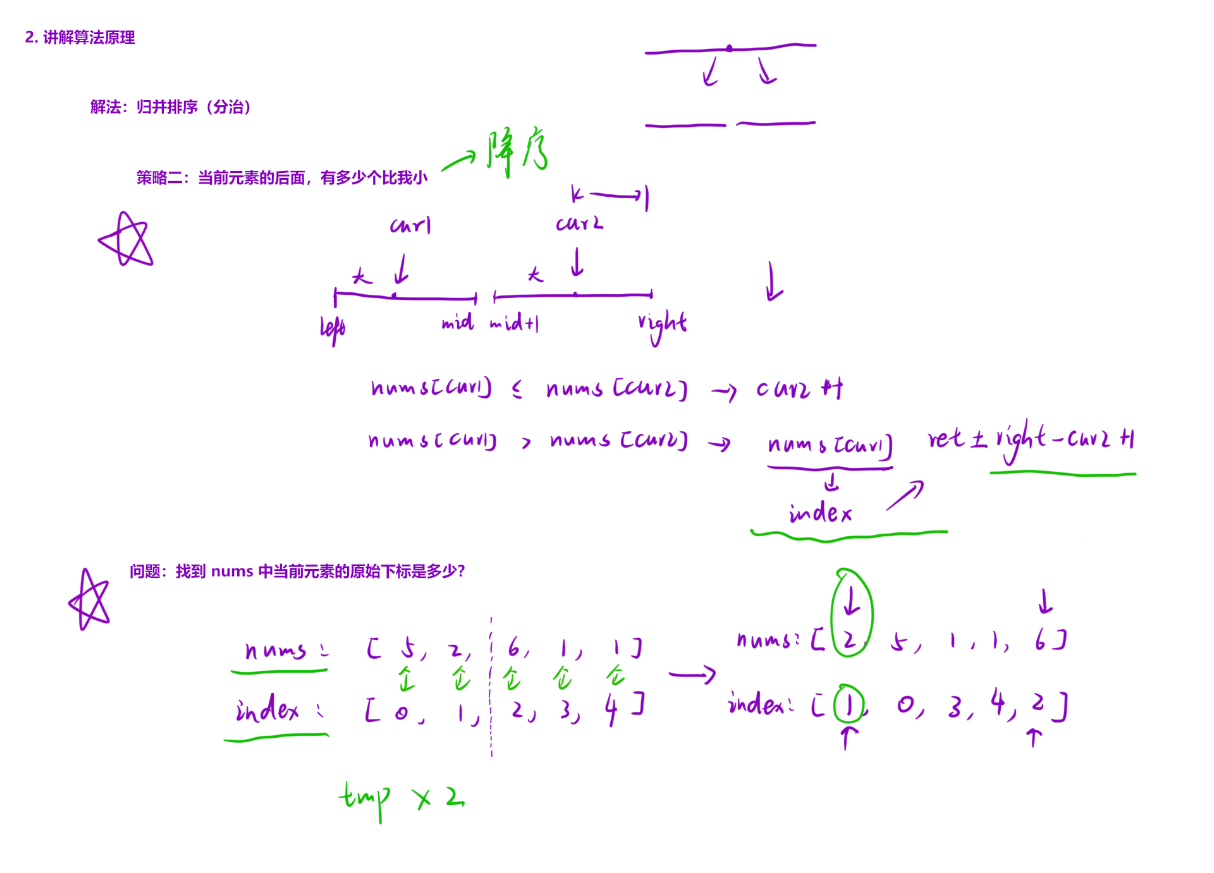
这是整个算法的精髓所在：

• 当arr[i].first <= arr[j].first 时，说明右半部分中从mid+1 到j-1 的所有元素（共j-mid-1 个）都比**arr[i]**小。
• 因此，我们将这个数量累加到**res[arr[i].second]**中（通过原始索引定位）。
• 即使左半部分有剩余元素，它们也都比右半部分所有元素大，所以要加上右半部分的总长度。

执行流程示例

假设输入数组为 [5, 2, 6, 1]：

1. 初始arr = [(5,0), (2,1), (6,2), (1,3)]
2. 归并排序分解为[(5,0), (2,1)]和[(6,2), (1,3)]
3. 合并[(5,0), (2,1)]时：
   • 5 > 2，所以res[0] += 1（5 右侧有 1 个更小的元素）
4. 合并[(6,2), (1,3)]时：
   • 6 > 1，所以res[2] += 1（6 右侧有 1 个更小的元素）
5. 最后合并两个有序子数组[(2,1), (5,0)]和[(1,3), (6,2)]：
   • 2 > 1，直接放入 1
   • 2 <= 6，res[1] += 1（2 右侧有 1 个更小的元素）
   • 5 <= 6，res[0] += 2（5 右侧有 2 个更小的元素）
6. 最终结果res = [2, 1, 1, 0]

总结

• 核心思想：利用归并排序的合并阶段，在比较元素大小时顺带统计右侧更小元素的数量。
• 关键技巧 ：使用pair保存元素值和原始索引，确保排序后能正确更新结果数组。
• 复杂度优势：时间复杂度 O (n log n)，空间复杂度 O (n)，是解决此类逆序对问题的最优方法之一。