文章目录
- [一. 力扣 912. 排序数组](#一. 力扣 912. 排序数组)
-
- [1. 题目](#1. 题目)
- [2. 算法原理](#2. 算法原理)
- 3.代码
- [二. 力扣 LCR 170. 交易逆序对的总数](#二. 力扣 LCR 170. 交易逆序对的总数)
-
- [1. 题目](#1. 题目)
- [2. 算法原理](#2. 算法原理)
-
- [(1) 方法一](#(1) 方法一)
- [(2) 方法二](#(2) 方法二)
- [3. 代码](#3. 代码)
-
- [(1) 方法一代码:](#(1) 方法一代码:)
- [(2) 方法二代码:](#(2) 方法二代码:)
- [三. 力扣 315. 计算右侧小于当前元素的个数](#三. 力扣 315. 计算右侧小于当前元素的个数)
-
- [1. 题目](#1. 题目)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [四. 力扣 493. 翻转对](#四. 力扣 493. 翻转对)
-
- [1. 题目](#1. 题目)
- [2. 算法原理](#2. 算法原理)
-
- [(1) 方法一(降序):](#(1) 方法一(降序):)
- [(2) 方法二(升序):](#(2) 方法二(升序):)
- [3. 代码](#3. 代码)
-
- [(1) 方法一(降序)代码:](#(1) 方法一(降序)代码:)
- [(2) 方法二(升序)代码:](#(2) 方法二(升序)代码:)
这个篇章我们基于归并排序,并结合分治思想来解决问题
一. 力扣 912. 排序数组
1. 题目
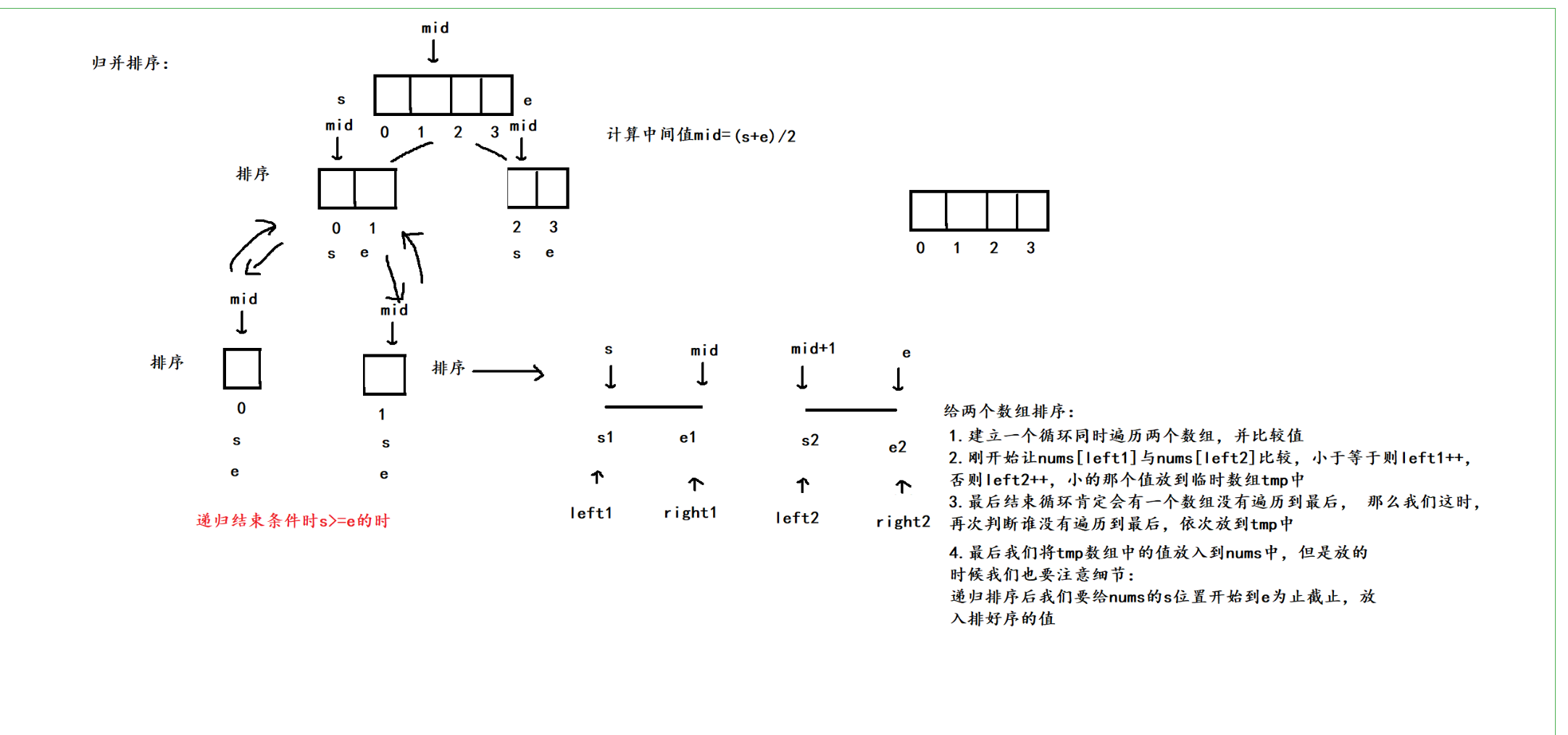
2. 算法原理
归并排序我们应该不陌生, 这里我们只是复习归并排序的算法原理
3.代码
java
public int[] sortArray(int[] nums) {
mergeSort(nums,0,nums.length-1);
return nums;
}
public void mergeSort(int[] nums, int s, int e) {
if (s >= e) {
return;
}
int mid = (s + e) / 2;
// 递归左区间
mergeSort(nums,s,mid);
// 递归右区间
mergeSort(nums,mid + 1,e);
// 递归完成后, 给两个数组排序(数组并不是真实数组,而是可以看成两个数组)
int left1 = s;
int left2 = mid + 1;
int i = 0;
int[] tmp = new int[e - s + 1];
while (left1 <= mid && left2 <= e) {
if (nums[left1] <= nums[left2]) {
tmp[i++] = nums[left1++];
}else {
tmp[i++] = nums[left2++];
}
}
while(left1 <= mid) {
tmp[i++] = nums[left1++];
}
while(left2 <= e) {
tmp[i++] = nums[left2++];
}
// 将tmp数组的值放入nums中
for (int j = 0; j < e - s + 1; j++) {
nums[j + s] = tmp[j];
}
}二. 力扣 LCR 170. 交易逆序对的总数
1. 题目
2. 算法原理
(1) 方法一
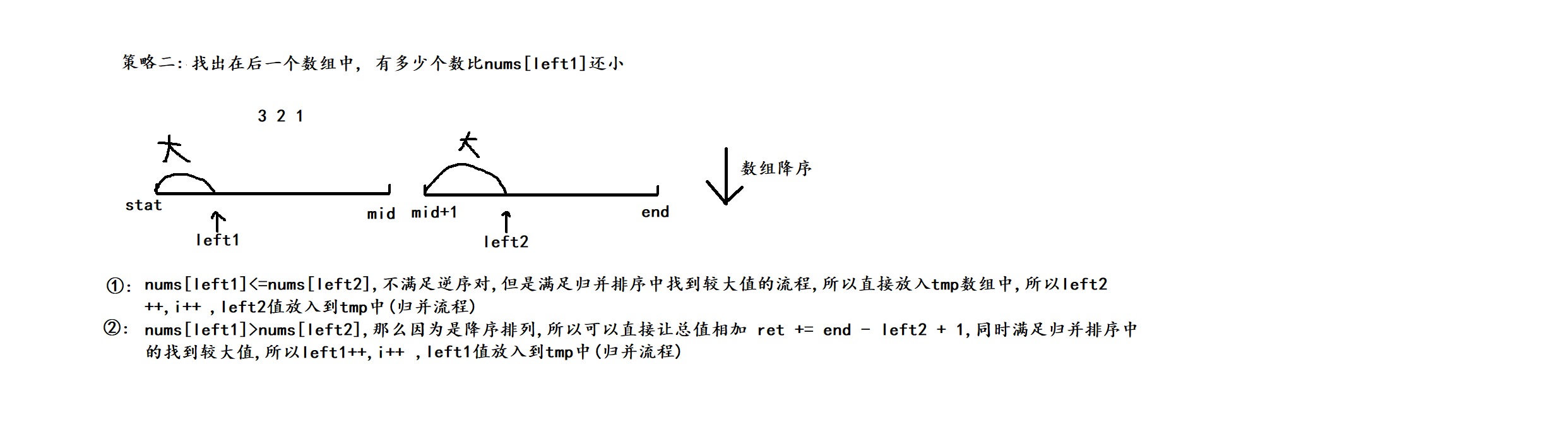
(2) 方法二
3. 代码
(1) 方法一代码:
java
int ret = 0;
int[] tmp ;
public int reversePairs(int[] nums) {
tmp = new int[nums.length];
mergeSort(nums, 0,nums.length - 1);
return ret;
}
public void mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int mid = (end + start) / 2;
// 递归左面[s,mid]
mergeSort(nums, start, mid);
// 递归右面[mid+1,e]
mergeSort(nums, mid + 1, end);
// 递归结束, 开始排序, 并统计
int left1 = start;
int left2 = mid + 1;
int i = 0;
while (left1 <= mid && left2 <= end) {
if (nums[left1] <= nums[left2]) {
tmp[i++] = nums[left1++];
}else {
ret += mid - left1 + 1;
tmp[i++] = nums[left2++];
}
}
while (left1 <= mid) {
tmp[i++] = nums[left1++];
}
while (left2 <= end) {
tmp[i++] = nums[left2++];
}
for (int j = 0; j < end - start + 1; j++) {
nums[j + start] = tmp[j];
}
}(2) 方法二代码:
java
int ret = 0;
int[] tmp ;
public int reversePairs(int[] nums) {
tmp = new int[nums.length];
mergeSort(nums, 0,nums.length - 1);
return ret;
}
public void mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int mid = (end + start) / 2;
// 递归左面[s,mid]
mergeSort(nums, start, mid);
// 递归右面[mid+1,e]
mergeSort(nums, mid + 1, end);
// 递归结束, 开始排序, 并统计
int left1 = start;
int left2 = mid + 1;
int i = 0;
while (left1 <= mid && left2 <= end) {
if (nums[left1] <= nums[left2]) {
tmp[i++] = nums[left2++];
}else {
ret += end - left2 + 1;
tmp[i++] = nums[left1++];
}
}
while (left1 <= mid) {
tmp[i++] = nums[left1++];
}
while (left2 <= end) {
tmp[i++] = nums[left2++];
}
for (int j = 0; j < end - start + 1; j++) {
nums[j + start] = tmp[j];
}
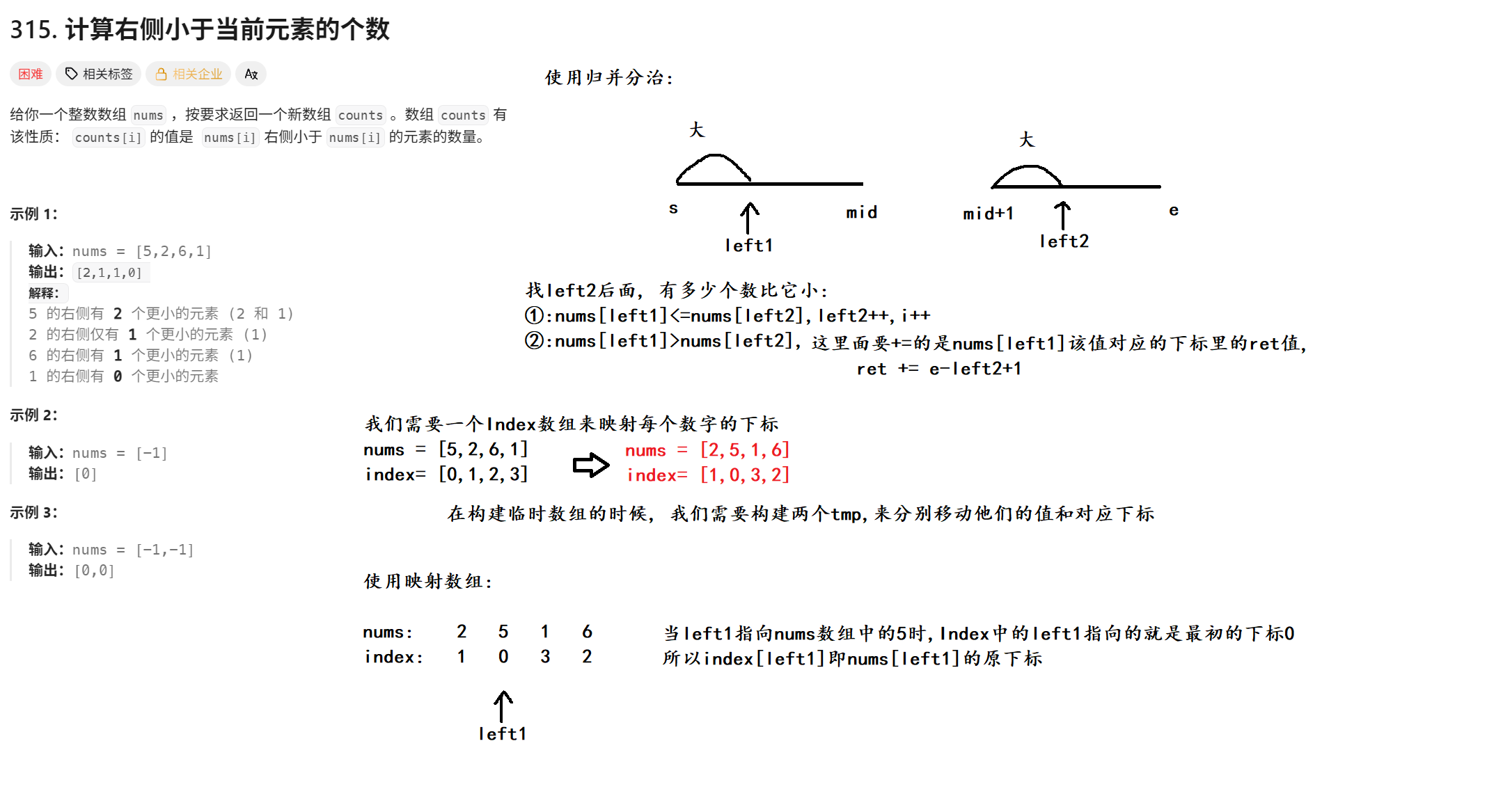
}三. 力扣 315. 计算右侧小于当前元素的个数
1. 题目
2. 算法原理
3. 代码
java
int[] tmpNums;
int[] tmpIndex;
int[] index;
int[] ret;
public List<Integer> countSmaller(int[] nums) {
List<Integer> list = new ArrayList<>();
int n = nums.length;
tmpNums = new int[n];
tmpIndex = new int[n];
index = new int[n];
ret = new int[n];
for (int i = 0; i < n; i++) {
index[i] = i;
}
mergeSort(nums, 0, n - 1);
for (int x : ret) {
list.add(x);
}
return list;
}
public void mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int mid = (start + end) / 2;
// 计算左面个数
mergeSort(nums, start, mid);
// 计算右面个数
mergeSort(nums, mid + 1, end);
// 计算一左一右
int left1 = start;
int left2 = mid + 1;
int i = 0;
while (left1 <= mid && left2 <= end) {
if (nums[left1] <= nums[left2]) {
tmpNums[i] = nums[left2];
tmpIndex[i++] = index[left2++];
}else {
ret[index[left1]] += end - left2 + 1;
tmpNums[i] = nums[left1];
tmpIndex[i++] = index[left1++];
}
}
while (left1 <= mid) {
tmpNums[i] = nums[left1];
tmpIndex[i++] = index[left1++];
}
while (left2 <= end) {
tmpNums[i] = nums[left2];
tmpIndex[i++] = index[left2++];
}
// 将tmp数组的值放回到原数组其中, 排序工作
for (int j = start; j <= end; j++) {
nums[j] = tmpNums[j - start];
index[j] = tmpIndex[j - start];
}
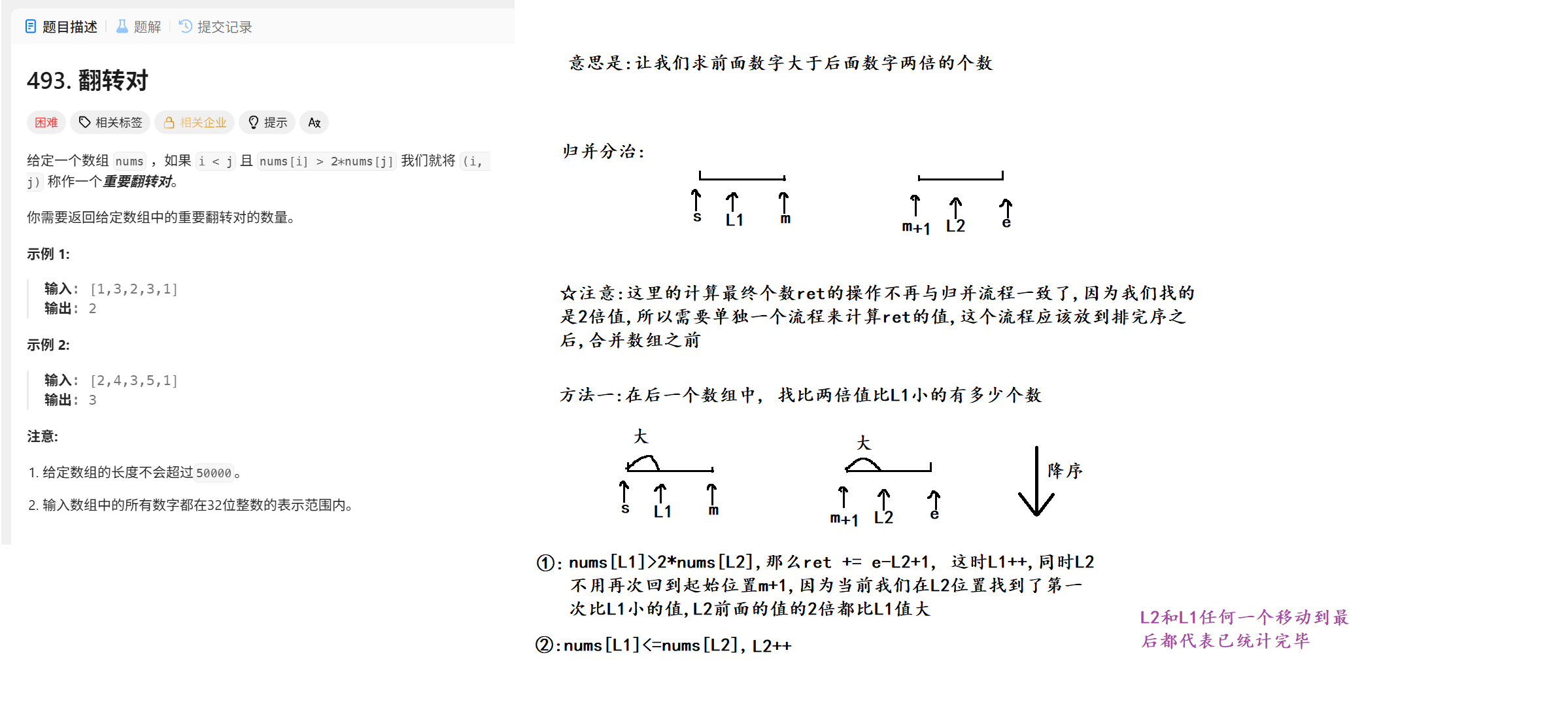
}四. 力扣 493. 翻转对
1. 题目
题目意思大白话解释就是前面有多少数大于后面数值的2倍
2. 算法原理
(1) 方法一(降序):
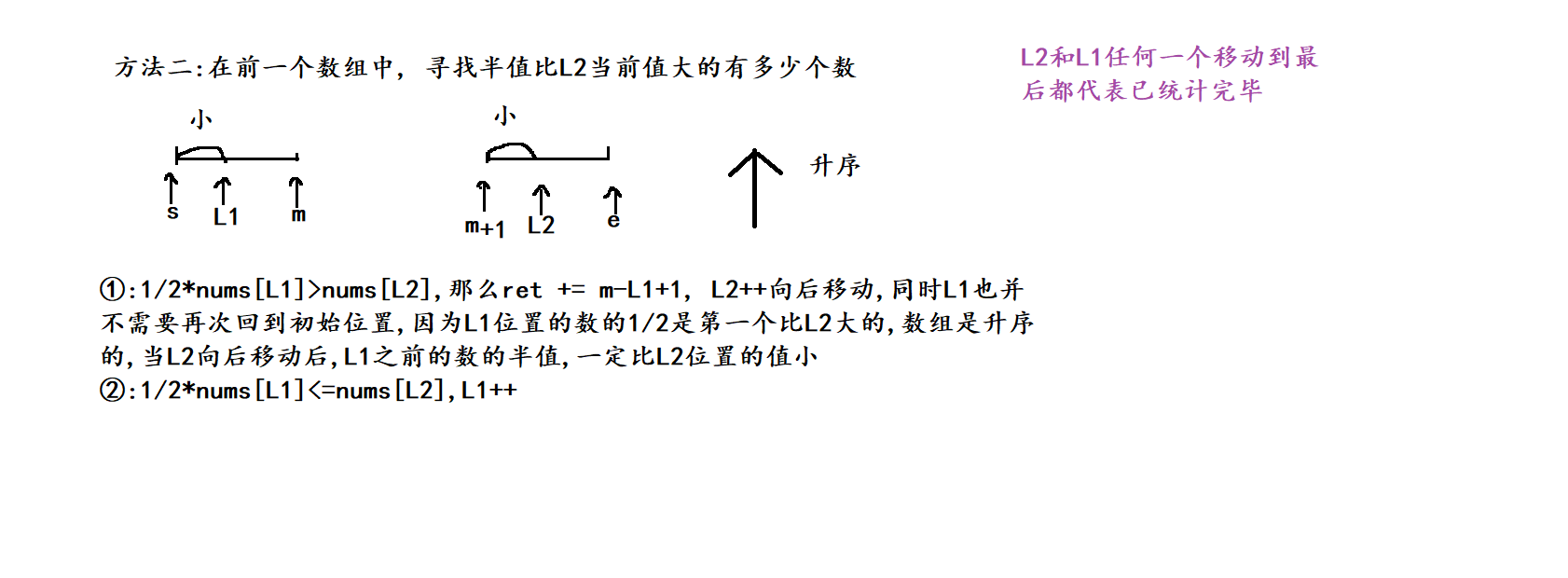
(2) 方法二(升序):
3. 代码
(1) 方法一(降序)代码:
我们要注意,这道题里面的测试用例输入数组中的所有数字都在32位整数的表示范围内, 但是我们×2后那么就会超出32位, 所以我们用除以2的方式
java
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums, 0, n - 1);
}
public int mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return 0;
}
int ret = 0;
int mid = (start + end) / 2;
// 先计算左面
ret += mergeSort(nums, start, mid);
// 再计算右面
ret += mergeSort(nums, mid + 1, end);
// 最后计算一左一右
int left1 = start;
int left2 = mid + 1;
while (left1 <= mid && left2 <= end) {
if (nums[left1] / 2.0 > nums[left2]) {
ret += end - left2 + 1;
left1++;
}else {
left2++;
}
}
// 放入tmp中排序
left1 = start;
left2 = mid + 1;
int i = 0;
while (left1 <= mid && left2 <= end) {
tmp[i++] = nums[left1] > nums[left2] ? nums[left1++] : nums[left2++];
}
while (left1 <= mid) {
tmp[i++] = nums[left1++];
}
while (left2 <= end) {
tmp[i++] = nums[left2++];
}
// 合并数组
for (int j = start; j <= end; j++) {
nums[j] = tmp[j - start];
}
return ret;
}(2) 方法二(升序)代码:
java
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums, 0, n - 1);
}
public int mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return 0;
}
int ret = 0;
int mid = (start + end) / 2;
// 先计算左面
ret += mergeSort(nums, start, mid);
// 再计算右面
ret += mergeSort(nums, mid + 1, end);
// 最后计算一左一右
int left1 = start;
int left2 = mid + 1;
while (left1 <= mid && left2 <= end) {
if (nums[left1] / 2.0 > nums[left2]) {
ret += mid - left1 + 1;
left2++;
}else {
left1++;
}
}
// 放入tmp中排序
left1 = start;
left2 = mid + 1;
int i = 0;
while (left1 <= mid && left2 <= end) {
tmp[i++] = nums[left1] <= nums[left2] ? nums[left1++] : nums[left2++];
}
while (left1 <= mid) {
tmp[i++] = nums[left1++];
}
while (left2 <= end) {
tmp[i++] = nums[left2++];
}
// 合并数组
for (int j = start; j <= end; j++) {
nums[j] = tmp[j - start];
}
return ret;
}