目录
[(1)第一次分配:创建 "行指针数组"(书架)](#(1)第一次分配:创建 “行指针数组”(书架))
[(2)第二次分配:为每行创建 "列数组"(书本)](#(2)第二次分配:为每行创建 “列数组”(书本))
一、问题描述
设有n=2^k个球队参加循环赛,要求设计一个满足以下要求比赛日程表: (1) 每支球队必须与其他n-1支球队各赛一次; (2) 每支球队一天只能参赛一次; (3) 循环赛在n-1天内结束。
输入:一个整数k
输出:输出一个n行n列的表,在表中的第i行,第j列处填入为第i个球队在第j天所遇到的球队。
二、核心思路:分治法
1、分析不同规模的问题,我们发现一个重要的递归模式:
当k=1时(两个球队),比赛循环赛日程表为
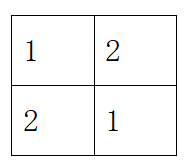
当k=2时(四个球队),循环赛日程表为
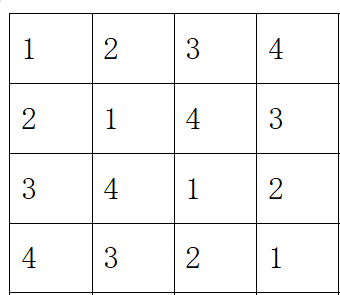
关键规律:
-
左上角子矩阵 = 右下角子矩阵
-
左下角子矩阵 = 右上角子矩阵
-
右上角子矩阵 = 左上角子矩阵 + 子矩阵大小
2、分治法的定义
分治法 (Divide and Conquer)是一种重要的算法设计思想,它将一个复杂的大问题分解 成若干个规模较小但结构与原问题相似的子问题,递归地 解决这些子问题,然后再合并子问题的解来得到原问题的解。
3、分治策略:
-
分解 :将
n×n矩阵划分为4个(n/2)×(n/2)子矩阵 -
递归求解:递归填充左上角子矩阵
-
组合:
-
右上角 = 左上角 +
n/2 -
左下角 = 右上角
-
右下角 = 左上角
-
当k=3时(八个球队),循环赛日程表为
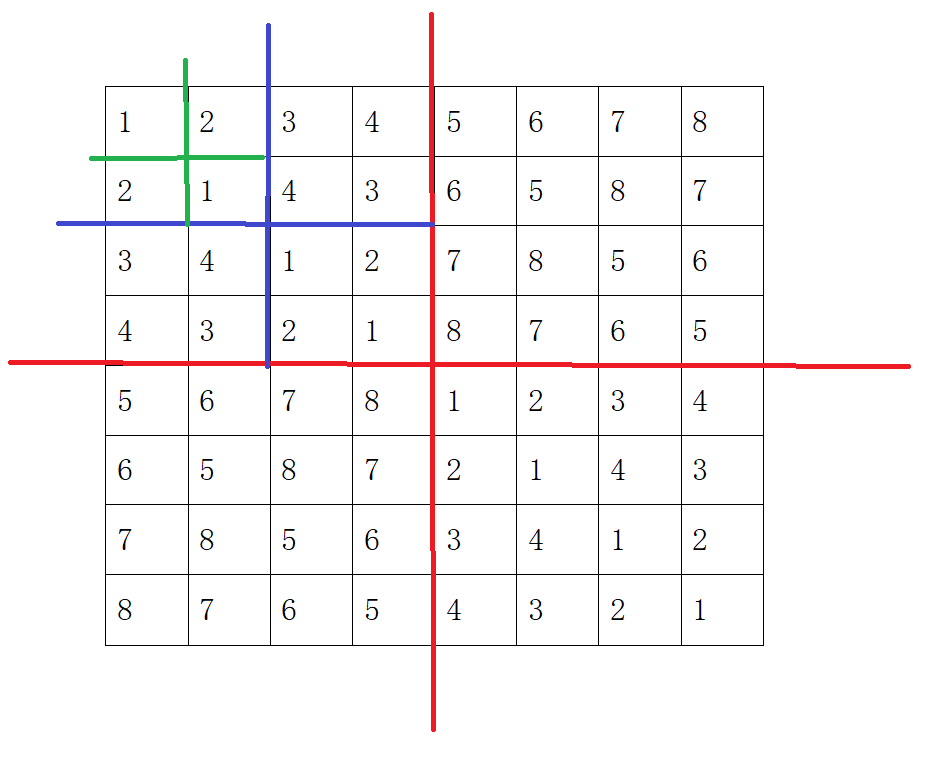
采用分治策略:将循环赛日程表划分为四个大区域(红色线划分的),再把其中一个大区域划分为四个小区域(蓝色线划分的),最后把其中的一个小区域划分为四个更小的区域(绿色线划分的)
三、算法实现
1、动态二维数组的本质:"数组的数组"
二维数组在内存中不是 "一块连续的矩形空间"(静态二维数组看似连续,但动态二维数组是 "分散的"),而是:
- 一个存储行指针的一维数组(简称 "行指针数组");
- 每个行指针再指向一个存储列数据的一维数组(简称 "列数组")。
就像 "书架" 和 "书本" 的关系:
- 第一步先造一个 "书架"(行指针数组),用来放 "书本的地址";
- 第二步再为每一层书架放一本 "书"(列数组),书里才是真正的数据。
例如:int table[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}}; 所以使用动态二维数组的实现:必须用int **
2、动态内存分配原理
由于需要处理可变大小的矩阵,我们使用动态二维数组,动态二维数组需要两次地址分配,分别为"行指针数组的分配"和"每行列空间的分配" 这两个不同的步骤。
(1)第一次分配:创建 "行指针数组"(书架)
cs
int** schedule = (int**)malloc((n + 1) * sizeof(int*));- 作用:分配一块内存,用来存储
n+1个 "指向 int 的指针"(即int*类型)。 - 对于
n=8,这一步会分配9个int*大小的空间(索引 0~8),每个位置可以存一个 "列数组的地址"。 - 此时
schedule是 "指向指针的指针"(int**),它指向这个 "行指针数组" 的首地址。
注意 :这一步只是造了 "空书架",书架上还没有 "书"(列数组),所以schedule[i]此时是随机的垃圾地址,不能直接用。
(2)第二次分配:为每行创建 "列数组"(书本)
cs
for (int i = 0; i <= n; i++) {
schedule[i] = (int*)malloc((n + 1) * sizeof(int));
}- 作用:遍历 "行指针数组" 的每个位置(
schedule[0]到schedule[n]),为每个位置分配一块内存(n+1个int大小),用来存储该行的列数据。 - 对于
n=8,这一步会循环 9 次,每次分配 9 个int大小的空间(列索引 0~8),并将这些空间的地址存入schedule[i]。 - 此时
schedule[i]才指向有效的 "列数组",我们可以通过schedule[i][j]访问第i行第j列的数据。
// 生成日程表的主函数
int** generateSchedule(int k) {
int n = 1 << k; // 计算n=2^k
// 动态分配二维数组(索引从1开始)
//动态分配行指针数组 :
schedule是指向指针的指针,分配n+1个元素(索引 0~n,实际用 1~n,方便球队 / 天数编号从 1 开始)。int** schedule = (int**)malloc((n + 1) * sizeof(int*));
//为每一行分配列空间 :遍历每个行指针
schedule[i],分配n+1个int空间(列索引 0~n,实际用 1~n)。for (int i = 0; i <= n; i++) {
schedule[i] = (int*)malloc((n + 1) * sizeof(int));
}
//调用
fill函数,从整个矩阵的左上角(1,1)到右下角(n,n)开始递归填充。fill(schedule, 1, 1, n, n);
return schedule;
}
3、核心递归函数
日程表的递归函数fill:递归地填充日程表的指定子矩阵区域
参数说明:
int **schedule:指向二维数组(日程表)的指针,存储最终的比赛日程。int x1, int y1:子矩阵的左上角坐标(行、列)。int x2, int y2:子矩阵的右下角坐标(行、列)。
void fill(int** schedule, int x1, int y1, int x2, int y2) {
int size = x2 - x1 + 1;//计算当前子矩阵的边长(矩阵的行数 / 列数)
//当子矩阵边长为 1(单个元素)时
if (size == 1) {
schedule[x1][y1] = x1;
return;
}
int half = size / 2; //子矩阵大小
// 1、填充左上角子矩阵
fill(schedule, x1, y1, x1 + half - 1, y1 + half - 1); //调用fill函数,递归填充左上角
// 2、填充右上角子矩阵(左上角 + half)
for (int i = x1; i <= x1 + half - 1; i++) {
for (int j = y1 + half; j <= y2; j++) {
schedule[i][j] = schedule[i][j - half] + half;
}
}
// 3、填充左下角子矩阵(等于右上角)
for (int i = x1 + half; i <= x2; i++) {
for (int j = y1; j <= y1 + half - 1; j++) {
schedule[i][j] = schedule[i - half][j + half];
}
}
// 4、填充右下角子矩阵(等于左上角)
for (int i = x1 + half; i <= x2; i++) {
for (int j = y1 + half; j <= y2; j++) {
schedule[i][j] = schedule[i - half][j - half];
}
}
}
4、主程序流程
int main() {
int k;
scanf("%d", &k);
//处理特殊情况 k=0
if (k == 0) {
printf("1\n");
return 0;
}
int n = 1 << k; //计算 n=2^k
int** schedule = generateSchedule(k);
// 输出日程表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
printf("%d ", schedule[i][j]);
}
printf("\n");
}
// 释放内存
for (int i = 0; i <= n; i++) {
free(schedule[i]);
}
free(schedule);
return 0;
}
四、完整代码
cs
#include <stdio.h> //引入标准输入输出库,用于scanf(读取输入)和printf(输出结果)
#include <stdlib.h> //引入标准库,用于malloc(动态分配内存)和free(释放内存)
void fill(int** schedule, int x1, int y1, int x2, int y2) {
int size = x2 - x1 + 1;
if (size == 1) {
schedule[x1][y1] = x1;
return;
}
int half = size / 2;
// 填充左上角子矩阵
fill(schedule, x1, y1, x1 + half - 1, y1 + half - 1);
// 填充右上角子矩阵(左上角 + half)
for (int i = x1; i <= x1 + half - 1; i++) {
for (int j = y1 + half; j <= y2; j++) {
schedule[i][j] = schedule[i][j - half] + half;
}
}
// 填充左下角子矩阵(等于右上角)
for (int i = x1 + half; i <= x2; i++) {
for (int j = y1; j <= y1 + half - 1; j++) {
schedule[i][j] = schedule[i - half][j + half];
}
}
// 填充右下角子矩阵(等于左上角)
for (int i = x1 + half; i <= x2; i++) {
for (int j = y1 + half; j <= y2; j++) {
schedule[i][j] = schedule[i - half][j - half];
}
}
}
// 生成日程表的主函数
int** generateSchedule(int k) {
int n = 1 << k; // 计算n=2^k
// 动态分配二维数组(索引从1开始)
int** schedule = (int**)malloc((n + 1) * sizeof(int*));
for (int i = 0; i <= n; i++) {
schedule[i] = (int*)malloc((n + 1) * sizeof(int));
}
fill(schedule, 1, 1, n, n);
return schedule;
}
int main() {
int k;
scanf("%d", &k);
if (k == 0) {
printf("1\n");
return 0;
}
int n = 1 << k;
int** schedule = generateSchedule(k);
// 输出日程表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
printf("%d ", schedule[i][j]);
}
printf("\n");
}
// 释放内存
for (int i = 0; i <= n; i++) {
free(schedule[i]);
}
free(schedule);
return 0;
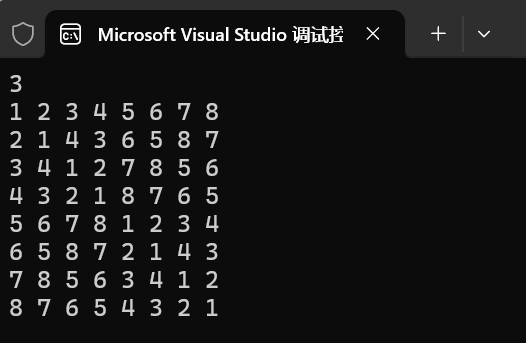
}五、运行结果