Week 1
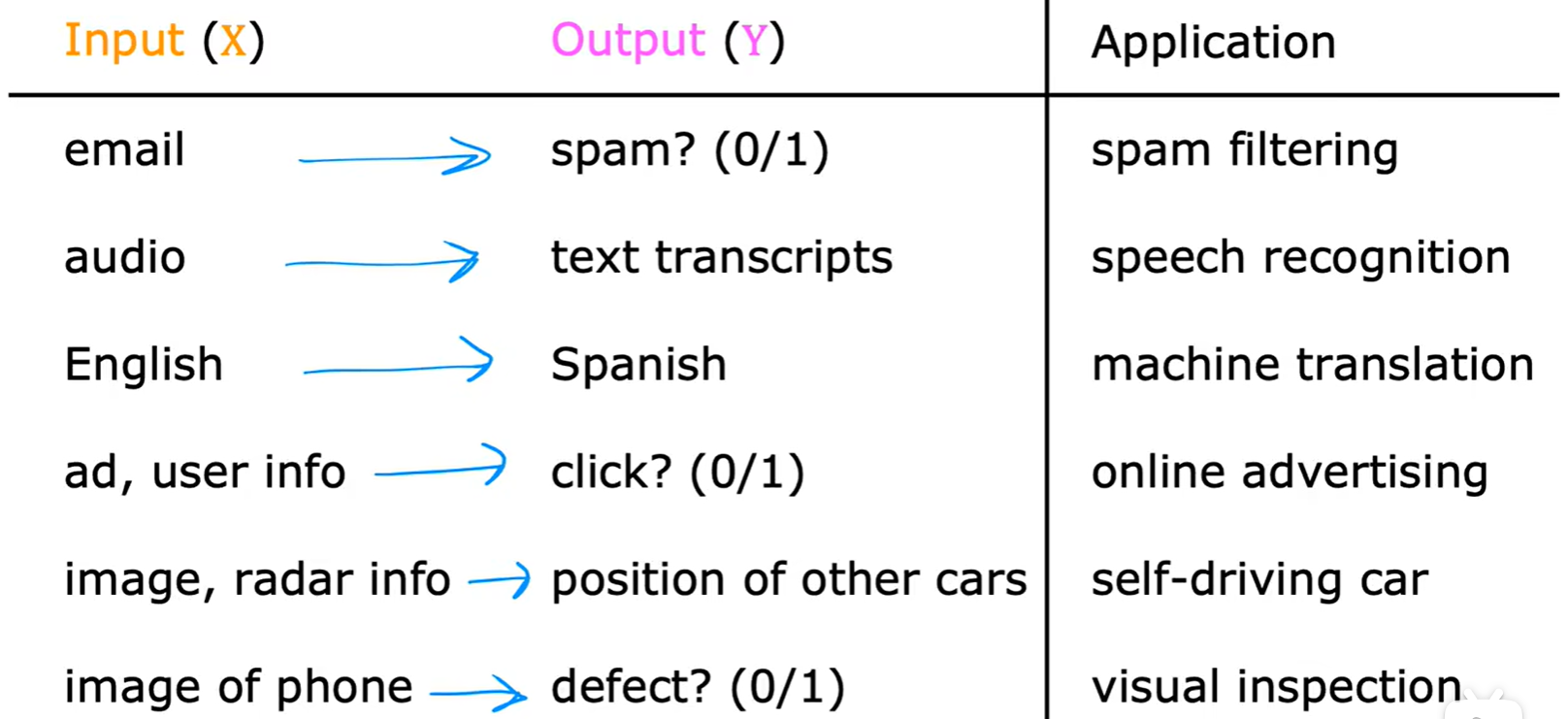
1.1 Supervised learning
- 监督学习
- 本质:学习输入、输出,或 x -> y 的映射;
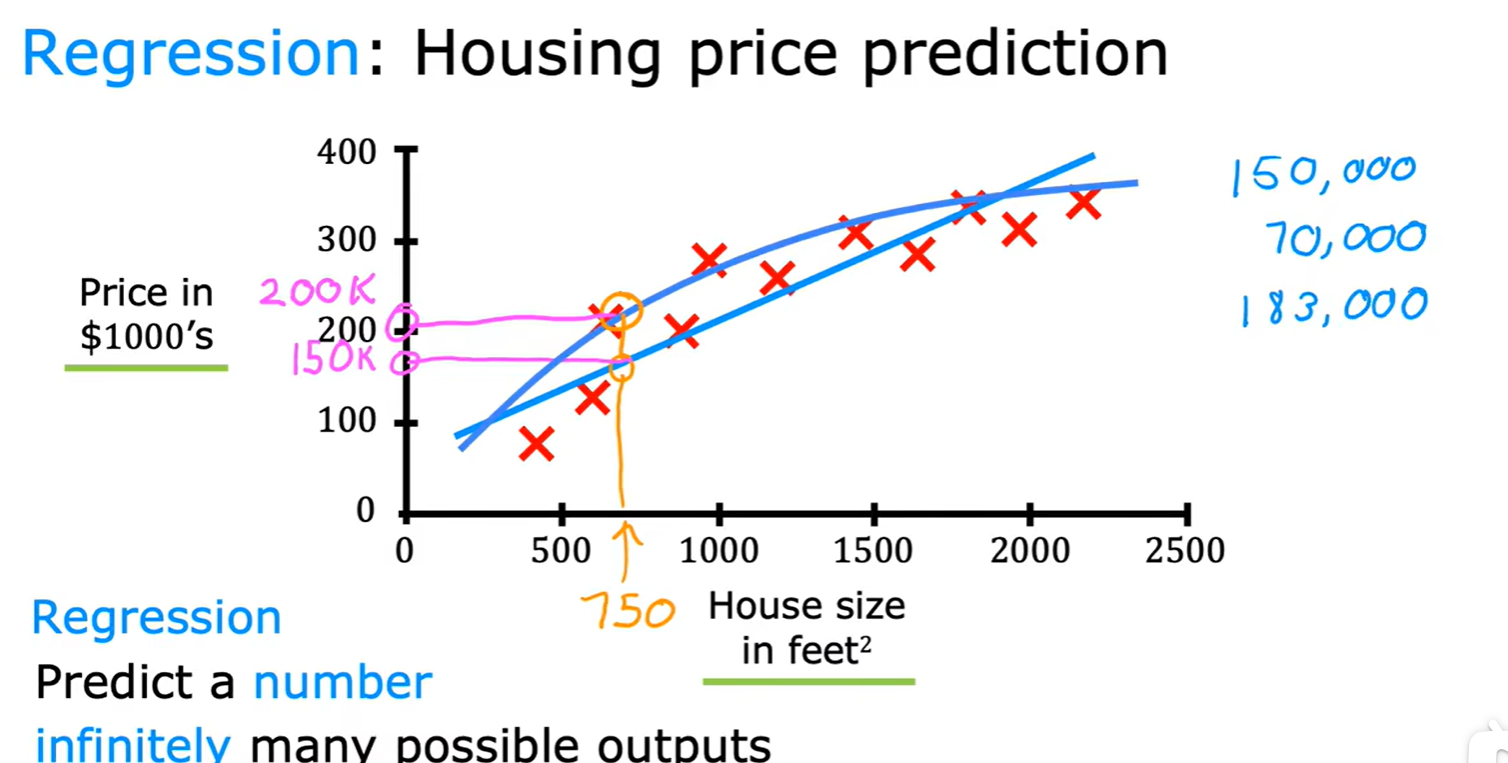
Regression
- 回归算法:房价预测;
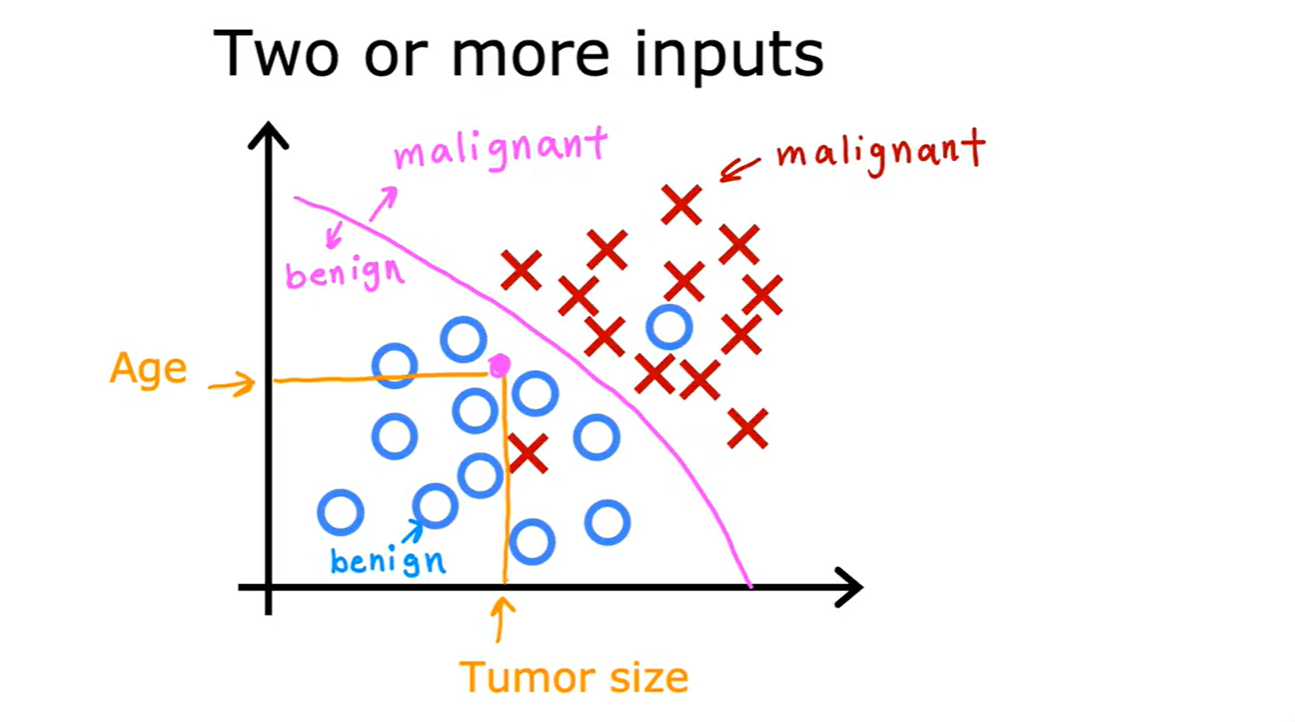
Classification
- 分类算法:肿瘤预测;
1.2 Unsupervised learning
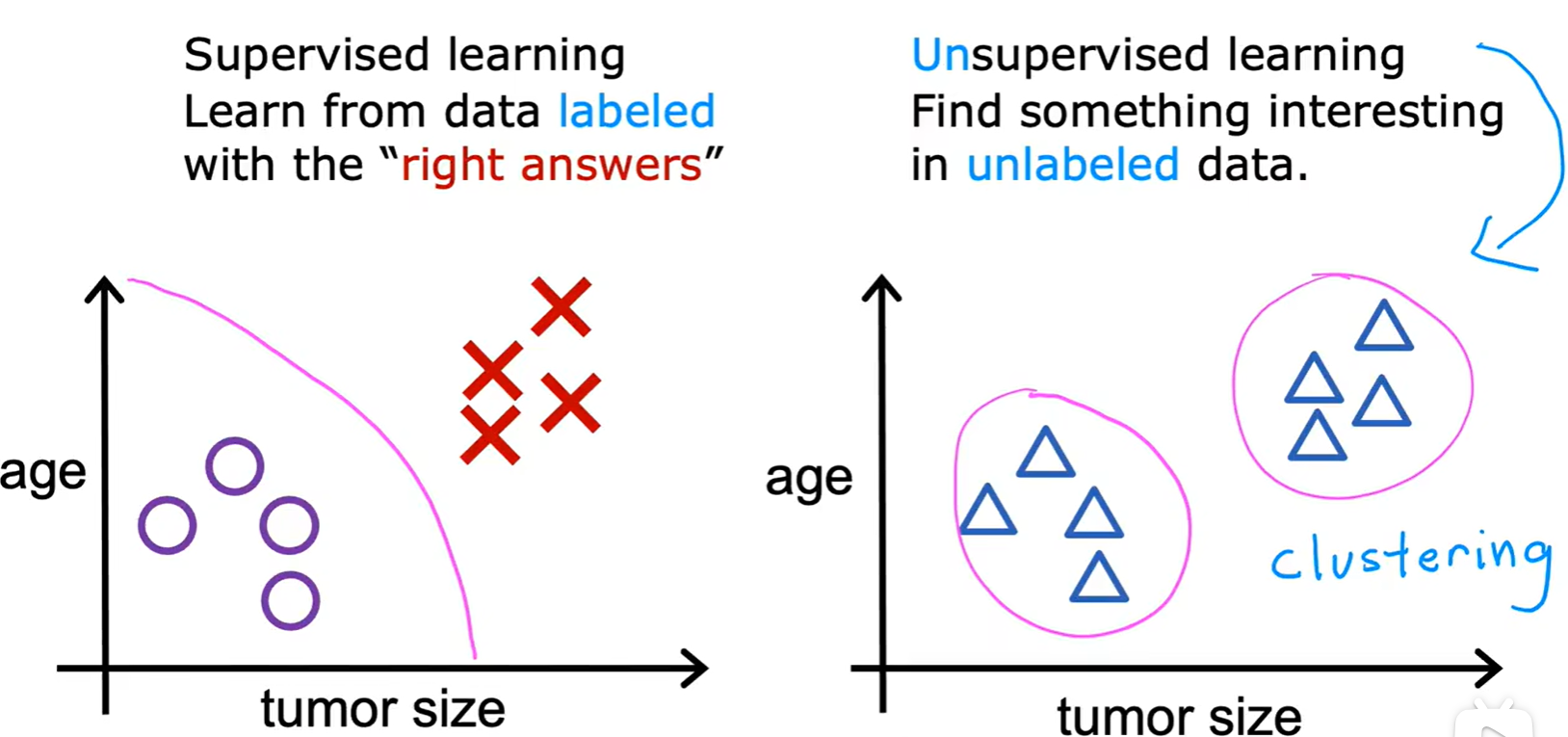
Clustering
- 无监督学习
- 本质:从输入数据中发现潜在的结构或模式,而不是根据已知的答案进行预测;
- 聚类:谷歌新闻,DNA序列,人群分组;
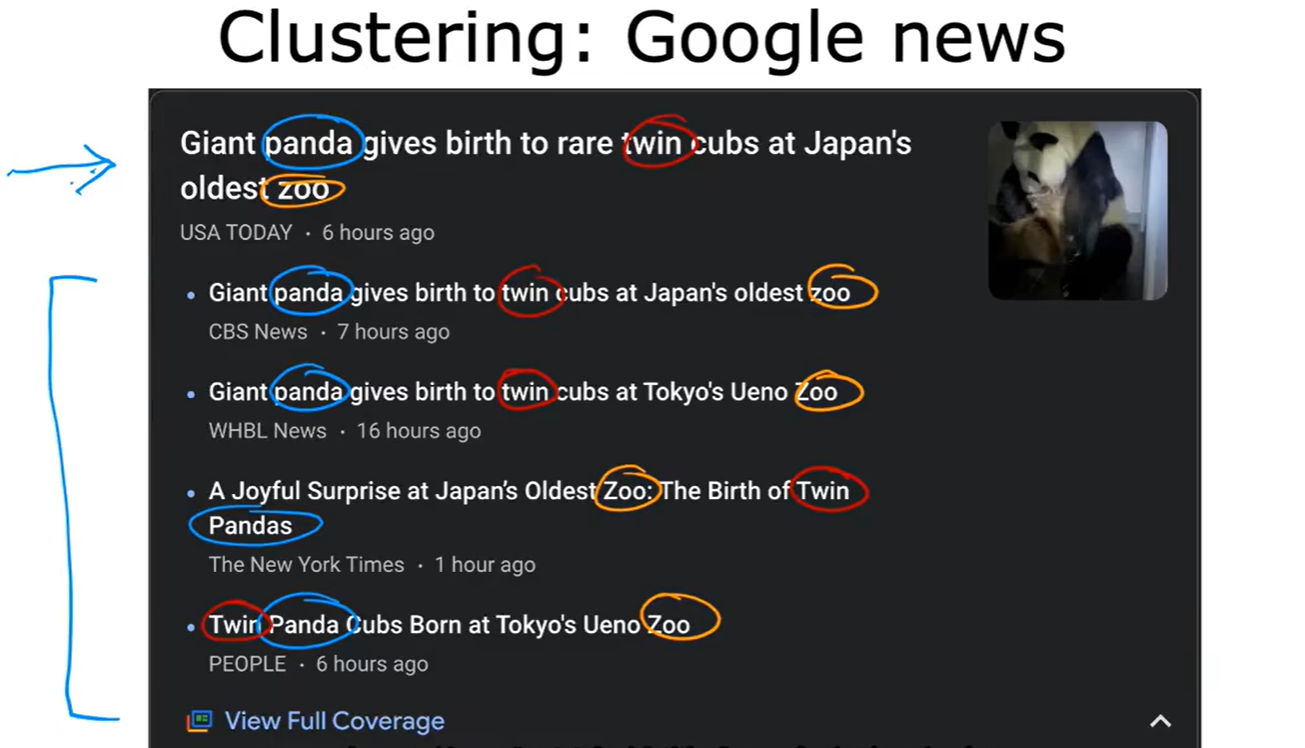

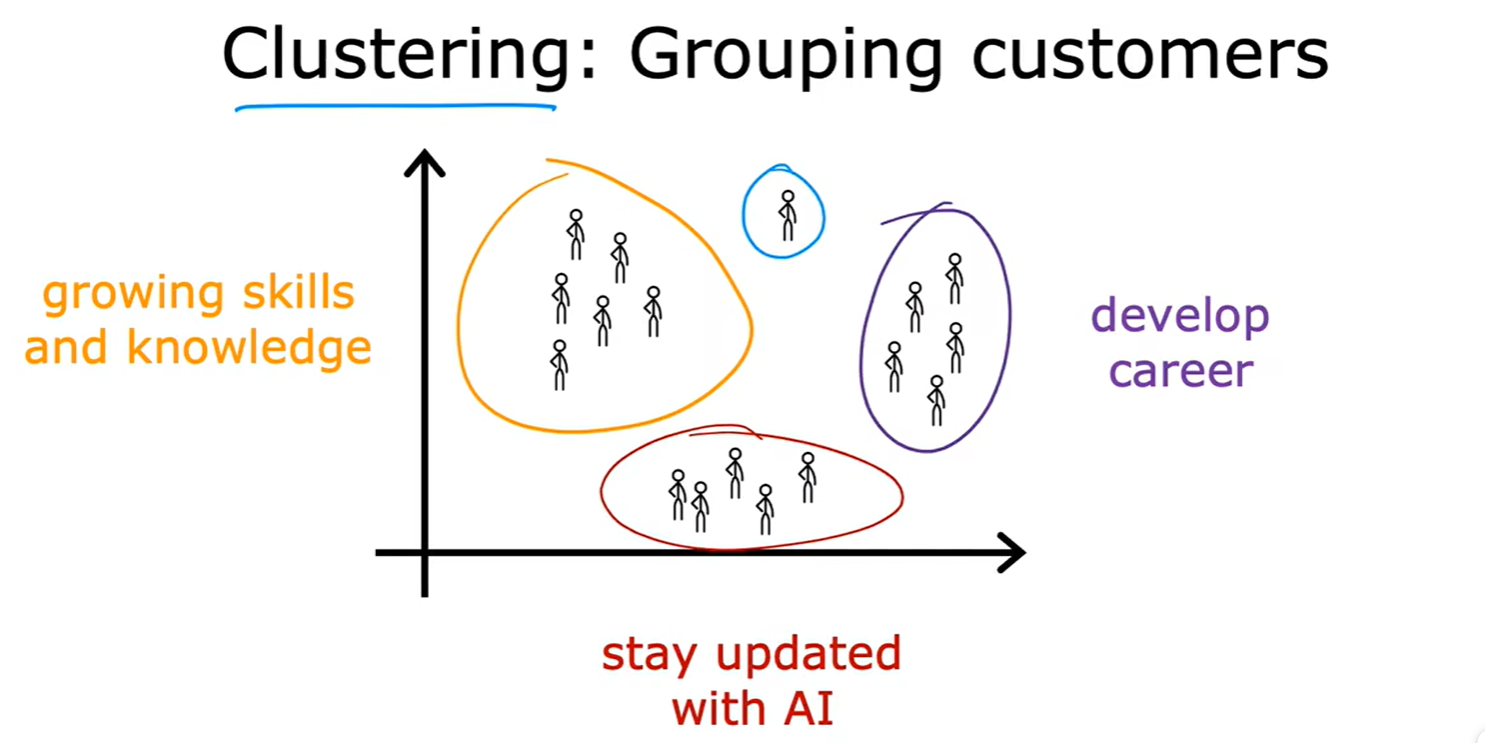
Anomaly Detection
- 异常检测(Anomaly Detection):识别数据中不符合预期模式的异常点,常用于网络安全、欺诈检测等领域。
Dimensionality Reduction
- 降维(Dimensionality Reduction):通过减少数据中的特征数量,提取出最重要的信息。
1.3 Linear Regression
House size and price
- 回归预测的结果有无数个,而分类的结果有限;
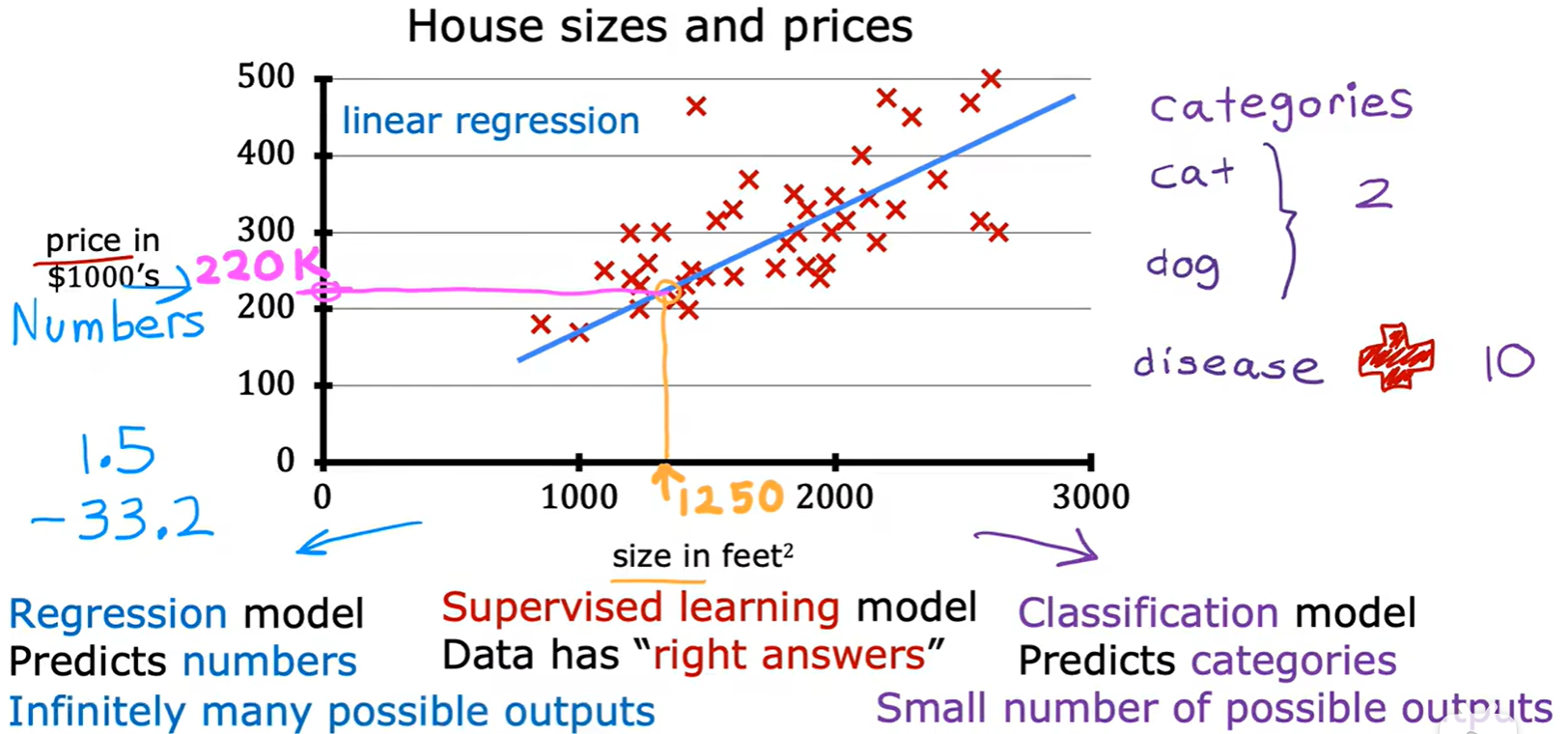
- 几个术语:
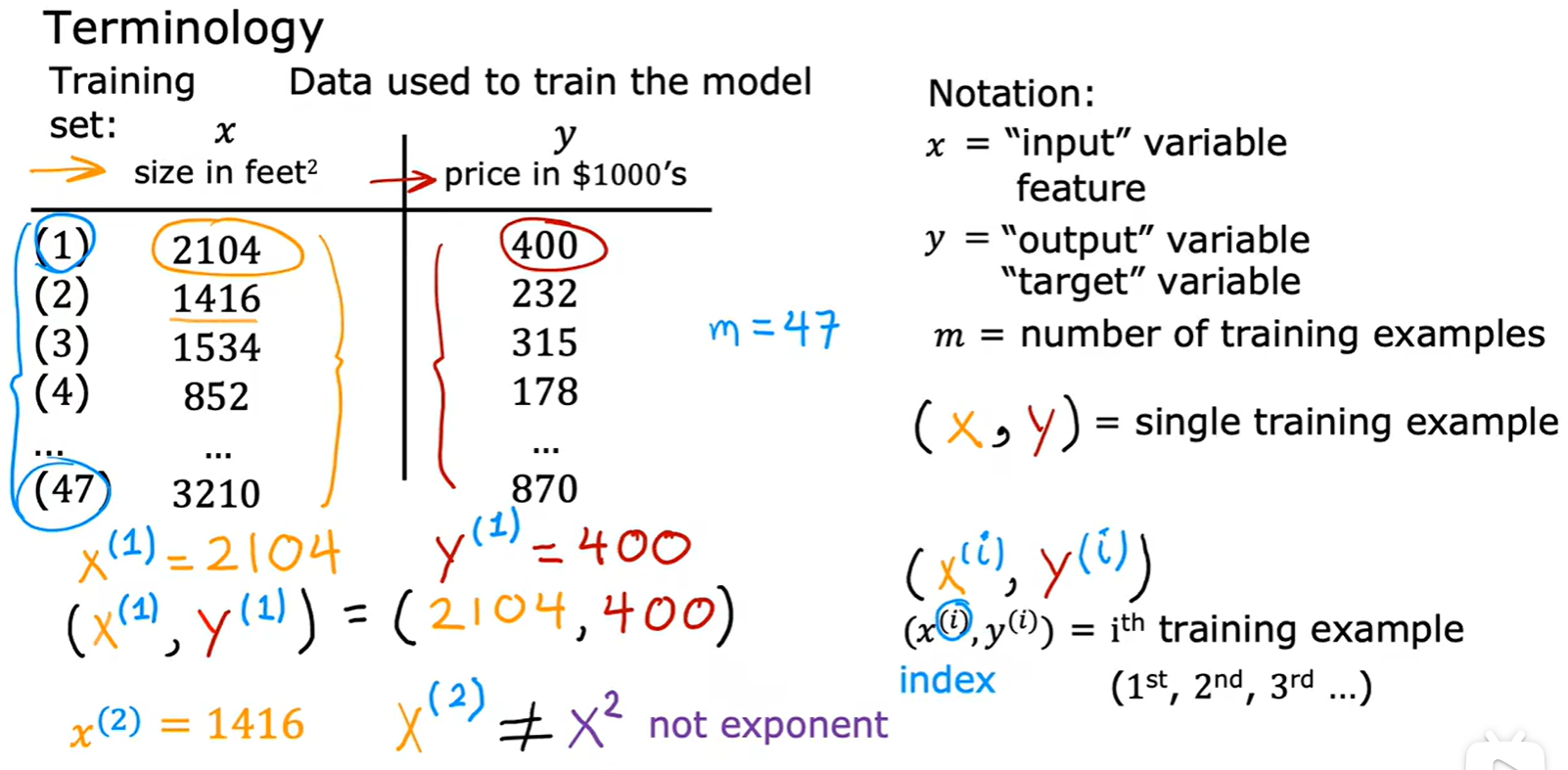
- 构造线性模型:这里为单变量;
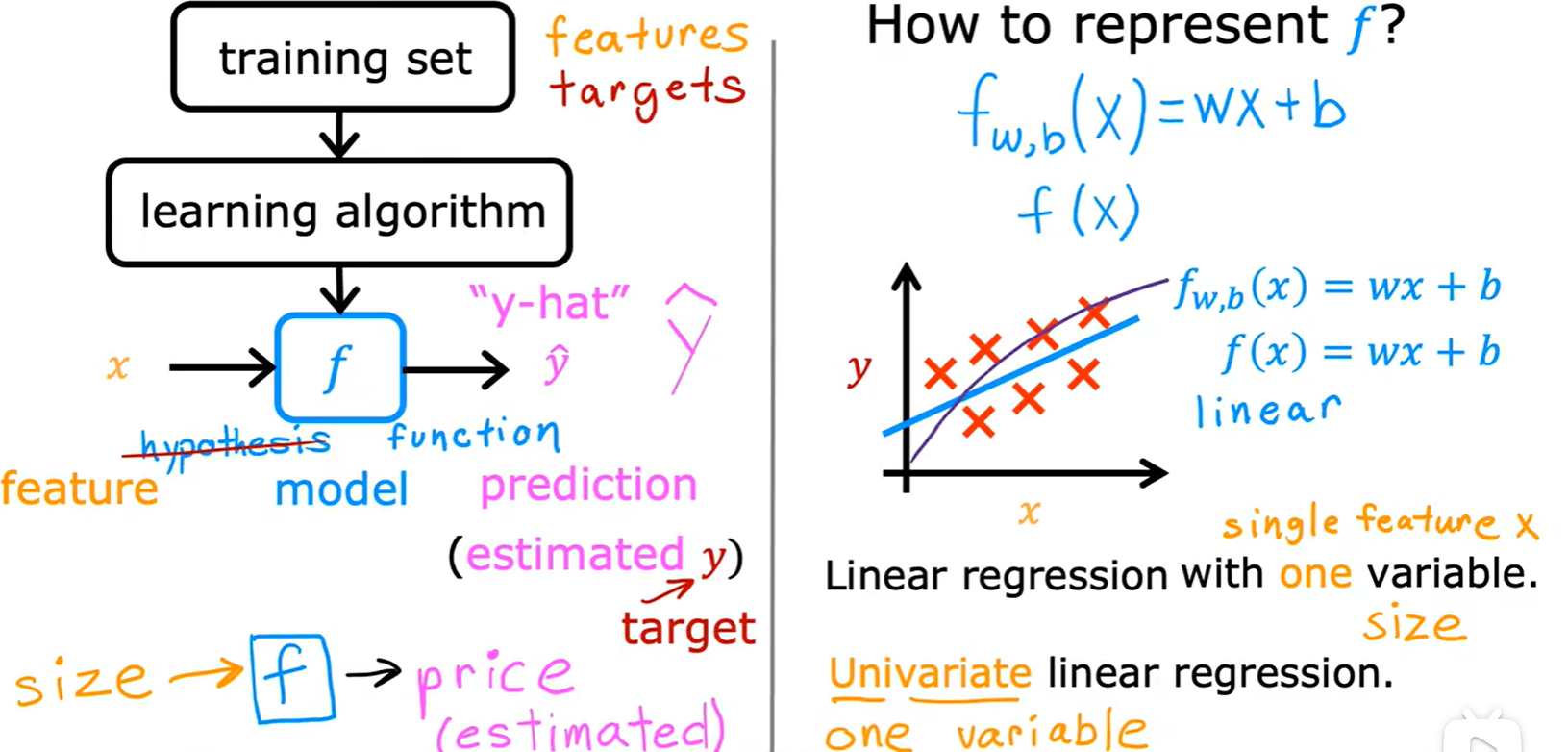
Cost function
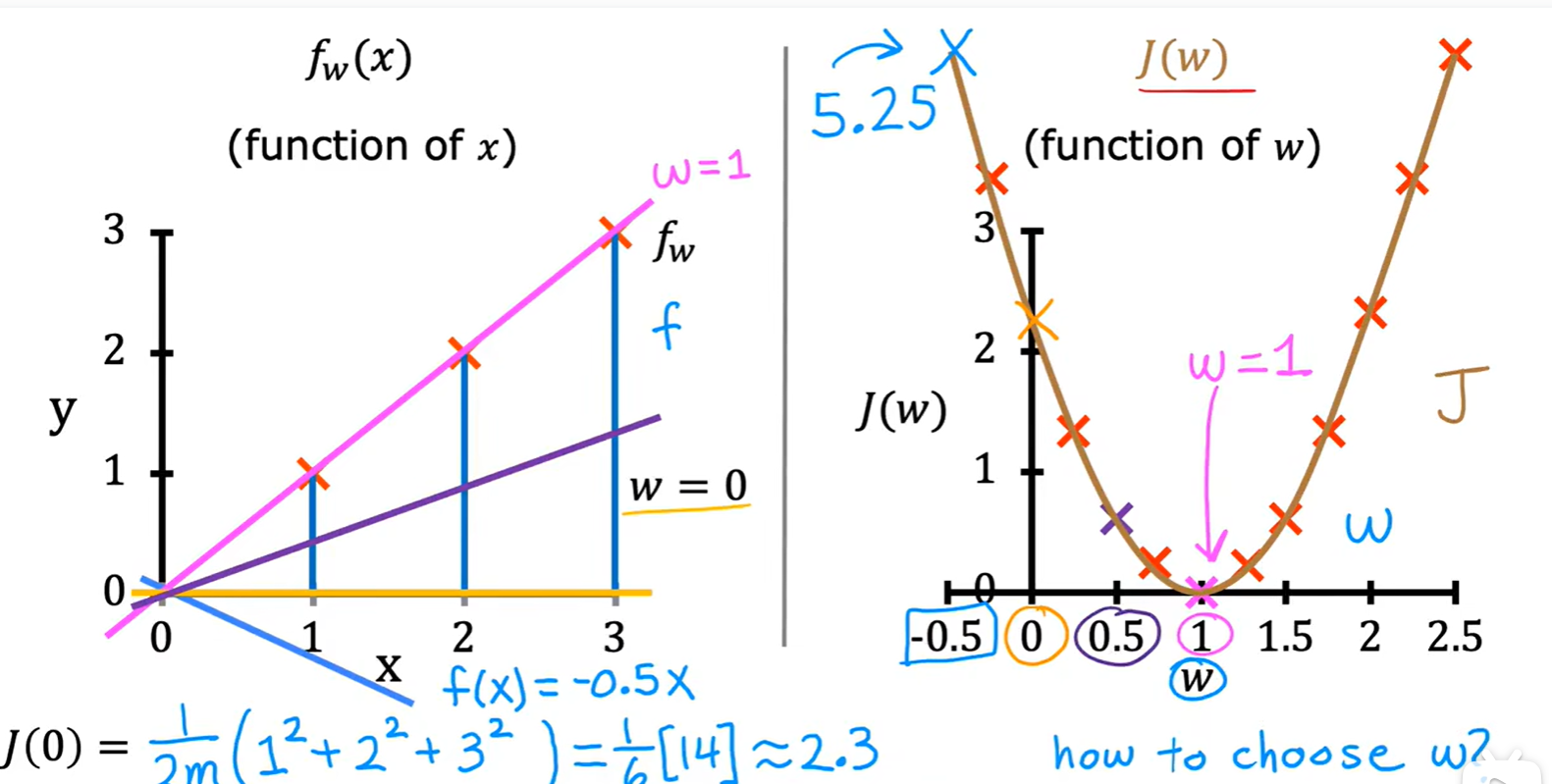
- 这里除以2只是为了求导计算方便;

- 单变量线性模型损失函数:
Gradient descent
- 双变量线性模型损失函数:
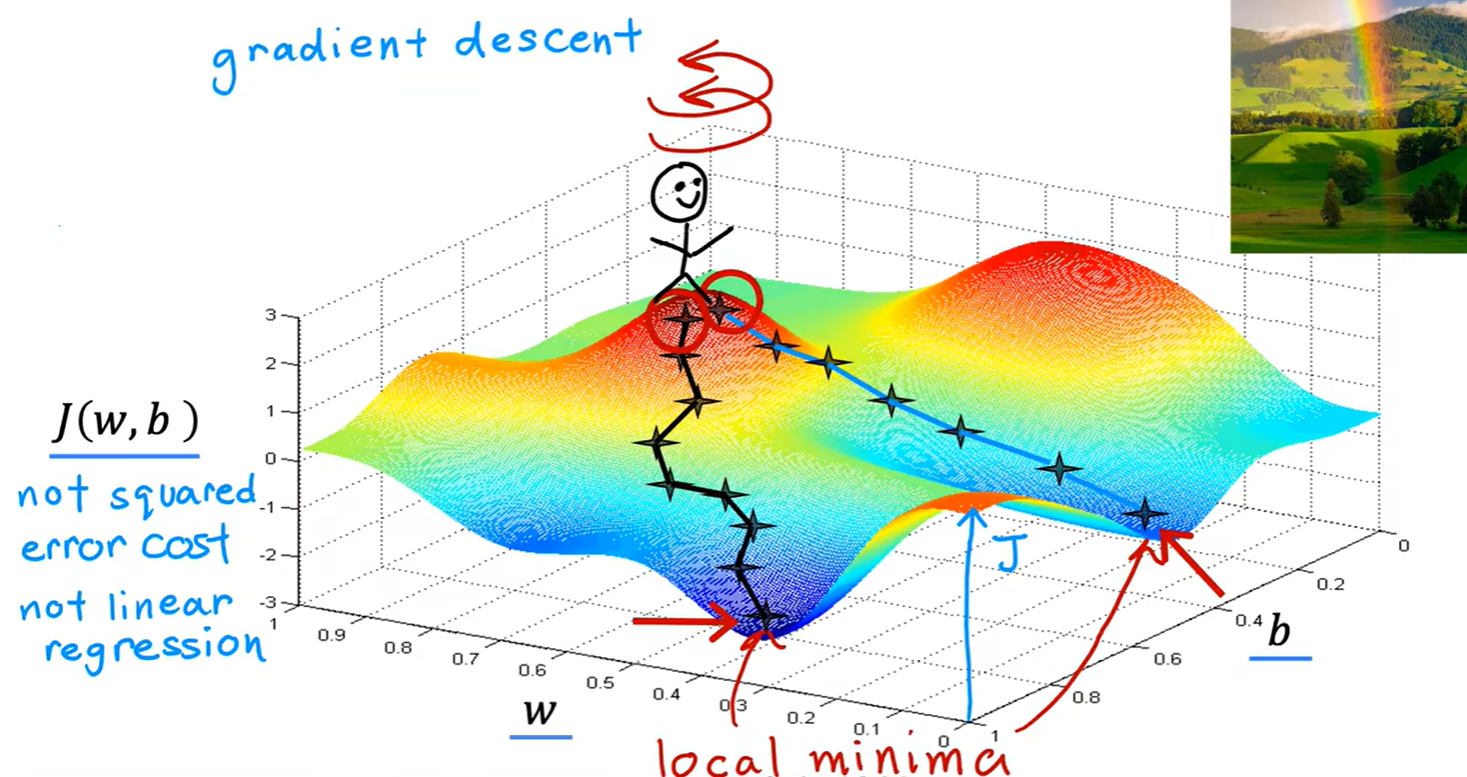
- 参数的更新:

Learning rate
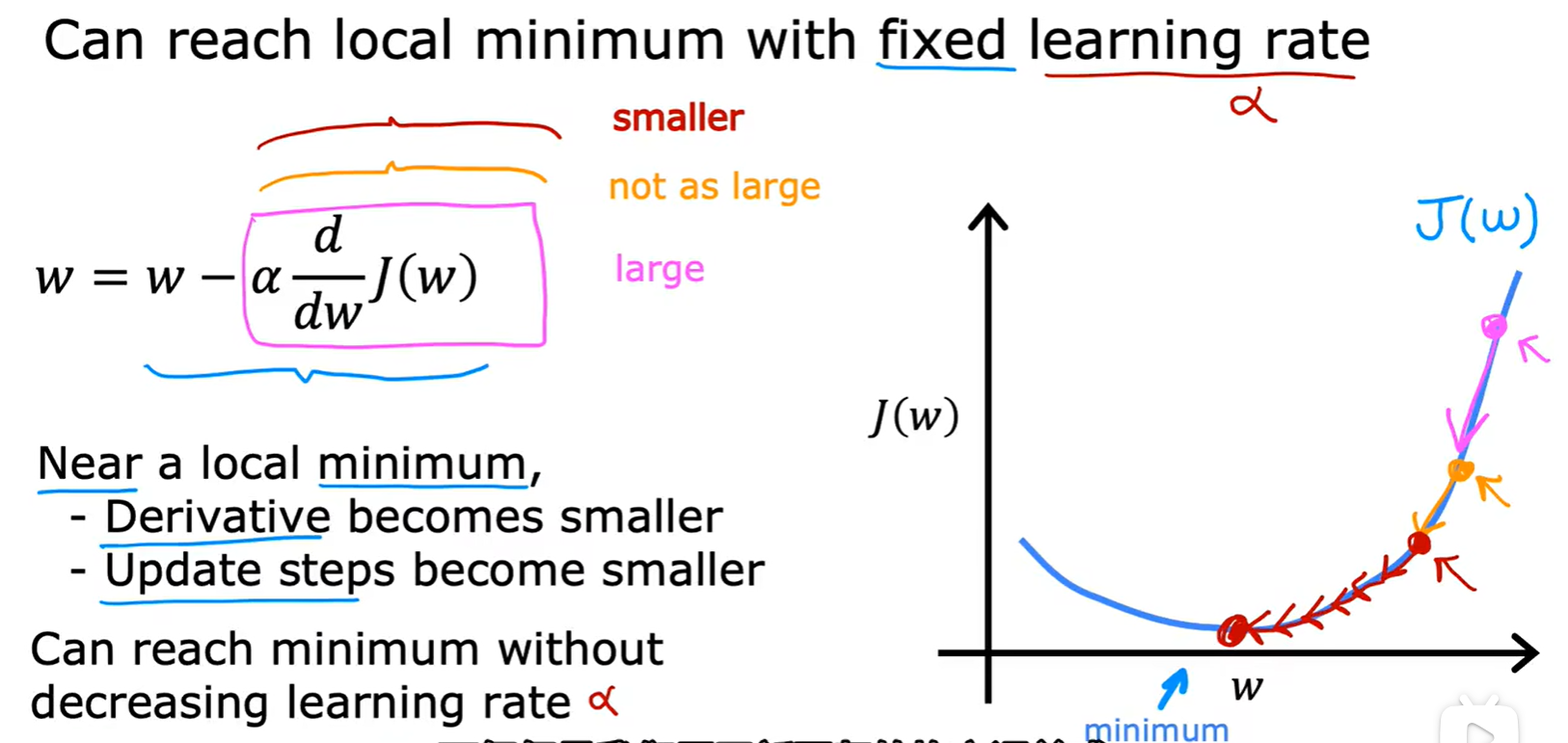
Week 2
2.1 Multiple Linear Regression
- 多元线性回归:多个输入变量影响
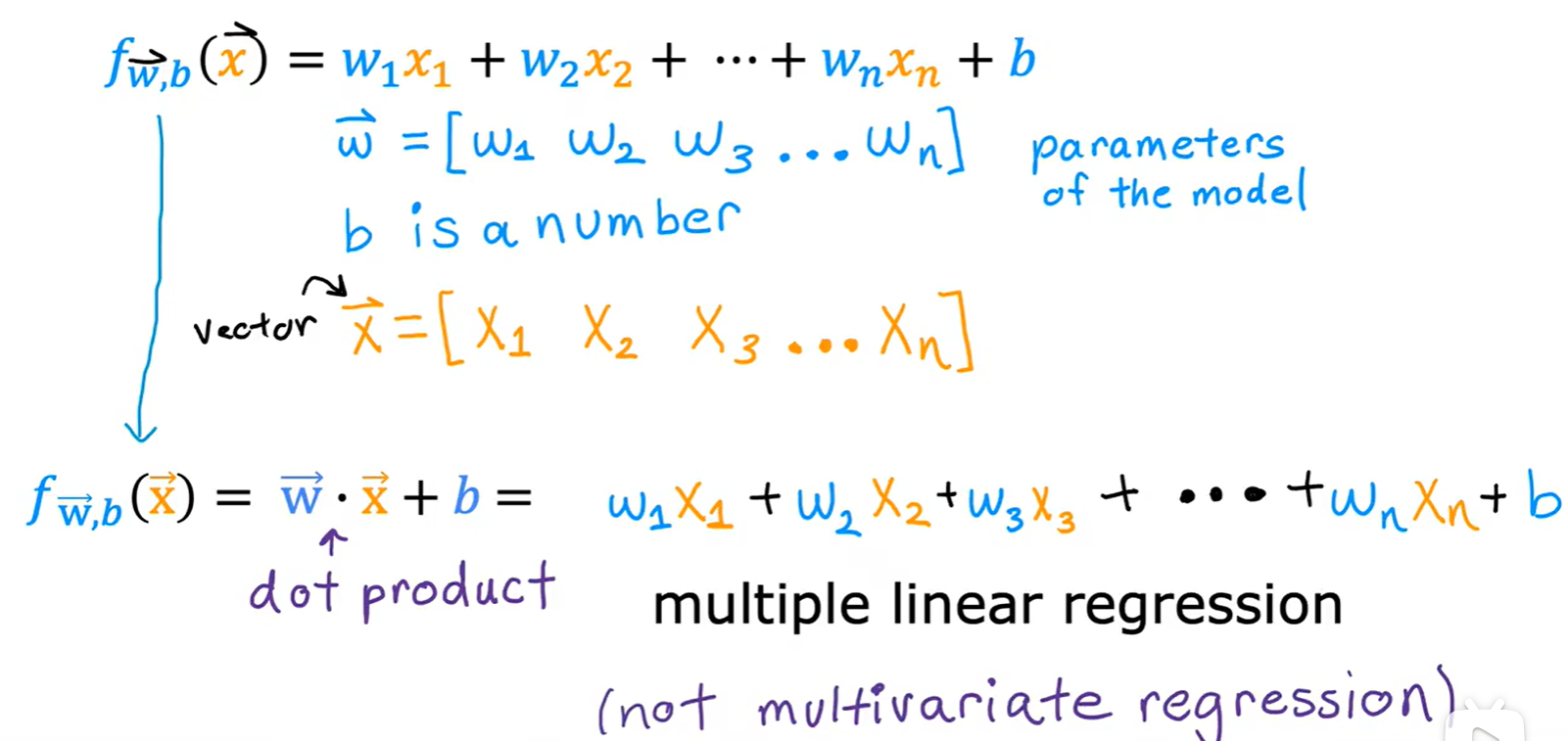
Vectorization
- 向量运算更快的原理:并行计算;

- 多元参数更新:
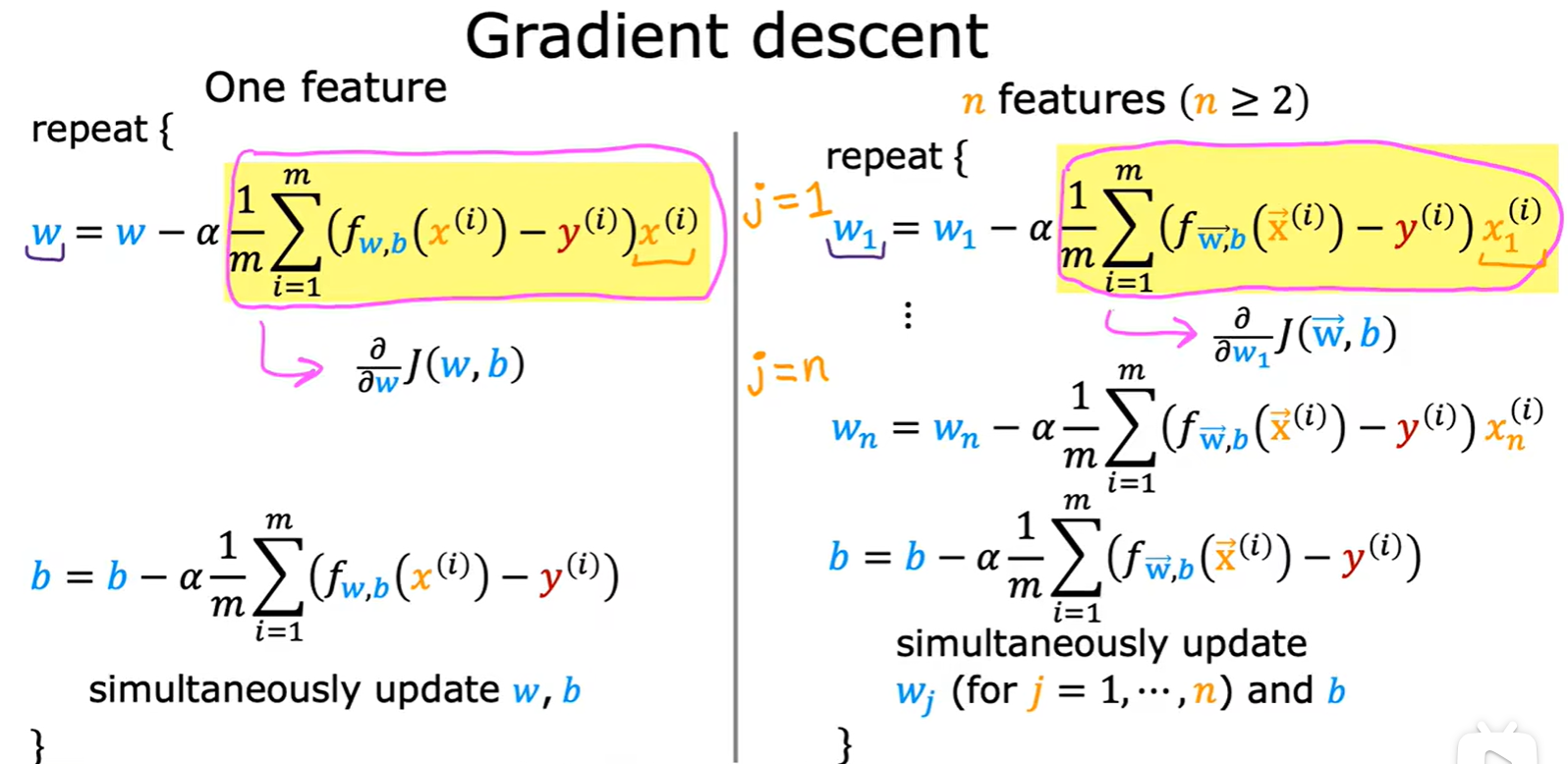
Normal equation
- 正规方程:只运用于线性回归模型,求解损失函数最小值的 w 和 b,无需迭代;
2.2 Featrue scaling
- 特征缩放:使梯度下降运行的更快;
- 方法:将不同特征的取值范围调整到合适大小;
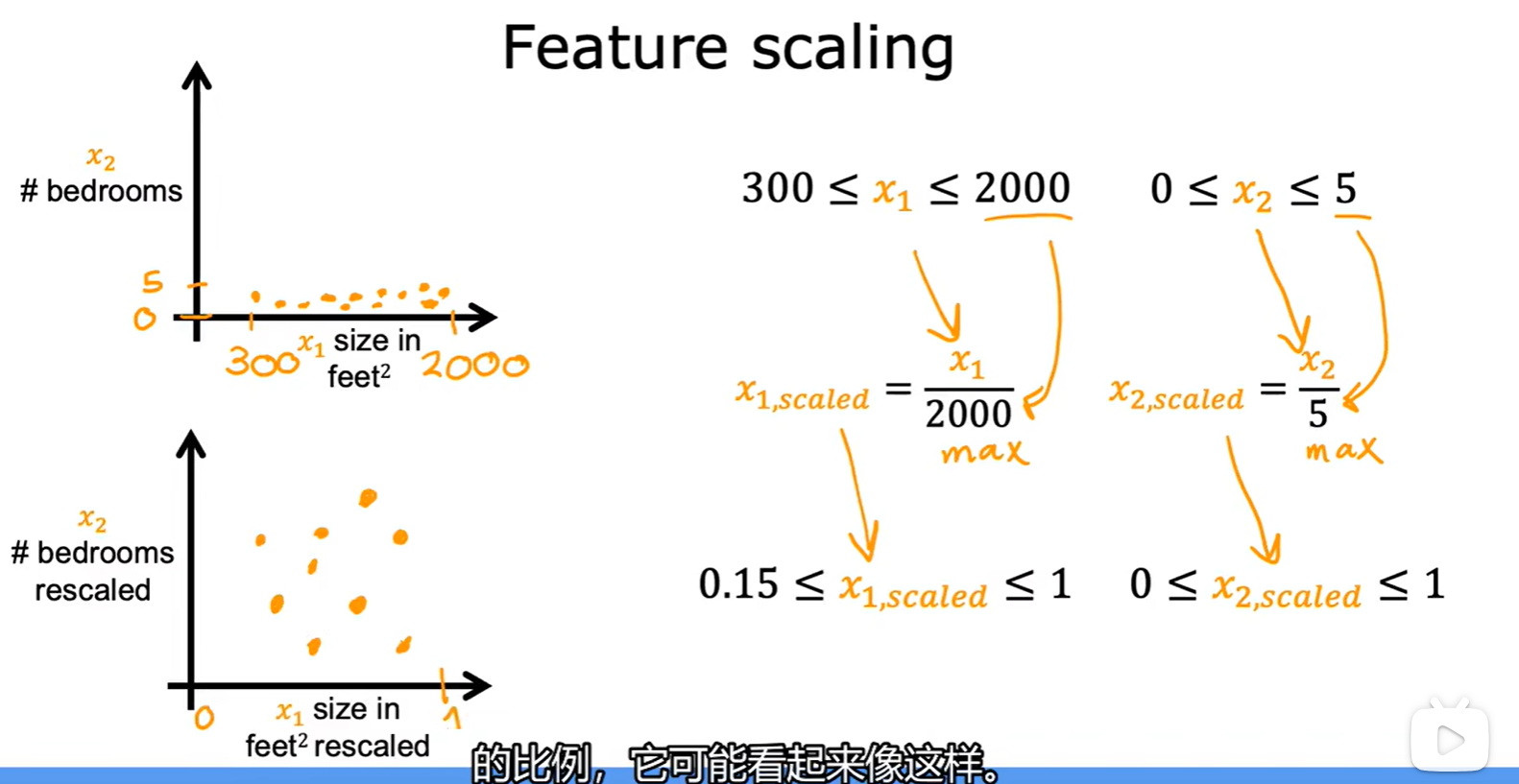
Mean normalization

Z-score normalization
- 就是概率论中的正态分布;
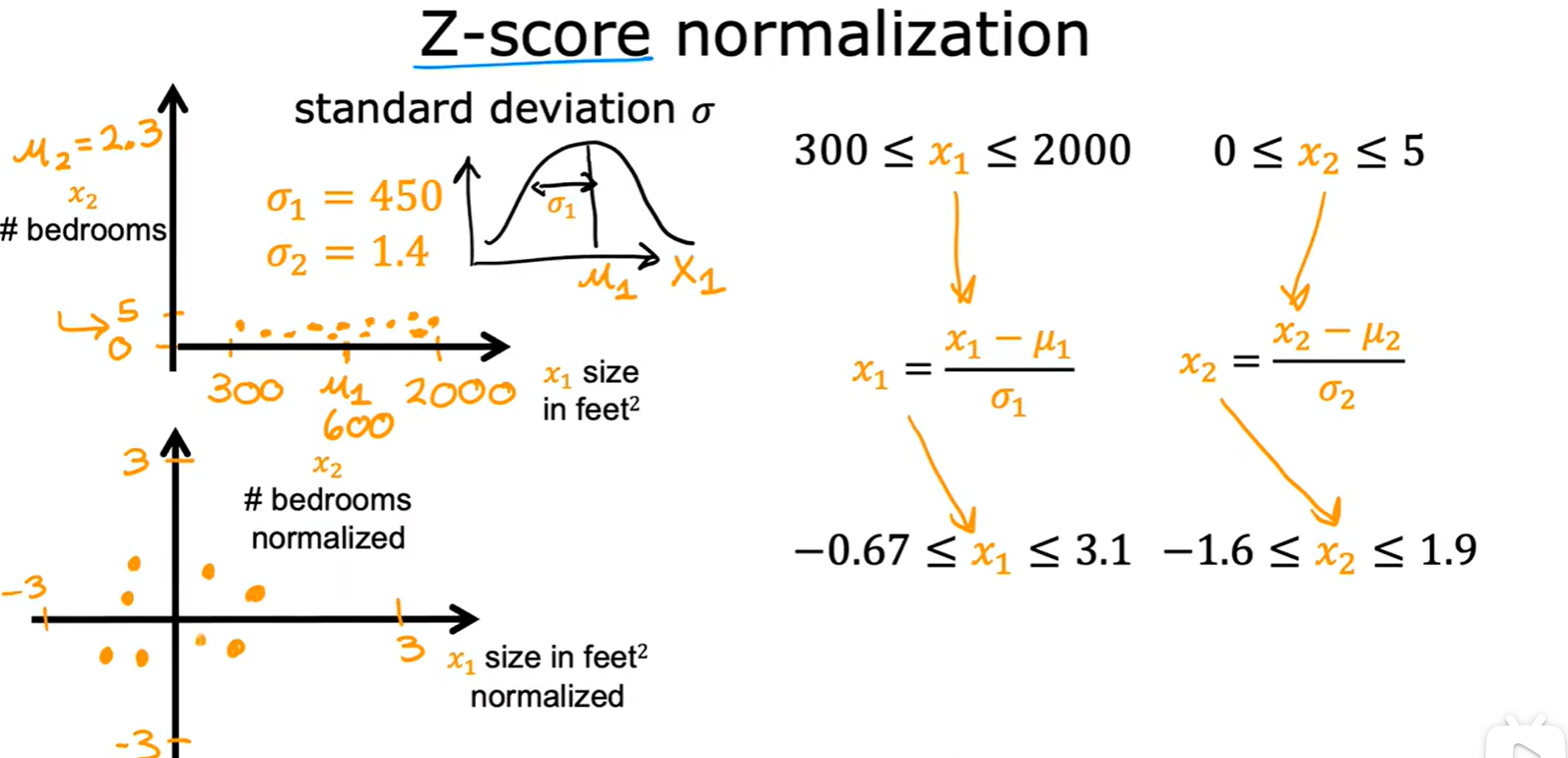
How to choose Alpha
- 学习率太大会产生波动,太小会导致迭代次数增加;
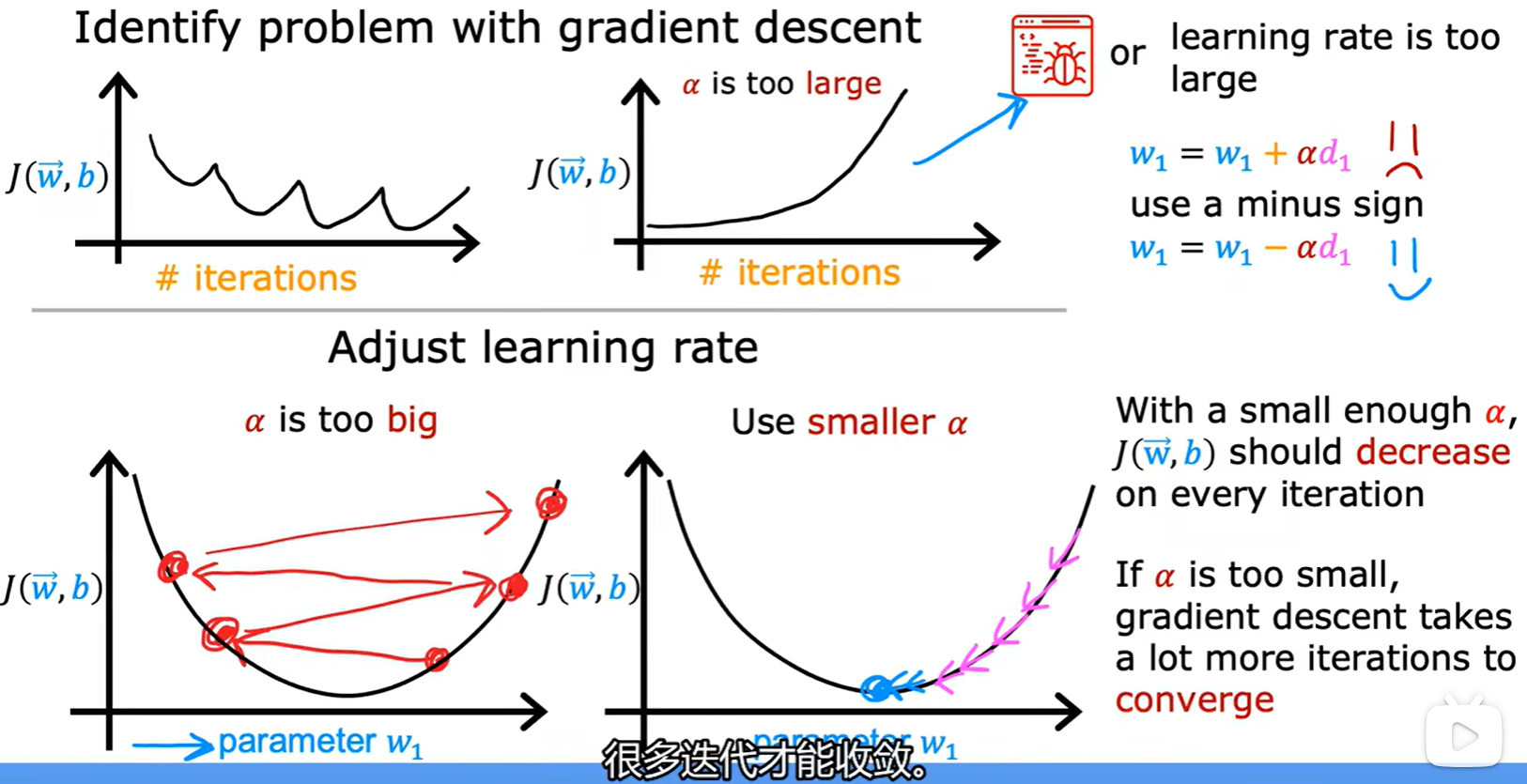
- 怎么调节学习率:
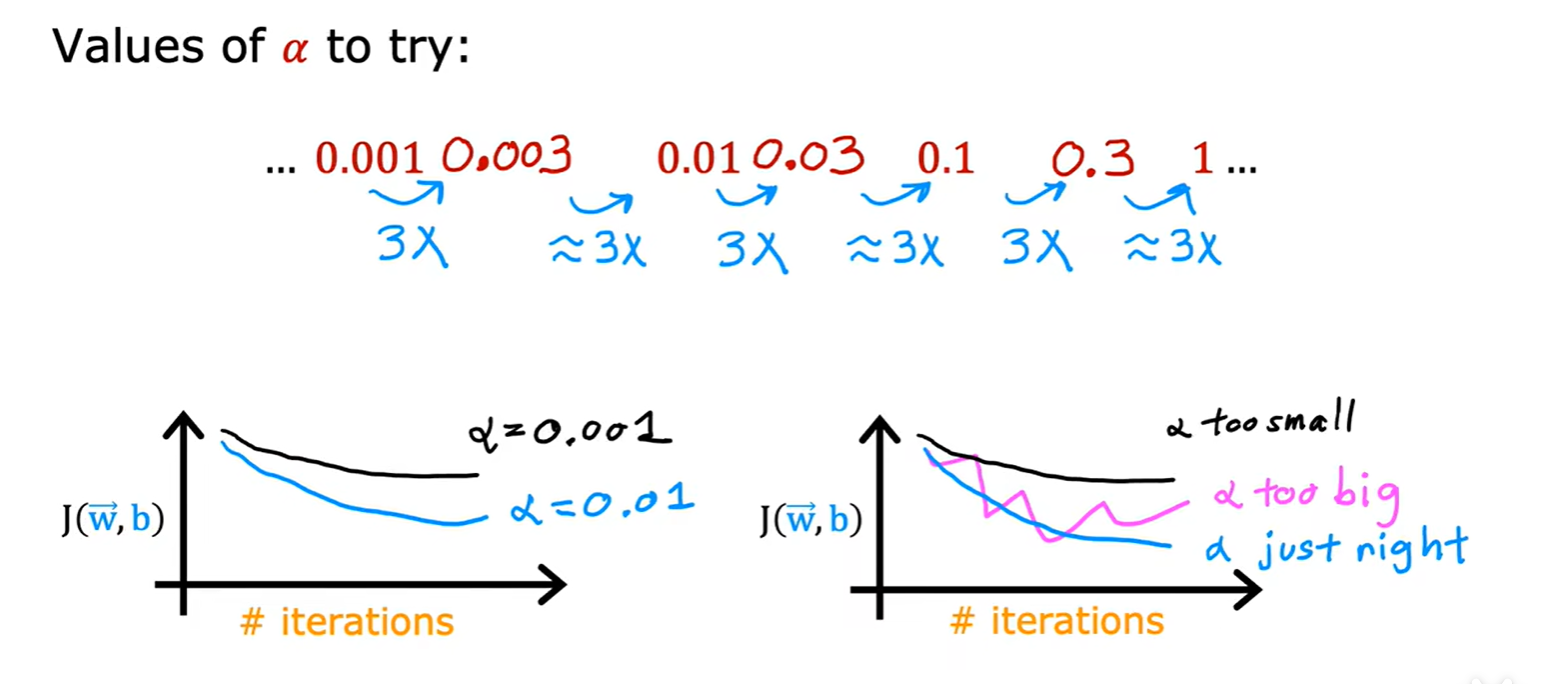
2.3 Featrue Engineering
How to choose featrue
- 通过选择原始特征去组合出新的特征进行拟合:
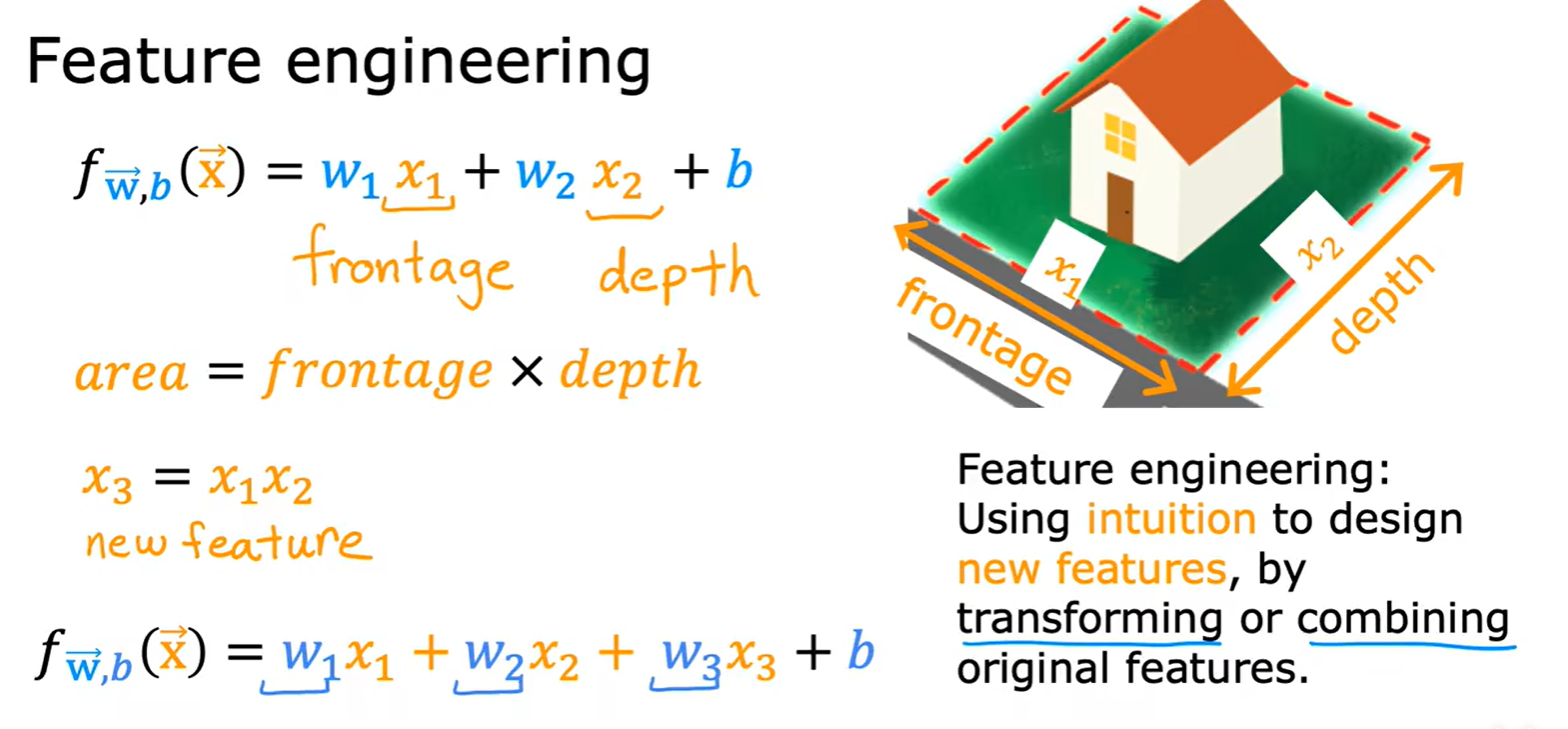
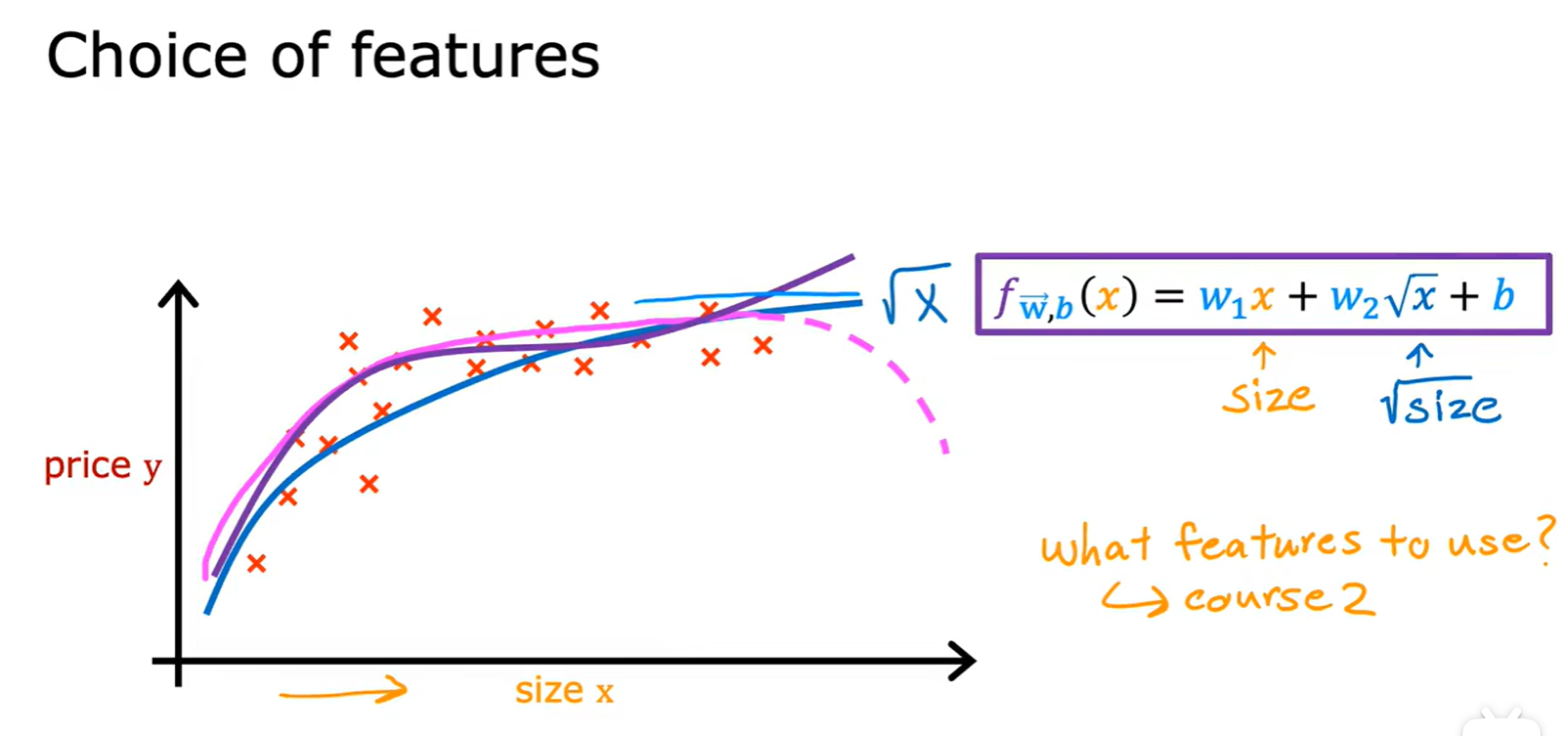
Polynomial Regression
- 多项式回归:通过使用特征工程和多项式函数,得到更好的模型;
Week 3
3.1 Logistic Regression
Sigmoid function

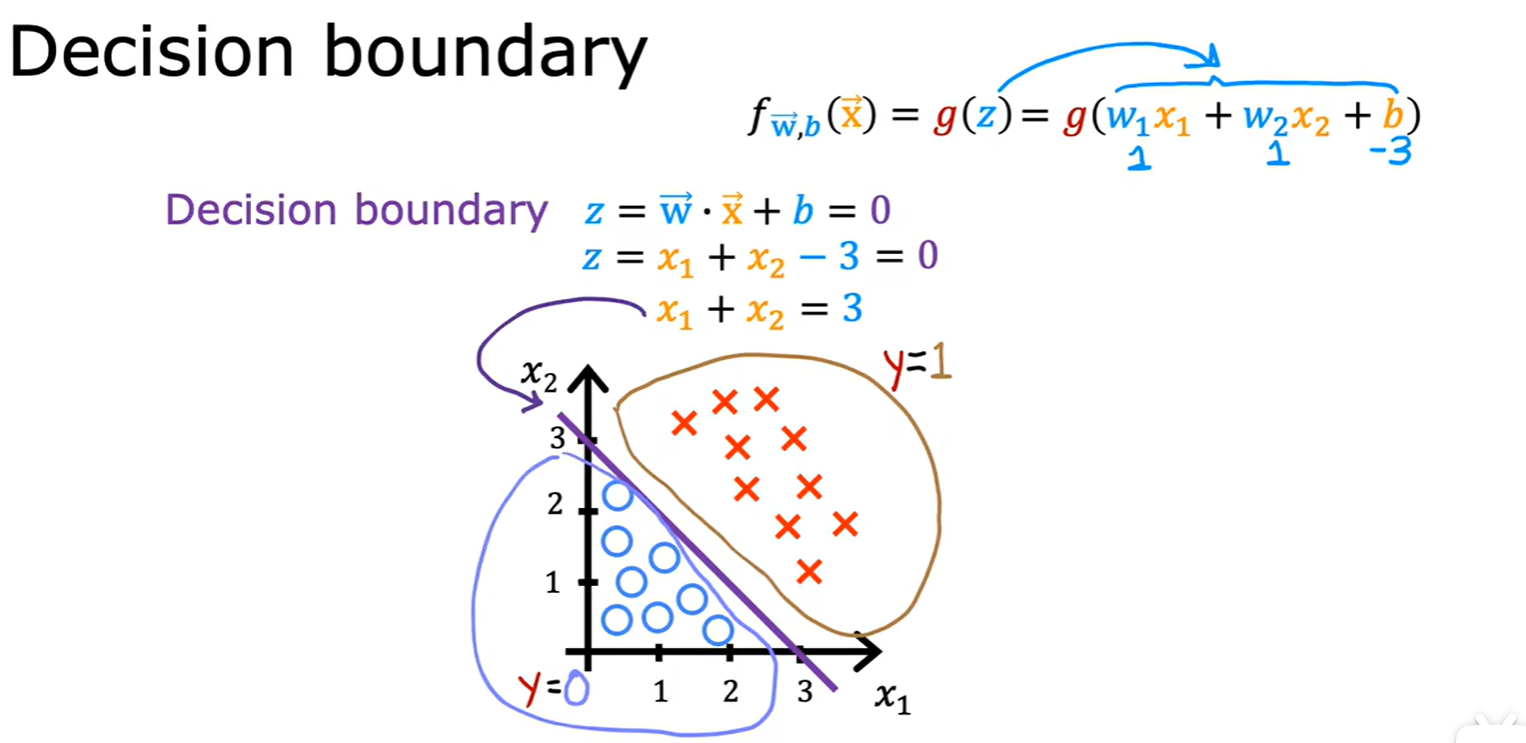
Decision Boundary
- 决策边界:可以是线性,也可以是非线性;

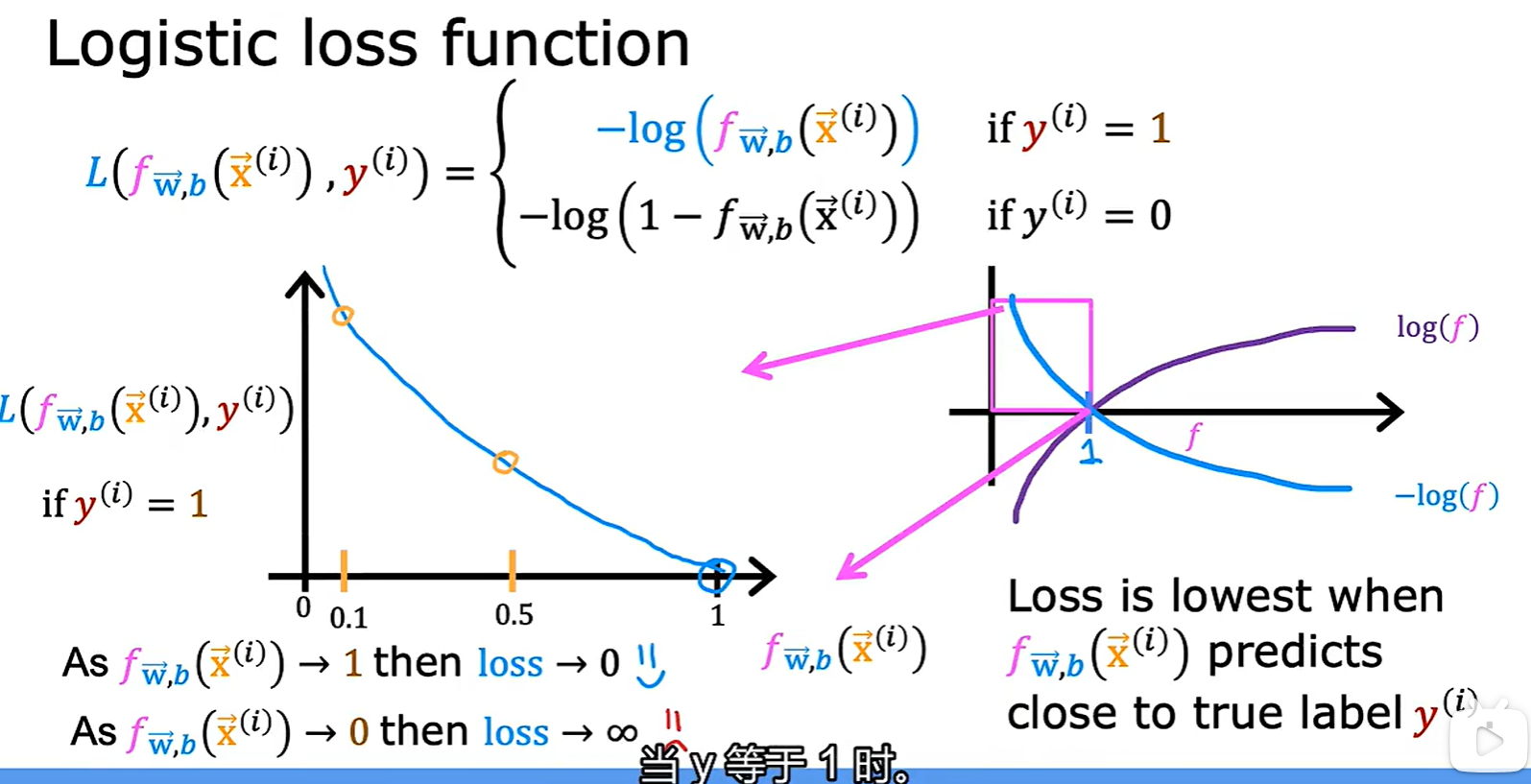
Logistic loss function
- 经过 logistic 转化后的结果处于 0 - 1 之间,在这个区间内 log 函数单调,且取值为 0 - ∞;
- 简化的损失函数:是一个凸函数

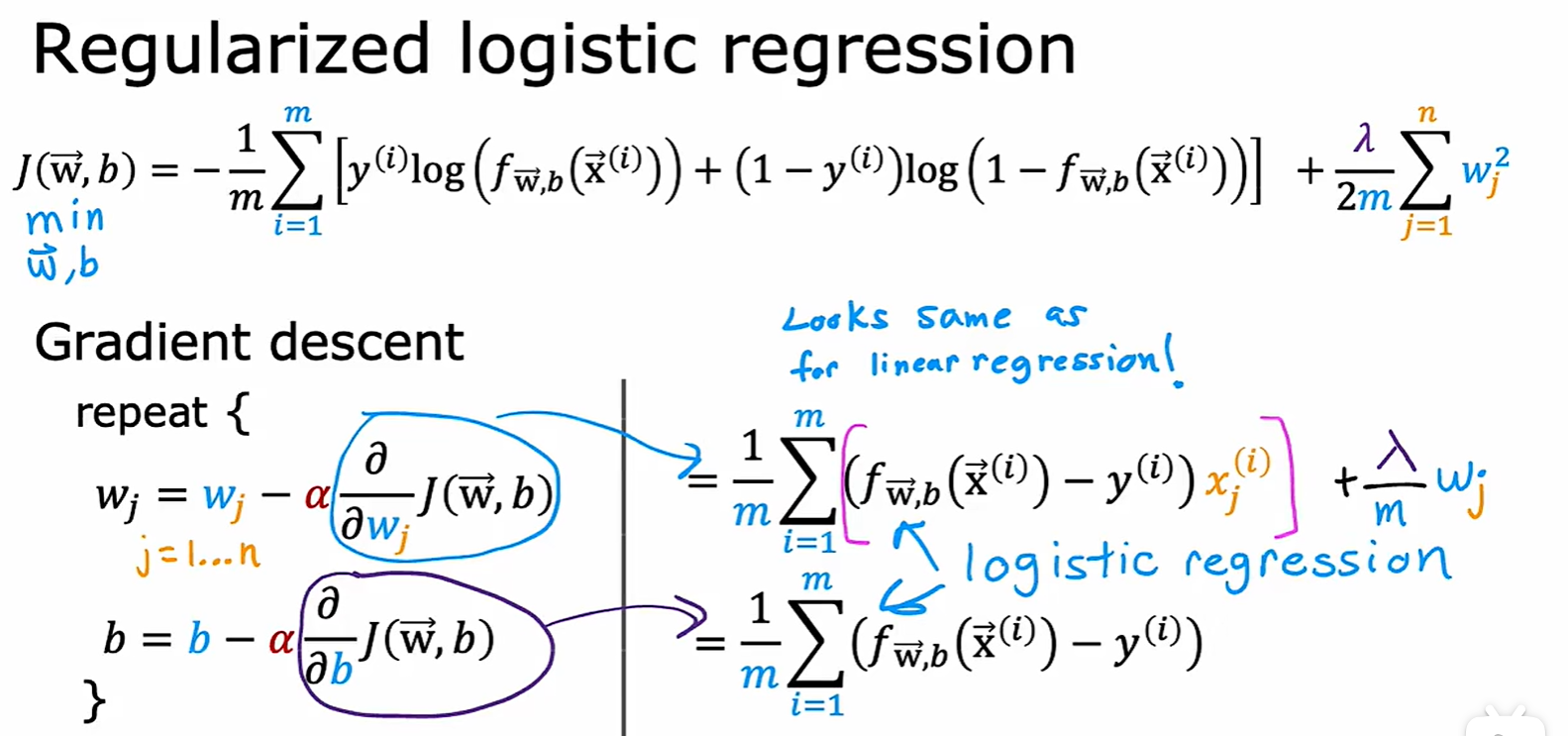
Gradient descent
- 和线性回归中梯度下降的不同点,就是 y_pred 不一样了,增加了 logistic 变换;

3.2 Underfitting and Overfitting
- 欠拟合和过拟合:线性模型和分类模型中均有出现;

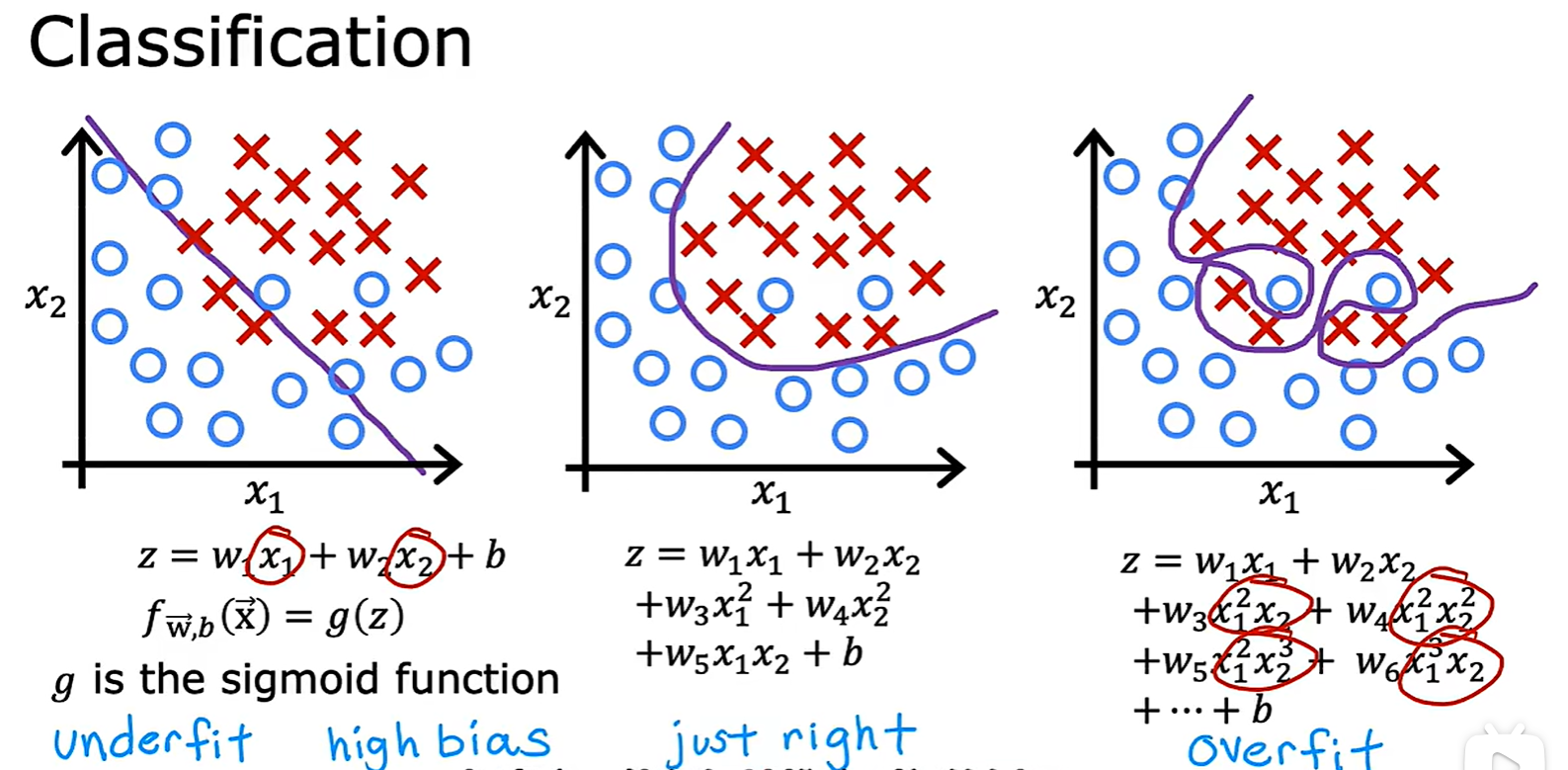
Address Overfitting
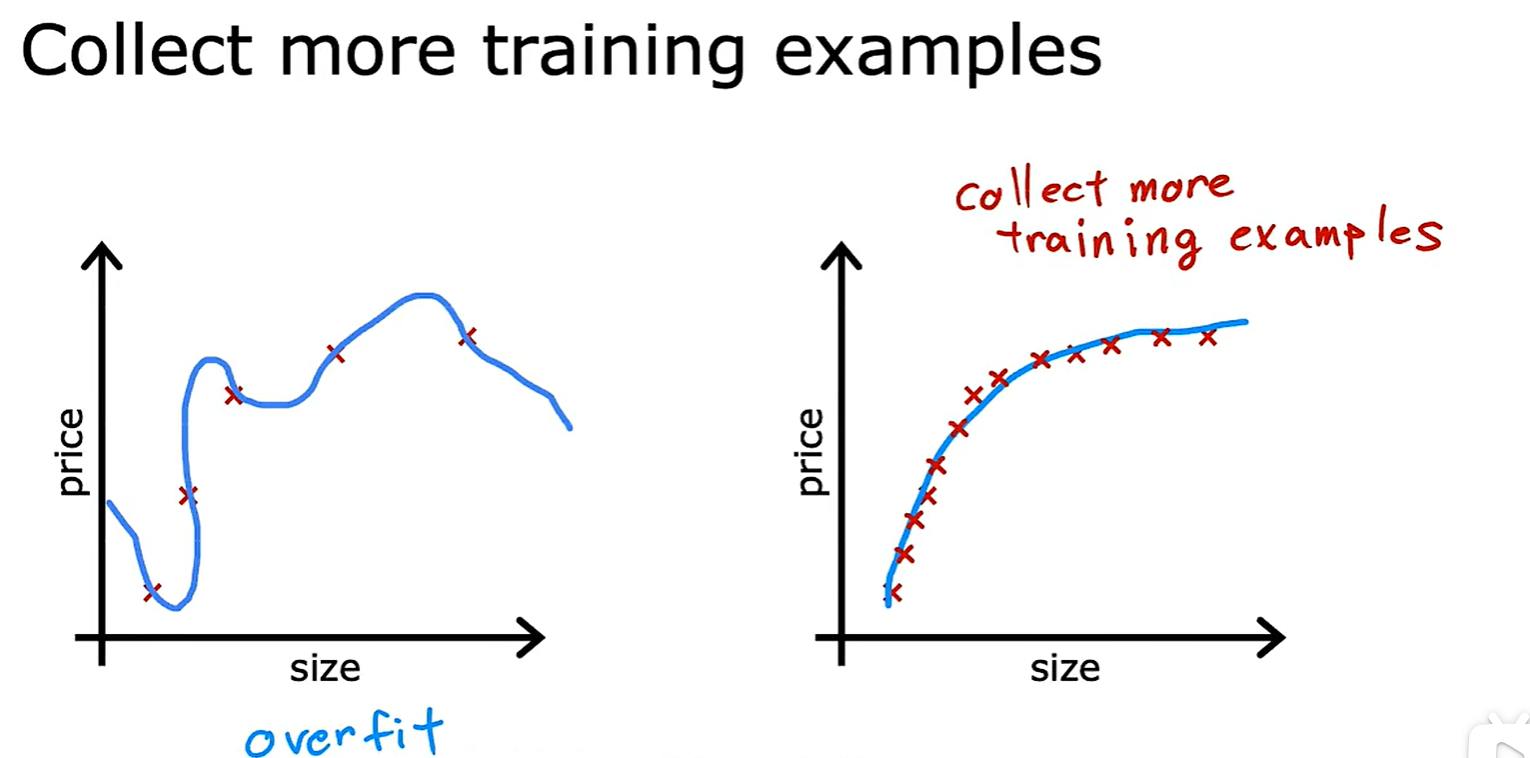
- 法一:Collect more data,收集更多的数据
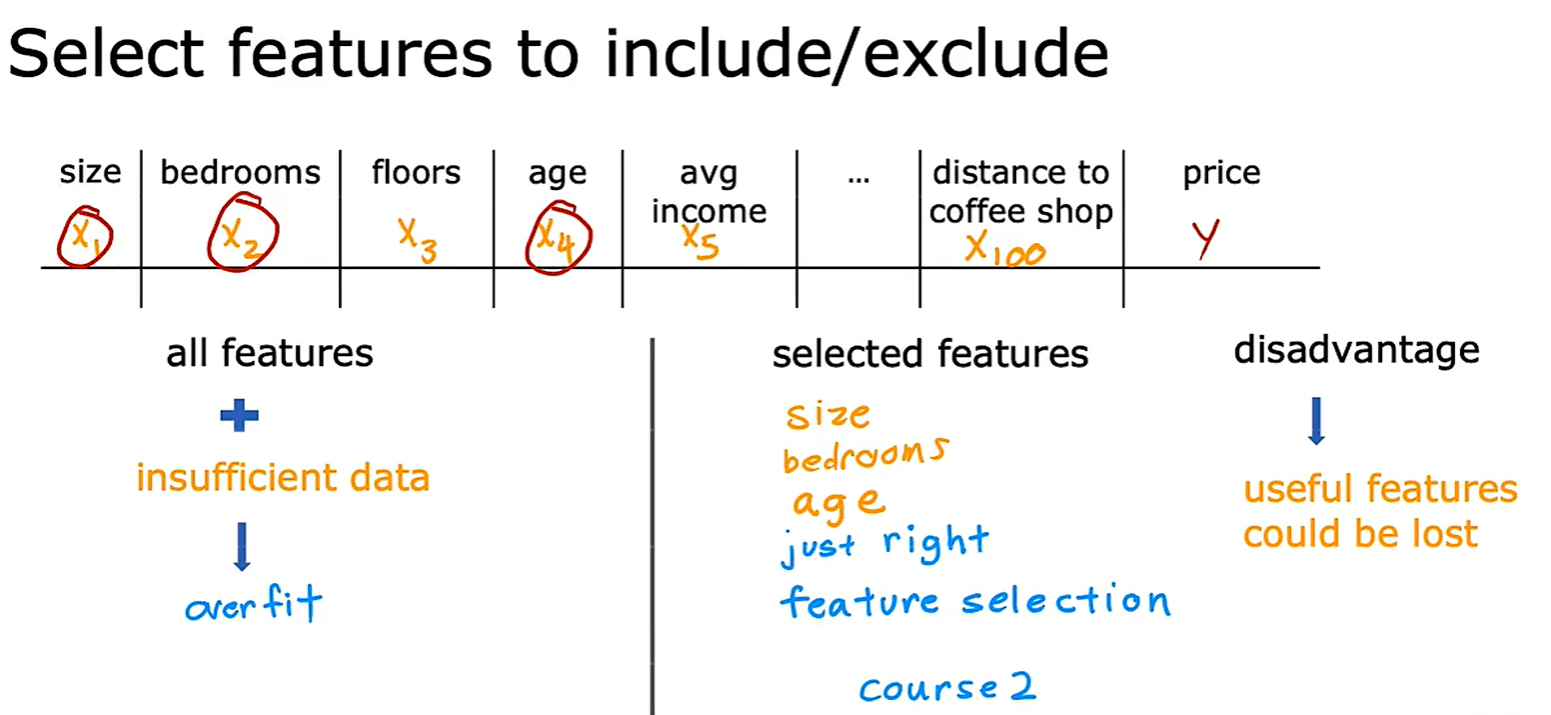
- 法二:Select featrues,选择和使用特征的一个子集
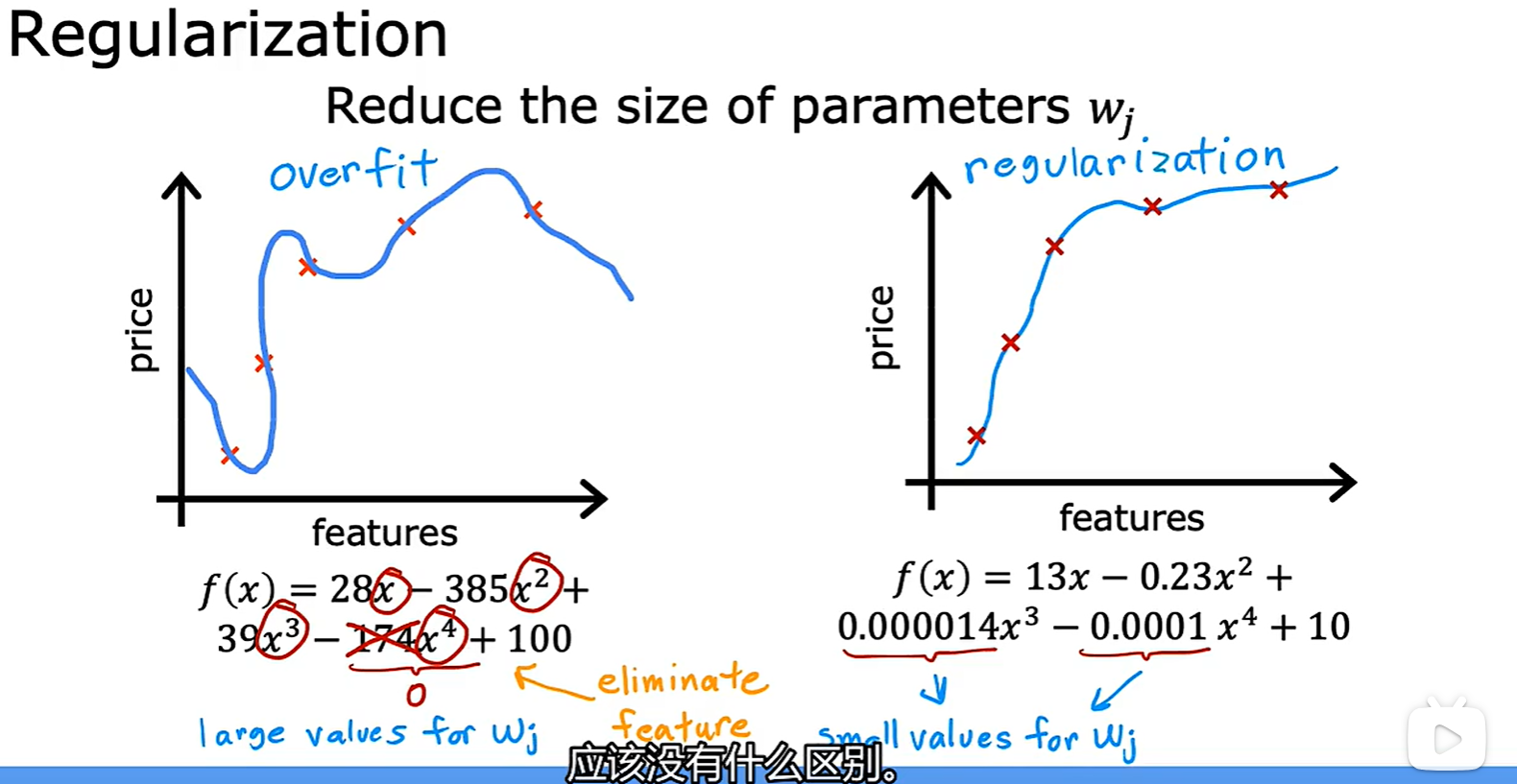
- 法三:Regularization(正则化),减小参数大小;通常是改变 Wi 的大小,而不改变 b;
3.3 Regularization
- 增加了
这个参数,为了降低损失函数,需要调节它的值,可以起到减小参数的作用;

Regularized linear regression
- 正则化线性回归中的梯度下降:

- 原理:每次迭代 Wj 都乘一个略小于 1 的数,用于缩小参数;

Regularized logistic regression