快速幂
前言
这些是数学相关的算法,理解一下思路,记一下模板代码即可,多用于数据处理,即解题中的某一步。
问题引入

- 根据以往的学习经验,我们在计算5的10次方这个问题时,需要多少次的运算呢?
一般来说你可能会想到for循环次方数 ,一直累乘,这样算的时间复杂度为O(n)
那么对于这种运算,我们能否对其进行优化 ,从而缩短运算时间呢?
解决过程
- 我们很容易发现,10个5相乘是一个完全重复的过程,如果它变成(5×5)×(5×5)×(5×5)×(5×5)×(5×5),因为我们把5*5这个重复的运算先完成了,这样运算次数缩短为5次 。
继续下去可以发现(5×5)×(5×5)也是重复进行的。
如果我们进一步优化,那么就可以变成(5×5×5×5)×(5×5×5×5)×(5×5)。 - 由上面可以知道的是(5×5×5×5)就是(5×5)的平方(5×5)又是5的平方,那么这个过程就变为了:一个数字始终在平方,当你需要它的时候就取它的值 。

比如我要计算510,那么我需要取2个数的值:52的值和58的值,因为52×58=510
问题产生及解决
- 取值怎么取,是固定的吗?比如能不能取53的值和57的值?
答:不能。上面推理的时候我们是两两合为一个,比如5×5×5×5合成为(5×5)×(5×5),(5×5)×(5×5)又合成为(5×5×5×5),也就是上面的一句话:一个数字始终在平方,当你需要它的时候就取它的值 ,也就是说,我们取的数一定是2的幂次数。为什么?方便以后复用 。复用就是比如54由前面已经得到的52经过乘以自己 (即52×52)得到。
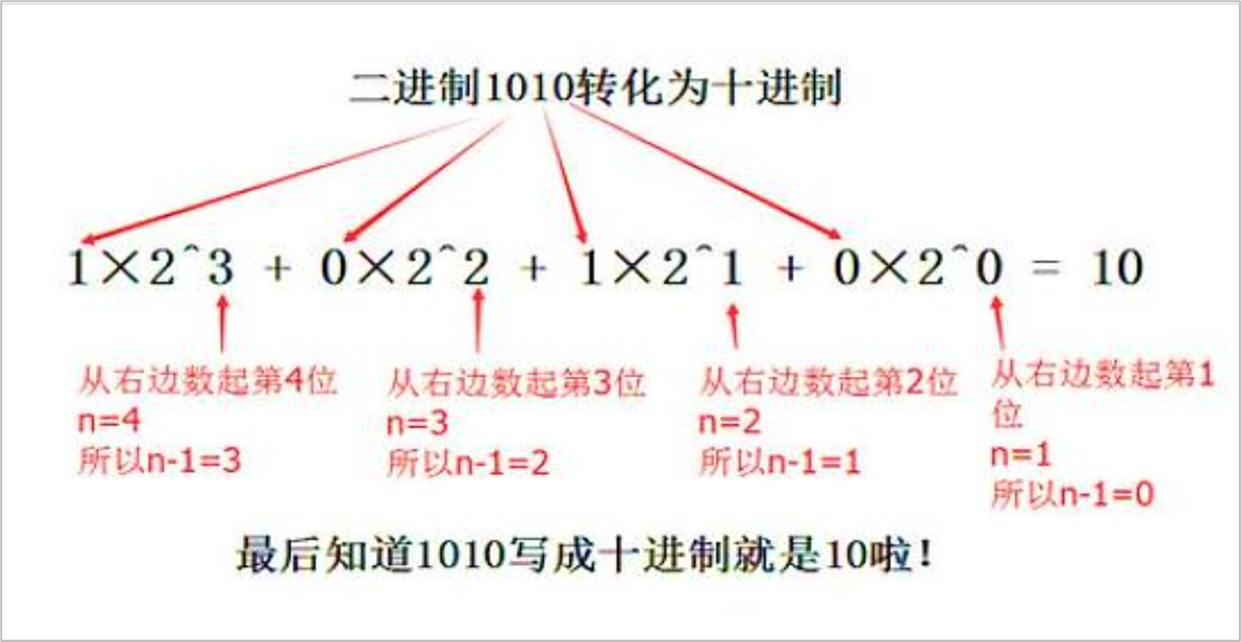
- 既然要得到2的幂累积和的形式,也就是我们把一个十进制的次方数转成了二进制,怎么转?
答:进制转换:任何数都可以写成2^n相加的形式。
5=22+20;
7=22+21+20;
为什么?
除基取余法 。

做法
- 此时我们结合进制转换的知识,把幂数拆成了几个2的幂累和的形式,也就是我们把一个十进制的次方数转成了二进制,但是不直接写成二进制形式而是把二进制形式里为1的部分,写出来做累加。
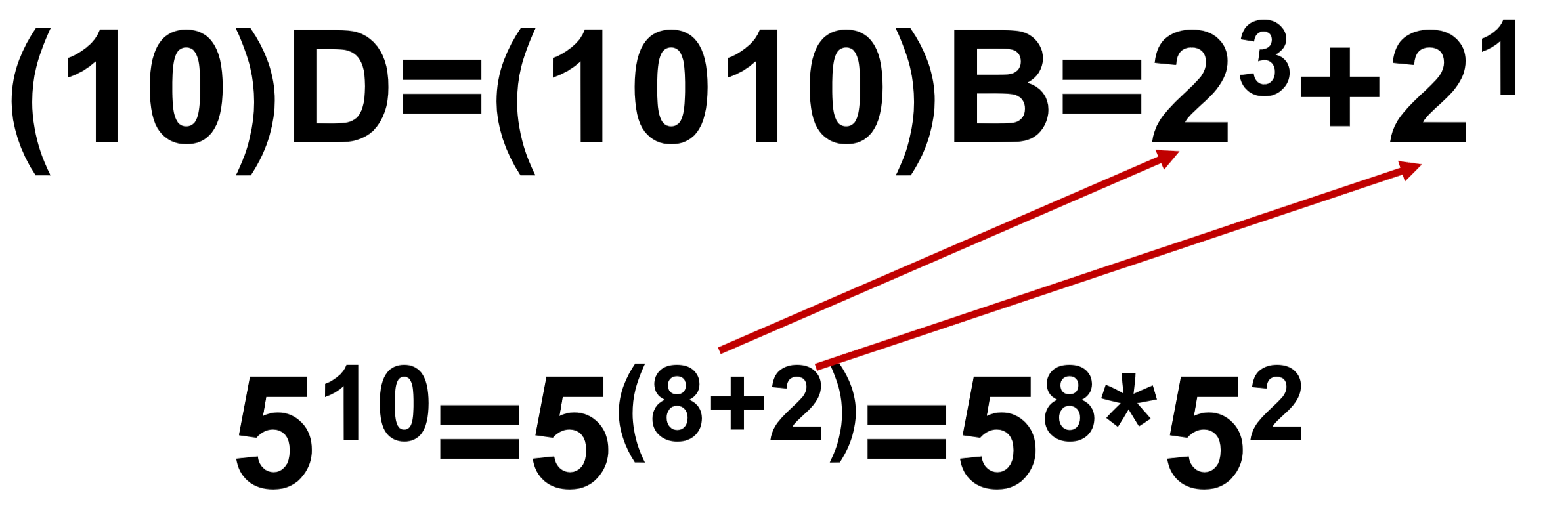
- 58,52如何求?
5不断平方:51 52 54 58 516
计算nx:
- 任务一 :有一个变量 始终保存当前是2的几次方,即20、21、22以此类推,如果我们以n作为底数,那么到此题中就变成了n1、n2、n4,我们只需要每次n*=n即可
- 任务二 :如果x%2==1证明该二进制位的值为1,因此应该用累乘变量res乘上当前的n。当然在循环的最后,和10进制转2进制一样,x需要除以2,只要x不为零这个循环始终执行下去
代码:
c
int n,x; //底数,次方数
int res=1; //累乘变量
int main(){
scanf("%d %d",&n,&x);
while(x!=0){ //只要x不为0就始终执行下去
int j=x%2;
if(j==1){
res*=n; //当前2进制位为1,乘上当前位置的n,即我们的任务二
}
x/=2; //x除以2,和短除法一样
n*=n; //n每次乘以自身,即我们的任务一
}
printf("%d\n",res);
return 0;
}时间复杂度:O(log x)
以510为例:
10的二进制 为1010,即1×23+0×22+1×21+0×20,根据代码,当任务一持续执行时 ,在第二位和第四位执行代码res*=n(即任务二);在第二位时,n=52。在第四位时,n=58。52×58=510,代码结束。
第一轮:
j=10%2=0;(任务二不执行)
x=10/2=5;(x不为0,程序继续执行任务一)
n=5×5=52;(任务一)
第二轮:
j=5%2=1;(任务二执行)
res=1×52=52;(任务二)
x=5/2=2;(x不为0,程序继续执行任务一)
n=52×52=54;(任务一)
第三轮:
j=2%2=0;(任务二不执行)
x=2/2=1;(x不为0,程序继续执行任务一)
n=54×54=58;(任务一)
第四轮:
j=1%2=1;(任务二执行)
res=52×58=510;(任务二)
x=1/2=0;(x为0,程序结束任务一不执行)
此时输出res就是510的值.
板子题
-
如果题目提示要你把算出来的答案取余输出 ,说明算出来的答案非常大,甚至连long long都存不下,所以在计算的过程中就要把取摸运算加上去,不要想着等算出答案再取摸(要保证每一步都能用正常的数据类型存的下)。
-
在计算过程中取余遵循下面的模运算理论:
(a×b)%c=( (a%c) × (b%c) )%c
加法同理
(a+b)%c=(a%c+b%c)%c
证明如下:
证明 (a×b)%c= ( (a%c) × (b%c) ) % c
令:
a%c=y ------>a= i×c + y (i为常数)
b%c=z ------>b= j×c + z (j为常数)
有:
(a×b)%c= ( (i×c+y) × (j×c+z) ) % c ·····················①
(i×c+y) × (j×c+z)= i×j×c× c + i×z× c + j×y× c + y×z
······················= (i×j×c×i×z×j×y )×c + y×z
令:
i×j×c×i×z×j×y =k则有:
(i×c + y) × (j×c + z)= k×c + y×z ··························②
把②代入①式:
(a×b)%c= (k×c + y×z)%c
···········=(k×c)%c + (y×z)%c
···········=0 + (y×z)%c
把y,z展开:
(a×b)%c=0 + ( (a%c) × (b%c) )%c
证毕.