【算法基础篇】（四十五）裴蜀定理与扩展欧几里得算法：从不定方程到数论万能钥匙

前言

在算法竞赛的数论版图中，裴蜀定理和扩展欧几里得算法是解决 "线性不定方程""同余方程""乘法逆元" 等核心问题的底层支撑。它们如同数论中的 "万能钥匙"，不仅能判定方程是否有解，还能精准求出解的具体形式，更是后续学习中国剩余定理、模运算优化等高级内容的基础。本文将从定理本质出发，层层拆解裴蜀定理的核心逻辑、扩展欧几里得算法的推导过程，手把手教你掌握从理论到实战的全流程，让你在不定方程和同余问题中轻松破局。下面就让我们正式开始吧！

一、裴蜀定理：不定方程有解的 "判定准则"

1.1 定理的核心表述

裴蜀定理（又称贝祖定理）是数论中关于线性不定方程的基础定理，其核心表述为：

对于任意整数 a、b，一定存在整数 x、y，使得 ax+by=gcd(a,b)。

其中 gcd(a,b) 表示 a 和 b 的最大公约数。这个定理看似简单，却揭示了线性不定方程有解的本质条件 ------ 方程 ax+by=c 有整数解的充要条件是 gcd(a,b)∣c（即 c 能被 a 和 b 的最大公约数整除）。

直观示例验证

取 a=6，b=8：gcd(6,8)=2，根据裴蜀定理，存在整数 x、y 使得 6x+8y=2。例如 x=−1，y=1（6×(−1)+8×1=2）；

取 a=5，b=7：gcd(5,7)=1，存在整数 x=3，y=−2 使得 5×3+7×(−2)=1；

反例：方程 6x+8y=3 无解，因为 gcd(6,8)=2 不能整除 3。

1.2 定理的重要推论

裴蜀定理可以推广到多个整数的情况，其核心推论有两个，是解决复杂问题的关键：

二元推广 ：对于整数 a、b 和任意整数 n，一定存在整数 x、y 使得 ax+by=gcd(a,b)×n。这意味着，线性不定方程 ax+by=c 有解的充要条件是 gcd(a,b)∣c；

多元推广：对于整数 a1,a2,...,ak，一定存在整数 x1,x2,...,xk 使得 a1x1+a2x2+...+akxk=gcd(a1,a2,...,ak)×n（n 为整数）。

推论的实际意义

以二元推广为例，当我们遇到方程 ax+by=c 时，无需盲目求解，先计算 gcd(a,b) 并判断是否能整除 c：若不能整除，直接判定无解；若能整除，再进一步求解，可大幅节省时间。

1.3 定理的关键注意点

正负性不影响 ：a、b 的正负对定理结果无影响。若 ax+by=d 有解，则 a(−x)+(−b)y=−d 也有解，只需在解的基础上调整符号即可；

解的存在性≠唯一性：裴蜀定理仅保证解的存在性，若方程有解，则一定有无穷多组解（后续扩展欧几里得算法会给出通解形式）；

gcd 的核心地位：无论 a、b 多大，方程 ax+by=c 的有解性完全由 gcd(a,b) 和 c 的整除关系决定。

1.4 实战例题：洛谷 P4549 【模板】裴蜀定理

题目链接：https://www.luogu.com.cn/problem/P4549

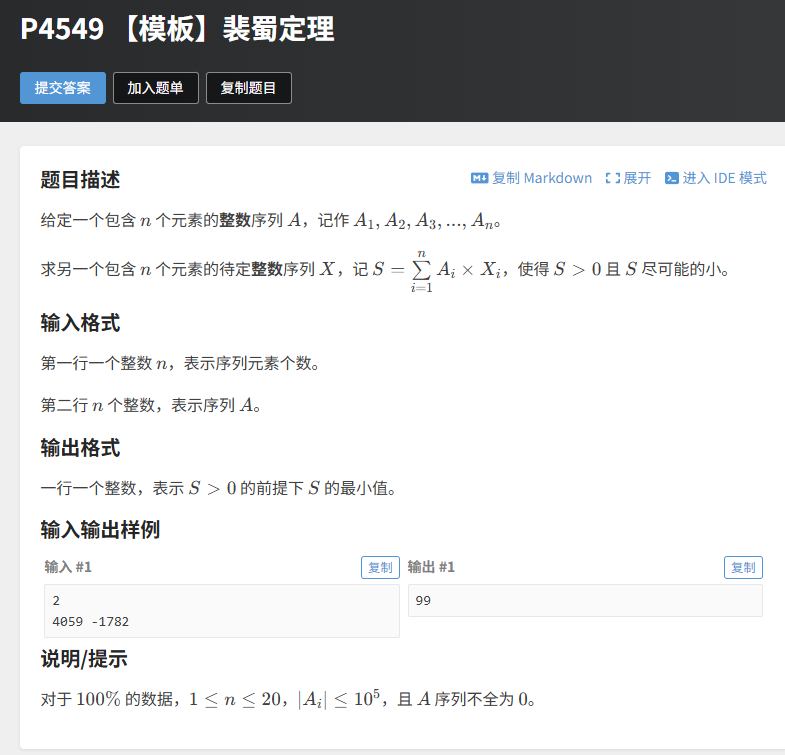
题目分析

题目描述 ：给定包含 n 个元素的整数序列 A，求另一个整数序列 X，使得且 S 尽可能小。

输入描述：第一行一个整数 n，第二行 n 个整数表示序列 A。

输出描述：一行一个整数，表示满足条件的最小 S。

示例输入：2 4059 -1782 → 输出：99。

核心思路：根据裴蜀定理的多元推广，∑i=1nAi×Xi 的所有可能结果都是 gcd(A1,A2,...,An) 的倍数。因此，最小的正结果就是所有元素的最大公约数的绝对值（因为序列中可能有负数，gcd 本身非负）。

C++ 实现

cpp 复制代码

#include <iostream>
#include <cmath>
using namespace std;

// 欧几里得算法求gcd
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n;
    cin >> n;
    int ret;
    cin >> ret;
    ret = abs(ret); // 取绝对值，避免负数影响gcd计算
    
    for (int i = 2; i <= n; ++i) {
        int x;
        cin >> x;
        ret = gcd(ret, abs(x)); // 依次计算所有元素的gcd
        if (ret == 1) break; // gcd最小为1，可提前退出
    }
    
    cout << ret << endl;
    return 0;
}

代码分析

时间复杂度 ：O(nlogM)，其中 M 是序列中元素的最大值。每次调用欧几里得算法的时间复杂度为 O(logM)，共调用 n−1 次；

关键优化：由于 gcd 的性质，当计算过程中 ret=1 时，后续元素的 gcd 不可能更小，可直接退出循环；

边界处理：序列元素可能为负，需取绝对值后再计算 gcd（gcd 的结果与输入正负无关）。

二、扩展欧几里得算法：不定方程的 "求解工具"

裴蜀定理告诉我们方程 ax+by=c 何时有解，但没有给出具体的求解方法。而扩展欧几里得算法（Extended Euclidean Algorithm）正是裴蜀定理的 "延伸"------ 它不仅能计算 a 和 b 的最大公约数，还能同时求出方程 ax+by=gcd(a,b) 的一组特解，进而推导出所有整数解。

2.1 算法的核心推导

扩展欧几里得算法的推导基于欧几里得算法（辗转相除法）的递归过程，我们通过逐步拆解来理解其逻辑：

步骤 1：欧几里得算法的递归性质

欧几里得算法的核心是 gcd(a,b)=gcd(b,a mod b)，当 b=0 时，gcd(a,0)=a。

步骤 2：递归终止条件

当 b=0 时，方程 ax+by=gcd(a,b) 简化为 ax=a，此时一组特解为 x=1，y=0（因为 a×1+0×0=a=gcd(a,0)）。

步骤 3：递归过程的解推导

假设我们已经求出了递归下一层的解：对于 gcd(b,amodb)，存在整数 x1、y1 使得：

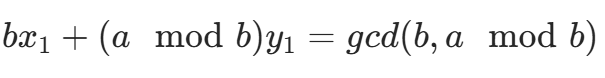
由于，代入上式得：

整理后：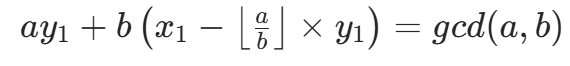

对比目标方程，可得当前层的解为：

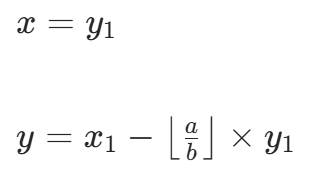
通过这种方式，我们可以从递归终止条件反向推导，逐步求出原方程的一组特解。

2.2 算法的 C++ 实现（递归版）

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;

// 扩展欧几里得算法：返回gcd(a,b)，并通过引用返回方程ax+by=gcd(a,b)的一组特解(x,y)
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        // 递归终止条件：b=0时，x=1，y=0
        x = 1;
        y = 0;
        return a;
    }
    // 递归计算下一层
    LL x1, y1, d;
    d = exgcd(b, a % b, x1, y1);
    // 推导当前层的解
    x = y1;
    y = x1 - (a / b) * y1;
    return d;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL a = 6, b = 8;
    LL x, y;
    LL d = exgcd(a, b, x, y);
    cout << "gcd(" << a << ", " << b << ") = " << d << endl;
    cout << "方程 " << a << "x + " << b << "y = " << d << " 的一组特解：x = " << x << ", y = " << y << endl;
    // 输出：gcd(6,8)=2；特解x=-1, y=1（6*(-1)+8*1=2）
    return 0;
}

2.3 算法的非递归实现（可选）

递归实现简洁直观，但对于极端数据（如 a、b 达到 1e18）可能导致栈溢出。以下是非递归版本的实现，逻辑与递归版一致：

python 复制代码

#include <iostream>
using namespace std;

typedef long long LL;

LL exgcd_non_recursive(LL a, LL b, LL& x, LL& y) {
    LL x0 = 1, y0 = 0; // 初始状态：b=0时的解
    LL x1 = 0, y1 = 1; // 初始状态：a=b, b=a%b时的解
    x = 0, y = 1;
    LL d = a;
    while (b != 0) {
        LL q = a / b; // 商
        LL r = a % b; // 余数
        // 更新a和b
        a = b;
        b = r;
        // 更新解
        LL tx = x;
        LL ty = y;
        x = x0 - q * x1;
        y = y0 - q * y1;
        x0 = x1;
        y0 = y1;
        x1 = tx;
        y1 = ty;
    }
    x = x0;
    y = y0;
    return a;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL a = 6, b = 8;
    LL x, y;
    LL d = exgcd_non_recursive(a, b, x, y);
    cout << "gcd(" << a << ", " << b << ") = " << d << endl;
    cout << "特解：x = " << x << ", y = " << y << endl;
    return 0;
}

2.4 通解的推导

扩展欧几里得算法求出的是方程 ax+by=gcd(a,b) 的一组特解 (x0,y0)，但方程的解有无穷多个。我们可以通过特解推导出所有整数解（通解）：

设 d=gcd(a,b)，令 a′=da，b′=db（此时 a′ 和 b′ 互质）。对于方程 ax+by=d，其通解为：x=x0+k⋅b′(k∈Z)y=y0−k⋅a′(k∈Z)

通解推导逻辑

由于 a′x0+b′y0=1（两边除以 d 得到），代入通解：

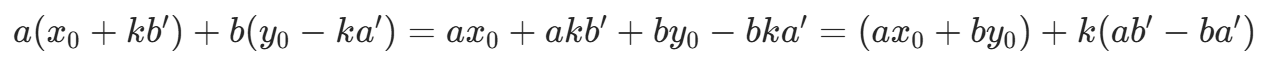
由于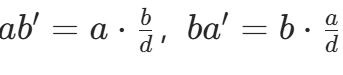，因此 ab′−ba′=0，原式等于 ax0+by0=d，满足方程。

2.5 方程 ax+by=c 的求解流程

当方程 ax+by=c 有解（即 d∣c，d=gcd(a,b)）时，求解流程如下：

用扩展欧几里得算法求出方程 ax+by=d 的一组特解 (x0,y0)；

将特解缩放 k=dc 倍，得到原方程的一组特解：x1=x0⋅k，y1=y0⋅k；

原方程的通解为：x=x1+k⋅db(k∈Z)y=y1−k⋅da(k∈Z)

示例：求解 6x+8y=4

计算 d=gcd(6,8)=2，c=4，k=4/2=2；

求出 6x+8y=2 的特解 (x0=−1,y0=1)；

原方程特解：x1=−1×2=−2，y1=1×2=2（6×(−2)+8×2=−12+16=4，正确）；

通解：x=−2+4k，y=2−3k（k 为整数）。

三、实战例题 3：洛谷 P5656 【模板】二元一次不定方程 (exgcd)

题目链接：https://www.luogu.com.cn/problem/P5656

3.1 题目分析

题目描述：给定不定方程 ax+by=c，判断是否有整数解。若无解，输出 −1；若有解但无正整数解（x>0，y>0），输出 x 和 y 的最小正整数值；若有正整数解，输出正整数解的个数、x 的最小值、y 的最小值、x 的最大值、y 的最大值。

输入描述：第一行一个整数 T，每组数据一行三个正整数 a、b、c。

输出描述：按题目要求输出对应结果。

示例输入：7 2 11 100 → 输出：4 6 2 39 8。

核心难点：

从通解中筛选出正整数解，并计算解的个数和极值；

处理 x 或 y 为 0 的情况（0 不是正整数）；

避免数值溢出，需使用长整型。

3.2 解题思路

用扩展欧几里得算法判断方程是否有解（c%d==0），无解则输出 −1；

有解则求出特解，并推导通解；

计算 x 的最小正整数值，进而求出对应的 y，判断是否为正整数：

若 y>0，则存在正整数解，计算解的个数和其他极值；

若 y≤0，则无正整数解，输出 x 和 y 的最小正整数值。

关键公式推导

设通解为：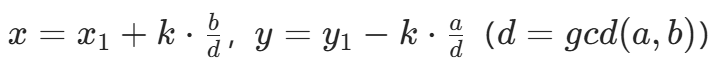

x 的最小正整数值：，若结果为 0 则取 k1；

代入 xmin 求出对应的 y，若 y>0，则 y max=y；

y 的最小正整数值：，若结果为 0 则取 k2；

代入 y min 求出对应的 x，即为 x max；

正整数解的个数：。

3.3 C++ 实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;

// 扩展欧几里得算法
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d;
    d = exgcd(b, a % b, x1, y1);
    x = y1, y = x1 - a / b * y1;
    return d;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int T;
    scanf("%d", &T);
    while (T--) {
        LL a, b, c;
        scanf("%lld%lld%lld", &a, &b, &c);
        LL x, y, d;
        d = exgcd(a, b, x, y);
        
        if (c % d != 0) {
            // 无解
            printf("-1\n");
            continue;
        }
        
        // 求出原方程的一组特解
        LL k = c / d;
        x = x * k, y = y * k;
        LL k1 = b / d; // x的增量
        LL k2 = a / d; // y的减量
        
        // 计算x的最小正整数值
        x = (x % k1 + k1) % k1;
        if (x == 0) x = k1;
        // 对应的y值
        y = (c - a * x) / b;
        
        LL minx, miny, maxx, maxy;
        if (y > 0) {
            // 存在正整数解
            minx = x;
            maxy = y;
            // 计算y的最小正整数值
            y = (y % k2 + k2) % k2;
            if (y == 0) y = k2;
            miny = y;
            // 计算x的最大正整数值
            maxx = (c - b * y) / a;
            // 计算解的个数
            LL cnt = (maxx - minx) / k1 + 1;
            printf("%lld %lld %lld %lld %lld\n", cnt, minx, miny, maxx, maxy);
        } else {
            // 无正整数解，输出x和y的最小正整数值
            minx = x;
            y = (y % k2 + k2) % k2;
            if (y == 0) y = k2;
            miny = y;
            printf("%lld %lld\n", minx, miny);
        }
    }
    return 0;
}

四、常见误区与避坑指南

4.1 数值溢出问题

误区：使用 int 类型存储大数值（如 a、b 达到 1e9），导致乘法或加法溢出；

避坑：所有变量统一使用 long long 类型，尤其是在计算 a×x、b×y 时，避免溢出。

4.2 特解缩放错误

误区：求解 ax+by=c 时，忘记将特解缩放 k=c/d 倍；

反例：方程 6x+8y=4，若直接使用 6x+8y=2 的特解 (−1,1)，会得到 6×(−1)+8×1=2=4；

避坑：牢记 "特解缩放" 步骤，确保解满足目标方程。

4.3 最小正整数解计算错误

误区：将特解直接取模后未处理负数情况；

反例：特解 x=−1，b/d=4，直接取模得 −1%4=−1，并非最小正整数解；

避坑：使用公式 (x%k+k)%k（k=b/d），确保结果为正整数。

4.4 通解增量搞反

误区：混淆通解中 x 和 y 的增量 / 减量；

避坑：牢记通解公式：x 的增量为 b/d，y 的减量为 a/d，二者符号相反。

4.5 忽略方程转化时的符号

误区：将同余方程 ax ≡ b(mod m) 错误转化为 ax+my=b（正确应为 ax−my=b）；

避坑：严格按照同余定义进行转化，确保方程等价性。

总结

如果在学习过程中遇到具体题目无法解决，或想了解乘法逆元、中国剩余定理等延伸知识点，可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！

【算法基础篇】（四十五）裴蜀定理与扩展欧几里得算法：从不定方程到数论万能钥匙

目录

前言

一、裴蜀定理：不定方程有解的 "判定准则"

1.1 定理的核心表述

直观示例验证

1.2 定理的重要推论

推论的实际意义

1.3 定理的关键注意点

1.4 实战例题：洛谷 P4549 【模板】裴蜀定理

题目分析

C++ 实现

代码分析

二、扩展欧几里得算法：不定方程的 "求解工具"

2.1 算法的核心推导

步骤 1：欧几里得算法的递归性质

步骤 2：递归终止条件

步骤 3：递归过程的解推导

2.2 算法的 C++ 实现（递归版）

2.3 算法的非递归实现（可选）

2.4 通解的推导

通解推导逻辑

2.5 方程 ax+by=c 的求解流程

示例：求解 6x+8y=4

三、实战例题 3：洛谷 P5656 【模板】二元一次不定方程 (exgcd)

3.1 题目分析

3.2 解题思路

关键公式推导

3.3 C++ 实现

四、常见误区与避坑指南

4.1 数值溢出问题

4.2 特解缩放错误

4.3 最小正整数解计算错误

4.4 通解增量搞反

4.5 忽略方程转化时的符号

总结