题目描述

提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109
解题思路一
暴力解
头到尾遍历整个数组。
用一个变量 first 记录第一次遇到 target 的索引。
继续遍历,用另一个变量 last 不断更新最后一次遇到 target 的索引。
如果遍历结束后 first 仍然是初始值(例如 -1),说明目标值不存在,返回 [-1, -1]。
否则,返回 [first, last]。
代码实现:
c
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
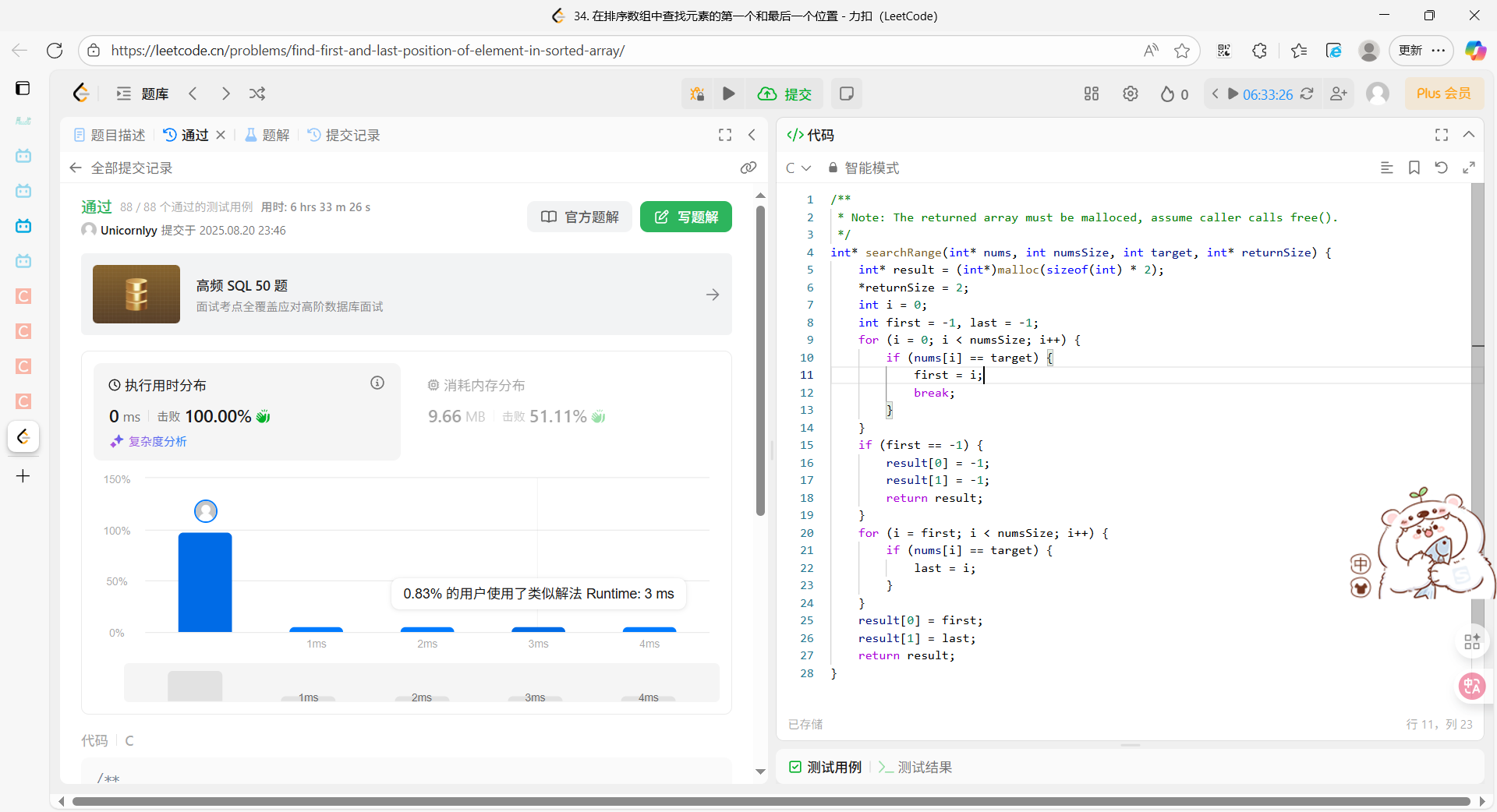
int* searchRange(int* nums, int numsSize, int target, int* returnSize) {
int* result = (int*)malloc(sizeof(int) * 2);
*returnSize = 2;
int i = 0;
int first = -1, last = -1;
for (i = 0; i < numsSize; i++) {
if (nums[i] == target) {
first = i;
break;
}
}
if (first == -1) {
result[0] = -1;
result[1] = -1;
return result;
}
for (i = first; i < numsSize; i++) {
if (nums[i] == target) {
last = i;
}
}
result[0] = first;
result[1] = last;
return result;
}执行结果:
cpp
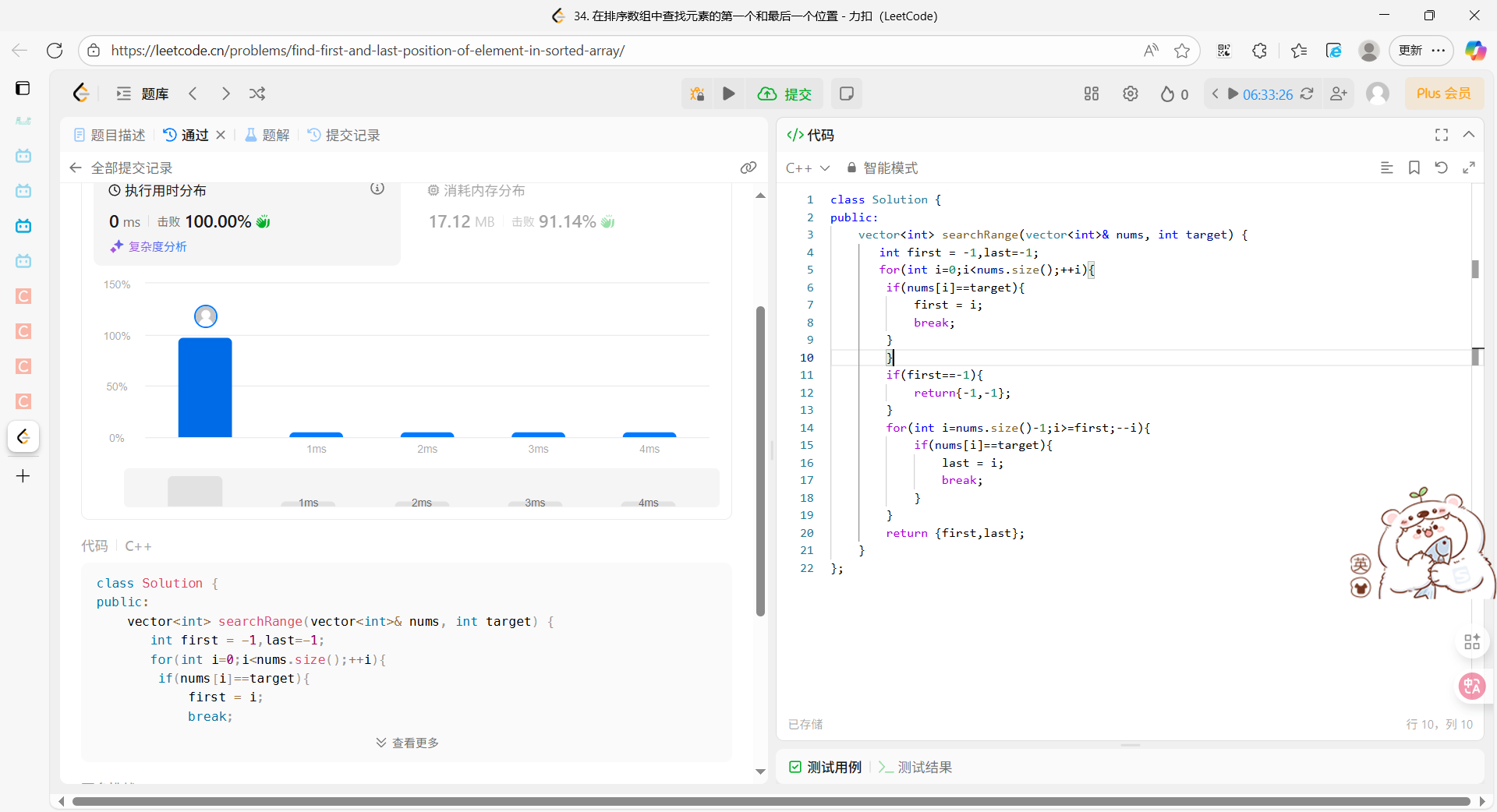
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int first = -1,last=-1;
for(int i=0;i<nums.size();++i){
if(nums[i]==target){
first = i;
break;
}
}
if(first==-1){
return{-1,-1};
}
for(int i=nums.size()-1;i>=first;--i){
if(nums[i]==target){
last = i;
break;
}
}
return {first,last};
}
};
复杂度分析:
时间复杂度:O(n)
空间复杂度:O(1)
解法二:二分查找
两次二分查找是最优解
一次查找用于定位第一个等于 target 的位置(左边界)。
另一次查找用于定位最后一个等于 target 的位置(右边界)。
.1 查找左边界(First Position)
我们需要修改二分查找的逻辑,使得当 nums[mid] == target 时,我们不立即返回,而是尝试在左半部分继续寻找,看看有没有更靠前的 target。
具体步骤:
初始化 left = 0, right = n-1, first_pos = -1。
初始化 left = 0,right = n-1,first_pos = -1。
进入 while (left <= right) 循环。
输入 while(left <= right) 循环。
计算 mid = left + (right - left) / 2。
计算 mid = left +(right - left)/ 2。
关键逻辑:
如果 nums[mid] > target,说明目标值在左侧,right = mid - 1。
如果 nums[mid] < target,说明目标值在右侧,left = mid + 1。
如果 nums[mid] == target,我们找到了一个 target。但它不一定是第一个。所以我们先将这个位置记录下来 first_pos = mid,然后继续在左半部分搜索,即 right = mid - 1,试图找到一个更小的索引。
循环结束后,first_pos 中存储的就是第一个目标值的位置。
2.2 查找右边界(Last Position)
逻辑与查找左边界非常相似,只是当找到 target 时,我们尝试在右半部分继续寻找。
具体步骤:
初始化 left = 0, right = n-1, last_pos = -1。
初始化 left = 0,right = n-1,last_pos = -1。
进入 while (left <= right) 循环。
输入 while(left <= right) 循环。
计算 mid = left + (right - left) / 2。
计算 mid = left +(right - left)/ 2。
关键逻辑:
如果 nums[mid] > target,说明目标值在左侧,right = mid - 1。
如果 nums[mid] < target,说明目标值在右侧,left = mid + 1。
如果 nums[mid] == target,我们找到了一个 target。但它不一定是最后一个。所以我们先将这个位置记录下来 last_pos = mid,然后继续在右半部分搜索,即 left = mid + 1,试图找到一个更大的索引。
循环结束后,last_pos 中存储的就是最后一个目标值的位置。
最终:先执行查找左边界的二分,如果没找到(返回-1),直接返回 [-1, -1]。如果找到了,再执行查找右边界的二分,最后将两个结果组合成 [first_pos, last_pos] 返回。
代码实现:
cpp
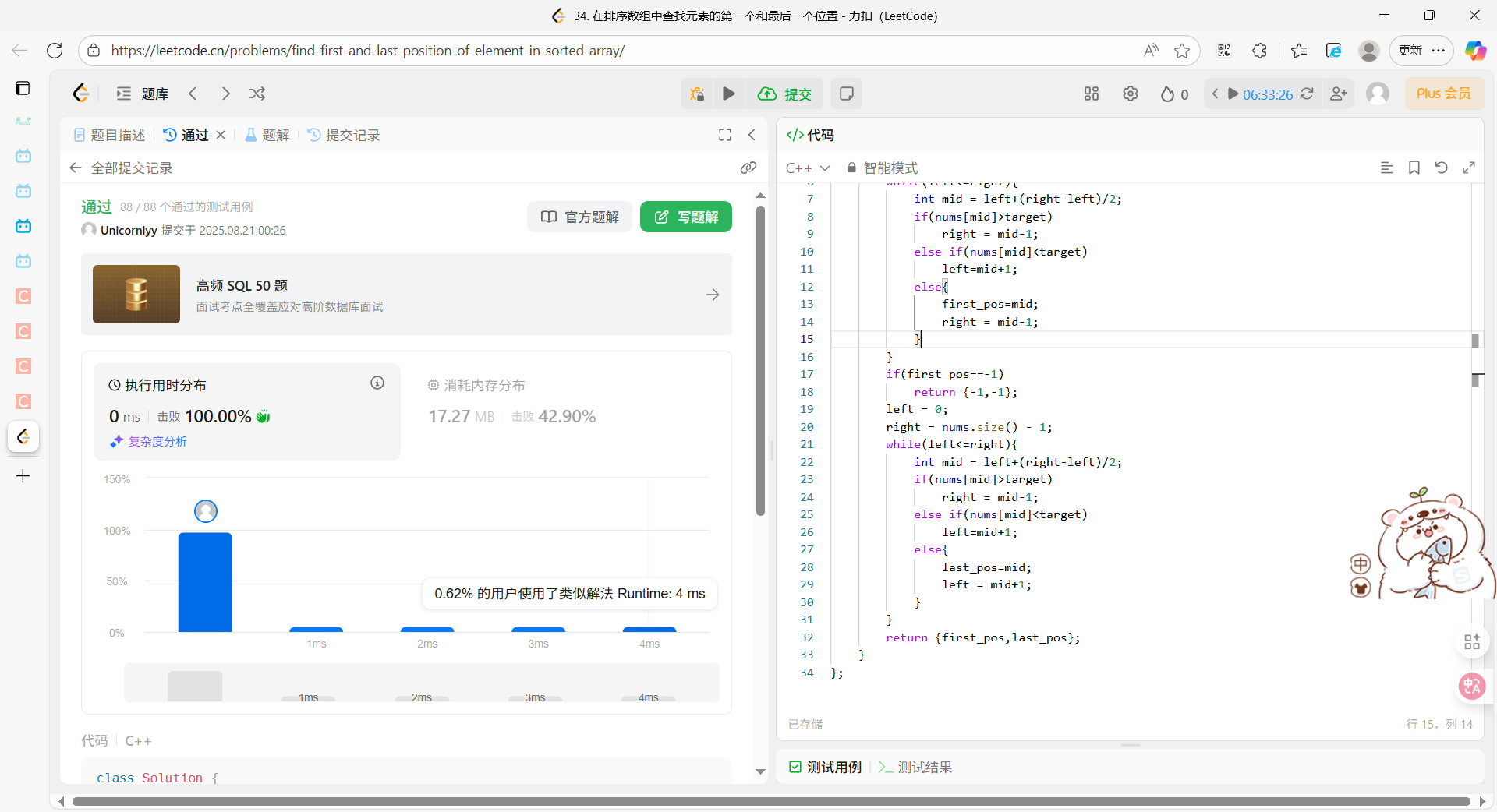
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int first_pos= -1, last_pos = -1;
int left=0,right=nums.size()-1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]>target)
right = mid-1;
else if(nums[mid]<target)
left=mid+1;
else{
first_pos=mid;
right = mid-1;
}
}
if(first_pos==-1)
return {-1,-1};
left = 0;
right = nums.size() - 1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]>target)
right = mid-1;
else if(nums[mid]<target)
left=mid+1;
else{
last_pos=mid;
left = mid+1;
}
}
return {first_pos,last_pos};
}
};执行结果
复杂度分析:
时间复杂度:O(logn)
空间复杂度:O(1)
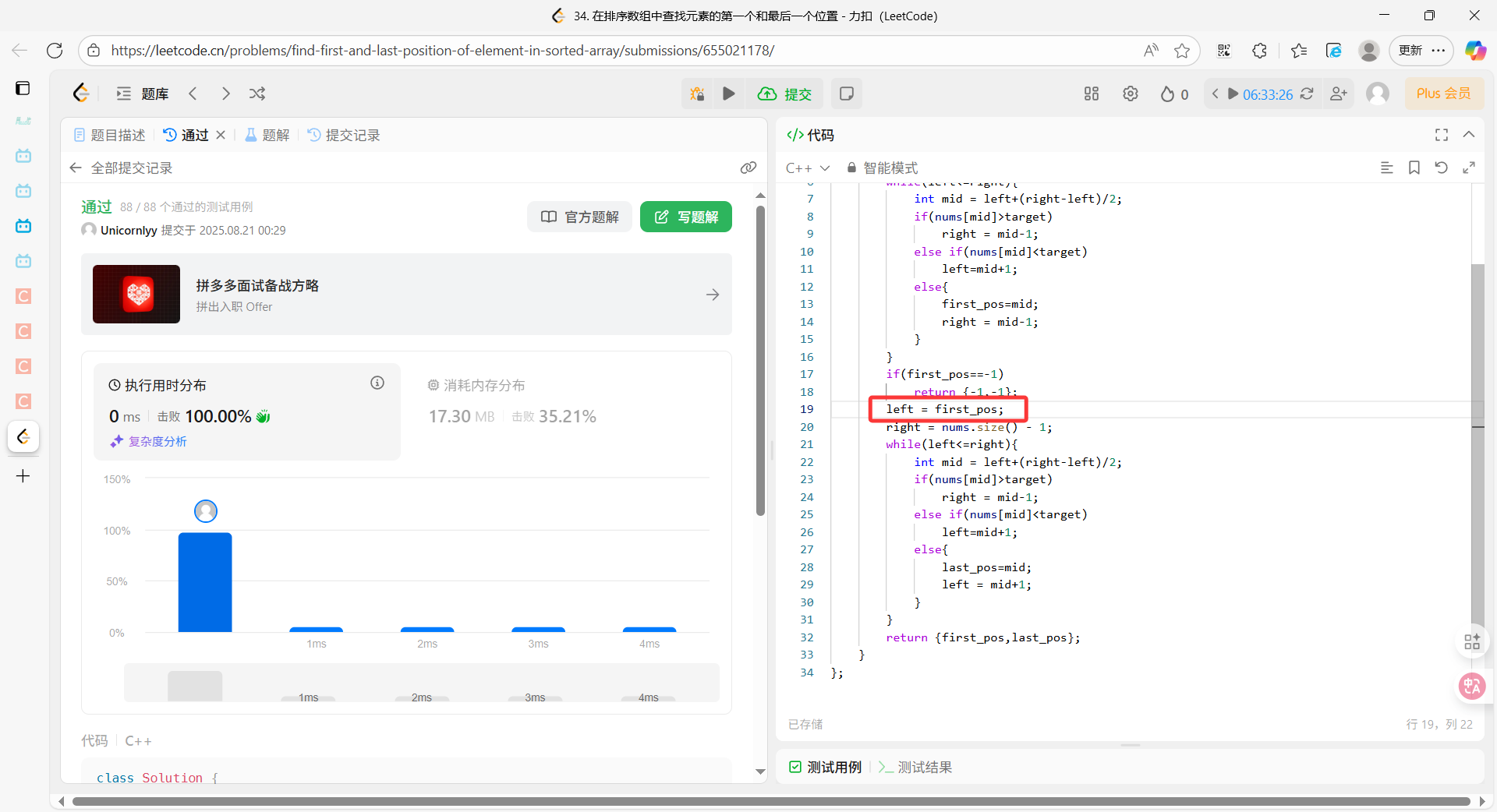
优化在第二次while循环时,只在 [first_pos, n-1] 范围内搜索而不是从【0,n-1】
思路三
巧用二分查找寻找边界(思路二的变体)
这个思路更加巧妙,它将问题转化为**"寻找第一个大于等于 target 的位置"** 和 "寻找第一个大于 target 的位置"。
寻找左边界:
我们执行一次二分查找,目的是找到第一个大于或等于 target 的元素的索引。这个索引就是我们要的左边界 left_bound。
这个查找过程也被称为 lower_bound。
寻找右边界:
我们再执行一次二分查找,目的是找到第一个大于 target 的元素的索引。
那么,这个索引减一,就是我们要的右边界 right_bound。
这个查找过程也被称为 upper_bound。
验证结果:
在找到 left_bound 后,需要检查一下 nums[left_bound] 是否真的等于 target。如果不是,或者 left_bound 越界了,说明 target 根本不存在,直接返回 [-1, -1]
cpp
#include <iostream>
#include <vector>
class Solution {
public:
std::vector<int> searchRange(std::vector<int>& nums, int target) {
int first = -1;
int last = -1;
// 寻找第一个位置
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == target) {
first = i;
break; // 找到第一个就停止
}
}
// 如果找不到,直接返回
if (first == -1) {
return {-1, -1};
}
// 寻找最后一个位置
// 从后往前找会更高效
for (int i = nums.size() - 1; i >= first; --i) {
if (nums[i] == target) {
last = i;
break; // 找到第一个(从后往前看)就停止
}
}
return {first, last};
}
};
复杂度分析:
时间复杂度:O(logn)
空间复杂度:O(1)
ok,see you next time~