【cs336学习笔记】[第6课]内核优化与Triton框架应用

小饼干超人2025-08-25 13:05

文章目录

课程内容：

  1. 介绍基准测试和性能分析的基础知识
  2. 展示用C++编写cuda内核
  3. 介绍triton框架的使用

回顾GPU的原理

GPU的结构

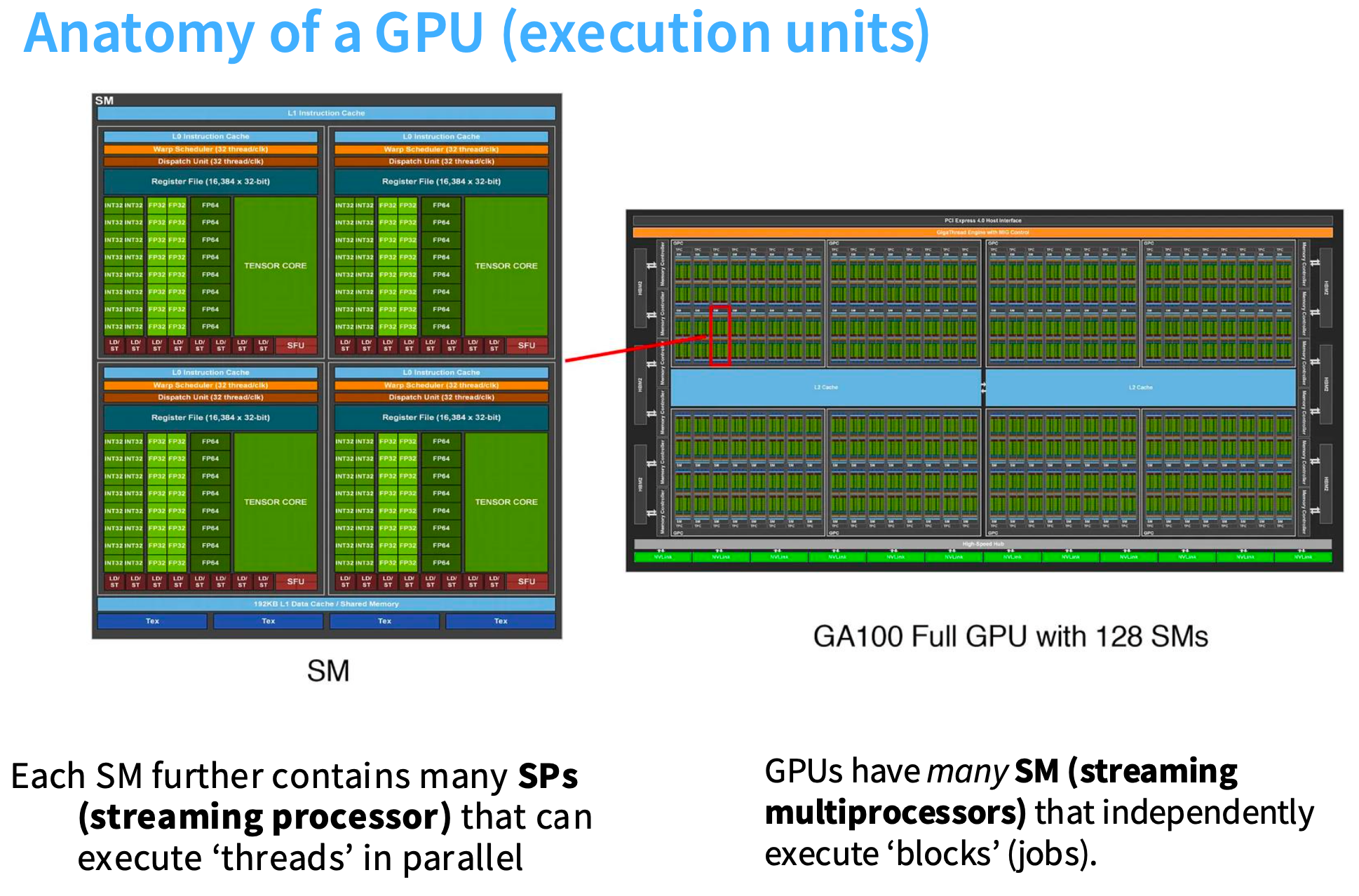
当我们拥有A100或H100这类设备时, 会有大量SM流式多处理器, 每个SM内部包含大量计算单元, 我们有FP32或FP64精度的计算单元，每个SM将启动大量线程。

我们还有内存层次结构, 其中DRAM或全局内存容量大但速度慢, 然后是更快的缓存层。

  • DRAM [A100: 80GB] - big, slow
  • L2 cache [A100: 40MB]
  • L1 cache [A100: 192KB per SM] - small, fast

有一个叫寄存器文件的组件, 运行非常快, 是每个线程可访问的内存，在编写GPU高性能代码时会大量使用这些寄存器。

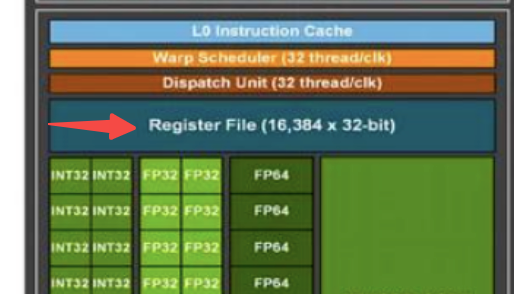
执行模型的基本结构

  • 有一组线程块, 每个块会被调度到单个SM上执行。
  • 尤其是在使用Triton等框架编写代码时, 每个块内包含大量线程, 这些线程实际执行计算任务。
  • 如果你有一个向量, 你需要对向量元素进行操作, 你会编写代码让每个线程介入, 可能同时处理向量的几个元素, 所有线程共同完成向量处理

Q：什么是线程块？

A：线程块是同时执行的线程组（wrap）。线程块存在的原因是减少控制单元需求, 因为同时执行所有线程, 在同一时间, 无需为每个线程单独控制, 只需要控制线程块组。

例如, GPU更注重计算与简化控制，所以计算单元比线程调度器多得多, 能高效并行处理无需控制。而CPU会有更多硅面积用于控制和分支预测这类功能。
Q：为什么需要线程块这种结构呢, 为什么不直接使用全局线程？

A：

  1. 线程块之间可以互相通信, 共享内存资源，在SM内部速度极快。
  2. 当你需要进行矩阵乘法时, 需要在不同线程间传递信息，在线程块内这种通信非常高效。
  3. 跨线程块或组的通信成本很高, 需要尽量将数据保留在同一线程块内, 或同一组别中, 这样能保持极高的运行速度, 这速度堪比L1缓存,
  4. 无法进行跨块同步, 因为你无法控制会发生什么

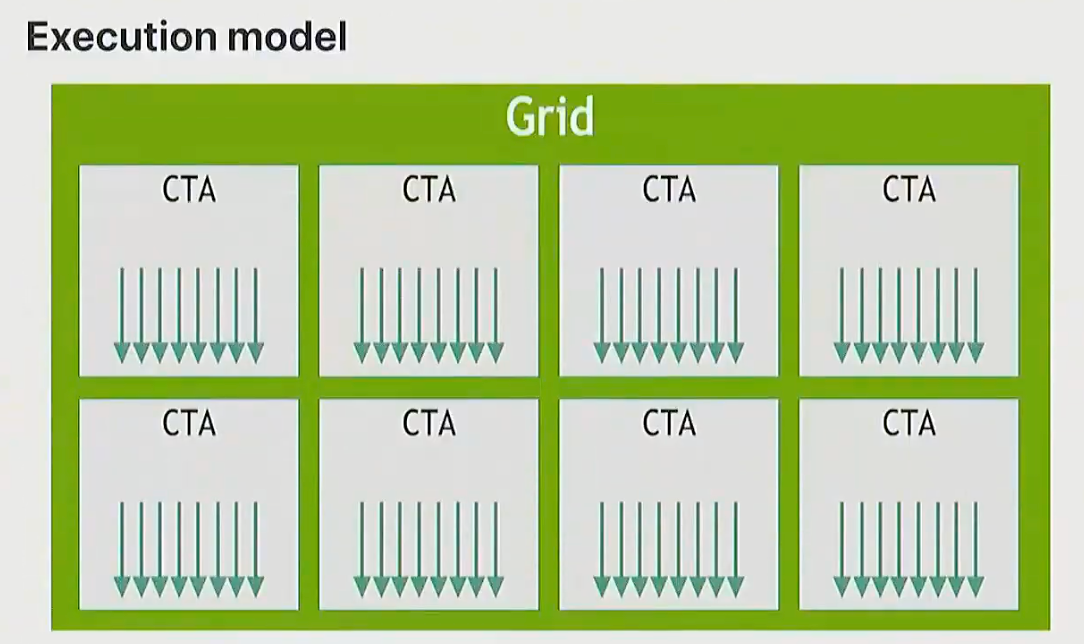
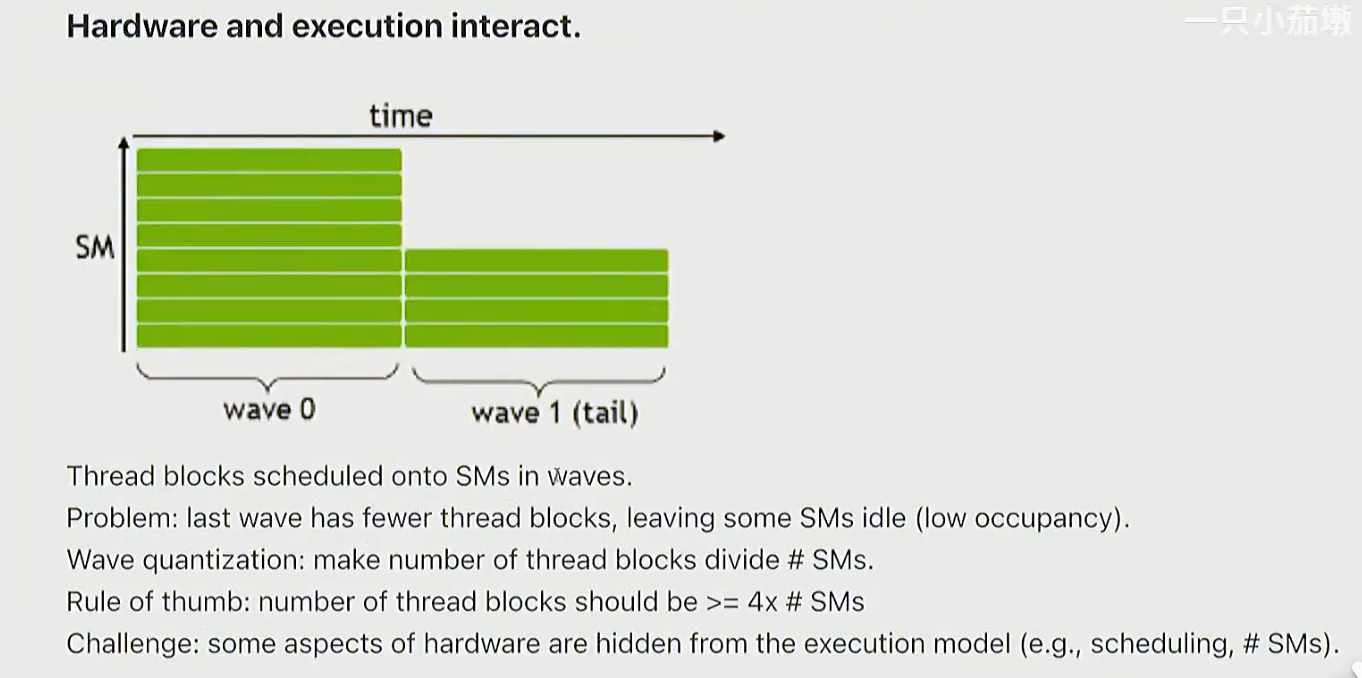
wave

线程被分组为连续的几个线程快，这就是一个波, 它们会几乎同时执行。

Q：如何确保所有波的计算量均衡？

A：调整线程块数量, 理想情况下应匹配SM数量, 并确保每个波的工作量均衡。因此我们理想情况下应有更多线程块, 并尽量实现高性能代码

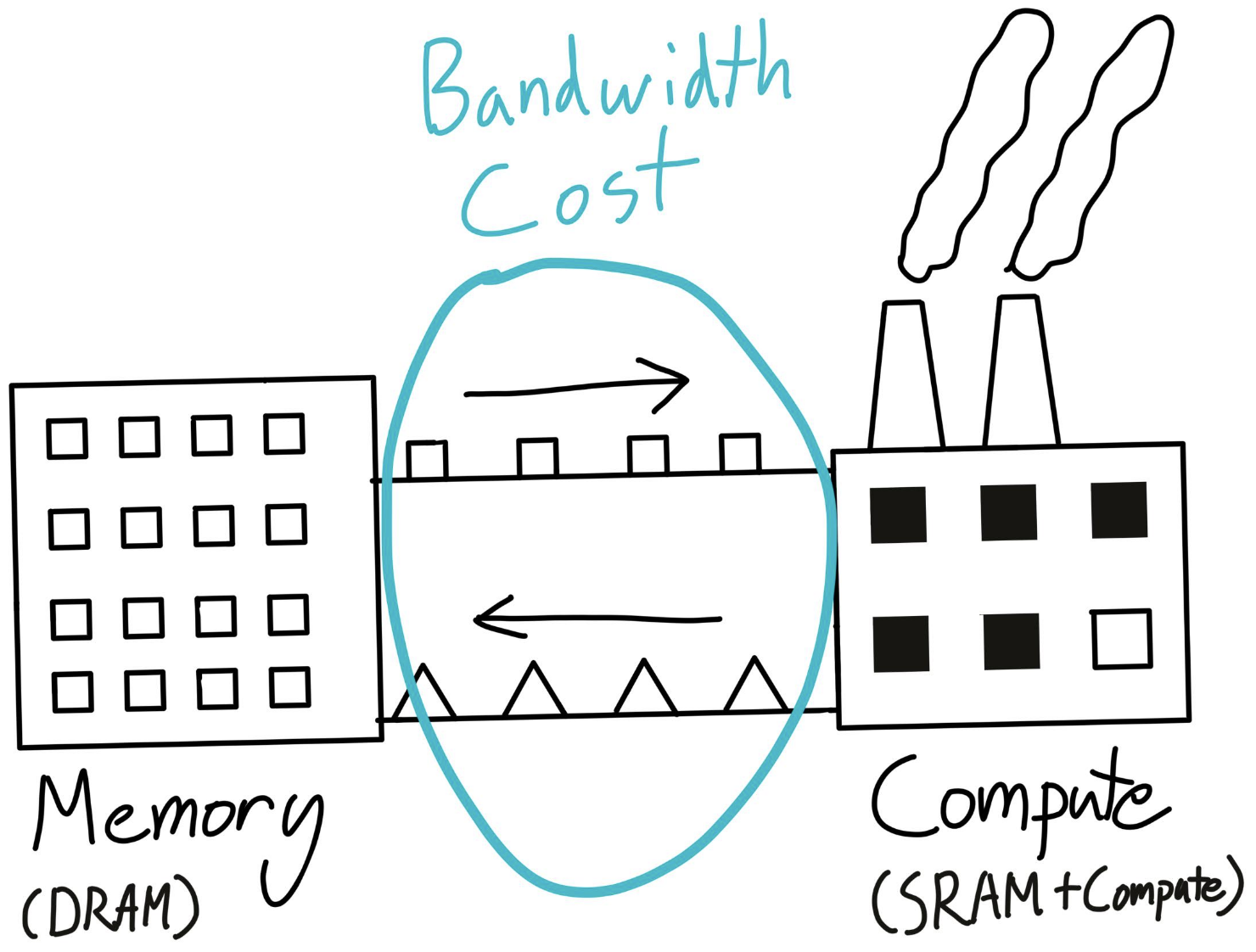
算术强度（Arithmetic Intensity: # FLOPS/ # bytes）

目标是，保持算术强度高。

即，希望浮点运算更多, 而非内存移动字节数,

因为计算扩展速度远快于内存扩展, 因此大部分时间计算会受限于内存。

基准测试

benchmark

两个重要操作：

-- warmup ：第一次执行时有很多初始化操作，使用warmup后，可以确保不测量启动速度，而是稳定状态的速度

-- torch.cuda.synchronize：确保GPU和CPU状态同步, 没有排队的任务在运行, 处于代码执行的同一阶段, 在代码执行进度上一致。

原因：

  1. CPU和GPU是计算机中的独立计算单元, 它们可以独立运行。执行模型的代码运行在CPU上，运行时会分发大量CUDA内核到GPU，GPU开始执行。而CPU会继续运行，不会等待GPU执行完成。
  2. 这对高性能代码很友好, 但基准测试时会立即发现问题。
  3. 如果你在做基准测试, 模型在GPU后台运行, CPU在做其他事情, 实际上没有测量GPU执行时间。
python 复制代码 
# https://github.com/stanford-cs336/spring2025-lectures/blob/main/lecture_06.py
def benchmark(description: str, run: Callable, num_warmups: int = 1, num_trials: int = 3):
    """Benchmark `func` by running it `num_trials`, and return all the times."""
    # Warmup: first times might be slower due to compilation, things not cached.
    # Since we will run the kernel multiple times, the timing that matters is steady state.
    for _ in range(num_warmups):
        run()
    if torch.cuda.is_available():
        torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Time it for real now!
    times: list[float] = [] # @inspect times, @inspect description
    for trial in range(num_trials):  # Do it multiple times to capture variance
        start_time = time.time()

        run()  # Actually perform computation
        if torch.cuda.is_available():
            torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

        end_time = time.time()
        times.append((end_time - start_time) * 1000) # @inspect times

    mean_time = mean(times) # @inspect mean_time
    return mean_time
将sleep传入benchmark
python 复制代码 
benchmark("sleep", lambda : time.sleep(50 / 1000))
将矩阵乘法传入benchmark
python 复制代码 
if torch.cuda.is_available():
     dims = (1024, 2048, 4096, 8192, 16384)  # @inspect dims
 else:
     dims = (1024, 2048)  # @inspect dims
 
 matmul_results = [] 
 for dim in dims:
     # @ inspect dim
     result = benchmark(f"matmul(dim={dim})", run_operation2(dim=dim, operation=lambda a, b: a @ b))
     matmul_results.append((dim, result))  # @inspect matmul_results

结论：

  1. 随着矩阵尺寸的增大，运行时间呈现超线性扩展。
  2. 在小尺寸时，时间完全没有增长。因为进行矩阵乘法存在固定开销, 这些数字需要从CPU传输到GPU。启动内核等操作也有开销, 因此并非完全超线性, 直到接近零点。但一旦矩阵足够大, 我们看到预期的扩展效果, 与我们的矩阵乘法一致。
将MLP传入benchmark
python 复制代码 
# https://github.com/stanford-cs336/spring2025-lectures/blob/main/lecture_06_mlp.py
import torch
import torch.nn as nn
import torch.cuda.nvtx as nvtx

def get_device(index: int = 0) -> torch.device:
    """Try to use the GPU if possible, otherwise, use CPU."""
    if torch.cuda.is_available():
        return torch.device(f"cuda:{index}")
    else:
        return torch.device("cpu")

class MLP(nn.Module):
    """Simple MLP: linear -> GeLU -> linear -> GeLU -> ... -> linear -> GeLU"""
    def __init__(self, dim: int, num_layers: int):
        super().__init__()
        self.layers = nn.ModuleList([nn.Linear(dim, dim) for _ in range(num_layers)])

    def forward(self, x: torch.Tensor):
        # Mark the entire forward pass
        for i, layer in enumerate(self.layers):
            # Mark each layer's computation separately
            with nvtx.range(f"layer_{i}"):
                x = layer(x)
                x = torch.nn.functional.gelu(x)
        
        return x

def run_mlp(dim: int, num_layers: int, batch_size: int, num_steps: int, use_optimizer: bool = False):
    """Run forward and backward passes through an MLP.
    
    Args:
        dim: Dimension of each layer
        num_layers: Number of linear+GeLU layers
        batch_size: Number of samples to process at once
        num_steps: Number of forward/backward iterations
        use_optimizer: Whether to use Adam optimizer for weight updates
    """
    # Define a model (with random weights)
    with nvtx.range("define_model"):
        model = MLP(dim, num_layers).to(get_device())
    
    # Initialize optimizer if requested
    optimizer = torch.optim.Adam(model.parameters()) if use_optimizer else None

    # Define an input (random)
    with nvtx.range("define_input"):
        x = torch.randn(batch_size, dim, device=get_device())

    # Run the model `num_steps` times
    for step in range(num_steps):
        if step > 10:
            # start profiling after 10 warmup iterations
            torch.cuda.cudart().cudaProfilerStart()

        nvtx.range_push(f"step_{step}")
        
        # Zero gradients
        if use_optimizer:
            optimizer.zero_grad()
        else:
            model.zero_grad(set_to_none=True)

        # Forward
        with nvtx.range("forward"):
            y = model(x).mean()

        # Backward
        with nvtx.range("backward"):
            y.backward()

        # Optimizer step if enabled
        if use_optimizer:
            with nvtx.range("optimizer_step"):
                #print(f"Step {step}, loss: {y.item():.6f}")
                optimizer.step()
        
        nvtx.range_pop()

def main():
    # Run a larger model if GPU is available
    if torch.cuda.is_available():
        print("Running on GPU")
        run_mlp(dim=4096, num_layers=64, batch_size=1024, num_steps=15, use_optimizer=True)
    else:
        print("Running on CPU")
        run_mlp(dim=128, num_layers=16, batch_size=128, num_steps=15, use_optimizer=True)

if __name__ == "__main__":
    main()
nvtx的作用

代码中的nvtx是NVIDIA提供的NVTX（NVIDIA Tools Extension）库的接口，主要用于在代码中插入标记（markers）或范围（ranges），以便在NVIDIA的性能分析工具（如Nsight Systems、Nsight Compute等）中可视化和分析程序的执行流程与时间分布。

  1. 标记关键操作阶段：
  • 使用nvtx.range("define_model")标记模型定义阶段
  • 使用nvtx.range("define_input")标记输入数据定义阶段
  • 用nvtx.range("forward")和nvtx.range("backward")分别标记前向传播和反向传播阶段
  1. 划分迭代步骤：
  • 通过nvtx.range_push(f"step_{step}")和nvtx.range_pop()标记每个迭代步骤的开始和结束
  1. 性能分析辅助：
  • 这些标记会被NVIDIA的性能分析工具捕获，生成时间线可视化
  • 帮助开发者识别程序中的性能瓶颈，如哪部分操作耗时最长
  • 便于分析不同阶段（如前向/反向传播）的时间占比，优化代码效率
分别在step、layer数量、batch size、dimension上进行线性扩展
python 复制代码 
dim = 256  # @inspect dim
num_layers = 4  # @inspect num_layers 
batch_size = 256  # @inspect batch_size
num_steps = 2  # @inspect num_steps

mlp_base = benchmark("run_mlp", run_mlp(dim=dim, num_layers=num_layers, batch_size=batch_size, num_steps=num_steps)) # @inspect mlp_base


text("Scale the number of steps.")
step_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x num_steps)", 
                     run_mlp(dim=dim, num_layers=num_layers, 
                            batch_size=batch_size, num_steps=scale * num_steps)) # @inspect result, @inspect scale, @inspect num_steps
    step_results.append((scale, result))  # @inspect step_results

text("Scale the number of layers.")
layer_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x num_layers)", 
                     run_mlp(dim=dim, num_layers=scale * num_layers, 
                            batch_size=batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
    layer_results.append((scale, result))  # @inspect layer_results

text("Scale the batch size.")
batch_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x batch_size)", 
                     run_mlp(dim=dim, num_layers=num_layers, 
                            batch_size=scale * batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
    batch_results.append((scale, result))  # @inspect batch_results

text("Scale the dimension.")
dim_results = []
for scale in (2, 3, 4, 5):
    result = benchmark(f"run_mlp({scale}x dim)", 
                     run_mlp(dim=scale * dim, num_layers=num_layers, 
                            batch_size=batch_size, num_steps=num_steps)) # @inspect result, @inspect scale, @inspect num_layers, @inspect num_steps
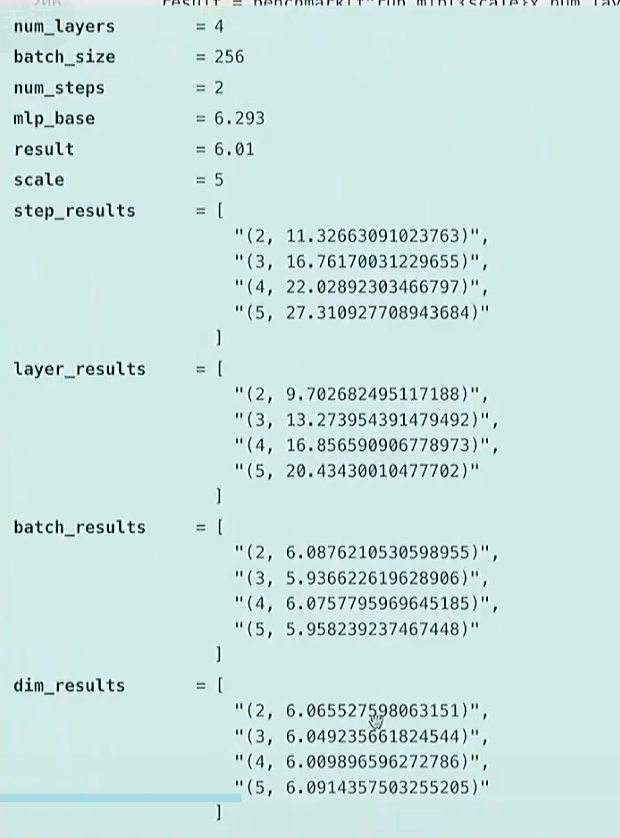
    dim_results.append((scale, result))  # @inspect dim_results

结论 ： step和层数大小，与时间呈线性关系

性能分析-profiler

教程地址：https://docs.pytorch.org/tutorials/recipes/recipes/profiler_recipe.html

python 复制代码 
def profile(description: str, run: Callable, num_warmups: int = 1, with_stack: bool = False):
    # Warmup
    for _ in range(num_warmups):
        run()
    if torch.cuda.is_available():
        torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Run the code with the profiler
    with torch.profiler.profile(
            activities=[ProfilerActivity.CPU, ProfilerActivity.CUDA],
            # Output stack trace for visualization
            with_stack=with_stack,
            # Needed to export stack trace for visualization
            experimental_config=torch._C._profiler._ExperimentalConfig(verbose=True)) as prof:
        run()
        if torch.cuda.is_available():
            torch.cuda.synchronize()  # Wait for CUDA threads to finish (important!)

    # Print out table
    table = prof.key_averages().table(sort_by="cuda_time_total",
                                      max_name_column_width=80,
                                      row_limit=10)
    #text(f"## {description}")
    #text(table, verbatim=True)

    # Write stack trace visualization
    if with_stack:
        text_path = f"var/stacks_{description}.txt"
        svg_path = f"var/stacks_{description}.svg"
        prof.export_stacks(text_path, "self_cuda_time_total")

    return table

add

matmul

matmul(dim=128)

cdist

gelu

softmax

python 复制代码 
def pytorch_softmax(x: torch.Tensor):
    return torch.nn.functional.softmax(x, dim=-1)

内核融合的思想

可以参考【cs336学习笔记】[第5课]详解GPU架构，性能优化

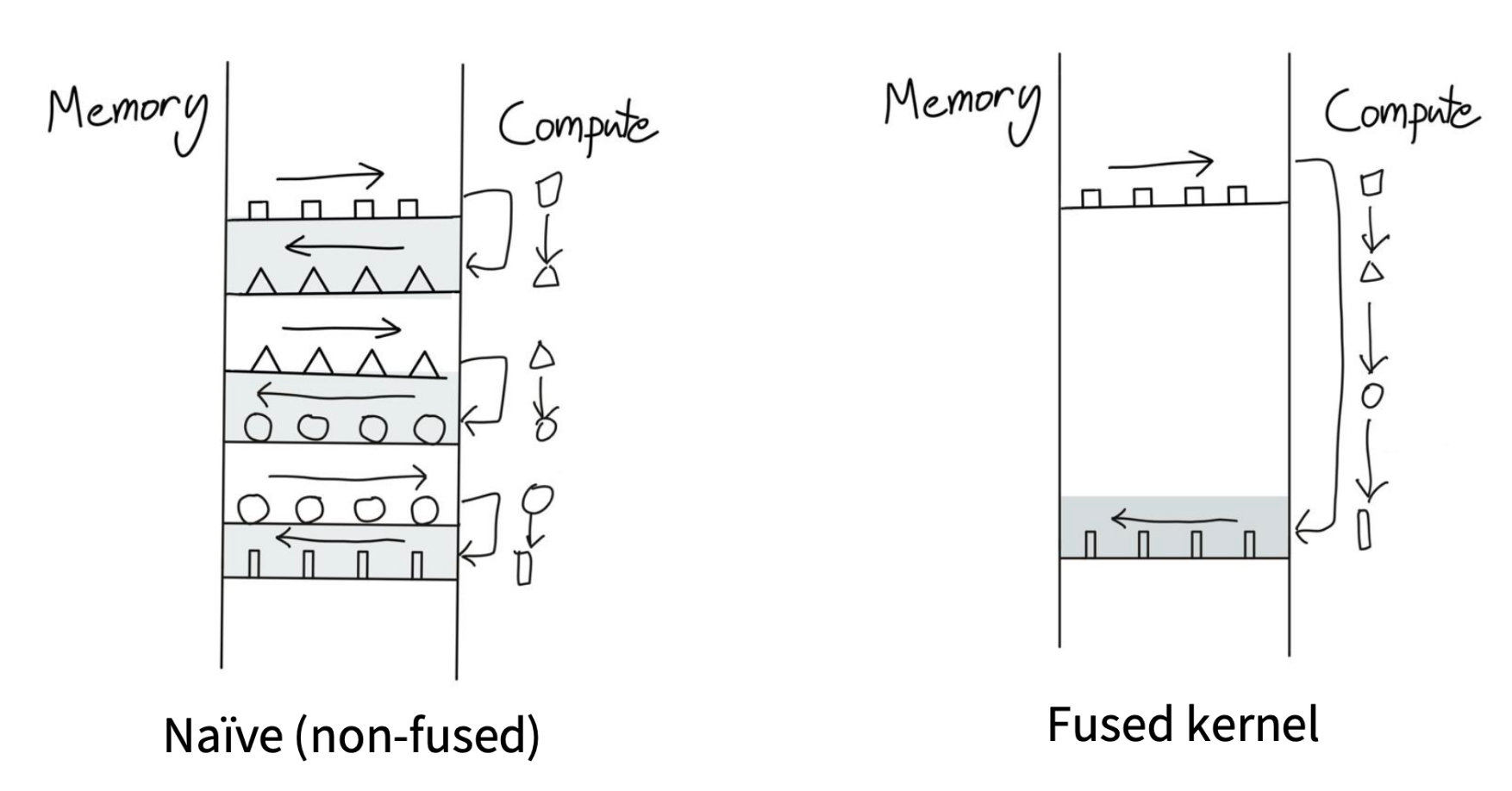
不同版本的GELU实现方式

1.pytorch版 vs 手动实现版

pytorch官方实现：https://docs.pytorch.org/docs/stable/generated/torch.nn.GELU.html

python 复制代码 
def pytorch_gelu(x: torch.Tensor):
    # Use the tanh approximation to match our implementation
    return torch.nn.functional.gelu(x, approximate="tanh")
python 复制代码 
def manual_gelu(x: torch.Tensor):
    return 0.5 * x * (1 + torch.tanh(0.79788456 * (x + 0.044715 * x * x * x)))


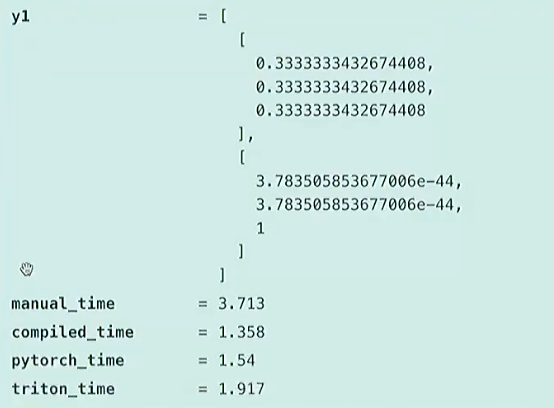
结论：

  • y1和y2的值相等，但是运行时间上差了8倍

  • manual_gelu是很朴素的思想，一步一步操作，有大量算子参与运算，例如BinaryFunctor<f...调用了三次cuda kernel

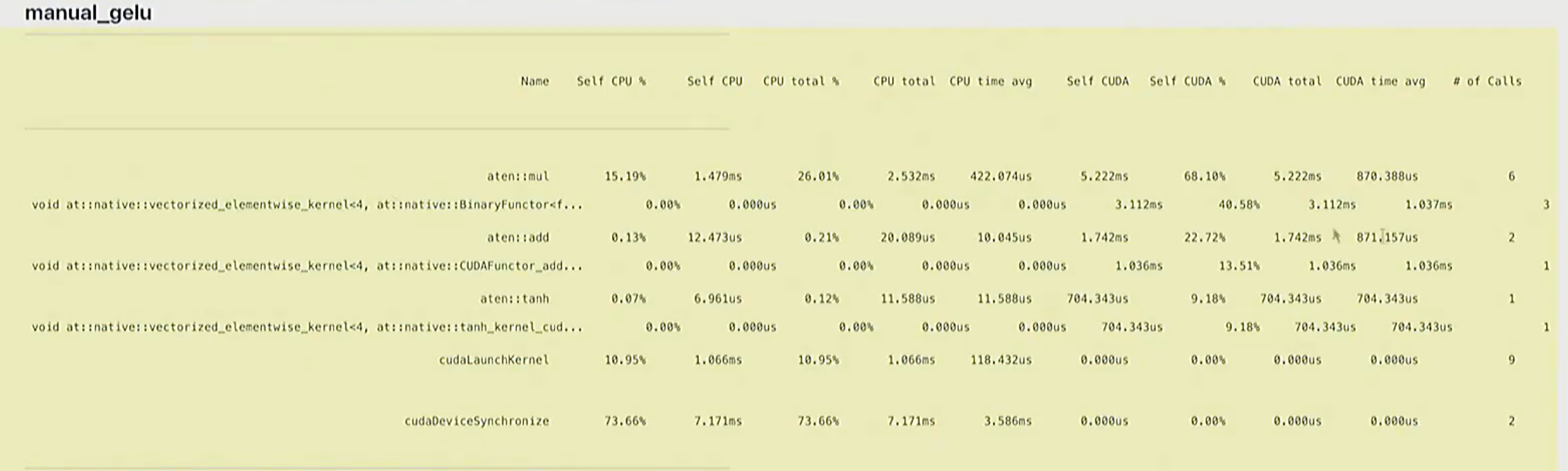
  • pytorch是算子融合后的版本，只调用了一次cuda kernel

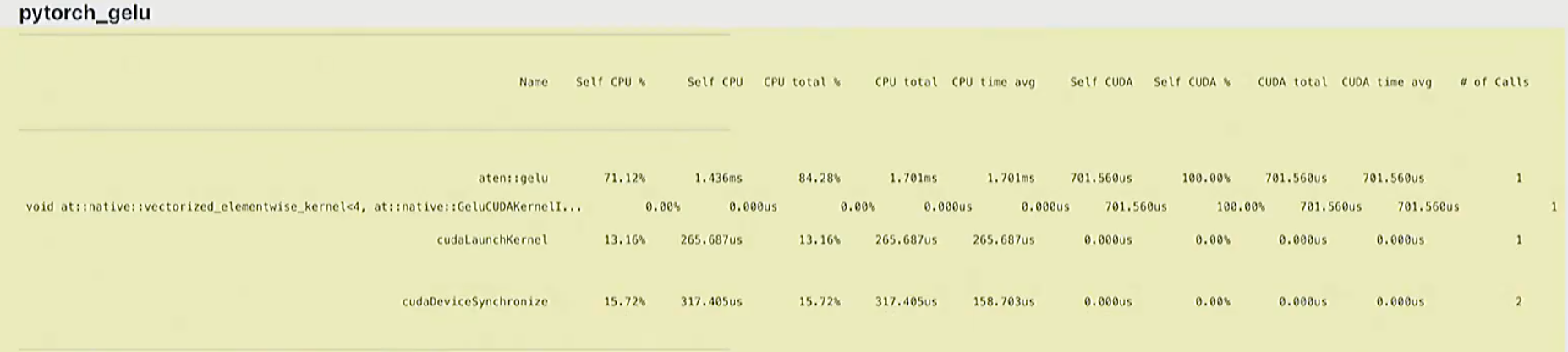
2. cuda实现GELU

step1. C++实现的gelu函数，文件名：gelu.cu
c 复制代码 
#include <math.h>               // 包含标准数学函数（如tanh）
#include <torch/extension.h>    // PyTorch扩展开发必备头文件，提供张量操作等接口
#include <c10/cuda/CUDAException.h>  // CUDA错误处理工具

/**
 * CUDA核函数：计算GELU激活函数
 * 每个线程处理输入张量中的一个元素
 * 
 * @param in 输入张量的数据指针（GPU内存）
 * @param out 输出张量的数据指针（GPU内存）
 * @param num_elements 张量中元素的总数量
 */
__global__ void gelu_kernel(float* in, float* out, int num_elements) {
    // 计算当前线程负责处理的元素索引
    // blockIdx.x: 当前线程块在网格中的索引
    // blockDim.x: 每个线程块中包含的线程数
    // threadIdx.x: 当前线程在线程块中的索引
    int i = blockIdx.x * blockDim.x + threadIdx.x;

    // 边界检查：确保线程只处理有效范围内的元素
    // 当总元素数不是线程块大小的整数倍时，避免越界访问
    if (i < num_elements) {  
        // GELU激活函数计算公式（近似实现）
        // 原始公式：GELU(x) = 0.5 * x * (1 + erf(x / sqrt(2)))
        // 这里使用等价近似：0.5 * x * (1 + tanh(sqrt(2/π) * (x + 0.044715 * x^3)))
        // 其中0.79788456是sqrt(2/π)的近似值
        out[i] = 0.5 * in[i] * (1.0 + tanh(0.79788456 * (in[i] + 0.044715 * in[i] * in[i] * in[i])));
    }
}

/**
 * 辅助函数：计算整数除法的向上取整
 * 用于确定处理所有元素所需的线程块数量
 * 
 * @param a 被除数（通常是元素总数）
 * @param b 除数（通常是每个线程块的线程数）
 * @return 向上取整的结果（ceil(a / b)）
 */
inline unsigned int cdiv(unsigned int a, unsigned int b) {
    // 整数除法向上取整的经典实现
    // 例如：cdiv(5, 2) = 3，cdiv(4, 2) = 2
    return (a + b - 1) / b;
}

/**
 * PyTorch接口函数：对输入张量应用GELU激活函数
 * 这是Python代码调用的入口点
 * 
 * @param x 输入张量（必须是CUDA设备上的连续张量）
 * @return 应用GELU后的输出张量
 */
torch::Tensor gelu(torch::Tensor x) {
    // 输入验证：确保张量在CUDA设备上
    TORCH_CHECK(x.device().is_cuda(), "输入张量必须在CUDA设备上");
    // 输入验证：确保张量是连续内存布局（避免非连续内存导致的访问效率问题）
    TORCH_CHECK(x.is_contiguous(), "输入张量必须是连续的（contiguous）");

    // 创建与输入张量形状、类型、设备相同的空张量作为输出
    torch::Tensor y = torch::empty_like(x);

    // 计算输入张量的总元素数量
    int num_elements = x.numel();
    // 定义每个线程块的线程数量（1024是CUDA中常用的线程块大小，适合大多数GPU）
    int block_size = 1024;
    // 计算需要的线程块数量（向上取整确保所有元素都被处理）
    int num_blocks = cdiv(num_elements, block_size);

    // 启动CUDA核函数
    // <<<num_blocks, block_size>>> 是CUDA的核函数启动配置语法
    // 第一个参数：网格中的线程块数量
    // 第二个参数：每个线程块中的线程数量
    gelu_kernel<<<num_blocks, block_size>>>(
        x.data_ptr<float>(),  // 输入张量的数据指针（GPU）
        y.data_ptr<float>(),  // 输出张量的数据指针（GPU）
        num_elements          // 总元素数量
    );
    // 检查核函数启动是否成功，若失败会抛出异常
    C10_CUDA_KERNEL_LAUNCH_CHECK();

    // 返回计算结果
    return y;
}
step2. 编译并加载CUDA实现的GELU激活函数
python 复制代码 
def create_cuda_gelu():
    """
    编译并加载CUDA实现的GELU激活函数，返回可在Python中调用的函数
    
    返回:
        编译好的CUDA GELU函数，如果CUDA不可用则返回None
    """
    # 设置环境变量，启用CUDA阻塞式启动模式
    # 这会让CUDA操作同步执行，便于调试（但可能降低性能）
    os.environ["CUDA_LAUNCH_BLOCKING"] = "1"

    # 读取CUDA源代码文件（包含GELU的核心实现）
    cuda_gelu_src = open("gelu.cu").read()
    # 打印CUDA源代码（verbatim=True确保原样输出，不进行转义）
    text(cuda_gelu_src, verbatim=True)

    # C++源代码：声明GELU函数接口
    # 这是连接Python和CUDA实现的桥梁
    cpp_gelu_src = "torch::Tensor gelu(torch::Tensor x);"

    # 打印说明信息：编译CUDA代码并绑定到Python模块
    text("Compile the CUDA code and bind it to a Python module.")
    
    # 确保编译目录存在，避免因目录不存在导致编译失败
    ensure_directory_exists("var/cuda_gelu")
    
    # 检查CUDA是否可用，不可用则返回None
    if not torch.cuda.is_available():
        return None
    
    # 编译并加载CUDA和C++代码，创建Python可调用的模块
    module = load_inline(
        cuda_sources=[cuda_gelu_src],  # CUDA源代码列表
        cpp_sources=[cpp_gelu_src],    # C++源代码列表
        functions=["gelu"],            # 需要从模块中导出的函数名
        extra_cflags=["-O2"],          # 额外的编译标志（-O2表示开启优化）
        verbose=True,                  # 编译过程中输出详细信息
        name="inline_gelu",            # 模块名称
        build_directory="var/cuda_gelu",  # 编译输出目录
    )

    # 从编译好的模块中获取gelu函数
    cuda_gelu = getattr(module, "gelu")
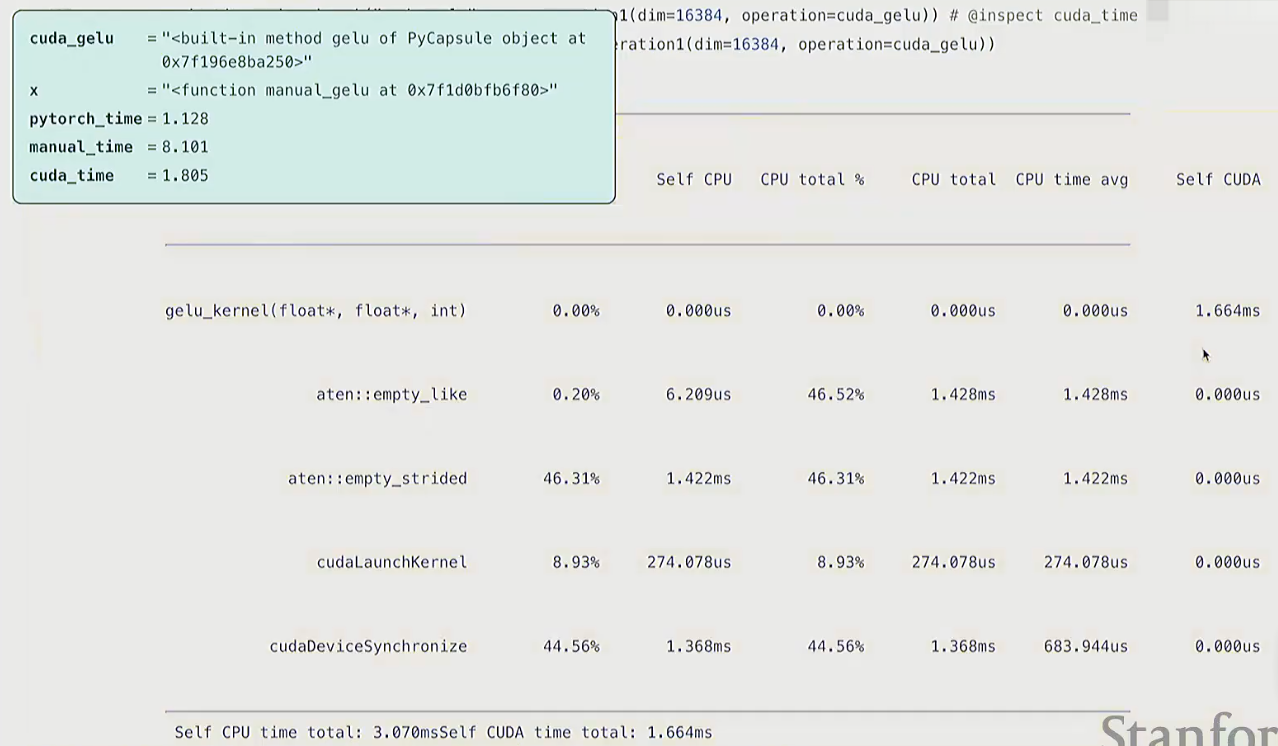
    return cuda_gelu
结论
  • cuda实现的gelu运行时间相比于mamual有很大提升

Q：为什么manual的实现这么慢？

A：

  • 并不是因为它把数据从GPU发回CPU的通信成本导致的（比如x驻留在GPU上，我们在GPU分配它，虽然我们会写as device=cuda，但其实数据不会一直驻留在SM上）。
  • 而是，例如在计算x的平方时, 乘法操作会把向量从全局内存读到SMs中, 进行计算, 再写回去。所以这涉及到的是，DRAM与SMs的通信成本, 而非CPU到GPU的通信成本。
  • 如果写成as device=cpu, 就会产生CPU传输成本, 再加上DRAM传输成本。

Triton

Triton vs Cuda

特性 CUDA Triton
Memory coalescing (transfer from DRAM) 内存合并（从DRAM传输数据） manual（手动） automatic（自动）
Shared memory management 共享内存管理 manual（手动） automatic（自动）
Scheduling within SMs 流式多处理器（SM）内调度 manual（手动） automatic（自动）
Scheduling across SMs 流式多处理器（SM）间调度 manual（手动） manual（手动）

补充说明：

  • 内存合并（Memory Coalescing）：GPU访问DRAM时的一种优化技术，通过让线程束（warp）内的线程访问连续内存地址，减少内存请求次数，提升数据传输效率。CUDA需开发者手动确保内存访问模式符合合并规则，Triton会自动优化该过程。
  • 共享内存（Shared Memory）：GPU片上高速内存，访问速度远快于DRAM，常用于线程块内数据复用。CUDA需手动分配、读写和释放共享内存，Triton会根据代码逻辑自动管理。
  • 流式多处理器（SM）：GPU的核心计算单元（如NVIDIA GPU的SM、AMD GPU的CU），一个GPU包含多个SM。"SM内调度"指同一SM内线程/线程块的执行顺序优化，"SM间调度"指不同SM间的任务分配，后者因涉及GPU硬件资源全局分配，目前CUDA和Triton均需手动干预（或依赖框架高层调度）。

triton的gelu实现

python 复制代码 
@triton.jit
def triton_gelu_kernel(x_ptr, y_ptr, num_elements, BLOCK_SIZE: tl.constexpr):
    """
    Triton核函数：实现GELU激活函数的并行计算
    由triton.jit装饰器编译为高效GPU代码，自动优化内存访问和线程调度
    
    参数:
        x_ptr: 输入张量的数据指针（GPU内存）
        y_ptr: 输出张量的数据指针（GPU内存）
        num_elements: 输入张量的总元素数量
        BLOCK_SIZE: 每个线程块处理的元素数量（编译期常量）
    """
    # 输入数据位于x_ptr，输出结果将存储在y_ptr
    # 线程块划分示意图：
    #     |        Block 0            |          Block 1          |      ...      |
    #                            BLOCK_SIZE                                 num_elements

    # 获取当前线程块在网格中的ID（轴0方向，1D网格）
    pid = tl.program_id(axis=0)
    # 计算当前线程块处理的第一个元素索引
    block_start = pid * BLOCK_SIZE

    # 生成当前线程块内所有线程要处理的元素偏移量
    # 例如：block_start=1024, BLOCK_SIZE=1024时，offsets为[1024, 1025, ..., 2047]
    offsets = block_start + tl.arange(0, BLOCK_SIZE)

    # 创建掩码：标记哪些偏移量在有效元素范围内（处理总元素数不是BLOCK_SIZE整数倍的情况）
    mask = offsets < num_elements

    # 从全局内存加载数据到线程块寄存器
    # mask确保只加载有效元素，避免越界访问
    x = tl.load(x_ptr + offsets, mask=mask)

    # 计算GELU激活函数（近似实现）
    # 公式：GELU(x) = 0.5 * x * (1 + tanh(sqrt(2/π) * (x + 0.044715 * x³)))
    # 其中0.79788456是sqrt(2/π)的近似值
    
    # 计算tanh内部的表达式
    a = 0.79788456 * (x + 0.044715 * x * x * x)
    # Triton原生不直接提供tanh函数，使用等价公式：tanh(a) = (e^(2a) - 1) / (e^(2a) + 1)
    exp = tl.exp(2 * a)
    tanh = (exp - 1) / (exp + 1)
    # 计算最终GELU结果
    y = 0.5 * x * (1 + tanh)

    # 将计算结果从寄存器存储到全局内存的输出地址
    # mask确保只存储有效元素的结果
    tl.store(y_ptr + offsets, y, mask=mask)
    
def triton_gelu(x: torch.Tensor):
    """
    使用Triton框架实现的GELU激活函数，在GPU上高效执行
    
    参数:
        x: 输入张量，必须是CUDA设备上的连续张量
    返回:
        应用GELU激活函数后的输出张量，形状与输入相同
    """
    # 输入验证：确保张量在CUDA设备上（Triton kernels仅在GPU上运行）
    assert x.is_cuda
    # 输入验证：确保张量是连续内存布局（优化内存访问效率）
    assert x.is_contiguous()

    # 分配与输入形状、类型、设备相同的空张量作为输出
    y = torch.empty_like(x)

    # 确定并行计算的网格划分方式
    # 获取输入张量的总元素数量
    num_elements = x.numel()
    # 每个线程块处理的元素数量（Triton中通常设为1024，适配GPU warp大小）
    block_size = 1024
    # 计算需要的线程块数量（向上取整确保所有元素都被处理）
    num_blocks = triton.cdiv(num_elements, block_size)

    # 启动Triton kernel执行GELU计算
    # [(num_blocks,)] 定义网格维度（此处为1D网格）
    # 传递输入张量x、输出张量y、元素总数和块大小参数
    triton_gelu_kernel[(num_blocks,)](x, y, num_elements, BLOCK_SIZE=block_size)

    # 返回计算结果
    return y

PTX

不同版本的gelu对比

python 复制代码 
# 直接利用torch.compile
compiled_gelu = torch.compile(manual_gelu)

torch.compile 将未经优化的代码，转为更优化的代码，会尝试自动融合算子。可以看到，底层用的是triton

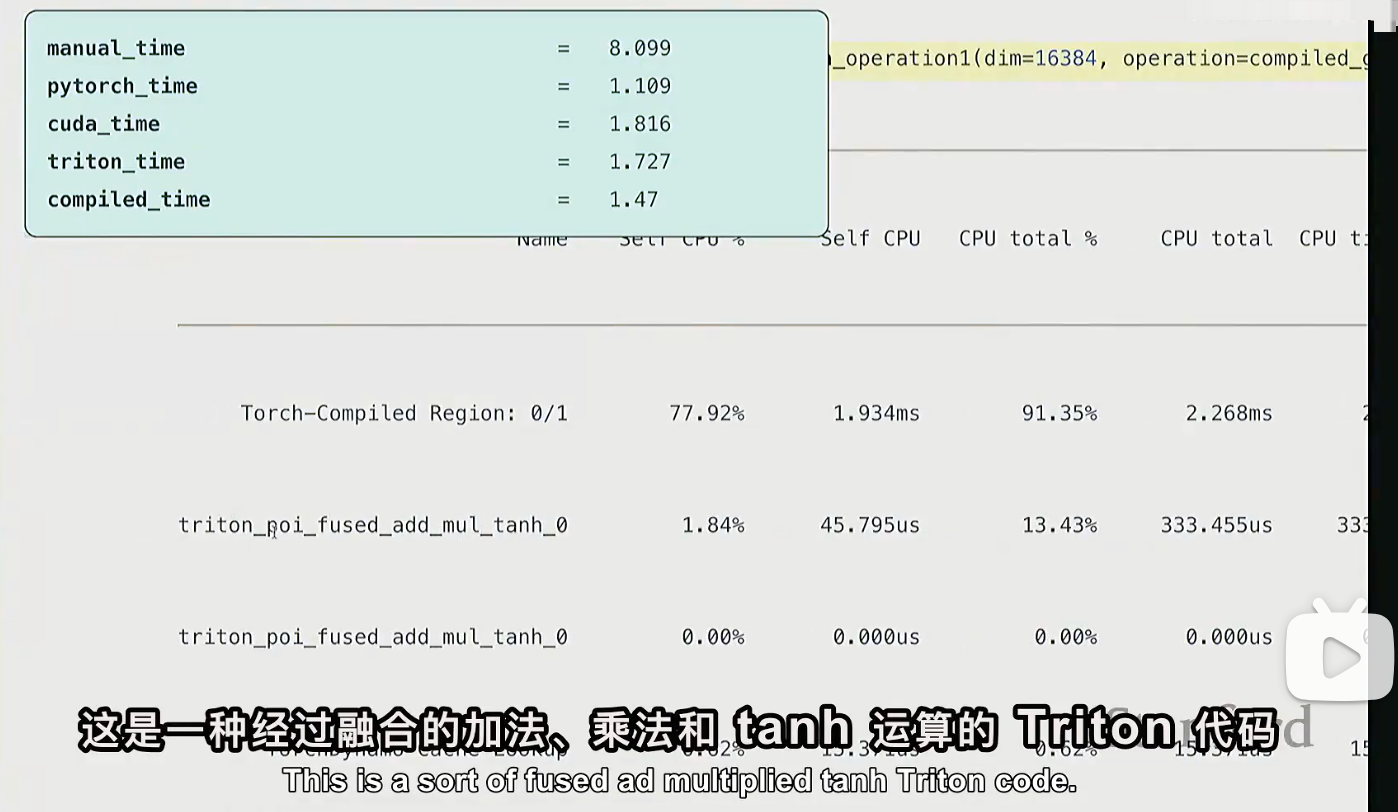
不同版本的softmax

manual

python 复制代码 
def manual_softmax(x: torch.Tensor):
    """
    手动实现Softmax激活函数，对输入张量的每一行进行归一化处理
    Softmax公式：softmax(x)_ij = exp(x_ij) / sum(exp(x_ik) for k in 0..N-1)
    
    参数:
        x: 输入张量，形状为[M, N]，M为样本数，N为特征数
    返回:
        y: 经过Softmax处理的张量，形状与输入相同，每行元素和为1
    """
    # 获取输入张量的形状：M为行数（样本数），N为列数（特征数）
    M, N = x.shape

    # 计算每一行的最大值（用于数值稳定性，防止指数溢出）
    # 操作：MN次读取（遍历所有元素），M次写入（存储每行最大值）
    x_max = x.max(dim=1)[0]  # [0]表示取最大值结果，忽略索引

    # 每行元素减去该行的最大值（数值稳定化步骤）
    # 操作：MN次读取（x的所有元素） + M次读取（x_max的所有元素），MN次写入（存储结果）
    # [:, None]将x_max从形状[M]扩展为[M, 1]，以便与x进行广播运算
    x = x - x_max[:, None]

    # 对处理后的元素进行指数运算（计算分子）
    # 操作：MN次读取（x的所有元素），MN次写入（存储指数结果）
    numerator = torch.exp(x)

    # 计算每行的指数和（归一化常数，即分母）
    # 操作：MN次读取（numerator的所有元素），M次写入（存储每行的和）
    denominator = numerator.sum(dim=1)

    # 计算最终的Softmax结果：分子除以分母（带广播）
    # 操作：MN次读取（numerator） + M次读取（denominator），MN次写入（存储结果）
    y = numerator / denominator[:, None]

    # 内存操作统计：
    # 总读取次数：5MN + M（上述各步骤读取次数之和）
    # 总写入次数：3MN + 2M（上述各步骤写入次数之和）
    # 理论优化空间：理想情况下只需MN次读取和MN次写入（可实现4倍速提升）
    return y

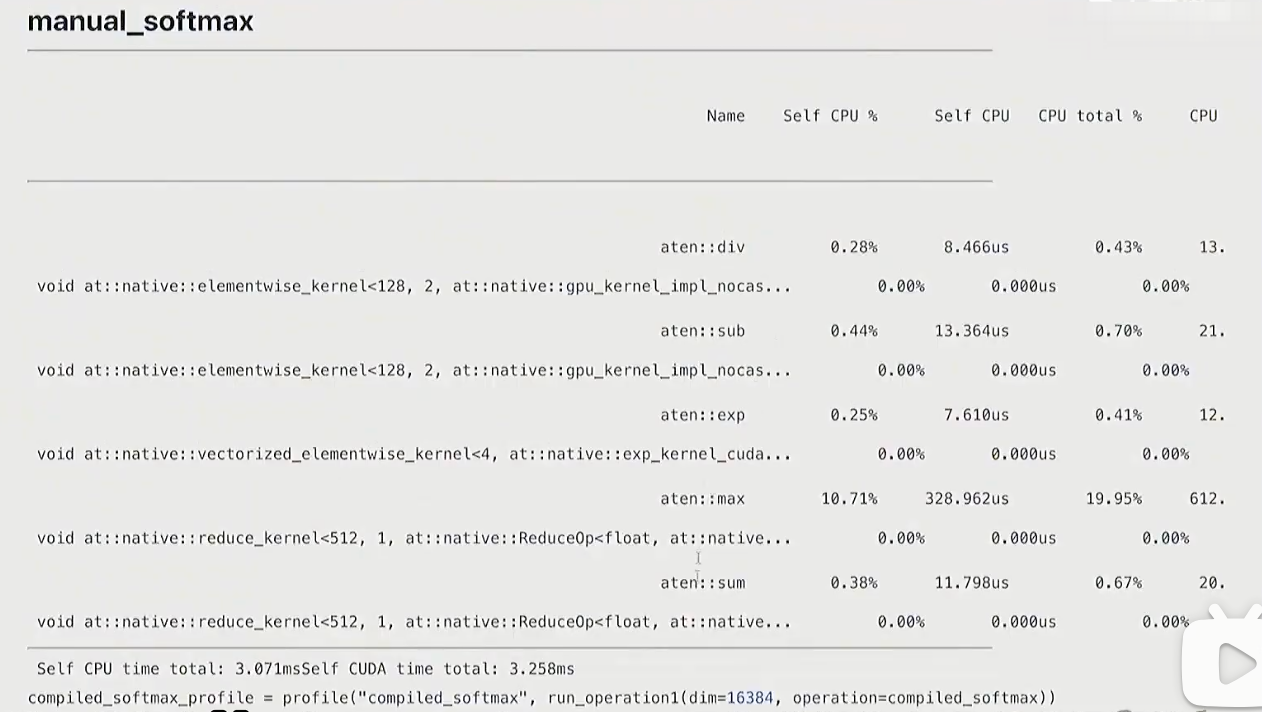
triton

python 复制代码 
def triton_softmax(x: torch.Tensor):
    """
    使用Triton框架优化的Softmax实现，通过GPU并行计算提升性能
    
    参数:
        x: 输入张量，形状为[M, N]，需为CUDA设备上的连续张量
    返回:
        y: 归一化后的张量，形状与输入相同
    """
    # 分配与输入形状、类型、设备相同的空张量作为输出
    y = torch.empty_like(x)

    # 确定并行计算的网格配置
    M, N = x.shape                          # M为行数，N为列数
    # 每个线程块处理一行，块大小设为大于等于列数的最小2的幂（优化内存访问）
    block_size = triton.next_power_of_2(N)
    num_blocks = M                          # 行数决定线程块数量（每个线程块处理一行）

    # 启动Triton核函数执行并行计算
    triton_softmax_kernel[(M,)](            # 网格维度：M个线程块（每行一个）
        x_ptr=x, y_ptr=y,                   # 输入输出张量指针
        x_row_stride=x.stride(0),           # 输入张量行间距（每行第一个元素的内存偏移）
        y_row_stride=y.stride(0),           # 输出张量行间距
        num_cols=N,                         # 列数（特征维度）
        BLOCK_SIZE=block_size               # 线程块大小（编译期常量）
    )

    return y


@triton.jit
def triton_softmax_kernel(x_ptr, y_ptr, x_row_stride, y_row_stride, num_cols, BLOCK_SIZE: tl.constexpr):
    """
    Triton核函数：并行计算Softmax，每个线程块处理输入张量的一行
    
    参数:
        x_ptr: 输入张量的数据指针（GPU内存）
        y_ptr: 输出张量的数据指针（GPU内存）
        x_row_stride: 输入张量每行的内存步长（字节数）
        y_row_stride: 输出张量每行的内存步长（字节数）
        num_cols: 每行的元素数量（特征维度）
        BLOCK_SIZE: 线程块大小（编译期常量，需>=num_cols）
    """
    # 确保线程块大小足够容纳一行的所有元素
    assert num_cols <= BLOCK_SIZE

    # 每个线程块独立处理一行，获取当前处理的行索引
    row_idx = tl.program_id(0)
    # 生成当前线程块内所有线程的列偏移量（0到BLOCK_SIZE-1）
    col_offsets = tl.arange(0, BLOCK_SIZE)

    # 计算输入张量中当前行的起始内存地址
    x_start_ptr = x_ptr + row_idx * x_row_stride
    # 计算当前行所有元素的内存地址（带列偏移）
    x_ptrs = x_start_ptr + col_offsets
    # 从全局内存加载一行数据，超出有效列数的位置用-inf填充（不影响max计算）
    # mask确保只加载有效列元素，避免越界访问
    x_row = tl.load(x_ptrs, mask=col_offsets < num_cols, other=float("-inf"))

    # 并行计算Softmax（所有操作在寄存器中完成，减少全局内存访问）
    # 1. 减去行内最大值（数值稳定化）
    x_row = x_row - tl.max(x_row, axis=0)
    # 2. 计算指数（分子）
    numerator = tl.exp(x_row)
    # 3. 计算归一化常数（分母）
    denominator = tl.sum(numerator, axis=0)
    # 4. 计算最终结果
    y_row = numerator / denominator

    # 计算输出张量中当前行的起始内存地址
    y_start_ptr = y_ptr + row_idx * y_row_stride
    # 计算当前行所有输出元素的内存地址（带列偏移）
    y_ptrs = y_start_ptr + col_offsets
    # 将计算结果存储到全局内存，只存储有效列元素
    tl.store(y_ptrs, y_row, mask=col_offsets < num_cols)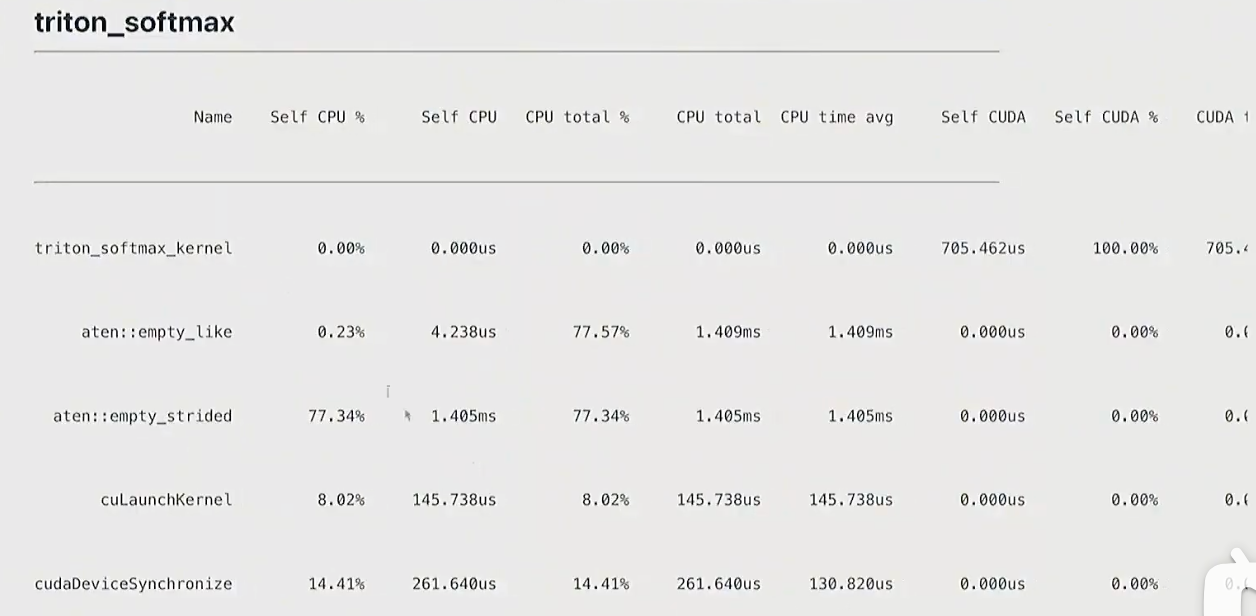

torch.compile

python 复制代码 
compiled_softmax = torch.compile(manual_softmax)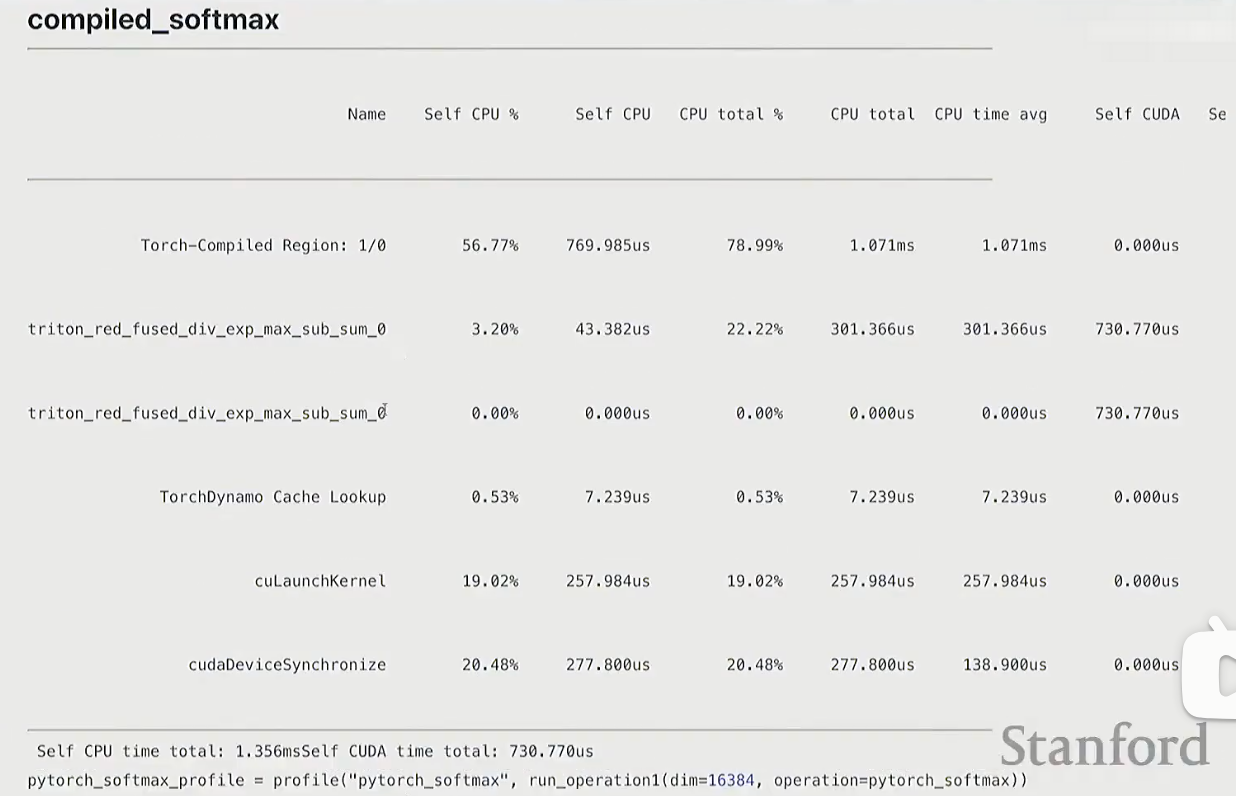

pytorch

python 复制代码 
def pytorch_softmax(x: torch.Tensor):
    return torch.nn.functional.softmax(x, dim=-1)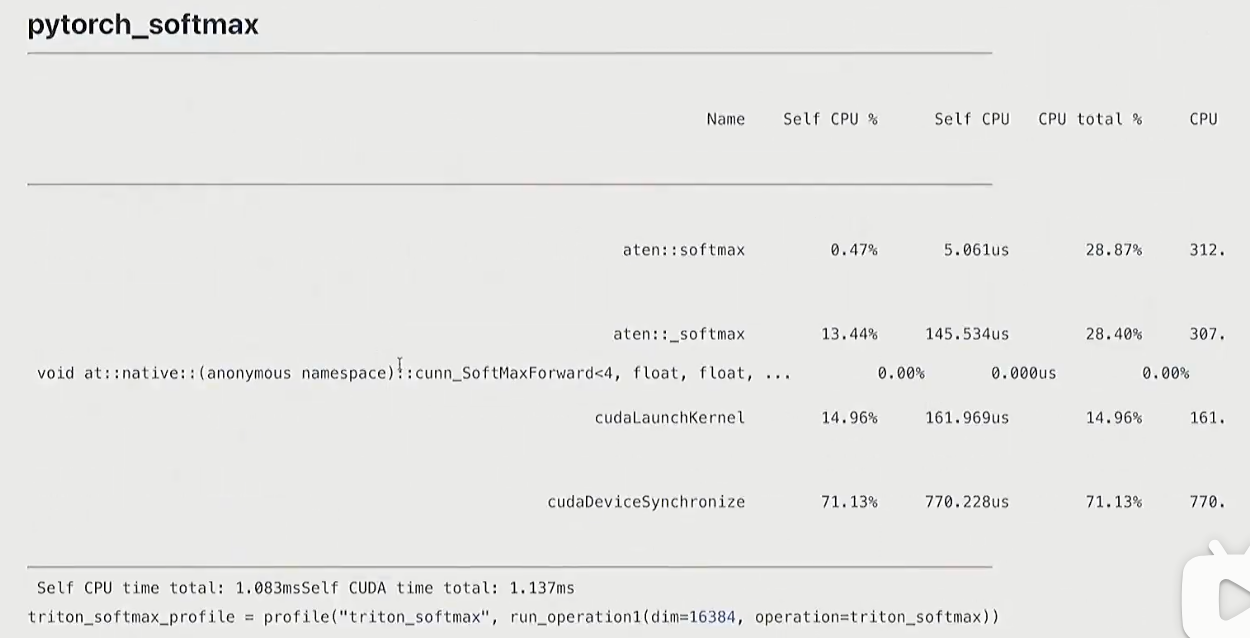

结论

  • torch.compile会比pytorch实现更好
  • mamual调用cuda的次数最多
相关推荐
山烛3 小时前
深度学习：CUDA、PyTorch下载安装
人工智能·pytorch·python·深度学习·cuda
深瞳智检4 小时前
目标检测数据集 第007期-基于yolo标注格式的茶叶病害检测数据集(含免费分享)
人工智能·深度学习·yolo·目标检测·计算机视觉
CoovallyAIHub7 小时前
目标检测模型评估金标准：mAP全解读，Coovally助你高效调参！
深度学习·算法·计算机视觉
CoovallyAIHub7 小时前
基于视觉的果园无人机导航：一种基于干预模仿学习与VAE控制器的真实世界验证
深度学习·算法·计算机视觉
小饼干超人8 小时前
详解triton.jit及PTX
人工智能·大模型·推理加速
、水水水水水9 小时前
RAG学习（五）——查询构建、Text2SQL、查询重构与分发
人工智能·python·深度学习·nlp
瑶光守护者9 小时前
【卫星通信】超低码率语音编码ULBC：EnCodec神经音频编解码器架构深度解析
深度学习·音视频·卫星通信·语音编解码·ulbc
JolyouLu12 小时前
LangChain4J-基础(整合Spring、RAG、MCP、向量数据库、提示词、流式输出)
大模型·提示词·向量数据库·rag·mcp·langchain4j
dundunmm13 小时前
【每天一个知识点】训推一体机
人工智能·大模型·硬件·软件·训练·推理
热门推荐
01UV安装并设置国内源02KGG转MP3工具|非KGM文件|解密音频03Cursor 快速入门指南：从安装到核心功能04【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）05【踩坑笔记】50系显卡适配的 PyTorch 安装0620个国内外主流AI绘画工具大汇总（最新免费可用~）07Claude Code VSCode集成开发指南：AI编程助手完整配置08蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接09突破百度网盘的下载限速，两种方法教会你【超详细】10UnityHub Validation Failed下载编辑器错误，添加模块报错的解决方案