这两段MATLAB代码(BABJ.m 和 CNN_GRUQSTB.m)分别完成数据预处理与缺失值标识和基于CNN-GRU混合神经网络的缺失值预测填补任务。以下是详细分析:
一、主要功能
- BABJ.m
• 功能:从多个Excel文件中读取数据,匹配并合并多个数据源。
• 输出:标识出 Y 表中四个变量的缺失值位置,并打印缺失值。 - CNN_GRUQSTB.m
• 功能:使用CNN-GRU混合神经网络模型对 Y 表中"变量1"的缺失值进行预测填补。
• 输入:使用 BABJ.m 中标识的缺失值位置划分训练集和测试集。
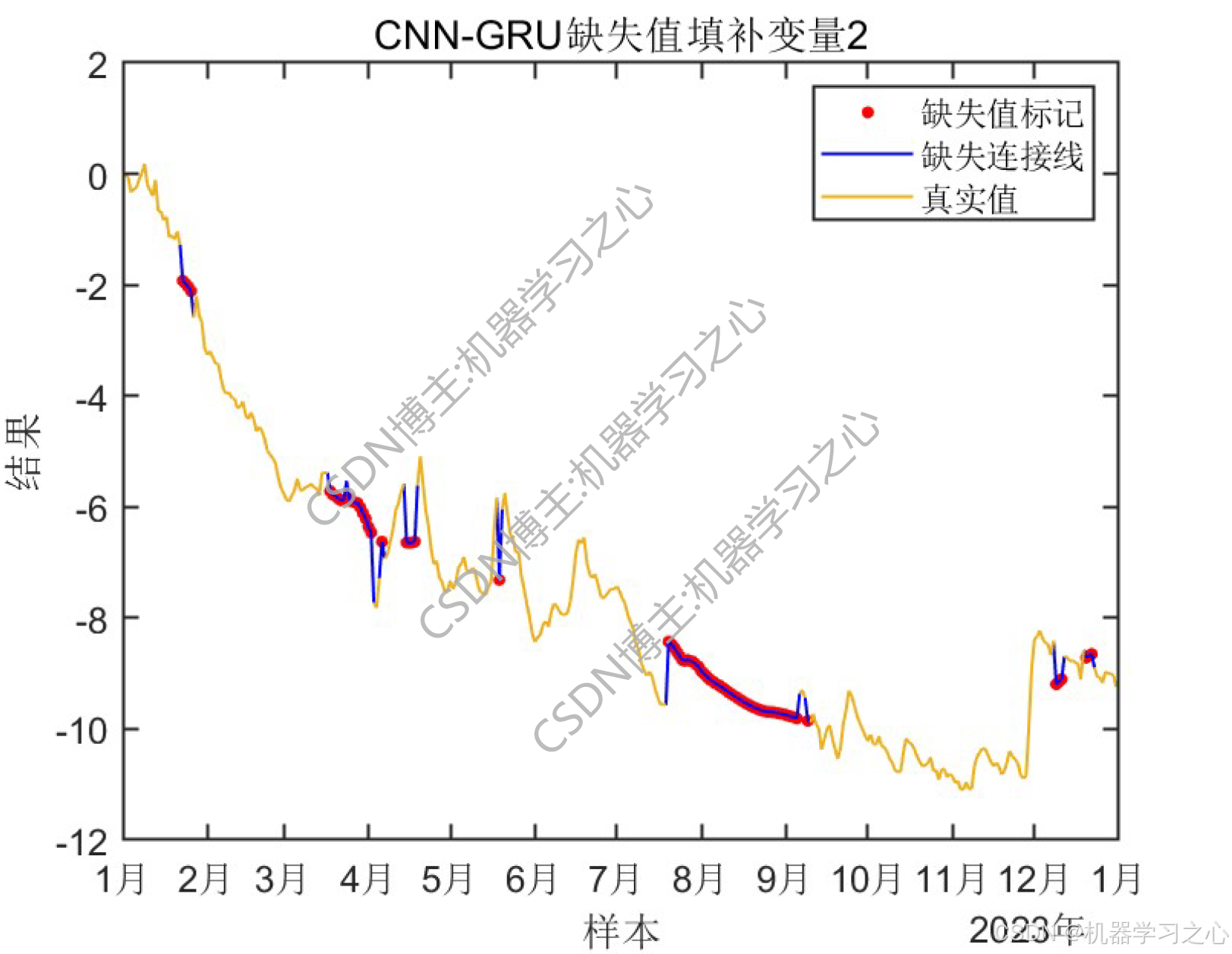
• 输出:预测缺失值、保存结果、绘制填补效果图。
二、逻辑关联
• BABJ.m 输出缺失值索引,CNN_GRUQSTB.m 使用该索引划分训练集和测试集。
• BABJ.m 负责数据清洗与缺失值标识,CNN_GRUQSTB.m 负责建模预测与可视化。
三、算法步骤与技术路线
BABJ.m:
-
读取多个Excel文件。
-
填充 Y 中的四个变量。
-
检查并输出每个变量的缺失值位置。
CNN_GRUQSTB.m:
-
数据划分:根据 missingIdx1 将数据分为训练集和测试集。
-
数据预处理:归一化、平铺、转换为序列格式。
-
构建CNN-GRU模型:
• 输入层 → 序列折叠 → 卷积层(CNN)→ GRU层 → 全连接层 → 回归输出。
-
训练模型:使用Adam优化器,设置学习率下降策略。
-
预测与反归一化:对缺失值进行预测并还原到原始尺度。
-
可视化:绘制真实值、预测值和缺失位置标记。
四、公式
1. CNN(卷积神经网络)
卷积操作公式:
y(i)=∑kx(i+k)⋅w(k)+b y(i) = \sum_{k} x(i + k) \cdot w(k) + b y(i)=k∑x(i+k)⋅w(k)+b
其中:
- xxx 是输入信号
- www 是卷积核权重
- bbb 是偏置项
- y(i)y(i)y(i) 是位置 iii 的输出
2. GRU(门控循环单元)
更新门:
zt=σ(Wz⋅[ht−1,xt]) z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) zt=σ(Wz⋅[ht−1,xt])
重置门:
rt=σ(Wr⋅[ht−1,xt]) r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) rt=σ(Wr⋅[ht−1,xt])
候选隐藏状态:
h~t=tanh(W⋅[rt⊙ht−1,xt]) \tilde{h}t = \tanh(W \cdot [r_t \odot h{t-1}, x_t]) h~t=tanh(W⋅[rt⊙ht−1,xt])
最终隐藏状态:
ht=(1−zt)⊙ht−1+zt⊙h~t h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t ht=(1−zt)⊙ht−1+zt⊙h~t
其中:
- σ\sigmaσ 是sigmoid激活函数
- ⊙\odot⊙ 表示逐元素乘法
- ht−1h_{t-1}ht−1 是上一时间步的隐藏状态
- xtx_txt 是当前时间步的输入
- WzW_zWz, WrW_rWr, WWW 是权重矩阵
3. 归一化(mapminmax)
最小-最大归一化公式:
xnorm=x−min(x)max(x)−min(x) x_{\text{norm}} = \frac{x - \min(x)}{\max(x) - \min(x)} xnorm=max(x)−min(x)x−min(x)
其中:
- xxx 是原始数据
- min(x)\min(x)min(x) 和 max(x)\max(x)max(x) 分别是数据的最小值和最大值
- xnormx_{\text{norm}}xnorm 是归一化后的数据,范围在[0, 1]之间
4. 反归一化
最小-最大反归一化公式:
xoriginal=xnorm⋅(max(x)−min(x))+min(x) x_{\text{original}} = x_{\text{norm}} \cdot (\max(x) - \min(x)) + \min(x) xoriginal=xnorm⋅(max(x)−min(x))+min(x)
其中:
- xnormx_{\text{norm}}xnorm 是归一化后的数据
- min(x)\min(x)min(x) 和 max(x)\max(x)max(x) 是原始数据的最小值和最大值
- xoriginalx_{\text{original}}xoriginal 是还原到原始尺度的数据
5. Adam优化器更新规则
一阶矩估计:
mt=β1⋅mt−1+(1−β1)⋅gt m_t = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot g_t mt=β1⋅mt−1+(1−β1)⋅gt
二阶矩估计:
vt=β2⋅vt−1+(1−β2)⋅gt2 v_t = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot g_t^2 vt=β2⋅vt−1+(1−β2)⋅gt2
偏差修正:
m^t=mt1−β1t \hat{m}_t = \frac{m_t}{1 - \beta_1^t} m^t=1−β1tmt
v^t=vt1−β2t \hat{v}_t = \frac{v_t}{1 - \beta_2^t} v^t=1−β2tvt
参数更新:
θt=θt−1−α⋅m^tv^t+ϵ \theta_t = \theta_{t-1} - \alpha \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} θt=θt−1−α⋅v^t +ϵm^t
其中:
- gtg_tgt 是当前时间步的梯度
- β1\beta_1β1, β2\beta_2β2 是动量参数(通常设为0.9和0.999)
- α\alphaα 是学习率
- ϵ\epsilonϵ 是小常数(通常为10−810^{-8}10−8)用于数值稳定性
这些公式共同构成了CNN-GRU混合神经网络模型的理论基础,用于处理序列数据中的缺失值填补问题。
五、参数设定
模型结构:
• 卷积核:3×1,特征图数:16 → 32
• GRU隐藏单元数:64
• 输出层:全连接层 + 回归层
训练参数:
• 优化器:Adam
• 最大训练轮数:100
• 批大小:64
• 初始学习率:0.001
• L2正则化系数:0.001
• 学习率每50轮下降为原来的0.1倍
六、运行环境
• 软件:MATLAB(建议R2020b及以上版本,支持Deep Learning Toolbox)
• 依赖工具箱:
• Deep Learning Toolbox
• Statistics and Machine Learning Toolbox
• 数据格式:Excel文件(.xlsx)