在机器学习的分类算法中,支持向量机(Support Vector Machine, SVM)是极具代表性的 "优雅派"------ 它通过寻找 "最优超平面" 实现分类,兼具理论深度与实战价值,至今仍是小样本、高维数据(如图像、文本)分类的优选方案。
一、SVM 的核心目标:找到 "最稳健" 的划分超平面
1. 什么是超平面?
超平面是 SVM 的 "分类工具",本质是n 维空间中分隔不同类别的 n-1 维子空间:
- 2 维空间(平面):超平面是 1 维直线(如
Ax+By+C=0); - 3 维空间:超平面是 2 维平面(如
Ax+By+Cz+D=0); - n 维空间:超平面用通用方程表示为
wᵀx + b = 0(w是超平面的法向量,决定超平面方向;b是偏移量,决定超平面位置)。
2. 为什么需要 "最优" 超平面?
面对两类样本,能分隔它们的超平面有无数个,但 SVM 要找的是对样本扰动 "容忍性最强" 的超平面 ------ 即 "离超平面最近的样本点,距离尽可能远"。这些 "最近的样本点" 就是支持向量(Support Vectors),它们决定了超平面的位置,也是 SVM 名称的由来。
二、SVM 的数学推导:从 "最大化间隔" 到 "求解约束优化"
SVM 的核心是 "最大化支持向量到超平面的距离",这一目标需要通过数学转化为可求解的优化问题。
1. 第一步:定义 "间隔"(Margin)
-
点到超平面的距离 :对于 n 维空间中的样本点
x,到超平面wᵀx + b = 0的距离公式为:d=∥w∥∣w⊤x+b∣
(
\|w\|是法向量w的 L2 范数,即√(w₁²+w₂²+...+wₙ²))。 -
间隔的定义 :间隔是 "两类支持向量到超平面距离之和",即
Margin = 2d(d是单侧支持向量到超平面的距离)。SVM 的目标是最大化间隔 ,本质等价于 "最大化
d"。
2. 第二步:转化为约束优化问题
为了最大化d,需要添加约束条件:所有样本都要在超平面的 "正确一侧",且支持向量到超平面的距离至少为d 。
结合样本标签(y=+1表示正例,y=-1表示负例),约束条件可写为:
yi(w⊤xi+b)≥1(i=1,2,...,n)
(这里做了 "放缩变换":通过调整w和b的尺度,让支持向量满足y_i(w^\top x_i + b) = 1,其他样本满足 "≥1",简化计算)。
此时,"最大化d" 的目标可转化为:
(因)
而 "最大化1/‖w‖" 等价于 "最小化(1/2)‖w‖²"(平方项便于求导,系数1/2不影响最优解)。最终,SVM 的优化问题变为:
minw,b21∥w∥2 s.t. yi(w⊤xi+b)≥1(i=1,2,...,n)
3. 第三步:用拉格朗日乘子法求解
上述是 "带约束的凸优化问题",需用拉格朗日乘子法 将其转化为无约束问题。
构造拉格朗日函数:
L(w,b,α)=21∥w∥2−∑i=1nαi[yi(w⊤xi+b)−1]
其中α_i ≥ 0是拉格朗日乘子,对应每个样本的约束条件。
通过对w和b求偏导并令其为 0,可得到两个关键条件:
w = ∑_{i=1}^n α_i y_i x_i(超平面的法向量w由支持向量的线性组合构成,非支持向量的α_i=0,不影响结果);∑_{i=1}^n α_i y_i = 0(偏移量b的求解条件)。
将w代入拉格朗日函数,最终转化为 "对偶问题":
maxα∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxi⊤xj
s.t. ∑i=1nαiyi=0,αi≥0(i=1,2,...,n)
求解这个对偶问题后,即可得到α,进而通过w和b确定最优超平面。

三、SVM 的关键拓展:解决 "线性不可分" 问题
现实中,很多数据无法用线性超平面分隔(如 "异或问题"),此时需要 SVM 的两个核心技巧:软间隔 和核函数。
1. 软间隔:容忍少量 "噪声样本"
当数据中存在噪声(如异常点)时,"严格线性可分" 的要求过于苛刻,SVM 引入松弛因子ξ_i ≥ 0 ,允许少量样本不满足 "y_i(w^\top x_i + b) ≥ 1",约束条件变为:
yi(w⊤xi+b)≥1−ξi
目标函数也相应调整,增加 "惩罚项" 控制噪声容忍度:
minw,b,ξ21∥w∥2+C∑i=1nξi
其中C是 "惩罚系数":
C越大:对噪声的惩罚越重,要求分类尽可能准确,可能导致过拟合;C越小:对噪声的容忍度越高,可能导致欠拟合。
2. 核函数:将低维数据映射到高维
当数据在低维空间线性不可分时,可通过核函数将其映射到高维空间,使其线性可分。
(1)核函数的核心思想
举个简单例子:2 维空间中 "异或数据"((0,0)、(1,1) 为负例,(0,1)、(1,0) 为正例)无法用直线分隔,但映射到 3 维空间(如φ(x₁,x₂)=(x₁², x₂², √2x₁x₂))后,就能用平面分隔。
但直接映射到高维会面临 "维度灾难"(如 3 维映射到 9 维,100 维映射到 10⁴维,计算量暴增)。核函数的巧妙之处在于:无需显式计算高维映射,直接在低维空间计算高维空间的内积。
即对于样本x和z,核函数K(x,z) = φ(x)^\top φ(z),只需计算K(x,z),就能替代高维内积,大幅降低计算成本。
(2)常用核函数
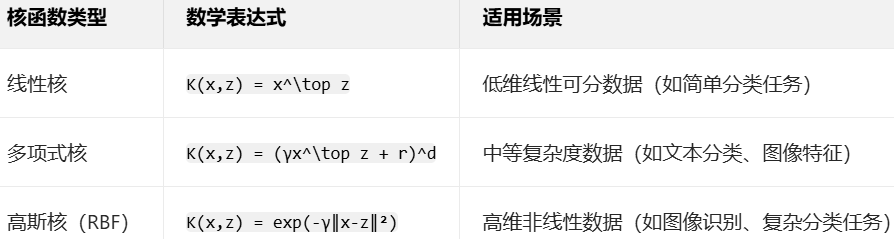
四、SVM 的优缺点与适用场景
优点
- 泛化能力强:基于 "最大化间隔",对噪声不敏感,不易过拟合(尤其小样本数据);
- 适合高维数据:无需降维,能处理特征数远大于样本数的场景(如图像的像素特征);
- 鲁棒性好:仅依赖支持向量,非支持向量的变化不影响超平面;
- 可处理非线性数据:通过核函数轻松应对非线性分类任务。
缺点
- 计算复杂度高:对偶问题的求解时间随样本数增加而增长,不适合超大数据集(如百万级样本);
- 参数调优复杂 :需调整
C(软间隔惩罚系数)和核函数参数,对新手不友好; - 多分类支持弱:原生 SVM 仅支持二分类,多分类需通过 "一对多""一对一" 等策略间接实现。
适用场景
- 小样本、高维数据分类(如图像识别、手写数字识别);
- 非线性分类任务(如复杂模式识别);
- 对泛化能力要求高的场景(如医疗诊断、金融风险预测)。
五、总结
支持向量机是机器学习中 "理论与实践结合" 的典范 ------ 它以 "最大化间隔" 为核心,通过拉格朗日乘子法解决约束优化,用核函数突破线性不可分限制,最终实现高效分类。尽管在超大数据集上的表现不如深度学习,但在小样本、高维数据场景中,SVM 仍有不可替代的优势。