理想汽车智驾方案介绍 3｜MoE+Sparse Attention 高效结构解析

一、前言

在上述两篇系列帖子中，笔者已对理想汽车 VLM 和 VLA 方案的框架进行了全面介绍，但对于其中的前沿技术仅做了初步探讨，未进行更深入的剖析。因此，笔者计划继续以系列文章的形式，介绍其中涉及的相关前沿技术。

首先，将介绍 MindVLA 中采用的"MoE + Sparse Attention"高效结构。

二、MoE + Sparse Attention 高效结构

稀疏注意力（Sparse Attention）与混合专家架构（MoE）是提升大模型效率与性能的核心技术。MindGPT 针对大语言模型（LLM）进行了重新设计与预训练，使其具备了 3D 空间理解和 3D 推理能力，不过这在一定程度上增加了大语言模型（LLM）的参数量。即便采用英伟达（NV）大力宣传的 Thor - U 智驾芯片，在端侧部署时仍有可能会出现推理效率低下的问题。所以模型采用了 MOE 架构+SparseAttention，实现模型容量扩容的同时不会大幅度增加推理负担。

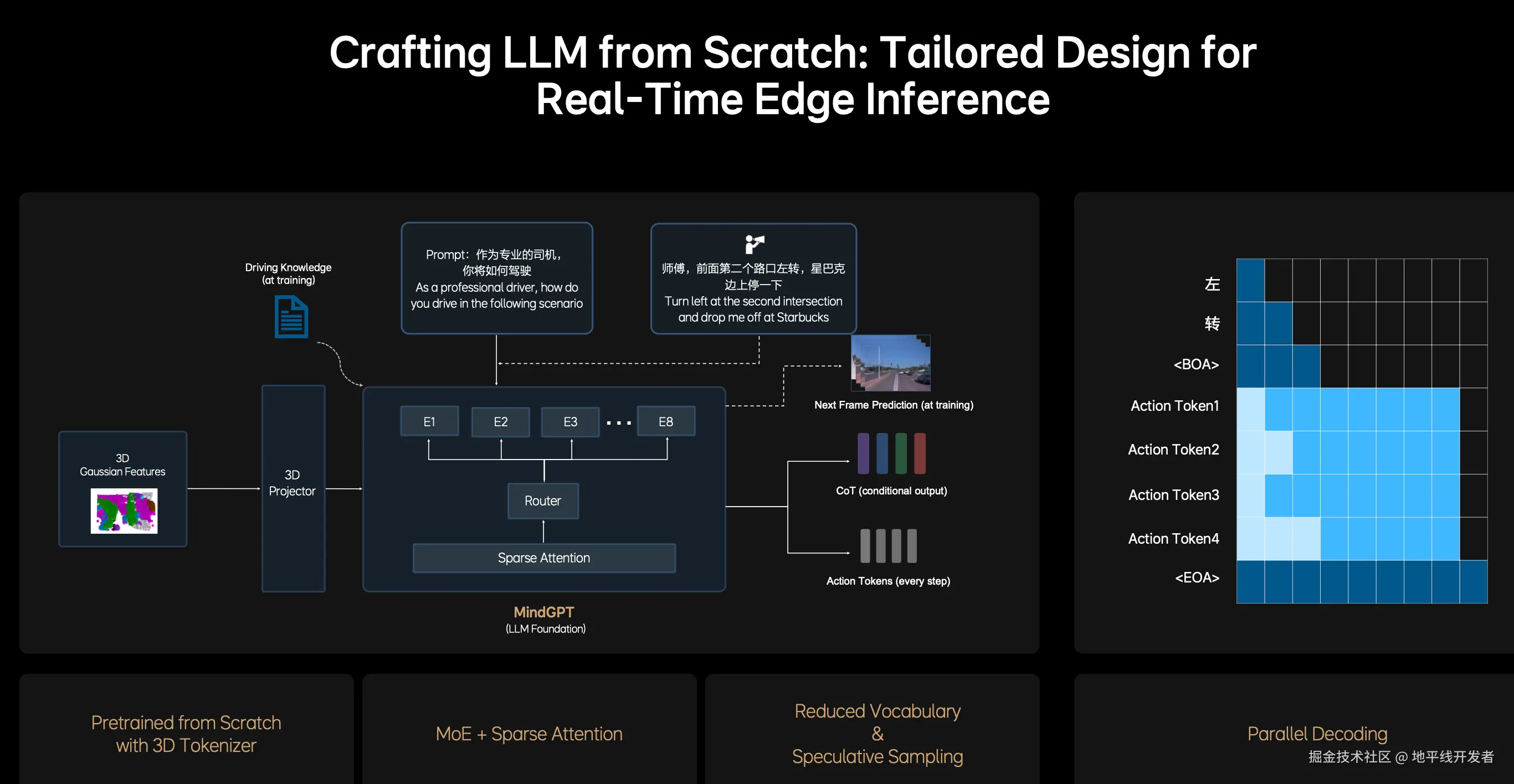
由上图可以看到，MindGPT 使用混合专家（MoE）架构（有 E1-E8 个专家），由 Router 动态选择激活部分专家（而非全部），只在需要时调用相关子模型。稀疏注意力（Sparse Attention）则限制注意力机制的复杂度，只关注关键输入部分（如相关物体或动作），而不是全局计算。在这张图中，它的实现过程是：

每一层的 token 并不全互相注意，而是：

利用 Router 分配 token 给不同的 expert
每个 expert 内部只在局部或关键 token 上建立注意力连接

这种结构既节省计算，又保持了输入的局部结构性，尤其适合 3D 场景中的空间约束。

2.1 Sparse Attention

参考论文Generating Long Sequences with Sparse Transformers

传统 transformer 的全连接注意力复杂度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2)，对于高维空间场景（例如 3D Token 很多）会显著拖慢速度、增加计算。

稀疏注意力的核心目标是：

减少 token-to-token 的注意力连接（只对一部分 token 建立 attention）
降低计算复杂度，同时保持关键 token 的交互质量

那么它是如何实现目标的呢？下面将结合Sparse Transformer代码进行介绍。

Sparse Transformer 是由OpenAI提出的稀疏注意力的最早实现之一，其核心思想是用 规则稀疏模式（Regular Sparse Patterns） 替代标准全连接注意力（full self-attention）。在保持表示能力的同时，将注意力复杂度从

<math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2)降低为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O （ n n ） O（n\sqrt n） </math>O（nn ）.

2.1.1 Sparse Attention 图结构解析

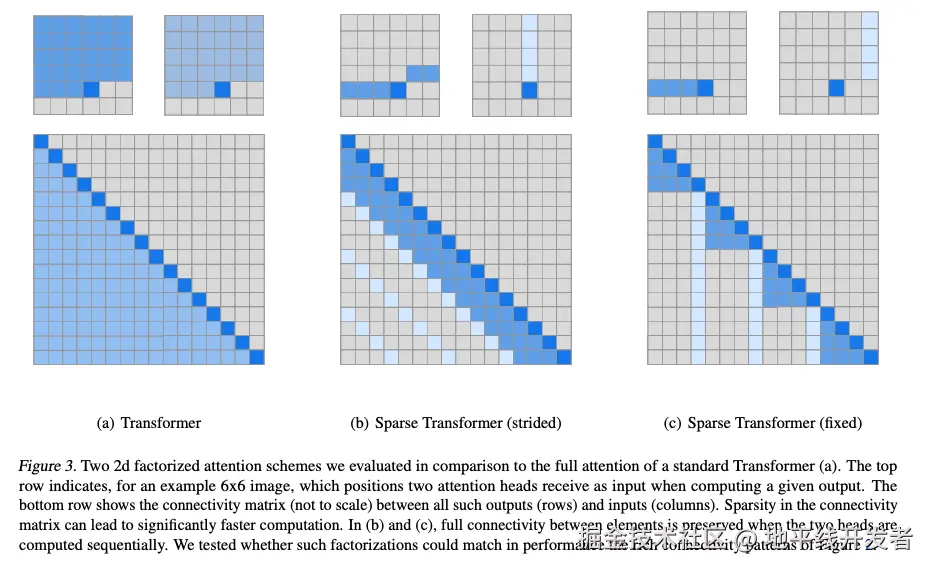
Strided attention（跳跃连接）

每个 token 关注步长为 s 的若干 token，例如：

Plain 复制代码

位置:      0   1   2   3   4   5   6   7   8
strided:   ↑       ↑       ↑       ↑

token 8 会关注 0， 2， 4， 6 这些步长为 2 的 token。

Local attention（局部窗口）

每个 token 也关注自己附近的窗口内 token，比如前后 2 个：

Plain 复制代码

位置:       5
局部窗口:   3   4   5   6   7

组合结构

将两者合并后，注意力图是 局部窗口 + 跳跃连接，形成稀疏但有覆盖力的结构：

Plain 复制代码

Token 位置:         8
局部连接:         6 7 8
跳跃连接:     0 2 4

这种结构可以保证每个 token 都能快速传播到远端（通过跳跃），并同时保留局部建模能力。

2.1.2 代码实现解析

由于 OpenAI Sparse Transformer 没开源，这里参考了其思想的一个流行实现：[OpenNMT-py 或 custom PyTorch 实现]，也可参考 Reformer 等模型实现方式。

稀疏注意力 mask 构造（关键）

Plain 复制代码

def build_sparse_attention_mask(seq_len, block_size=64, num_local_blocks=1, stride=2):
    """
    构造稀疏注意力 mask：局部 + 跳跃
    """
    mask = torch.zeros(seq_len, seq_len, dtype=torch.bool)

    for i in range(seq_len):
        # 添加局部窗口（例如前后1个block）
        for j in range(-num_local_blocks, num_local_blocks + 1):
            idx = i + j * block_size
            if 0 <= idx < seq_len:
                mask[i, idx] = True

        # 添加跳跃连接（stride）
        for j in range(0, seq_len, stride):
            mask[i, j] = True

    return mask

这个 mask 会用于注意力权重：

Plain 复制代码

attn_scores = torch.matmul(query, key.transpose(-2, -1))  # [B, H, N, N]
attn_scores[~mask] = -inf  # 掩蔽非连接位置
attn_probs = softmax(attn_scores)

应用在 Attention 模块

核心 attention 模块不变，只是加了 mask：

Plain 复制代码

def sparse_attention(query, key, value, mask):
    attn_scores = torch.matmul(query, key.transpose(-2, -1))
    attn_scores = attn_scores.masked_fill(~mask, float('-inf'))
    attn_probs = torch.softmax(attn_scores, dim=-1)
    return torch.matmul(attn_probs, value)

这样就可以在不修改 Transformer 主体结构的前提下使用稀疏连接。

以下是一个 9×9 attention matrix 的稀疏连接可视化（● 表示有连接）：

Plain 复制代码

Token ID →
    0 1 2 3 4 5 6 7 8
  ┌──────────────────
0 │●       ●       ●
1 │  ●     ●     ●
2 │    ●   ●   ●
3 │      ● ● ●
4 │      ● ● ●
5 │      ● ● ●
6 │    ●   ●   ●
7 │  ●     ●     ●
8 │●       ●       ●

中间对角线为 **局部 attention，**分布的条纹为 跳跃 attention。

2.1.3 复杂度分析

标准全连接 Self-Attention 的公式是：

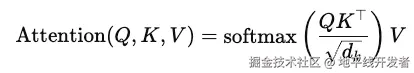
<math xmlns="http://www.w3.org/1998/Math/MathML"> Q K T QK^T </math>QKT：产生 n×n 的权重矩阵 → 计算复杂度是： <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 d ) O(n^2 d) </math>O(n2d);

Softmax ()V : <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 d ) O(n^2 d) </math>O(n2d);

整体复杂度为： <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 d ) O(n^2 d) </math>O(n2d)，这意味着当序列变长时（如 n=8192），计算量和内存都会剧增。

Sparse Transformer 通过限制每个 token 只关注 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ) O(\sqrt{n}) </math>O(n )个位置，从而稀疏 attention 矩阵。

每个 token 的 attention 链接数为 <math xmlns="http://www.w3.org/1998/Math/MathML"> k = O ( n ) k=O(\sqrt{n}) </math>k=O(n )**，**所有 token 的总链接数就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> n ⋅ k = n ⋅ n n⋅k=n⋅\sqrt{n} </math>n⋅k=n⋅n 。

由于只需要对是 <math xmlns="http://www.w3.org/1998/Math/MathML"> n ⋅ n n⋅\sqrt{n} </math>n⋅n 个位置计算 QKᵀ dot product，而不是 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 n^2 </math>n2 ，每个位置依然是**O(d)的向量操作 ，**所以 Sparse Transformer 的复杂度是是 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ⋅ n ) O(n⋅\sqrt{n}) </math>O(n⋅n ) 。

2.2 MoE

MoE（专家混合体）是神经网络的一种架构模式，该模式将一个层或操作（例如线性层、多层感知机或注意力投影）的计算拆分为多个"专家"子网络。这些子网络各自独立地进行计算，其计算结果会被整合，以生成 MoE 层的最终输出。MoE 架构可分为密集型和稀疏型，前者意味着在处理每个输入时都会启用所有专家，后者则表示每个输入仅使用部分专家。因此，MoE 架构具备以下优势：

提升计算效率
在不显著增加推理成本的前提下，扩大模型容量（参数量）

这些优势与大模型的应用难题完美匹配，故而在该领域得到了较为广泛的应用。

2.2.1 MoE 结构解析

本节首先描述 MoE 的核心组件，然后以DeepSpeed-MoE 源代码为例进行详细解析。

以 PyTorch 为例，MoE 的核心组成部分通常包括以下几个模块：

1.`Gate` 模块（路由器）

负责为每个输入样本选择合适的专家（通常是 top-k 策略）：

Plain 复制代码

# 伪代码
scores = gate(x)  # (batch_size, num_experts)
top_k_scores, top_k_indices = torch.topk(scores, k=2)

scores 通常是通过一个线性层获得，表示输入样本对各个专家的偏好程度。
路由器可能带有噪声或正则（如 Switch Transformer 中的 noisy gating）。

2.`Experts` 模块（多个子网络）

每个专家是一个独立的神经网络（比如一个 MLP）：

Plain 复制代码

class Expert(nn.Module):
    def __init__(self, hidden_dim):
        self.ff = nn.Sequential(
            nn.Linear(hidden_dim, 4*hidden_dim),
            nn.ReLU(),
            nn.Linear(4*hidden_dim, hidden_dim)
        )

通常通过参数共享或并行执行多个专家。

3.`Dispatcher`（稀疏调度器）

根据 Gate 的输出，将输入路由给选中的专家，并收集输出：

Plain 复制代码

 for i in range(num_experts):
    expert_input = input[mask[:, i]]
    expert_output = experts[i](expert_input)
    output[mask[:, i]] = expert_output * gate_scores[:, i]

这一步骤通常要做优化，否则容易成为性能瓶颈。

2.2.2 DeepSpeed-MoE 示例代码

源码地址：github.com/microsoft/D...

其核心组件为deepspeed.moe.layer.MoE和deepspeed.moe.layers.gates 类。

1.`MoE` 类（ `deepspeed.moe.layer.MoE`）

作为入口类，集成了路由器、专家、通信逻辑：

Plain 复制代码

class MoE(nn.Module):
    def __init__(self, hidden_size, experts=..., ep_size=..., k=1):
        self.experts = Experts()
        self.gate = TopKGate()
        ...

ep_size：每个专家组的并行数（Expert Parallelism）。
k: top-k gating.
使用了通信优化如 All-to-All 分发样本。

2.构造函数 `init`

根据官方文档，MoE 的初始化签名如下，参数丰富且功能强大：

Plain 复制代码

class MoE(nn.Module):
    def __init__(self,
                 hidden_size: int,
                 expert: nn.Module,
                 num_experts: int = 1,
                 ep_size: int = 1,
                 k: int = 1,
                 capacity_factor: float = 1.0,
                 eval_capacity_factor: float = 1.0,
                 min_capacity: int = 4,
                 use_residual: bool = False,
                 noisy_gate_policy: Optional[str] = None,
                 drop_tokens: bool = True,
                 use_rts: bool = True,
                 use_tutel: bool = False,
                 enable_expert_tensor_parallelism: bool = False,
                 top2_2nd_expert_sampling: bool = True)

hidden_size：输入和输出的维度；
expert：作为子模块传入的专家网络（如 MLP）；
num_experts：专家总数；
ep_size：专家并行维度；
k：选用 top‑k 路由；
capacity_factor 和 eval_capacity_factor：训练/评估期间专家最大处理 token 数比例；
min_capacity：每个专家至少能接收的 token 数；
use_residual：是否启用 Residual MoE 结构；
noisy_gate_policy、drop_tokens、use_rts：路由噪声、token 丢弃、随机选择；
enable_expert_tensor_parallelism：专家参数 tensor 切分；
top2_2nd_expert_sampling：top‑2 第二专家采样策略。

这些选项为 MoE 的训练/推理提供了高度灵活性

3.前向函数 forward

forward 函数定义如下：

Plain 复制代码

def forward(self, hidden_states: Tensor, used_token: Optional[Tensor] = None) -> Tuple[Tensor, Tensor, Tensor]:

返回三元组 (output, l_aux, exp_counts)，分别为输出、auxiliary loss、各专家激活次数

forward 函数的核心步骤可以总结为以下 5 部分：

Plain 复制代码

def forward(self, hidden_states, used_token=None):
    # 1️⃣ Gating 阶段：计算每个 token 的专家 logits，并选出 top‑k 专家
    gates, load, indices, expert_capacity = self.gate(
        hidden_states, self.training)
    # gates: (B, k) 专家权重，load: auxiliary balance loss，indices: 专家索引

    # 2️⃣ Capacity 控制：根据 capacity_factor 限制每个专家最多处理的 token 数
    # 用 expert_capacity 来计算实际可接收的 token 数

    # 3️⃣ Dispatch 阶段：将 token 分发给对应专家
    dispatch_mask, combine_mask = create_masks(indices, expert_capacity)
    # dispatch_mask: 用于提取每个专家的 token

    # 重塑 hidden_states 方便通信：
    expert_inputs = torch.einsum("b h, b e -> e b h", hidden_states, dispatch_mask)

    # 4️⃣ all_to_all 分发 token：跨 GPU 路由 token 到对应专家所在 GPU
    expert_inputs = all_to_all(expert_inputs, self.expert_parallel_group)

    # 5️⃣ 专家计算阶段：每个专家在本地 receive 的 token 上执行 forward
    expert_outputs = self.experts(expert_inputs)

    # 6️⃣ all_to_all 收集结果：各专家输出回传给原始 GPU
    expert_outputs = all_to_all(expert_outputs, self.expert_parallel_group)

    # 7️⃣ 合并输出：将专家输出按照 token-group 重组回 batch 维度
    output = torch.einsum("e b h, b e -> b h", expert_outputs, combine_mask)

    return output, load, indices.bincount(...)

4.`TopKGate` 类（ `deepspeed.moe.layers.gates`）

实现 top-k 路由，并支持 noisy gate：

Plain 复制代码

class TopKGate(nn.Module):
    def forward(self, input):
        logits = self.w_gating(input)
        topk_vals, topk_indices = torch.topk(logits, k)
        ...

还包括负载均衡 loss。

5.Expert 通信部分

使用 all_to_all 通信分发数据，保证跨 GPU 的负载均衡和数据交换效率。

在多 GPU（分布式）训练中，如果我们有多个专家网络（Experts），这些专家可能是跨 GPU 分布的。举个例子：

有 4 张 GPU，每张 GPU 上部署 2 个专家，共 8 个专家；
假设 batch 里的一部分 token 需要被路由到第 3 个专家（在 GPU 2 上），另一部分需要被送到第 6 个专家（在 GPU 4 上）；
那么就必须跨 GPU 发送这些 token ------ 所以通信效率就非常关键。

这时候就需要 all_to_all 机制来高效完成这个通信过程。

torch.distributed.all_to_all 是一种跨 GPU 的点对点通信机制，作用是每张 GPU 都给其他所有 GPU 发送一块数据，同时从其他 GPU 收到对应的数据块。

具体来说：

每个进程（GPU）上都有自己的输入 token；
每个进程根据路由器（Gate）的输出，将 token 分为 N 份，分别属于 N 个专家（也就是 N 个目标 GPU）；
然后用 all_to_all 一次性把这 N 份数据分发到对应的 GPU 上；
所有专家完成前向计算后，再用 all_to_all 把结果发回。

参考 deepspeed/moe/utils/all_to_all.py：

Plain 复制代码

def all_to_all(input, group):
    # input shape: (num_local_experts, tokens_per_expert, hidden_size)
    output = torch.empty_like(input)
    torch.distributed.all_to_all_single(output, input, group=group)
    return output

通常输入需要 reshape 成：

Plain 复制代码

[local_experts, tokens_per_expert, hidden_dim]

之后经过两次 all_to_all：

tokens 分发阶段：将 token 从本地发送到它所需的专家所在的 GPU；
结果收集阶段：将处理后的输出再收集回原始的 GPU。

参考链接

Applying Mixture of Experts in LLM Architectures

www.cnblogs.com/thesevenths...

zhuanlan.zhihu.com/p/188897585...

理想汽车智驾方案介绍 3｜MoE+Sparse Attention 高效结构解析

一、前言

二、MoE + Sparse Attention 高效结构

2.1 Sparse Attention

2.1.1 Sparse Attention 图结构解析

Strided attention（跳跃连接）

Local attention（局部窗口）

组合结构

2.1.2 代码实现解析

稀疏注意力 mask 构造（关键）

应用在 Attention 模块

2.1.3 复杂度分析

2.2 MoE

2.2.1 MoE 结构解析

1.Gate 模块（路由器）

2.Experts 模块（多个子网络）

3.Dispatcher（稀疏调度器）

2.2.2 DeepSpeed-MoE 示例代码

1.MoE 类（ deepspeed.moe.layer.MoE）

2.构造函数 init

3.前向函数 forward

4.TopKGate 类（ deepspeed.moe.layers.gates）

5.Expert 通信部分

参考链接

1.`Gate` 模块（路由器）

2.`Experts` 模块（多个子网络）

3.`Dispatcher`（稀疏调度器）

1.`MoE` 类（ `deepspeed.moe.layer.MoE`）

2.构造函数 `init`

4.`TopKGate` 类（ `deepspeed.moe.layers.gates`）