线性回归深度解析
第一章 基础理论体系
1.1 本质与定义
-
核心思想:建立自变量(特征)与因变量(目标)的线性映射关系
-
参数意义:
-
wi:特征权重(斜率),反映特征贡献度
-
b:偏置项(截距),修正系统误差
-
-
统计学视角:最小化残差平方和的参数估计方法
1.2 分类与结构
| 类型 | 数学模型 | 适用场景 | 几何意义 |
|---|---|---|---|
| 一元线性回归 | y=wx+b | 单因素影响分析 | 二维平面拟合直线 |
| 多元线性回归 | y=Xw+b | 多因素联合作用研究 | 高维空间拟合超平面 |
1.3 应用场景深度剖析
-
经济学:GDP与失业率关联分析、消费支出预测
-
生物医学:药物剂量与疗效关系建模、基因表达量分析
-
工业控制:设备参数与良品率相关性研究
-
气候科学:CO₂浓度与气温变化趋势预测
第二章 数学原理与优化
2.1 损失函数数学本质
-
目标函数:残差平方和最小化
-
概率解释:极大似然估计视角下,假设误差服从高斯分布
2.2 优化算法数学推导
2.2.1 正规方程法
-
矩阵解 :
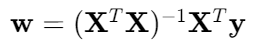
-
存在性条件 :
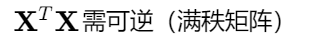
-
复杂度分析 :

2.2.2 梯度下降法
-
参数更新公式:
-
学习率α的选取:
-
过大:震荡发散(α>0.01风险)
-
过小:收敛缓慢(α<10−5低效)
-
2.2.3 算法变种对比
| 算法 | 更新规则 | 收敛性 | 适用场景 |
|---|---|---|---|
| 批量梯度下降 | 全样本计算梯度 | 稳定但缓慢 | 小型数据集(<10⁴) |
| 随机梯度下降 | 单样本更新梯度 | 快但波动大 | 在线学习场景 |
| 小批量梯度下降 | 每轮取k个样本(16≤k≤512) | 速度与稳定平衡 | 工业级大规模数据 |
第三章 模型评估科学体系
3.1 误差指标全解
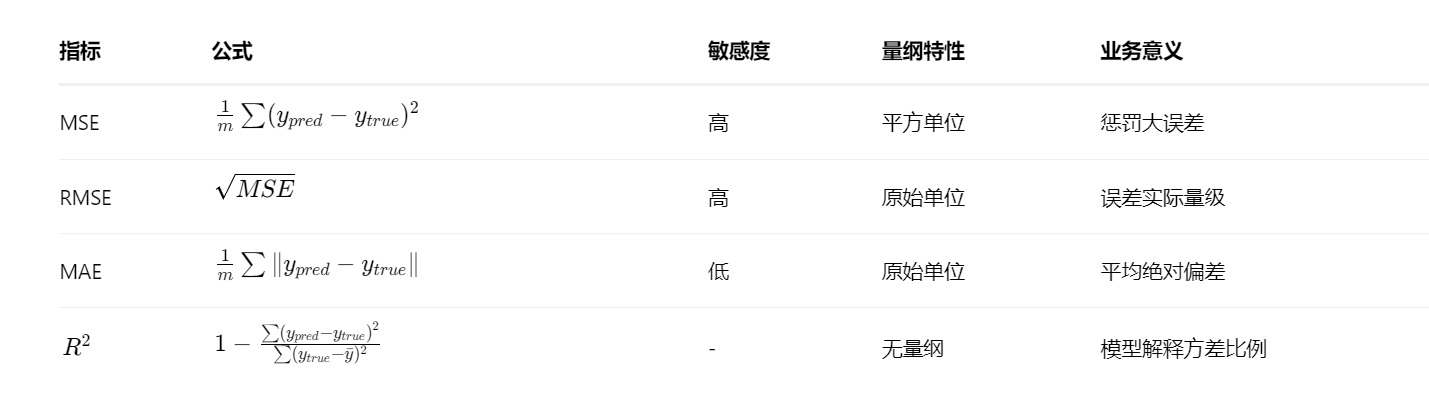
3.2 评估误区警示
-
陷阱1:仅关注训练集R2>0.9可能暗示过拟合
-
陷阱2:MSE与量纲相关,跨数据集比较需标准化
-
黄金准则:测试集性能>训练集性能
第四章 泛化能力提升策略
4.1 欠拟合解决路径
-
特征工程:
-
特征交叉:x3=x1×x2
-
多项式扩展:x2,x3,x
-
分箱处理:连续变量离散化
-
-
模型升级:
-
引入非线性基函数
-
切换为决策树等复杂模型
-
4.2 过拟合控制体系
4.2.1 正则化数学原理
-
L1正则(Lasso):
-
几何解释:菱形约束域,顶点导致稀疏解
-
特征选择:自动筛选关键特征
-
-
L2正则(Ridge):
-
几何解释:圆形约束域,平滑权重分布
-
优势:严格凸函数,解唯一稳定
-
4.2.2 正则化参数λ选择
-
λ↑:模型复杂度↓,可能欠拟合
-
λ↓:模型复杂度↑,过拟合风险
-
交叉验证法:网格搜索确定最优λ
4.2.3 其他过拟合抑制技术
-
早停法(Early Stopping):验证集误差上升时终止训练
-
Dropout:训练中随机丢弃神经元(神经网络)
-
数据增强:生成合成样本扩大数据集
第五章 工业实践方法论
5.1 特征工程最佳实践
-
预处理流程:
-
缺失值处理:中位数填充/预测填充
-
异常值处理:3σ原则/四分位距法
-
标准化:
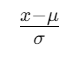 (高斯分布)
(高斯分布) -
归一化:
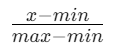 (均匀分布)
(均匀分布)
-
5.2 模型部署陷阱规避
-
特征偏移:线上数据分布变化导致性能衰减
- 解决方案:定期模型重训练
-
解释性需求:
-
权重分析:wi符号与大小业务解释
-
SHAP值:量化特征贡献度
-
5.3 创新应用前沿
-
联邦学习:跨机构联合建模保护数据隐私
-
贝叶斯线性回归:引入先验分布量化不确定性
-
鲁棒回归:Huber损失函数抵抗异常值