目录
[1 U-Net 论文解读](#1 U-Net 论文解读)
[1.1 研究背景](#1.1 研究背景)
[1.2 方法论](#1.2 方法论)
[1.3 创新点](#1.3 创新点)
[1.4 实验结果分析](#1.4 实验结果分析)
[1.5 总结及局限分析](#1.5 总结及局限分析)
[2 Sinkhorn 算法](#2 Sinkhorn 算法)
[2.1 最优传输问题的新形式](#2.1 最优传输问题的新形式)
[2.2 Sinkhorn 算法的目标及迭代](#2.2 Sinkhorn 算法的目标及迭代)
[2.3 Sinkhorn 算法的优缺及应用](#2.3 Sinkhorn 算法的优缺及应用)
[3 总结](#3 总结)
摘要
本周首先阅读了 U-Net 的论文,了解了 U-Net 的背景、架构、创新点与优势,同时分析了它的局限性;其次学习了Sinkhorn 算法,拓展了最优传输问题的表示形式,了解了算法的目标、步骤、优缺点以及应用场景。
Abstarct
This week, I first read the U-Net paper, gaining an understanding of its background, architecture, innovations, and advantages, while also analyzing its limitations. Next, I studied the Sinkhorn algorithm, expanding my knowledge of the representation forms of optimal transport problems, and learned about its objectives, procedures, strengths and weaknesses, as well as application scenarios.
1 U-Net 论文解读
U-Net 是由 Olaf Ronneberger 等人在2015年提出的一种全卷积网络架构,最初发表于 MICCAI 会议论文《U-Net: Convolutional Networks for Biomedical Image Segmentation》(链接:U-Net: Convolutional Networks for Biomedical Image Segmentation - 百度学术)。该架构因其卓越的边界保持能力和小样本学习效率,迅速成为生物医学图像分割领域的基准模型。
1.1 研究背景
在2013~2015年,深度卷积网络在许多视觉识别任务中都表现优异,但容易受到可用训练集以及网络大小的限制。在生物医学图像处理中,这一缺陷尤为明显,因为在该领域任务中通常很难获取大量的训练图像,图像中的目标结构经常呈现出不规则的形态和复杂的纹理变化,相邻组织之间的边界也模糊不清。
为了解决这个问题,当时的主流方法是 Ciresan 等人提出的滑动窗口卷积网络(链接:Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images - 百度学术),通过为每个像素提取局部区域进行分类。这种方法能够提升定位能力,但必须为每个重叠的补丁单独运行网络,计算冗余极大;同时,感受野大小与定位精度之间需要进行权衡,大感受野需要更多池化层,会导致空间信息损失,而小感受野则无法捕获足够的上下文信息。
1.2 方法论
U-Net 的核心思想是通过对称的编码器-解码器架构结合跳跃连接,实现多尺度特征的提取与融合。整个网络结构呈现完美的U形对称,左侧是编码路径,右侧是解码路径。其结构如下图:
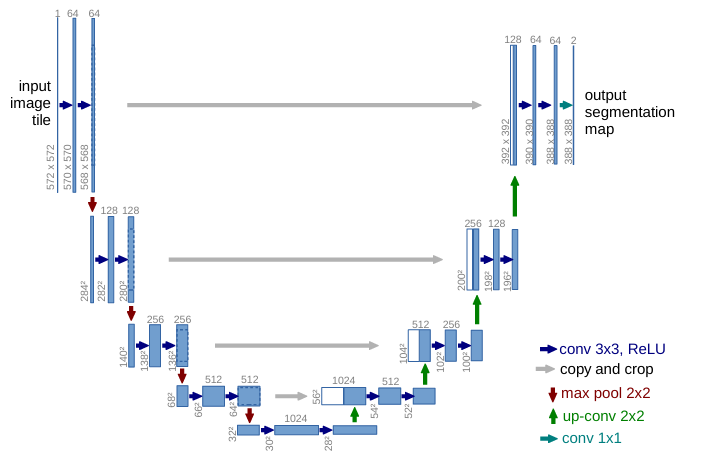
编码器路径通过连续的卷积和池化操作,逐步扩大感受野并提取多层次特征,这一过程类似于人类视觉系统的抽象化处理,即从局部边缘、纹理等低层特征逐渐整合为高层语义信息;解码器路径则执行相反的过程,通过上采样操作逐步恢复空间维度,将高层语义信息与空间细节重新融合;二者再通过有别于传统编码器-解码器设计的跳跃连接进行特征图拼接,即将编码器每一层输出的特征图直接传递到解码器的对应层,使解码器在重建特征时能够同时访问高层语义特征和低层细节特征。
同时,面对医学可训练图像稀缺的挑战,论文提出了一套完整而巧妙的训练策略。数据增强方面,作者没有局限于传统的旋转、缩放等简单变换,而是引入了弹性形变这一专门针对生物组织特性的增强方法;在损失函数设计上,作者采用了加权交叉熵损失,为每个像素分配不同的权重,使得网络更加关注两类像素之间的边界区域,这恰好是医学图像分割中最具挑战性的部分。
1.3 创新点
也因此,U-Net 的设计主要有如下几个创新点。
首先,它提出了一个新的网络结构,即独特的U形对称架构与跳跃连接的有机结合。一方面,不同于当时常见的简单上采样网络,U-Net 的解码路径拥有与编码路径对称的特征通道数,这使得上下文信息能够有效地传播到高分辨率层。另一方面,跳跃连接不是简单的残差相加,而是通道拼接,能够完整保留编码器的多尺度特征信息。这种设计思想的影响远远超出了医学图像领域,成为后来众多分割网络的基础架构。即使是在 Transformer 架构兴起的今天,许多最先进的分割模型仍然保留了U形结构和跳跃连接的基本思想,只是将卷积模块替换为自注意力模块。
其次,它采用了针对小样本以及领域特性的的弹性形变数据增强策略。在医学图像领域,标注数据极少是普遍问题,传统的数据增强方法如旋转、缩放也不足以模拟生物组织的复杂形变。故论文提出的基于位移场的弹性形变,使之能够生成逼真的新样本,极大地提高了数据的利用效率,使网络学会对形变的不变性。这一方法在后来成为了医学图像增强的标准技术之一。
接着,它优化了加权损失函数的设计,主要是对细胞边界区域的权重进行强化。通过形态学操作计算细胞边界,并为这些狭窄区域分配高权重,网络被强制学习区分接触的细胞实例,解决了医学图像分割中常见的粘连物体分割难题。
最后,它进行了完整的全卷积设计,并采用了重叠切片策略。一方面,网络不含全连接层,可以处理任意尺寸的输入;另一方面,通过重叠切片策略(输入图像扩展、镜像填充缺失区域等),实现了对大图像的无缝分割,克服了GPU内存限制。
1.4 实验结果分析
论文主要在三个具有挑战性的生物医学分割任务上验证了U-Net的有效性。
在 ISBI 2012 电子显微镜神经元结构分割挑战中,U-Net 仅使用30张训练图像,在没有复杂后处理的情况下,其包裹误差为 0.0003529 ,兰德误差为 0.0382 ,显著超越了 Ciresan 等人的滑动窗口方法(误差分别为0.000420 和 0.0504)。当时排名中只有使用了大量数据集特定后处理的方法在兰德误差上略优于 U-Net,但它们的包裹误差更高,且需要提交 78 个不同解决方案才能达到这一结果。这一结果证明了 U-Net 在小样本学习上的强大能力。
p.s. 包裹误差,Warping Error,主要衡量分割边界的准确性;兰德误差,Rand Error,主要衡量的是像素级的分割一致性,评估的是哪些像素应该被分在同一个区域。这两者是图像分割算法的重要评估指标。
在 ISBI 2015 细胞追踪挑战的两个数据集上,U-Net 的优势就更加明显。在 PhC-U373 数据集(35张训练图像)上获得了 92.03% 的平均 IoU,远超第二名的83%;在更具挑战性的 DIC-HeLa数据集(20张训练图像)上获得了 77.56% 的 IoU,而第二名仅为46%。这种性能差距表明U-Net特别擅长处理对比度低、边界模糊的微分干涉相差显微镜图像。
p.s. IoU(交并比,Intersection over Union),也称为 Jaccard Index(杰卡德系数),是计算机视觉和图像分割领域最核心、最直观的评价指标之一。
实验还揭示了几个关键发现。第一,弹性形变增强对性能提升至关重要,特别是在训练数据极少的情况下;第二,加权损失函数显著改善了细胞边界的分割质量,减少了粘连错误;第三,重叠切片策略使得网络能够处理任意尺寸的图像,而无需调整网络结构或牺牲分辨率。在训练效率上,在NVIDIA Titan GPU 上仅需10小时即可完成训练,分割一张 512x512 图像不到1秒,满足了实际应用的实时性要求。此外,误差分析显示,U-Net 主要的失败案例发生在细胞边界极度模糊或多个细胞严重重叠的区域,但这些情况即使是人工标注也存在困难。
1.5 总结及局限分析
总的来说,实验结果不仅定量证明了U-Net的卓越性能,还定性展示了其在保留细节和正确处理复杂拓扑结构方面的能力,为后续的医学图像分割研究设立了新的基准。
但尽管 U-Net 取得了巨大成功,但冷静分析其局限性有助于我们理解后续研究的发展方向。
U-Net 的一个明显局限是对计算资源的需求。随着网络深度的增加和输入图像尺寸的增大,内存消耗会呈指数级增长。而且,U-Net 的跳跃连接虽然有利于信息流动,但也可能导致特征图的通道数急剧增加,特别是在解码器的深层,这会进一步加剧计算负担。另外,U-Net 的设计初衷是针对二维图像分割,对于三维医学图像数据(如CT、MRI),直接扩展为3D UNet虽然可行,但计算成本会更加高昂。
另一个局限性就是 U-Net 对多尺度信息的处理方式相对简单,虽然不同层次的特征图通过跳跃连接进行了融合,但这种融合是线性的拼接操作,网络需要学习如何有效利用这些多尺度信息,这一过程并不总是高效。
2 Sinkhorn 算法
Sinkhorn 算法是一种用于计算两个概率分布之间的最优传输距离的迭代算法,它通过引入熵正则化将原本的最优传输问题转化为一个可以通过迭代矩阵缩放来求解的问题,本质上也是求解一个带有熵正则化的最优传输问题的对偶形式。
2.1 最优传输问题的新形式
除了前面学习的表达形式,即:
在实际应用中,最优传输问题还可表示为,给定一个m维的概率向量 a(对应 m 个目标分布),一个 n 维概率向量 b(对应 n 个初始分布),一个 m x n 的成本矩阵 C(其中每个元素 对应从初始分布 j 到目标分布 i 的单位成本),一个非负的传输矩阵 P(其中每个元素
对应从初始分布 j 到目标分布 i 的运输量),其行和等于 a,列和等于 b,因为其第 i 行对应第 i 个目标分布(列同理),即:
这样才能使所有初始分布正好映射到所有目标分布。
然后,基于上述条件,需要寻找到能使 P、C 内积最小( )的 P。因为两个矩阵做内积运算,对于单个元素 ,
代表从初始分布 j 到目标分布 i 的总成本;对于整体,
意味着所有运输路线成本的总和。只要使其最小,就代表对应的方案花费的成本最低。
2.2 Sinkhorn 算法的目标及迭代
Sinkhorn 算法主要就是在原始最优传输的目标函数中,加上一个熵正则化项,即使其目标函数变为:
其中 是正则化系数,
是矩阵 P 的熵。
这个熵可以使目标函数严格凸,有唯一解,解的结构为 。其中 K 是由成本矩阵 C 决定的(
),成本越低,K 值越大;u ,v 则是行和列的缩放因子,用于满足边际约束进而,原本寻找矩阵 P 的问题就转化为了寻找向量 u 和 v 的问题,而约束条件就变成了:
其中, 表示逐元素乘法;diag(u)与 diag(v)代表行缩放与列缩放矩阵。
对于寻找向量 u 和 v 的问题,Sinkhorn 算法用了一种极其简单优雅的交替归一化(Alternating Normalization)来解决,其步骤如下:
首先,进行初始化,设 为全 1 向量,
;
其次,进行交替迭代,直至 u 和 v 的变化很小,即几乎同时满足行约束与列约束。每次迭代的步骤大致如下:
1.行缩放:更新 u,使得当前矩阵的行和等于 a 以满足行约束;
2.列缩放:但进行行缩放后,矩阵的的列约束会被破坏,所以需要更新 v,使得当前矩阵的列和等于 b。
2.3 Sinkhorn 算法的优缺及应用
Sinkhorn 算法的主要优点在于其每次迭代是矩阵-向量乘法,复杂度 O(mn),且只需很少迭代(通常几十次)就能收敛,比线性规划速度快几个数量级;矩阵运算极易在GPU上并行化,非常适合深度学习。整个迭代过程由可微的基本运算构成,可以轻松嵌入神经网络进行反向传播,这是它相比线性规划在深度学习中的一个重要优势。
除此之外,Sinkhorn 算法是正则化可控的,需要对精度与效率进行权衡。 越大,熵项主导,解更平滑、计算更快,但偏离原始OT问题;
越小,则越接近原始解,但数值稳定性就会变差。这
Sinkhorn 算法直接在指数级上进行计算,十分容易导致数值溢出,所以在实际应用中通常会在对数域操作,即使用 和
进行迭代。
它的主要应用场景之一毫无疑问就是计算分布间距离,作为Wasserstein距离的平滑近似用于比较概率分布。另外还可以应用在词汇、形状、颜色等的匹配,生成模型,以及计算几何与图形学等领域。
3 总结
本周首先阅读了 U-Net 的论文,了解了 U-Net 架构与新的数据增强策略,下周可能尝试用代码进行梳理或者实战;其次对 Sinkhorn 算法进行了大致的学习,了解了它是如何通过引入熵正则化来简化求解最优传输问题的,不过感觉迭代过程有点半懂,下周考虑利用代码或者手动进行梳理。