【算法通关】双指针技巧深度解析:从基础到巅峰(Java 最优解)

我的主页: 寻星探路
个人专栏: 《JAVA(SE)----如此简单!!! 》 《从青铜到王者,就差这讲数据结构!!!》
《数据库那些事!!!》 《JavaEE 初阶启程记:跟我走不踩坑》
《JavaEE 进阶:从架构到落地实战 》 《测试开发漫谈》
《测开视角・力扣算法通关》 《从 0 到 1 刷力扣:算法 + 代码双提升》
《Python 全栈测试开发之路》
没有人天生就会编程,但我生来倔强!!!
寻星探路的个人简介:


在处理数组相关算法时,双指针(Two Pointers) 能够巧妙地利用区间单调性或位置关系,将原本需要 的暴力搜索优化至 。本文精选四道经典题型,附带保姆级代码注释。
一、 移动零 (Move Zeroes) ------ 快慢指针
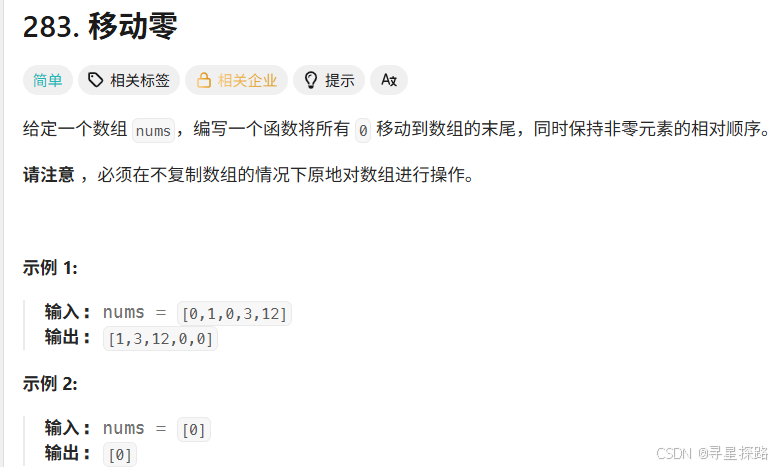
1. 算法思路
- 慢指针 (
slow):指向"下一个非零元素应该存放的位置"。 - 快指针 (
fast):遍历数组,寻找非零元素。 - 通过交换,非零元素被"推"到前面,零自然被"挤"到了后面。
2. Java 代码实现
java
class Solution {
public void moveZeroes(int[] nums) {
// slow 指针之前(不含 slow)全是非零数
int slow = 0;
for (int fast = 0; fast < nums.length; fast++) {
// 当快指针发现非零数时
if (nums[fast] != 0) {
// 如果快慢指针不相等,说明中间有 0,需要交换
if (fast > slow) {
int temp = nums[slow];
nums[slow] = nums[fast];
nums[fast] = temp;
}
// 无论是否交换,slow 都要后移,因为当前 slow 位置已被非零数占据
slow++;
}
}
}
}二、 盛最多水的容器 (Container With Most Water) ------ 左右指针
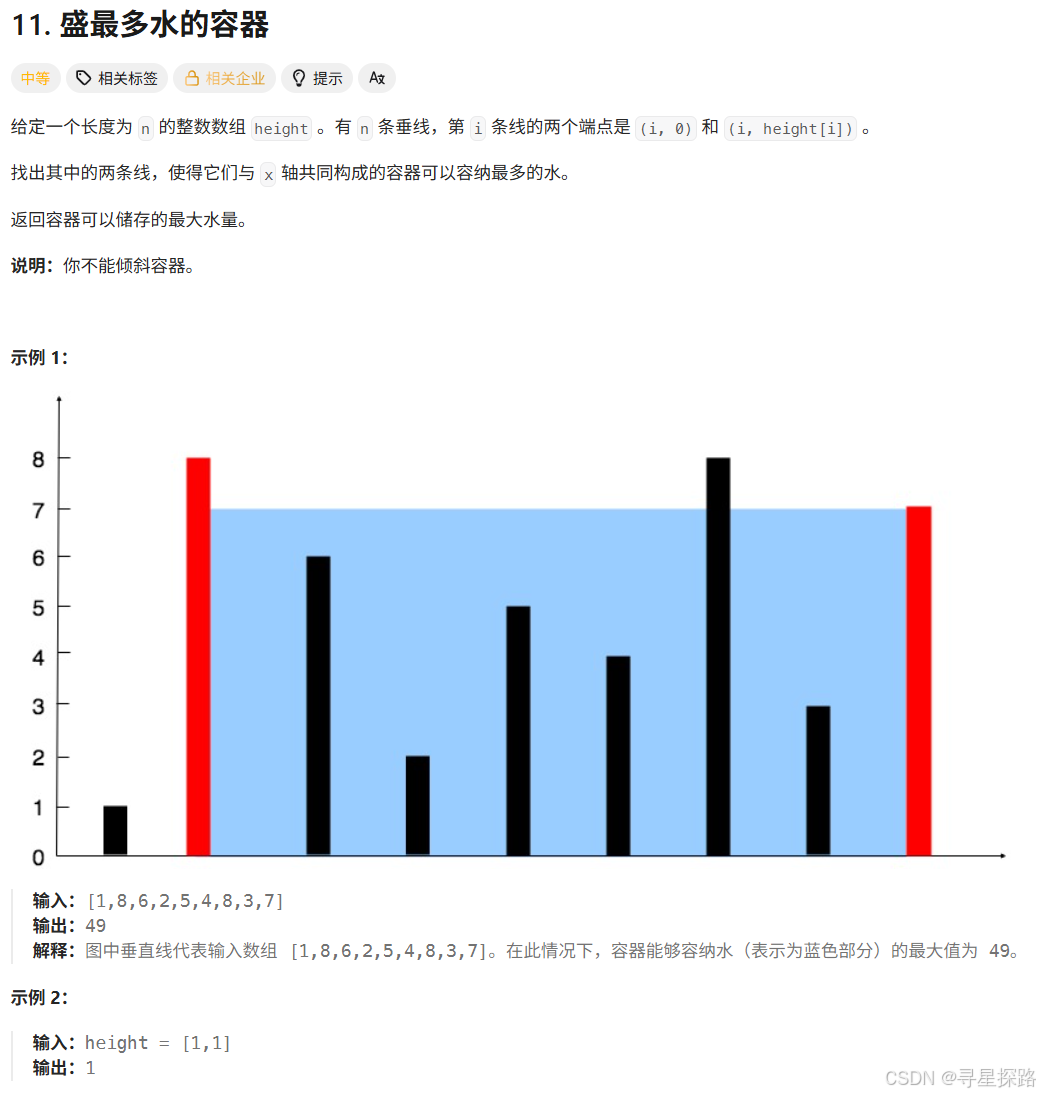
1. 算法思路
- 核心原理:木桶效应。容量由"短板"决定。
- 指针移动逻辑:若移动长板,宽度减小,高度依然受限于短板,容量只会变小;只有移动短板,才可能换来更高的高度。
2. Java 代码实现
java
class Solution {
public int maxArea(int[] height) {
int left = 0, right = height.length - 1; // 定义左右边界
int max = 0; // 存储最大面积
while (left < right) {
// 1. 计算当前面积:宽 (right - left) * 高 (左右两端的最小值)
int currentArea = Math.min(height[left], height[right]) * (right - left);
// 2. 更新全局最大面积
max = Math.max(max, currentArea);
// 3. 贪心策略:哪边矮,就移动哪边的指针
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return max;
}
}三、 三数之和 (3Sum) ------ 排序 + 左右指针

1. 算法思路
- 排序:使数组有序,方便使用双指针并进行去重。
- 枚举 :固定第一个数
a,在剩下的区间里通过双指针寻找b和c,使得a + b + c = 0。
2. Java 代码实现
java
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
Arrays.sort(nums); // 1. 先排序
int n = nums.length;
for (int i = 0; i < n; i++) {
// 如果当前数大于 0,由于数组有序,后续三个数之和一定大于 0
if (nums[i] > 0) break;
// 2. 对第一个数 a 去重:如果当前数和前一个数相同,跳过
if (i > 0 && nums[i] == nums[i - 1]) continue;
int left = i + 1, right = n - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0) {
ans.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 3. 对第二个数 b 去重
while (left < right && nums[left] == nums[left + 1]) left++;
// 4. 对第三个数 c 去重
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
} else if (sum < 0) {
left++; // 和太小,左指针右移增加数值
} else {
right--; // 和太大,右指针左移减小数值
}
}
}
return ans;
}
}四、 接雨水 (Trapping Rain Water) ------ 双指针巅峰

1. 算法思路
- 单点逻辑:位置 能接的水 = 。
- 双指针优化:我们不需要预处理所有高度,只需要用两个指针从两侧向中间靠拢。
2. Java 代码实现
java
class Solution {
public int trap(int[] height) {
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0; // 记录左边和右边遇到的最高高度
int res = 0;
while (left < right) {
// 更新左右两侧目前的最高墙
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
// 如果左边的墙比右边的墙矮
// 意味着:对于 left 这个点,接多少水取决于左侧的 leftMax(因为右侧一定有比它更高的墙)
if (leftMax < rightMax) {
res += (leftMax - height[left]);
left++;
} else {
// 反之,right 这个点接多少水取决于右侧的 rightMax
res += (rightMax - height[right]);
right--;
}
}
return res;
}
}💡 总结:双指针解题的思考模版
- 场景识别:
- 同向指针(快慢指针):常用于处理"原地修改"或"寻找循环/中点"。
- 相向指针(对撞指针):常用于处理"有序数组寻找两数/多数之和"或"区间极值(盛水/接水)"。
- 核心三要素:
- 指针初始化 :是
(0, length-1)还是(0, 0)? - 移动条件:什么情况下左移?什么情况下右移?(通常依据单调性判断)。
- 收缩条件:如何有效跳过重复解(去重)以保证效率?
通过以上四道题的练习,你应该能感受到双指针在降低时间复杂度方面的巨大威力。
感谢你的阅读!如果觉得代码注释对你有帮助,欢迎点赞和收藏!