量子计算：从抽象算法到物理实现的跨学科革命

在计算科学的前沿，一场静默的革命正在低温真空室和理论物理的抽象数学中孕育。这不仅仅是关于更快的处理器，而是关于一种全新的计算范式本身------量子计算。它承诺解决经典计算机无法企及的难题，但其实现之路，是一条融合了数学、计算机科学、材料物理和精密工程的复杂之路。

一、核心原理：超越0与1的世界的

传统计算机基于比特（Bit），非0即1。量子计算机的基石是量子比特（Qubit）。凭借量子力学两大特性，量子比特实现了指数级的信息承载和处理能力：

1. 叠加（Superposition） ：一个量子比特可以同时是0和1，其状态是两者概率幅的叠加。n个量子比特的系统可以同时处于2ⁿ种可能状态的叠加中。这赋予了量子计算机无与伦比的并行性。

2. 纠缠（Entanglement）：无论相距多远，多个量子比特可以形成一种"神秘"的关联，一个比特的状态会瞬间影响另一个。这是实现量子并行计算和纠错的关键。

然而，真正的力量并非来自并行性本身。如果只是同时计算所有答案然后去读取，量子叠加态会坍缩，你只会得到一个随机结果。其精髓在于干涉（Interference）。

二、算法与编程：操纵概率波的艺术

量子编程的本质，是精确操控量子态的演化，通过干涉效应放大正确答案，湮灭错误答案。

• 相长干涉 vs. 相消干涉：如同水波，当两个概率幅的波峰相遇，则相互增强（相长干涉）；波峰遇波谷则相互抵消（相消干涉）。量子算法就是精心设计的"编舞"，让代表错误答案的路径相互抵消，让正确答案的路径同步增强。

• 为何需要深厚数学 ：这个过程远非"波峰波谷"这么简单。它需要在由复数 和线性代数 构建的希尔伯特空间 中进行。量子态是向量，量子门是矩阵（酉矩阵），算法是矩阵的连乘。设计Shor算法需要数论 和群论来提取周期；理解Grover算法需要几何直观来分析状态空间的旋转。没有深厚的数学功底，就无法设计出这种巧妙的干涉模式。

量子编程的实现流程：

1. 算法设计：数学家构思如何将问题（如质因数分解）转化为量子态的干涉过程。

2. 编写代码 ：程序员使用Qiskit 、Cirq 或Q# 等高级框架描述量子电路（定义量子比特、应用量子门）。

3. 编译与转换 ：编译器将高级电路分解为量子硬件支持的原生门集，并优化电路以适应硬件的物理连接（拓扑结构），最终将其转换为一系列控制脉冲。

4. 执行与测量：脉冲被发送到量子处理器，操控量子比特执行计算。最后，测量使量子态坍缩，得到经典比特串。由于概率特性，电路需运行成千上万次，再对结果进行统计分析才能得出答案。

三、硬件实现：在极端条件下驾驭量子

理论上的瑰丽需要坚实的物理载体。当前主流的技术路径包括：

• 超导回路：在芯片上制作微型超导线圈，用电流方向表示0和1。通过在极低温（接近绝对零度）下施加微波脉冲进行操控。这是IBM、Google采用的方案。

• 离子阱：将单个原子离子悬浮在真空腔中，用激光脉冲操控其电子能级。操控精度高，相干时间长。

• 光子：利用光子的偏振或路径编码信息，通过分束器、相位调制器等光学元件进行操控。可在室温下运行。

所有这些平台都面临巨大挑战：退相干 （脆弱的量子态极易被环境破坏）和误差 。因此，当前处于 "含噪声中等规模量子"（NISQ） 时代，量子计算机通常与经典计算机协同工作，处理特定子任务。

四、材料科学：量子革命的基石

量子计算机的性能天花板，最终由量子材料决定。这个专业致力于研究和发现那些能展现出奇异量子效应的物质，例如：

• 高温超导体：寻找更高温度下零电阻导电的材料，是构建能耗更低、更易维护的量子计算机的关键。

• 拓扑材料 ：具有表面导电、体内绝缘的奇异特性，其拓扑保护状态极其稳定，是实现高容错拓扑量子计算的理想选择。

• 二维材料：如石墨烯，为构建新型量子器件和异质结提供了"原子乐高"。

五、应用与未来：并非万能，但变革性的

量子计算机并非万能。它不适合处理简单算术、文字编辑或I/O密集型任务。它的优势在于解决具有特定结构的问题：

• 密码学：Shor算法能破解RSA加密，迫使世界发展抗量子密码。

• 药物与材料设计：精确模拟分子和材料的量子行为，加速新药和新能源材料的研发。

• 优化问题：为物流、金融建模等复杂优化问题提供更优解。

• 人工智能：加速机器学习中的线性代数运算。

结论

量子计算是一场深刻的跨学科革命。它要求：

• 数学家设计巧妙的算法；

• 计算机科学家构建编程栈和编译器；

• 物理学家和工程师造出稳定可靠的硬件；

• 材料科学家提供性能更优的量子比特载体。

从抽象的复数方程到极低温下的微波脉冲，量子计算的故事是人类试图理解并驾驭自然界最深层规律，并将其转化为强大技术力量的伟大尝试。它预示着一个新时代的曙光，其中计算的概念将被彻底重塑。

当然可以。量子计算机的编程是一个激动人心且快速发展的领域，它融合了量子物理、计算机科学和数学。我会用一个从抽象到具体的方式，为您详细解释它是如何实现的。

核心思想：与传统编程的根本不同

首先，最关键的是要理解量子编程和经典（传统）编程的哲学差异：

1. 经典编程 ：处理的是比特（Bit），它要么是0，要么是1。程序的状态在任何时刻都是确定的。

2. 量子编程 ：处理的是量子比特（Qubit）。一个量子比特可以同时是0和1的叠加态（Superposition）。多个量子比特之间还可以形成"纠缠"（Entanglement）这种神奇的关联。

因此，量子编程的本质是：操纵处于叠加和纠缠状态的量子比特系统，通过量子门序列构建一个特定的量子态，最后通过测量将这个量子态的概率分布转化为我们需要的答案。

---

量子编程的流程（如何实现）

量子编程的实现可以概括为以下四个关键步骤，下图清晰地展示了这一流程：

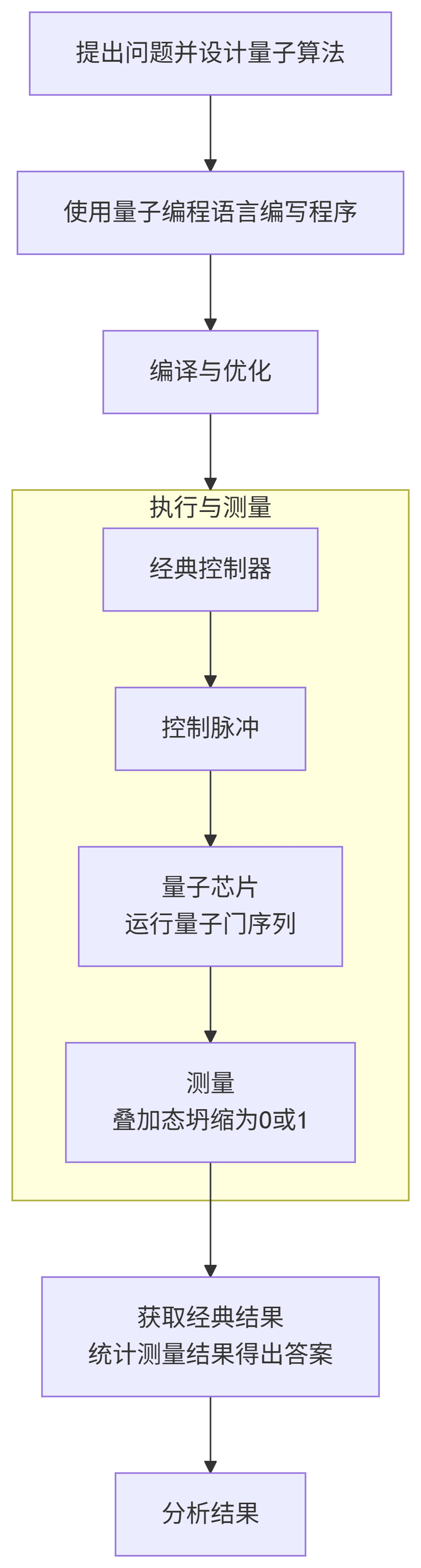
flowchart TD
    A[提出问题并设计量子算法] --> B[使用量子编程语言编写程序]
    B --> C[编译与优化]
    C --> D[在量子处理器上执行]
    subgraph D [执行与测量]
        D1[经典控制器] --> D2[控制脉冲]
        D2 --> D3[量子芯片<br>运行量子门序列]
        D3 --> D4[测量<br>叠加态坍缩为0或1]
    end
    D4 --> E[获取经典结果<br>统计测量结果得出答案]
    E --> F[分析结果]

下面我们来详细解读每一个步骤。

第1步：算法设计与建模（在脑海中）

这是最困难的一步，需要数学家和高阶量子程序员的智慧。目标是找到一个量子算法，使其在解决问题的速度上远超最好的经典算法。

• 经典例子：

  • Shor算法：用于大数质因数分解，能破解广泛使用的RSA加密。

  • Grover算法：用于无序数据库搜索，提供平方级的加速。

• 做法 ：程序员需要将问题转化为一个量子态的准备和变换过程。他们利用叠加和纠缠的特性，让量子计算机同时探索无数种可能性，并通过干涉（Interference）放大正确答案的概率，同时减小错误答案的概率。

第2步：编写量子程序（在电脑上）

程序员使用量子编程语言和框架来"描述"第1步中设计的量子电路（操作序列）。

这些语言看起来和Python等经典语言很像，因为它们运行在经典计算机上，用于"描述"量子电路。

• 主流量子编程框架：

  • Qiskit (IBM)：基于Python的框架，是目前最流行的之一。

  • Cirq (Google)：基于Python，专注于为特定量子处理器设计电路。

  • Q# (Microsoft)：一门独立的量子编程语言，与Visual Studio深度集成。

  • PennyLane (Xanadu)：一个专注于"量子机器学习"的框架，支持多种硬件后端。

• 代码示例（使用Qiskit）：创建一个简单的量子电路，生成一个量子比特的叠加态。

python

# 这是一个在经典电脑上运行的Python代码，它“描述”了一个量子程序
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram

# 创建一个量子电路：1个量子比特，1个经典比特（用于存储测量结果）
qc = QuantumCircuit(1, 1)

# 在量子比特上施加操作（量子门）：
qc.h(0)  # 施加哈德玛门（Hadamard gate），将量子比特从 |0> 变为 |0> + |1> 的叠加态
qc.measure(0, 0) # 测量这个量子比特，结果存入经典比特

# 选择一个模拟器后端（用经典电脑模拟量子计算机）
simulator = AerSimulator()

# 编译电路以适应后端
compiled_circuit = transpile(qc, simulator)

# 运行电路1000次（1000次“射击”）
job = simulator.run(compiled_circuit, shots=1000)

# 获取结果
result = job.result()
counts = result.get_counts()

# 可视化结果：应该看到‘0’和‘1’的出现概率各约50%
print(counts)
# 输出类似: {'0': 512, '1': 488}

第3步：编译与转换

编写好的高级代码不能被量子处理器直接理解。它需要被编译和转换：

1. Transpilation（转换） ：将高级量子门操作分解为当前量子计算机硬件支持的原生门集合（Native Gates） 。就像经典CPU只支持加法、移位等基本指令一样，量子芯片也只支持有限的一组基本量子门（如CNOT, RZ, SX等）。

2. 优化 ：编译器会优化电路，比如减少门的数量、调整门顺序以适应硬件的物理连接（量子比特拓扑结构），以最大限度地降低错误率。

3. 生成控制指令 ：最终，编译后的量子电路被转换成一连串极其精确的微波激光脉冲 或磁脉冲信号。这些脉冲就是实际去驱动量子比特，执行量子门操作的"机器代码"。

第4步：执行与测量

1. 发送至控制系统 ：编译后的脉冲指令被发送到量子计算机的经典控制系统。

2. 操控量子比特 ：这个经典控制系统产生相应的微波或电压脉冲，通过线路传输到低温恒温器（Dilution Refrigerator）中，施加在量子处理器（QPU） 的量子比特上。

3. 测量 ：在电路的最后，程序会发出测量指令。测量会使量子比特的叠加态坍缩（Collapse） 到一个确定的经典状态（0或1）。

4. 读取结果 ：测量结果（一串0和1的经典比特）被传回经典计算机。由于量子概率的特性，一个量子电路通常需要运行成千上万次 （称为shots），然后对所有这些结果进行统计分析，才能得到最终答案的概率分布。

---

当前量子编程的挑战

• 噪音与错误：目前的量子计算机是"含噪音的中型量子（NISQ）"设备。量子比特非常脆弱，容易受到环境干扰而出错（退相干）。编程时必须考虑这些错误。

• 纠错 ：大规模应用需要量子纠错（QEC），但这需要大量额外的量子比特来编码一个"逻辑量子比特"，目前技术尚未成熟。

• 混合编程 ：量子计算机不会取代经典计算机，而是协同工作。通常的模式是：经典计算机运行主程序，遇到需要大量并行计算的任务时，将其卸载（Offload） 到量子计算机上执行，量子计算机返回结果后再由经典计算机继续处理。

总结

量子计算机的编程实现是一个分层结构：

1. 应用层：用Qiskit/Cirq/Q#等高级框架编写算法。

2. 编译层：将算法编译优化成硬件相关的低级脉冲指令。

3. 控制层：经典控制系统将脉冲指令转换为物理信号。

4. 物理层：物理信号操控真实的量子设备（量子处理器）执行计算并测量。

简单来说，量子编程就是设计一个利用叠加和纠缠的电路，通过编译将其转化为控制量子比特的脉冲序列，最终通过大量测量和统计，从概率中获取答案的过程。 它要求程序员既要有计算机科学的思维，也要对量子力学有直观的理解。

这是一个非常深刻和关键的问题。答案可以概括为：

是的，但需要极其重要的补充和澄清。 量子计算机的优势确实来自于一种独特的"并行性"，但它并非 传统意义上"同时做多件事"的并行计算，而且这种能力也并非适用于所有问题。

下面我们来详细解释"为什么"。

核心：量子并行性（Quantum Parallelism）的本质

量子计算机的能力核心是量子并行性。这源于量子比特的叠加态。

• 经典情况 ：一个由3个经典比特组成的内存，一次只能存储一个 值（例如 101）。

• 量子情况 ：一个由3个量子比特组成的寄存器，由于叠加态，可以同时存储 2\^3 = 8 种可能组合（000, 001, 010, ..., 111）的叠加。

如果你对一个量子寄存器施加一个操作（例如一个函数计算 f(x)），那么这个操作会同时作用于所有可能的输入上。在某种意义上，你只进行了一次计算，但却得到了 2\^n 个结果。

但这引出了一个关键问题： 如果你试图直接读取所有这些结果，量子叠加态会坍缩，你只会随机得到其中一个结果，而失去了所有其他信息。这就像做了一场丰富多彩的梦，醒来的一瞬间只记得一个片段。

真正的魔力：干涉（Interference）

如果量子并行性只是"同时计算，但无法读取"，那它就毫无用处。量子算法的精髓在于在测量之前，巧妙地操纵这些叠加态。

1. 并行计算：在一次操作中，同时对所有可能的输入进行计算，将结果编码在一个巨大的叠加态中。

2. 精心设计操作 ：通过一系列精心设计的量子门（操作），让代表错误答案 的路径相互抵消（相消干涉 ），而让代表正确答案 的路径相互增强（相长干涉）。

3. 测量 ：最后进行测量。此时，由于干涉效应，叠加态坍缩到正确答案的概率被最大化，而错误答案的概率被最小化。

所以，量子计算机不是在"同时计算所有答案然后挑出对的"，而是在"同时利用所有可能性来创造一个高概率输出正确答案的最终状态"。

一个完美的比喻：

想象你在一片漆黑中迷路了，只有一条手电筒（经典计算机），你只能一次一条路地尝试。

而量子计算机就像你突然拥有了无数个手电筒，同时照亮了所有路径。但关键不是你同时看到了所有路，而是你拥有一种特殊的滤镜（干涉），可以立刻让那条正确的路变得最亮，而其他错误的路径都变暗，这样你一眼就能看出该往哪走。

---

为什么量子优势不是万能的？

正是因为需要这种"干涉"步骤，使得量子计算机并非对所有问题都有效。它非常适合的问题通常具有以下特征：

1. 问题本身具有内在的并行结构：算法的核心步骤可以转化为对一个函数的评估，而这个函数需要处理海量的潜在输入。Shor算法（分解质因数）和Grover算法（搜索）都是完美的例子。

2. 存在巧妙的数学技巧：科学家们必须找到一种方法，能够为特定问题设计出引发"相长干涉"和"相消干涉"的量子门序列。这是一个极其困难的过程，需要深厚的数学功底。这也是为什么目前真正展现出量子优势的算法屈指可数。

哪些问题适合/不适合量子计算机？

✅ 适合的问题（可能具有量子优势）：

• 因数分解（Shor算法）：破解RSA加密的基础，经典计算机极难完成，量子计算机可高效解决。

• 无序数据库搜索（Grover算法）：提供平方加速，例如从N个条目中搜索目标，仅需 ~\\sqrt{N} 次操作。

• 量子化学模拟：模拟分子和材料的量子行为。因为模拟对象本身就是量子系统，用经典计算机模拟指数困难，而量子计算机是"自然模拟器"。

• 优化问题：在某些组合优化问题上（如旅行商问题），量子退火器等特定类型的量子计算机可能找到更好的近似解。

• 机器学习：加速某些线性代数运算，如矩阵求逆、特征值计算，从而加速机器学习训练过程。

❌ 不适合的问题（经典计算机更好）：

• 简单的算术计算：如加减乘除、处理Excel表格、运行Word程序。这些任务没有并行结构，经典计算机的专用硬件处理得更快。

• 大部分逻辑控制任务：操作系统的调度、网络通信、人机交互等。

• 输入输出（I/O）密集型任务：读写硬盘、显示图形等，这些任务的瓶颈在于物理设备的速度，而非计算本身。

• 没有高效量子算法的问题：对于许多问题，至今尚未找到能利用量子并行性和干涉来提供加速的算法。对于这些问题，量子计算机甚至可能比经典计算机更慢。

总结

所以，回到你的问题：

量子计算机是只适合大量并行计算吗？为什么？

• 是 ，它的巨大潜力确实来自于其利用量子并行性同时处理指数级数量可能性的独特能力。

• 但更是 ，它的成功高度依赖 于能否为特定问题设计出利用量子干涉来放大正确答案的算法。没有干涉，并行性就毫无用处。

• 因此，它是一种专用型 而非通用型的计算范式。它不会取代经典计算机，而是将与经典计算机协同工作，专门用于解决那些具有特定结构、经典计算机难以处理的复杂问题。

非常好，这是一个触及核心的问题。量子计算机的实现是一个跨越多个层次的宏大工程，从抽象的数学算法一直到具体的物理操控。它是一场自上而下 的设计与自下而上的构建的结合。

下图清晰地展示了实现量子计算机所涉及的四个核心层级：

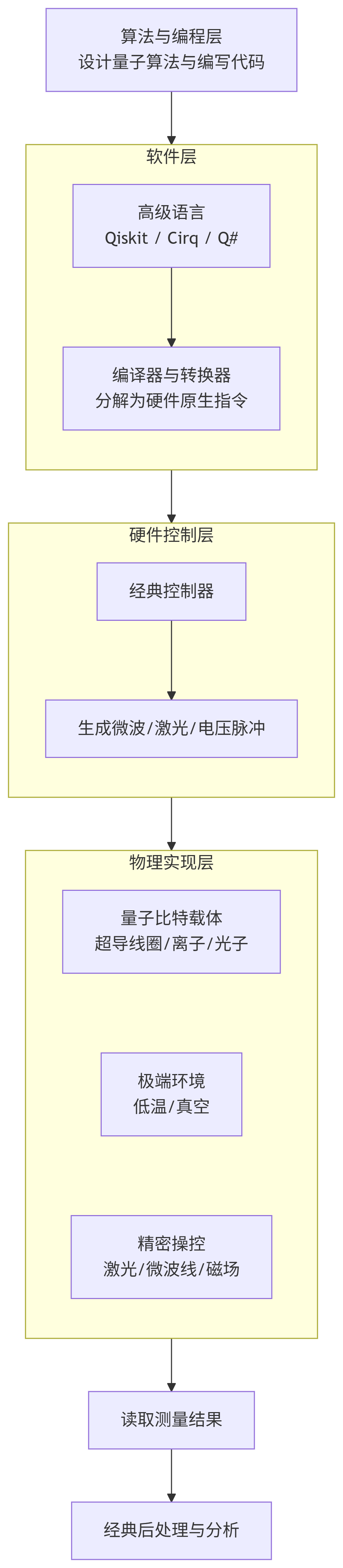
flowchart TD
    A[算法与编程层<br>设计量子算法与编写代码] --> B

    subgraph B [软件层]
        B1[高级语言<br>Qiskit / Cirq / Q#]
        B1 --> B2[编译器与转换器<br>分解为硬件原生指令]
    end

    B --> C

    subgraph C [硬件控制层]
        C1[经典控制器]
        C1 --> C2[生成微波/激光/电压脉冲]
    end

    C --> D

    subgraph D [物理实现层]
        D1[量子比特载体<br>超导线圈/离子/光子]
        D2[极端环境<br>低温/真空]
        D3[精密操控<br>激光/微波线/磁场]
        
        D1 ~~~ D2 ~~~ D3
    end

    D --> E[读取测量结果]
    E --> F[经典后处理与分析]

下面，我们自底向上，从最基础的物理层开始，详细解读每个层级是如何实现的。

---

层级 1：物理实现层（如何制造和操控一个量子比特）

这是最底层的工程挑战，核心是找到一种可控的物理系统来表征量子比特（Qubit）。一个理想的量子比特需要满足几个苛刻条件：长相干时间（能维持叠加态）、高保真度（操作准确）、可扩展性（能集成大量比特）和可读取性（能测量）。

目前主流的物理实现方案有：

1. 超导回路（Superconducting Circuits） - IBM, Google 采用

   • 如何实现：在芯片上制作微小的超导金属（如铌）回路。利用超导状态下电子无阻流动的特性，形成两个不同的量子能级（如电流顺时针/逆时针流动）来代表 |0> 和 |1>。

   • 如何操控 ：通过精准的微波脉冲（发送到连接量子比特的微波线）来操纵量子态，实现量子门操作。比特之间通过电容或电感耦合。

   • 挑战 ：极易受环境热噪声干扰，必须在接近绝对零度（-273°C）的极低温稀释冰箱中运行。

2. 离子阱（Trapped Ions） - IonQ, Honeywell 采用

   • 如何实现：将单个原子（如镱、钙原子）离子化，并用电磁场将其悬浮在真空腔中。利用原子自身稳定的电子能级作为 |0> 和 |1>。

   • 如何操控 ：用精确的激光脉冲照射离子，驱动其电子能级跃迁，从而实现量子门操作。离子之间的相互作用通过它们的集体运动（声子）来实现，形成纠缠。

   • 挑战：操控精度高，相干时间长，但系统复杂，扩展较慢。

3. 光子（Photonics） - Xanadu 等采用

   • 如何实现：利用光子的不同自由度来编码量子信息，如偏振（水平偏振为 |0>，垂直偏振为 |1>）、路径或轨道角动量。

   • 如何操控 ：使用分束器、相位调制器和非线性晶体等光学元件来操纵光子，实现量子门。纠缠通过特殊晶体的"参量下转换"过程产生。

   • 挑战：通常在室温下运行，但制造高品质的光子源和进行大规模集成是巨大挑战。

---

层级 2：硬件控制层（如何将指令变为物理信号）

这一层是连接软件和硬件的桥梁，负责将编译好的量子指令（门序列）转换成控制物理设备的模拟信号。

1. 编译输出 ：软件层输出的是一系列定时、定频、定幅的脉冲序列描述。

2. 经典控制器：一组精密的电子设备（如任意波形发生器AWG）。它们读取脉冲描述。

3. 生成信号 ：控制器产生相应的微波脉冲 （对于超导比特）或激光脉冲（对于离子阱）。

4. 信号传输：这些脉冲通过电缆或光纤被传输到低温或真空环境中，精确地施加在目标量子比特上。

一个关键概念：原生门 (Native Gates)

硬件层不能直接理解"哈达玛门"或"CNOT门"这种抽象概念。每个物理平台都有一组硬件直接支持的基本操作，即"原生门集"。编译器的任务之一就是将高级量子电路分解成这些原生门的序列。

---

层级 3：软件层（如何让人能"编程"）

这一层让我们能够用人类可理解的方式描述量子算法。

1. 量子编程语言和框架：如 Qiskit (Python库)、Cirq (Python库)、Q# (独立语言)。程序员用它们来定义量子比特、施加量子门、指定测量方式。

2. 编译器（Compiler）和转换器（Transpiler）：

   • 语法检查与优化：就像经典编译器一样，首先进行基础检查。

   • 电路分解：将程序员使用的高层级量子门分解为硬件支持的原生门集合。

   • 量子比特映射与路由 ：这是量子编译独有的挑战。由于硬件上并非所有量子比特都直接相连，当需要执行一个在两个不相邻比特上的操作（如CNOT门）时，编译器必须智能地插入SWAP操作来交换量子比特的状态，从而将它们"路由"到可以相互作用的位置。这个过程极大地影响电路的最终性能和错误率。

---

层级 4：算法与应用层（如何解决实际问题）

这是最顶层，决定了我们为什么要建造量子计算机。

1. 设计量子算法：数学家和高阶程序员设计出能利用量子并行性和干涉的算法，如Shor算法、Grover算法、量子相位估计等。

2. 混合编程模型 ：在目前所谓的NISQ（含噪声中等规模量子）时代，量子计算机并非独立工作。最常见的模式是：

   • 经典CPU运行主程序。

   • 当遇到适合量子计算的子任务时（例如计算一个分子的基态能量），经典CPU调用量子处理器。

   • 量子处理器执行编译好的量子电路，进行多次测量后，将结果的统计分布（一堆0和1的计数）返回给经典CPU。

   • 经典CPU再基于这个结果进行后续处理。

3. 错误缓解 ：由于当前量子比特容易出错，软件层还需要采用高级的错误缓解技术，通过多次运行特殊设计的电路来估计噪声的影响，并从带噪声的结果中推断出更接近真实值的答案。

总结：一次完整的计算是如何实现的？

以一个简单的"抛量子硬币"程序为例，它综合了以上所有层级：

1. 应用层：你想生成一个随机数。

2. 软件层：你用Qiskit写了两行代码：创建一个量子比特，对它加一个H门（哈达玛门），然后测量。

3. 编译层：Qiskit编译器知道目标硬件是IBM的超导芯片，它将H门分解为该芯片原生门集（如特定的微波脉冲序列）。

4. 控制层：经典控制器根据编译结果，生成一个特定时长、频率和幅度的微波脉冲。

5. 物理层：这个微波脉冲被送入稀释冰箱，施加在目标超导量子比特上，使其进入 |0> 和 |1> 的叠加态。

6. 测量 ：一个测量脉冲被发出，导致量子比特的叠加态坍缩为一个确定的经典状态（比如0）。

7. 读取：测量结果（0）被传回经典控制器，再传回你的经典程序。

8. 重复：你的程序命令这个流程重复了1000次，得到了大约500个0和500个1，从而验证了量子随机性。

因此，量子计算机的实现是数学、计算机科学、电子工程和量子物理的极致融合，是人类工程学上的一个奇迹。

好的，这是一个非常前沿且重要的专业。量子材料专业 是凝聚态物理的一个核心分支，它主要研究那些无法用经典物理理论解释、其性质由量子力学效应主导的新奇材料。

简单来说，它研究的不是材料的常规特性（比如多硬、多导电），而是当材料在极端条件（如极低温、强磁场）下或具有特殊结构时，其内部的电子行为所展现出的集体量子现象。

我们可以从以下几个核心方面来理解这个专业：

---

一、核心研究目标：探索和利用"宏观量子现象"

经典物理认为，量子效应（如叠加、纠缠）通常只在微观尺度（原子、分子）下显现，一旦放大到宏观世界就会消失。但量子材料颠覆了这一认知。它研究的正是那些在宏观尺度上也能观察到惊人量子效应的材料。

二、主要研究对象（几个关键方向）

量子材料包含许多具体的分类，每一种都对应着奇特的物理现象：

1. 超导体（Superconductors）

   • 研究什么：研究为何这些材料在低于特定温度时，电阻会突然降为零（完全导电），并且会完全排斥磁场（迈斯纳效应）。

   • 为什么是"量子"的：超导的本质是电子结成"库珀对"，这是一种宏观的量子纠缠态，所有电子对协同运动，表现出单一的量子波函数。

   • 目标：寻找在更高温度（甚至室温）下工作的超导体，这将引发能源、交通（磁悬浮）、医疗（MRI）等领域的革命。

2. 拓扑材料（Topological Materials）

   • 研究什么：研究材料的电子能带结构所具有的"拓扑"性质。拓扑是一个数学概念，描述物体在连续变形下不变的属性（如甜甜圈和咖啡杯都有一个洞，拓扑等价）。

   • 为什么是"量子"的：拓扑序是一种全局的量子性质。这导致了非常奇特的现象，比如：

     • 拓扑绝缘体：材料内部是绝缘体，但其表面却是完美的导体，并且表面电流不会被缺陷散射（极其稳定）。

     • 目标：应用于未来低能耗电子学和量子计算，因为拓扑保护的状态非常稳定，不易退相干。

3. 二维材料及其异质结（2D Materials & Heterostructures）

   • 研究什么：研究像石墨烯（单层碳原子）、二硫化钼等只有一个或几个原子层厚度的材料。更重要的是，像搭乐高一样，将不同的二维材料堆叠在一起形成"范德瓦尔斯异质结"。

   • 为什么是"量子"的：在二维极限下，电子的运动被限制在平面内，量子限域效应变得极其显著。通过不同材料的堆叠，可以人工设计和创造出自然界不存在的全新量子态。

4. 强关联电子系统（Strongly Correlated Electron Systems）

   • 研究什么：研究电子之间存在强烈相互作用的材料。在传统材料中，电子近似独立运动；但在强关联体系中，电子"彼此牵制"，行动高度协同。

   • 例子：高温超导体、重费米子体系、量子自旋液体等。这些材料通常具有非常丰富的相图，随温度、压力、磁场变化而出现截然不同的性质。

   • 目标：理解电子间复杂的相互作用，从而发现新的量子相和现象。

5. 量子磁体（Quantum Magnets）

   • 研究什么：研究磁性的量子根源。在原子尺度上，磁性源于电子的自旋。量子磁体研究这些自旋如何通过量子力学效应相互作用和有序排列。

   • 为什么是"量子"的：即使在绝对零度，由于量子涨落，自旋也可能无法形成经典的有序态，从而形成"量子自旋液体"等 exotic 状态，其中可能孕育着拓扑序和任意子（Anyons）等用于量子计算的概念。

三、研究手段和方法

量子材料的研究是高度交叉的，结合了：

• 理论：发展新的理论模型和计算物理方法（如密度泛函理论DFT、动力学平均场理论DMFT）来预测和解释实验现象。

• 实验：

  • 材料合成：生长高质量的单晶样品、制备薄膜和异质结。

  • 极端条件：在极低温（mK级别）、强磁场、高压条件下测量材料的电学、磁学、热学性质。

  • 尖端表征：利用同步辐射、中子散射、扫描隧道显微镜（STM）、角分辨光电子能谱（ARPES）等大型科学装置来探测材料的原子结构和电子结构。

四、为什么这个专业如此重要？（应用前景）

• 下一代信息技术：为拓扑量子计算等革命性计算范式提供物理载体。

• 能源革命：零能耗输电线（超导）、高效能源转换器件。

• 新型传感器：基于量子干涉效应的超灵敏磁传感器（SQUID），已用于脑磁图、资源勘探等。

• 基础科学突破：不断发现新的物态和物理规律，深化我们对复杂量子多体系统的理解。

总结

量子材料专业的核心，是探索、设计、制备和研究那些具有新颖电子态、其宏观性质由量子力学效应主导的材料。它不仅是基础物理的前沿，更肩负着为未来技术革命提供物质基础的使命。

如果你选择这个专业，你将处于物理学、材料科学、化学和工程学的交叉点，致力于理解并最终驾驭自然界最深层次的规律来创造新材料。

说相长干涉和相消干涉需要深厚的数学功底，并不是指理解"波峰波谷叠加"这个基本概念本身有多难，而是指要在复杂的量子系统中精确地设计、预测和控制这些干涉效应，以实现特定的计算目标，这背后需要极其强大和深刻的数学工具。

我们可以从一个简单的类比开始，逐步深入：

1. 直观理解（不需要高深数学）：

   • 相长干涉：就像两个声波同步，声音变大。

   • 相消干涉：就像降噪耳机，产生反向声波抵消噪音。

   • 在量子世界里，这就是波函数（描述粒子概率幅的波）的叠加。

2. 为什么这变得复杂（需要数学了） ：

   量子计算不是两个波，而是2ⁿ个波 （n个量子比特就有2ⁿ个基态）的叠加。你的操作（量子门）会同时影响所有波的相位。你的目标不是简单地让一个波变大，而是让所有错误答案路径的波精确地 相互抵消（相消干涉），同时让所有正确答案路径的波精确地相互增强（相长干涉）。

这个过程需要深厚数学功底的原因体现在以下几个层面：

---

1. 描述工具：复数、线性代数和希尔伯特空间

• 概率幅是复数 ：在量子力学中，一个量子态的概率幅（Amplitude）不是常规的概率（实数），而是复数 。它有模长（决定概率）和相位（Phase）。干涉的核心就是操控相位。

  • 相长干涉：相位相同的复数相加，模长增大。(1 + 1 = 2)

  • 相消干涉：相位相反的复数相加，模长相消。(1 + (-1) = 0)

  • 没有复数的数学，就无法准确描述量子态的本质。

• 量子态是向量，操作是矩阵 ：一个多量子比特系统的状态存在于一个高维的希尔伯特空间 中，可以表示为一个巨大的向量（例如，|00⟩, |01⟩, |10⟩, |11⟩ 是4维空间的一组基）。量子门操作（如哈达玛门、CNOT门）则是作用在这个向量上的酉矩阵。

  • 设计量子算法，本质上就是在设计一系列酉矩阵的连乘，使得初始状态向量（如 |00...0⟩）被变换成一个精心设计的最终状态向量，其中正确答案的概率幅最大。

  • 没有线性代数和矩阵理论，就无法理解和描述量子系统的演化。

2. 算法设计：群论、数论和抽象代数

这是最需要"深厚功底"的地方。如何找到那组正确的矩阵（量子门序列）来解决问题？

• Shor算法（质因数分解）：

  • 它的核心是利用量子并行性计算一个函数的所有值，然后通过量子傅里叶变换找到函数的周期。

  • 量子傅里叶变换是算法的关键步骤，它本质上是一次巨大的相干操作，能够极其高效地提取出周期信息。它让不同路径的波以其相位相互干涉，只有在特定周期处发生相长干涉，其他地方全部相消。

  • 理解为什么量子傅里叶变换能 work，以及如何将它映射到质因数分解问题上，需要数论 （寻找周期）和群论（傅里叶变换在循环群上的应用）的知识。这远远超出了简单的波叠加概念。

• Grover算法（无序搜索）：

  • 它通过反复应用一个"Oracle"（标记答案）和一个"扩散算子"（放大振幅差）来实现平方加速。

  • 这个过程可以巧妙地理解为在二维平面上旋转状态向量。每一次迭代都将答案状态的振幅放大一点，非答案状态的振幅缩小一点。

  • 要证明这个算法确实以高概率找到答案，需要精确计算每次旋转的角度，这需要几何 和振幅放大的数学理论。

3. 性能分析与容错：概率论和复杂理论

• 输出是概率性的：量子计算的结果是概率分布。你需要运行多次并统计结果。数学功底用于分析：需要运行多少次才能以足够高的置信度得到正确答案？算法的成功概率是多少？

• 复杂性分析 ：数学家需要证明一个新算法相比经典算法是否有真正的优势（如Grover的√N次 vs 经典N次）。这属于计算复杂性理论的范畴，需要严格的数学证明，而不仅仅是实验验证。

• 纠错与容错 ：由于量子系统极其脆弱，需要引入量子纠错码。这些纠错码的设计（如表面码）和阈值定理的证明，依赖于拓扑学 和随机化等高级数学工具。

总结：从"是什么"到"怎么做"和"为什么"

• 科普层面 ：理解相长/相消干涉"是什么" -> 需要初等物理概念。

• 工程师层面 ：使用现成的量子门"实现"一个已知算法 -> 需要线性代数 和编程技能。

• 科学家层面 ："设计"一个新的量子算法，"证明"其优越性，"优化"其性能 -> 需要深厚的数学功底（包括但不限于复分析、线性代数、群论、数论、概率论、复杂理论）。

因此，深厚的数学功底是探索量子计算未知领域的"语言"和"地图"。 它让研究人员能够：

1. 精确描述复杂的量子系统和操作。

2. 抽象建模，将现实问题转化为可计算的量子电路。

3. 设计巧妙的干涉模式，而不仅仅是盲目的试错。

4. 严格证明算法的正确性和效率。

没有这些数学工具，量子计算将停留在哲学思辨和简单演示的阶段，无法发展成为一门精确的工程科学。