两数相加
1. 题目描述
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
ini
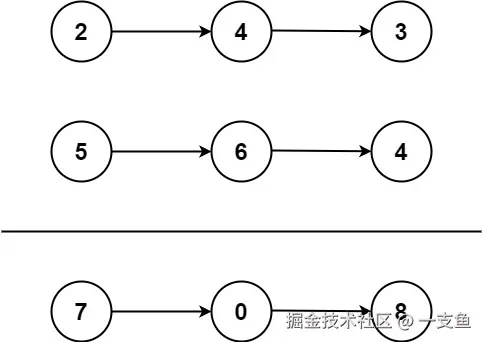
输入: l1 = [2,4,3], l2 = [5,6,4]
输出: [7,0,8]
解释: 342 + 465 = 807.示例 2:
css
输入: l1 = [0], l2 = [0]
输出: [0]示例 3:
css
输入: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出: [8,9,9,9,0,0,0,1]提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
2. 解决方案
1. 常规链表遍历解法
- 思路:
- 同时遍历两个链表,从表头开始,将对应节点的值相加,并考虑进位。
- 创建一个新的链表来存储相加的结果。
- 遍历过程中,如果一个链表先遍历完,另一个链表剩余部分继续参与计算,同时处理进位情况直到所有节点遍历完且没有进位。
- 代码实现:
ts
// 定义链表节点类
class ListNode {
val: number;
next: ListNode | null;
constructor(val?: number, next?: ListNode | null) {
this.val = (val === undefined? 0 : val);
this.next = (next === undefined? null : next);
}
}
function addTwoNumbers(l1: ListNode | null, l2: ListNode | null): ListNode | null {
let dummyHead = new ListNode();
let p = l1, q = l2, current = dummyHead;
let carry = 0;
while (p!== null || q!== null) {
let x = p? p.val : 0;
let y = q? q.val : 0;
let sum = carry + x + y;
carry = Math.floor(sum / 10);
current.next = new ListNode(sum % 10);
current = current.next;
if (p) p = p.next;
if (q) q = q.next;
}
if (carry > 0) {
current.next = new ListNode(carry);
}
return dummyHead.next;
}- 分析:
- 时间复杂度:(O(max(m, n))),其中 m 和 n 分别是两个链表的长度。因为我们需要遍历两个链表的最长者。
- 空间复杂度:(O(max(m, n))),新链表的长度最大为较长链表的长度加 1(考虑进位)。
- 优点:
- 思路直接明了,易于理解和实现。按照链表相加的实际逻辑进行处理,符合人类计算加法的思维方式。
- 缺点:
- 没有对链表的遍历和计算过程进行特殊优化,对于非常长的链表,可能在性能上存在一定瓶颈。
2. 递归解法
- 思路:
- 递归地处理链表节点的相加。每次递归处理当前两个节点的和以及进位。
- 递归的终止条件是两个链表都为空且没有进位。
- 代码实现:
ts
function addTwoNumbersRecursive(l1: ListNode | null, l2: ListNode | null, carry = 0): ListNode | null {
if (!l1 &&!l2 &&!carry) {
return null;
}
let sum = carry;
sum += l1? l1.val : 0;
sum += l2? l2.val : 0;
let newNode = new ListNode(sum % 10);
newNode.next = addTwoNumbersRecursive(
l1 && l1.next,
l2 && l2.next,
Math.floor(sum / 10)
);
return newNode;
}- 分析:
- 时间复杂度:(O(max(m, n))),同样需要遍历两个链表的最长者。
- 空间复杂度:(O(max(m, n))),递归调用栈的深度最大为较长链表的长度加 1(考虑进位)。
- 优点:
- 代码简洁,递归的方式能够很好地体现链表结构的递归特性,使代码更具逻辑性和可读性。
- 缺点:
- 递归调用会消耗额外的栈空间,对于非常长的链表,可能导致栈溢出问题。相比迭代解法,性能上在某些情况下可能稍逊一筹。
3. 最优解及原因
- 最优解:常规链表遍历(迭代)解法是更优选择。
- 原因:虽然两种解法时间复杂度相同,但迭代解法在空间使用上更为稳定,不会因为递归调用而产生栈溢出风险,尤其是在处理非常长的链表时,迭代解法更加可靠。
3.拓展和题目变形
拓展
- 如果链表中的数字是正序存储(即最高位在链表头部),如何解决?
思路:
- 一种方法是先将链表反转,然后按照现有方式相加,最后再将结果链表反转。
- 另一种更高效的方法是使用栈来存储链表节点的值,因为栈可以实现后进先出,从而模拟逆序相加的过程。
代码实现(使用栈) :
ts
function addTwoNumbersForward(l1: ListNode | null, l2: ListNode | null): ListNode | null {
let stack1: number[] = [];
let stack2: number[] = [];
while (l1) {
stack1.push(l1.val);
l1 = l1.next;
}
while (l2) {
stack2.push(l2.val);
l2 = l2.next;
}
let carry = 0;
let result: ListNode | null = null;
while (stack1.length > 0 || stack2.length > 0 || carry > 0) {
let sum = carry;
sum += stack1.length > 0? stack1.pop()! : 0;
sum += stack2.length > 0? stack2.pop()! : 0;
carry = Math.floor(sum / 10);
let newNode = new ListNode(sum % 10);
newNode.next = result;
result = newNode;
}
return result;
}题目变形:
- 如果链表中的节点值可以是负数,如何处理?
思路:
- 在计算节点值之和时,直接按照整数运算规则处理负数。
- 处理进位时需要注意,当和为负数时,需要将进位调整为 -1,同时节点值加上 10(例如 -2 可表示为 -1 进位和 8 节点值)。
代码实现:
ts
function addTwoNumbersWithNegative(l1: ListNode | null, l2: ListNode | null): ListNode | null {
let dummyHead = new ListNode();
let p = l1, q = l2, current = dummyHead;
let carry = 0;
while (p!== null || q!== null) {
let x = p? p.val : 0;
let y = q? q.val : 0;
let sum = carry + x + y;
if (sum < 0) {
carry = -1;
sum += 10;
} else {
carry = Math.floor(sum / 10);
}
current.next = new ListNode(sum % 10);
current = current.next;
if (p) p = p.next;
if (q) q = q.next;
}
if (carry!== 0) {
current.next = new ListNode(carry);
}
return dummyHead.next;
}