亲手算一遍神经网络的反向传播，才算入门深度学习！

引言

想象一下，你正在教一个孩子识别猫和狗的照片。刚开始，孩子总是搞错，把猫说成狗，把狗说成猫。但是每次犯错后，你都会告诉他："不对，这是猫！"然后孩子会调整自己的判断标准，下次遇到类似的照片时就能做得更好。

神经网络的学习过程就是这样的！而反向传播（Backpropagation，简称BP）算法就是那个"纠错老师"，它告诉神经网络哪里错了，应该怎么调整。

今天，我们就来亲手计算一遍这个过程，让你真正理解深度学习的核心机制。

什么是反向传播？

生活中的类比

假设你是一家餐厅的老板，想要提高顾客满意度。你的餐厅有三个环节：

采购部门：选择食材质量
厨师团队：烹饪技术
服务团队：服务态度

当顾客给出差评时，你需要找出问题出在哪个环节，然后针对性地改进。这就是反向传播的思想：从结果出发，逐层向前追溯，找出每个环节的责任，然后进行调整。

神经网络中的反向传播

在神经网络中：

前向传播：输入数据从输入层流向输出层，得到预测结果
反向传播：计算预测误差，然后从输出层向输入层传播，更新每层的权重

实战案例：手工计算BP算法

让我们用一个简单的例子来演示整个过程。

场景设定

假设我们要训练一个神经网络来预测房价。输入是房屋面积（单位：100平米），输出是房价（单位：万元）。

我们的网络结构：

输入层：1个神经元（房屋面积）
隐藏层：2个神经元
输出层：1个神经元（房价）

网络结构图

css 复制代码

输入层    隐藏层    输出层
  x  ──→  h1  ──→   y
     ╲  ╱  ╲  ╱
      ╲╱    ╲╱
      ╱╲    ╱╲
     ╱  ╲  ╱  ╲
        h2

初始参数设置

让我们设定初始权重和偏置：

输入层到隐藏层的权重：

w11 = 0.5 （输入到隐藏层第1个神经元）
w12 = 0.3 （输入到隐藏层第2个神经元）

隐藏层到输出层的权重：

w21 = 0.8 （隐藏层第1个神经元到输出）
w22 = 0.6 （隐藏层第2个神经元到输出）

偏置：

b1 = 0.1 （隐藏层第1个神经元）
b2 = 0.2 （隐藏层第2个神经元）
b3 = 0.1 （输出层）

激活函数： 使用Sigmoid函数：σ(x) = 1/(1+e^(-x))

训练数据

输入：x = 1.0 （100平米）
期望输出：t = 0.8 （80万元）

第一步：前向传播

1.1 计算隐藏层输入

ini 复制代码

z1 = w11 × x + b1 = 0.5 × 1.0 + 0.1 = 0.6
z2 = w12 × x + b2 = 0.3 × 1.0 + 0.2 = 0.5

1.2 计算隐藏层输出

scss 复制代码

h1 = σ(z1) = σ(0.6) = 1/(1+e^(-0.6)) ≈ 0.646
h2 = σ(z2) = σ(0.5) = 1/(1+e^(-0.5)) ≈ 0.622

1.3 计算输出层输入

ini 复制代码

z3 = w21 × h1 + w22 × h2 + b3
   = 0.8 × 0.646 + 0.6 × 0.622 + 0.1
   = 0.517 + 0.373 + 0.1
   = 0.990

1.4 计算最终输出

ini 复制代码

y = σ(z3) = σ(0.990) ≈ 0.729

1.5 计算误差

ini 复制代码

E = 1/2 × (t - y)² = 1/2 × (0.8 - 0.729)² ≈ 0.0025

第二步：反向传播

现在开始关键的反向传播过程！

2.1 计算输出层的误差梯度

对于输出层，我们需要计算误差对输出层输入的梯度：

scss 复制代码

δ3 = ∂E/∂z3 = ∂E/∂y × ∂y/∂z3
   = -(t - y) × σ'(z3)
   = -(0.8 - 0.729) × 0.729 × (1 - 0.729)
   = -0.071 × 0.729 × 0.271
   = -0.014

2.2 计算隐藏层的误差梯度

对于隐藏层，误差是从输出层传播回来的：

ini 复制代码

δ1 = ∂E/∂z1 = δ3 × w21 × σ'(z1)
   = -0.014 × 0.8 × 0.646 × (1 - 0.646)
   = -0.014 × 0.8 × 0.646 × 0.354
   = -0.0026

δ2 = ∂E/∂z2 = δ3 × w22 × σ'(z2)
   = -0.014 × 0.6 × 0.622 × (1 - 0.622)
   = -0.014 × 0.6 × 0.622 × 0.378
   = -0.0020

2.3 计算权重梯度

现在我们可以计算每个权重的梯度：

输出层权重梯度：

ini 复制代码

∂E/∂w21 = δ3 × h1 = -0.014 × 0.646 = -0.009
∂E/∂w22 = δ3 × h2 = -0.014 × 0.622 = -0.009

隐藏层权重梯度：

ini 复制代码

∂E/∂w11 = δ1 × x = -0.0026 × 1.0 = -0.0026
∂E/∂w12 = δ2 × x = -0.0020 × 1.0 = -0.0020

偏置梯度：

ini 复制代码

∂E/∂b1 = δ1 = -0.0026
∂E/∂b2 = δ2 = -0.0020
∂E/∂b3 = δ3 = -0.014

第三步：权重更新

使用梯度下降法更新权重，学习率设为 α = 0.5：

ini 复制代码

w21_new = w21 - α × ∂E/∂w21 = 0.8 - 0.5 × (-0.009) = 0.8045
w22_new = w22 - α × ∂E/∂w22 = 0.6 - 0.5 × (-0.009) = 0.6045
w11_new = w11 - α × ∂E/∂w11 = 0.5 - 0.5 × (-0.0026) = 0.5013
w12_new = w12 - α × ∂E/∂w12 = 0.3 - 0.5 × (-0.0020) = 0.3010

b1_new = b1 - α × ∂E/∂b1 = 0.1 - 0.5 × (-0.0026) = 0.1013
b2_new = b2 - α × ∂E/∂b2 = 0.2 - 0.5 × (-0.0020) = 0.2010
b3_new = b3 - α × ∂E/∂b3 = 0.1 - 0.5 × (-0.014) = 0.107

反向传播算法流程图

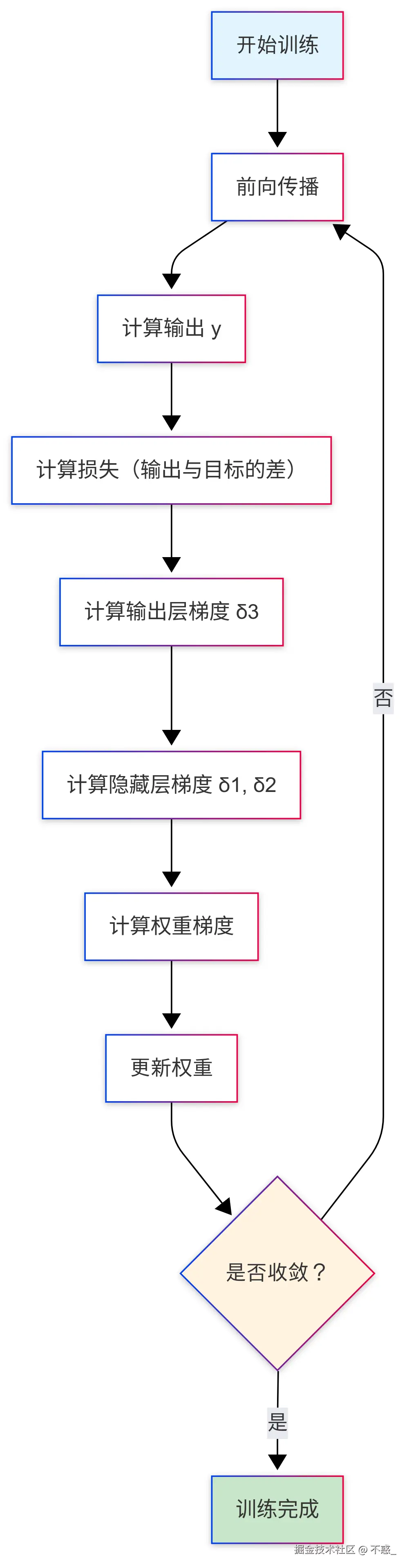
核心公式总结

1. 前向传播

scss 复制代码

z^(l) = W^(l) × a^(l-1) + b^(l)
a^(l) = σ(z^(l))

2. 反向传播

scss 复制代码

δ^(L) = ∇_a C ⊙ σ'(z^(L))           # 输出层误差
δ^(l) = ((W^(l+1))^T δ^(l+1)) ⊙ σ'(z^(l))  # 隐藏层误差

3. 梯度计算

scss 复制代码

∂C/∂w^(l) = a^(l-1) δ^(l)
∂C/∂b^(l) = δ^(l)

4. 权重更新

scss 复制代码

w^(l) = w^(l) - α × ∂C/∂w^(l)
b^(l) = b^(l) - α × ∂C/∂b^(l)

为什么反向传播如此重要？

1. 效率优势

如果我们要计算一个有1000万个参数的网络的梯度，直接计算需要进行1000万次前向传播。而反向传播只需要一次前向传播和一次反向传播，效率提升了几个数量级！

2. 数学优雅性

反向传播利用了链式法则，将复杂的梯度计算分解为简单的局部计算，每一层只需要关心自己的输入和输出。

3. 通用性

无论网络有多深、多复杂，反向传播算法都能适用，这为深度学习的发展奠定了基础。

实际应用中的注意事项

1. 梯度消失问题

在很深的网络中，梯度可能会变得非常小，导致前面的层几乎不更新。解决方案包括：

使用ReLU等激活函数
批量归一化
残差连接

2. 梯度爆炸问题

梯度可能会变得非常大，导致权重更新过度。解决方案：

梯度裁剪
合适的学习率
权重初始化

3. 学习率选择

太大：可能错过最优解
太小：收敛速度慢
解决方案：自适应学习率算法（Adam、RMSprop等）

代码实现示例

python 复制代码

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

class SimpleNeuralNetwork:
    def __init__(self):
        # 初始化权重
        self.w1 = np.array([[0.5], [0.3]])  # 输入到隐藏层
        self.w2 = np.array([[0.8, 0.6]])    # 隐藏层到输出
        self.b1 = np.array([[0.1], [0.2]])  # 隐藏层偏置
        self.b2 = np.array([[0.1]])         # 输出层偏置
    
    def forward(self, x):
        # 前向传播
        self.z1 = np.dot(self.w1, x) + self.b1
        self.a1 = sigmoid(self.z1)
        self.z2 = np.dot(self.w2, self.a1) + self.b2
        self.a2 = sigmoid(self.z2)
        return self.a2
    
    def backward(self, x, y, output):
        # 反向传播
        m = x.shape[1]
        
        # 计算输出层梯度
        dz2 = output - y
        dw2 = (1/m) * np.dot(dz2, self.a1.T)
        db2 = (1/m) * np.sum(dz2, axis=1, keepdims=True)
        
        # 计算隐藏层梯度
        dz1 = np.dot(self.w2.T, dz2) * sigmoid_derivative(self.a1)
        dw1 = (1/m) * np.dot(dz1, x.T)
        db1 = (1/m) * np.sum(dz1, axis=1, keepdims=True)
        
        return dw1, db1, dw2, db2
    
    def update_parameters(self, dw1, db1, dw2, db2, learning_rate):
        # 更新权重
        self.w1 -= learning_rate * dw1
        self.b1 -= learning_rate * db1
        self.w2 -= learning_rate * dw2
        self.b2 -= learning_rate * db2

# 使用示例
nn = SimpleNeuralNetwork()
x = np.array([[1.0]])  # 输入
y = np.array([[0.8]])  # 期望输出

for i in range(1000):
    # 前向传播
    output = nn.forward(x)
    
    # 反向传播
    dw1, db1, dw2, db2 = nn.backward(x, y, output)
    
    # 更新参数
    nn.update_parameters(dw1, db1, dw2, db2, 0.5)
    
    if i % 100 == 0:
        loss = 0.5 * (y - output) ** 2
        print(f"Epoch {i}, Loss: {loss[0][0]:.6f}")

总结

反向传播算法是深度学习的核心，它让我们能够训练复杂的神经网络。通过这次手工计算，我们理解了：

前向传播：数据如何在网络中流动
损失计算：如何衡量预测的好坏
反向传播：如何计算每个参数的梯度
参数更新：如何根据梯度调整权重

记住，理解算法的数学原理是成为深度学习专家的必经之路。只有真正理解了反向传播，你才能：

调试网络训练中的问题
设计更好的网络架构
优化训练过程
创新新的算法

现在，你已经真正入门深度学习了！下一步，可以尝试实现更复杂的网络，或者深入学习各种优化算法。记住，实践是最好的老师，多动手编程，多做实验，你会发现深度学习的无穷魅力！