在笔记:卷积神经网络(CNN)-CSDN博客中,我们在8.1.中引入了有局部感受野这一概念,是指在全连接层中神经元在灰度图中所对应的大小,也就是该神经元负责接收这个范围内数据与卷积核计算出来的特征图中的数据。
另外我们还提到,卷积核(过滤器)的个数是超参数,是人为确定下来的,卷积核的个数意味着需要使用神经元的个数,卷积核的优化需要基于全连接层的反馈。
因此我们不由得思考:
在深层卷积网络中,卷积核是可以有多层的,多层卷积核对后续的计算会有什么影响?
这里就引入了我们本次文的重点:有效感受野。
我们进行一个简单的推导:
一个8*8的图像,设卷积核尺寸为3*3,步长为1,有三层过滤器,计算最后面一层的感受野是多少。
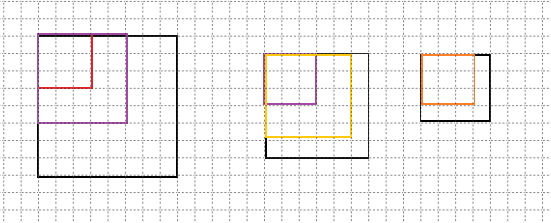
如图所示,最左侧的8*8为灰度图,
第一个图中的红色框描述的是第一轮卷积核在扫描时覆盖的范围,
第二个图中的紫色框描述的是第二轮卷积核在扫描时覆盖的范围,
第三个图中的橙色框描述的是第三轮卷积核在扫描时覆盖的范围。
显而易见的是:
第一个图中的紫色框经过扫描后恰恰生成的是第二个图(第一轮生成特征图)中的紫色框部分。
第二个图中的橙色框经过扫描后恰恰生成的是第二个图(第二轮生成特征图)中的橙色框部分。
而第三个图中橙色框如果进行扫描的话仅仅只生成一个格子(第三轮生成特征图,没画出来)。
因此我们可以反向推导一波:
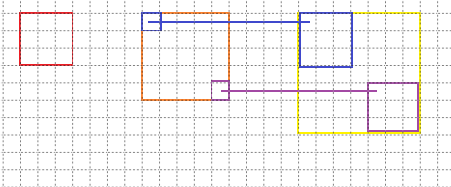
显而易见,黄框中左上角的3*3蓝框,在扫描过后位于特征图的位置和蓝框内左上角的元素一样都为(1,1),同理,紫框扫描后的位置是(5,5)。
我们发现:每经过一次扫描,特征图大小就缩小了k-1,k为卷积核边长。
那我们得出了m=n-k+1 m为特征图的尺寸,n为灰度图(或者是输入特征图)的尺寸。
准确来说这是当图片为正方形且步长为1时的计算公式。
保持原条件反推,那么k*k的过滤器,在n轮过滤后的有效视野为 y=k+n*(k-1)=(k-1)*(n+1) + 1
因此,在3*3过滤,且过滤三层的情况下,一个神经元的有效感受野是7*7
如果步长不为1怎么办?
我们引入通用公式:
