
写在最前
LoRA 全称为 Low-Rank Adaptation,翻译成中文就是低秩适配
⊙﹏⊙ 是不是一头雾水?没关系,相信我,看完下文你就会明白个大概了
那如果还不懂怎么办呢?那就请狠狠的给我一键三连,以示鼓励吧 ¬‿¬
直入正文
丹尼尔:蛋兄,我常常听到 LoRA 微调,那什么是 LoRA 呢?它又为什么可以加速微调呢?原理是什么呢?
蛋先生:这个问题问得好!但是能不能别一下子全问完,不然这篇文章就没法写了 ╮(╯▽╰)╭
丹尼尔:😜 Sorry!那先说说什么是 LoRA 吧
蛋先生:LoRA 全称 Low-Rank Adaptation,中文叫低秩适配。
丹尼尔:开头讲过啦,看名字看不出什么啊,是不是名字起得不好,不能顾名思义?(¬_¬)
蛋先生:别急,等会我讲完原理,你就会觉得这个名字其实起得挺好的 ( ̄▽ ̄)ノ
先说说 LoRA 是什么吧,它是一种非常流行的大模型微调方法。大模型的参数很多,每个参数都去调整的话不仅消耗资源,而且并不是每个参数的调整都有意义。因此,我们需要一种方法,通过调整少量参数就能让大模型适应特定领域的任务,这就是 LoRA 的由来。
简单来说,LoRA 就是只调整模型权重里很小一部分参数,让预训练模型更好地适应特定(通常是小规模)的数据集 (๑•̀ㅂ•́)و✧
丹尼尔:它是怎么做到只调整一小部分参数的呢?
蛋先生:假设预训练大模型的原始权重参数为 W⁰,经过微调后的权重参数为 W,那么就有以下公式
ini
W = W⁰ + △W丹尼尔:这个 △W 就是权重参数调整的量(权重更新矩阵),也就是我们要学习的部分是吗?
蛋先生:没错!假设 W⁰ 是 100×100 的矩阵,那么 △W 也是 100×100 的矩阵,请问总共需要调整多少个参数?
丹尼尔:1 万啊
蛋先生:真聪明 ( ̄▽ ̄)b
丹尼尔:我谢谢你的夸奖哦,把我当小学生了 (╯°□°)╯
蛋先生:1 万个参数都调,这种称为全量微调
丹尼尔:那 LoRA 怎么优化?(o゚▽゚)o
蛋先生:别急,我们再来看一个矩阵乘积 AB(A 矩阵乘以 B 矩阵),A 是 100×{rank} 的矩阵,B 是 {rank}×100 的矩阵,它们的结果是什么形状的矩阵呢?
丹尼尔:无论 rank 取多少,AB 的结果都正好是 100×100 的矩阵。咦,这个结果正好跟 △W 形状一样!(⊙o⊙)
蛋先生:对了!所以在 LoRA 中,我们不再学习一个完整的 △W,而是直接把它参数化为 AB,这样天然就是低秩的。如果 rank 取 10,那么这两个矩阵共有多少个值(权重参数)呢?
丹尼尔:让我算算...100×10 + 10×100 = 2000 个参数!(≧∇≦)ノ
蛋先生:聪明!原来是 10000 个参数,现在只要 2000 个,只有原来的五分之一
丹尼尔:但有个疑问,△W≈A@B 这个为什么成立呢?
蛋先生:语言模型在下游任务中,不需要"彻底改写"原有能力,而是"往某些方向上调整"。这些调整在数学上往往集中在低秩子空间,所以这样做不会损失太多效果。就像画画时,你只需要在关键位置勾几笔,而不是把整张画重画一遍。
丹尼尔:如果 rank 取更少,那岂不是参数更少了
蛋先生:回到 LoRA 名称中的 low rank,不就是指这里要取更少的维度吗
丹尼尔:原来如此。那具体怎么应用到模型中?
蛋先生:我们可以选择原来的部分全连接层替换为 LoRA 层,用公式表示就是将 XW 替换成 XW⁰+XAB。
ini
XW = X(W⁰+AB) = XW⁰+XAB丹尼尔:哇,我好像看出来了,这里就体现了 adaption 适配!
蛋先生:没错!因为它不修改原来的权重,只是加了个扩展。编程原则有个开闭原则,对修改关闭,对扩展开放,这里就是这样的。
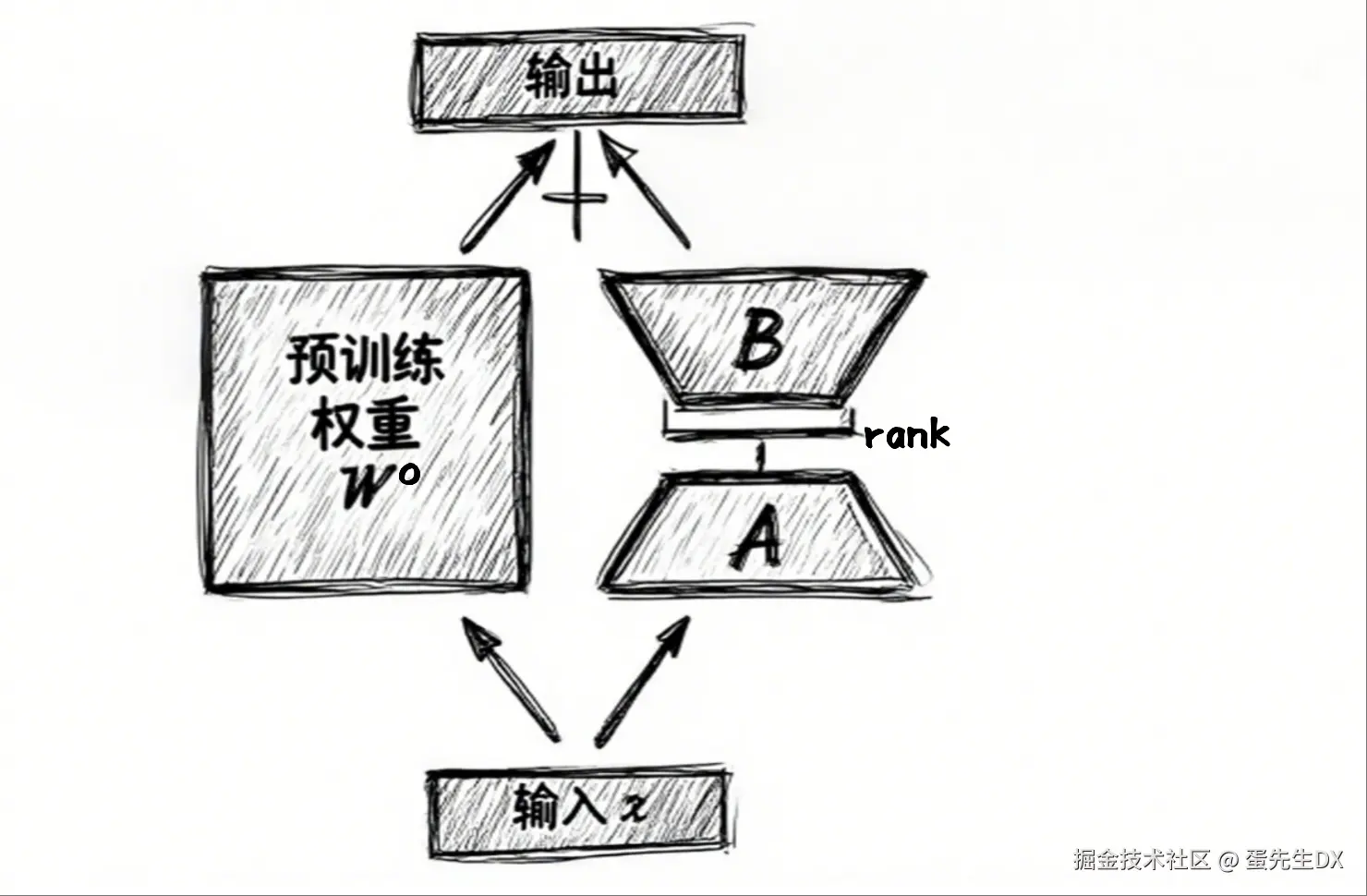
丹尼尔:那 W⁰ 和 A、B 怎么训练?
蛋先生:其中 W⁰ 是冻结的,我们只微调 A 和 B 即可。
丹尼尔:计算效率怎么样?
蛋先生:在训练时,前向传播虽然多了一次矩阵乘法,但因为参数大幅减少,反向传播的开销也随之下降,所以整体微调速度反而更快。而在推理时,可以把 W⁰+AB 合并成一个整体,几乎不会增加额外计算量。
丹尼尔:原来如此!那除了 A 和 B,还有别的可调参数吗?
蛋先生:当然,LoRA 公式中还会有缩放因子,rank 和缩放因子都属于超参数,可以在训练过程中进行调整。
丹尼尔:现在来看,LoRA 的名字起得确实不错
写在最后
在此声明,以上内容并不严谨。严谨与通俗易懂在表达上往往难以兼顾,就像安全与便利常常难以平衡一样 ( ̄~ ̄; )
因此,建议有兴趣的同学,在此基础上,自行查阅专业资料以获得更深入的了解
亲们,都到这了,要不,点赞或收藏或关注支持下我呗 o( ̄ ▽  ̄)d