一 概念
1 决策节点
通过条件判断而进行分支选择的节点。
将样本的属性值,也就是特征值与决策节点上的值进行比较,从而判断它的流向。
2 叶子节点
没有子节点的节点,表示最终的决策结果。
3 决策树的深度
所有节点的最大层次数
决策树具有一定的层次结构,根节点的层次数定为0,从下面开始每一层子节点层次数增加。
4 决策树优缺点
优点:可视化、可解释能力、对算力要求低;
缺点:容易产生过拟合,所以不要把深度调整太大;
二 基于信息增益决策树的建立
信息增益决策树倾向于++选择取值较多的属性++。
有些情况下,这类属性可能不会提供太多有价值的信息,算法只能对描述属性为离散型属性的数据集构造决策树。
1 信息熵
信息熵描述的是不确定性。
信息熵越大,不确定性越大。信息熵的值越小,则样本集合D的纯度越高。
假设样本集合D共有N类,第K类样本所占比例为pk,则样本集合D的信息熵为:
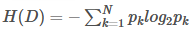
2 信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力。
信息增益越大,那么决策树就会越简洁。
信息增益的程度用信息上的变化程度来衡量:IG(Y|X)=H(Y)-H(Y|X)≥0
3 信息增益决策树建立步骤
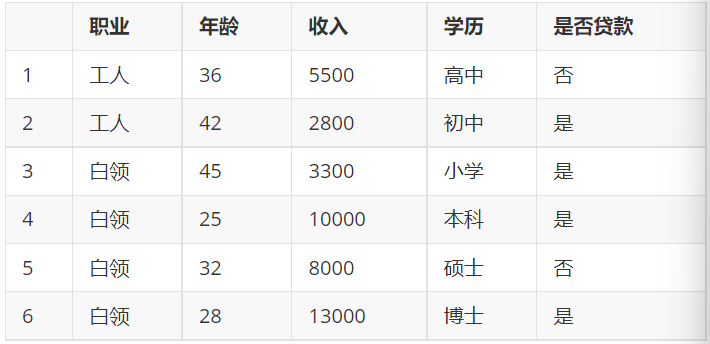
3.1 计算根节点的信息熵
上表把是否贷款分为2类样本:"是"占2/3,"否"占1/3;
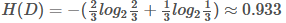
3.2 计算属性的信息增益
3.2.1职业 属性的信息增益
IG(D,"职业")
在职业中,工人占1/3,工人中,是否贷款各占1/2,所以: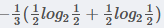
在职业中,白领占2/3, 白领中,是贷款占3/4, 不贷款占1/4, 所以有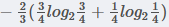
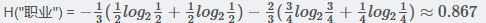

3.2.2 年龄 属性的信息增益
(以35岁为界)

3.2.3 收入 属性的信息增益
(以10000为界,大于等于10000为一类)
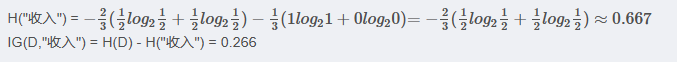
3.2.4 学历 属性的信息增益
(以高中为界, 大于等于高中的为一类)
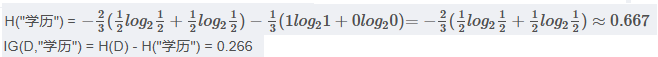
注意:
以上年龄使用35为界,收入使用10000为界,学历使用高中为界。
实计API使用中,会有一个参数"深度", 属性中具体以多少为界会被根据深度调整。
3.3 划分属性
对比属性信息增益发现,"收入"和"学历"相等,并且是最高的,所以我们就可以选择"学历"或"收入"作为第一个决策树的节点, 接下来我们继续重复3.1、3.2的做法继续寻找合适的属性节点。
三 基于基尼指数决策树的建立
基尼指数是指决策树算法中用于评估数据集纯度的一种度量,衡量的是数据集的不纯度,也可以说是分类的不确定性。
在构建决策树时,基尼指数被用来决定如何对数据集进行最优划分,以减少不纯度。
对于一个二分类问题,如果一个节点包含的样本属于正类的概率是 (p),则属于负类的概率是 (1-p)。
这个节点的基尼指数 (Gini(p)) 定义: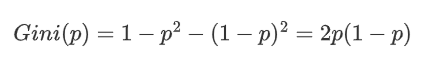
对于多分类问题,如果一个节点包含的样本属于第 k 类的概率是 p_k,则节点的基尼指数定义为:
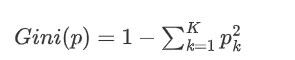
3.1 基尼指数的意义
1、当一个节点的所有样本都属于同一类别,基尼指数为0,表示纯度最高。
2、当一个节点的样本均匀分布在所有类别时,基尼指数最大,表示纯度最低。
3.2 决策树中的应用
构建决策树的时候,希望每个内部节点的子节点能更纯,也就是基尼指数更小。
那么选择分割特征和分割点的目标是使子节点的平均基尼指数最小化。具体就是对一个特征,我们计算其所有的可能的分割点对应的子节点的加权平均基尼,选择最小化这个值的分割点。这个过程会在所有特征中重复,知道找到最佳的分割特征和分割点。
考虑一个数据集D,其中包含N个样本,特征A将数据集分割为|D1|和|D2|,则特征A的基尼指数为:,其中|D1|和|D2|分别是子集D1和D2的样本数量。
通过这样的方式,决策树算法逐步构建一棵树,每层的节点都尽可能减少基尼指数,最终达到对数据集的有效分类。
四 API
class sklearn.tree.DecisionTreeClassifier(....)参数:
criterion "gini" "entropy" 默认为="gini"
当criterion取值为"gini"时采用 基尼不纯度(Gini impurity)算法构造决策树,
当criterion取值为"entropy"时采用信息增益( information gain)算法构造决策树.
max_depth int, 默认为=None 树的最大深度
可视化决策树
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)参数:
estimator决策树预估器
out_file生成的文档
feature_names节点特征属性名
功能:
把生成的文档打开,复制出内容粘贴到"http://webgraphviz.com/"中,点击"generate Graph"会生成一个树型的决策树图