【LeetCode热题100道笔记】腐烂的橘子

题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；

值 1 代表新鲜橘子；

值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

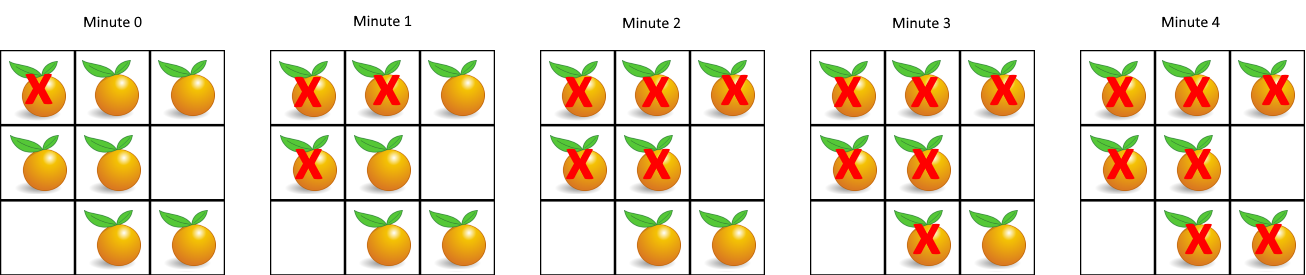
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]

输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]

输出：-1

解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]

输出：0

解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length

n == grid[i].length

1 <= m, n <= 10

grid[i][j] 仅为 0、1 或 2

思考一：暴力模拟（基于分钟迭代的广度扩散）

该算法通过逐分钟模拟腐烂橘子的扩散过程来解决问题，核心思路是：

1. 记录初始状态下所有新鲜橘子的数量
2. 每过一分钟，让当前所有腐烂的橘子同时向四周扩散，感染相邻的新鲜橘子
3. 重复扩散过程，直到没有新鲜橘子或无法继续扩散为止
4. 若最终仍有新鲜橘子未被感染，则返回-1

算法过程：

1. 初始化准备：

   • 统计初始新鲜橘子的数量count
   • 创建visited二维数组，用于标记橘子的状态（0=未处理，1=本轮刚腐烂，2=已完成扩散）
   • 定义四个方向的偏移量directions（上下左右）

2. 循环模拟扩散过程：

   • 当仍有新鲜橘子（count > 0）时，进入下一分钟的扩散
   • 重置visited数组中"本轮刚腐烂"的标记（将1重置为0）
   • 遍历整个网格，对每个已腐烂且未完成扩散的橘子（grid[i][j] === 2 && !visited[i][j]）：
     • 检查其四个方向的相邻单元格
     • 若相邻单元格是新鲜橘子（grid[x][y] === 1），则将其标记为腐烂，同时更新count和visited
     • 标记当前腐烂橘子已完成扩散（visited[i][j] = 2）
   • 若本轮没有任何橘子被腐烂（flag仍为false），说明无法继续扩散，返回-1
   • 否则，分钟数ans加1

3. 终止条件：

   • 当所有新鲜橘子都被腐烂（count === 0），返回所用分钟数ans
   • 若中途发现无法继续扩散且仍有新鲜橘子，返回-1

算法特点：

• 优点：直观模拟了橘子腐烂的过程，逻辑易于理解
• 缺点：需要多次遍历整个网格，时间复杂度较高（O(kmn)，其中k为最大分钟数）
• 核心技巧：使用visited数组避免同一分钟内的重复感染（确保每个新鲜橘子只在被首次感染时计数）

该算法通过逐分钟迭代的方式，确保了同一时间点所有腐烂橘子的扩散是同步进行的，符合题目中"每分钟腐烂橘子周围的新鲜橘子同时腐烂"的要求。

代码

/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function(grid) {
    const [m, n] = [grid.length, grid[0].length];
    const visited = Array.from({ length: m }, () => Array(n).fill(0));
    const directions = [[-1, 0],[1, 0], [0, -1], [0, 1]];


    let ans = 0, count = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === 1) {
                count++;
            }
        }
     } 
    

    while (count > 0) {
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (visited[i][j] === 1) {
                    visited[i][j] = 0;
                }
            }
        }
        let flag = false;
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (grid[i][j] === 2 && !visited[i][j]) {
                    for (let [a, b] of directions) {
                        if (i + a < 0 || i + a >= m || j + b < 0 || j + b >= n) continue;
                        if (grid[i+a][j+b] === 1 && !visited[i+a][j+b]) {
                            grid[i+a][j+b] = 2;
                            visited[i+a][j+b] = 1; // 本轮已访问
                            count--;
                            flag = true;
                        }
                    }
                    visited[i][j] = 2;
                }
            }
        }
        if (!flag) return -1;
        flag = false;
        ans++;
    }
    
    return ans;
};

思考二：多源广度优先搜索（Multi-source BFS）

该算法针对"多个腐烂橘子同时扩散"的场景优化，核心思想是：

将所有初始腐烂的橘子视为"同一层级的起点"，通过 BFS 同时向四周扩散，每扩散一层代表经过 1 分钟。利用 BFS 层级遍历的特性，确保记录的扩散时间是"最短时间"，同时避免重复处理，最终高效判断是否所有新鲜橘子都能被腐烂。

算法过程（分 4 步）

步骤 1：初始化 - 收集起点与统计状态

1. 参数准备 ：
   • 获取网格的行数 M 和列数 N，定义四个方向的偏移量 directions（上下左右）。
   • 初始化队列 queue（存储待扩散的腐烂橘子）、哈希表 depth（记录每个橘子被腐烂的时间）、计数器 count（统计初始新鲜橘子数量）。
2. 遍历网格初始化 ：
   • 若单元格为新鲜橘子（grid[i][j] === 1），count 加 1；
   • 若单元格为腐烂橘子（grid[i][j] === 2）：
     • 将橘子位置编码为唯一值 code = i * N + j（避免存储二维坐标，简化操作），加入队列 queue；
     • 在 depth 中记录该橘子的腐烂时间为 0（初始时刻）。

步骤 2：多源 BFS 扩散 - 同步模拟腐烂过程

1. 循环处理队列 ：
   当队列不为空时，依次取出队首的腐烂橘子（按层级顺序，确保同一分钟的腐烂橘子同步处理）：
   • 解码位置：通过 code 反推橘子的坐标 i = Math.floor(code / N)、j = code % N；
   • 四向扩散：对每个方向的相邻单元格 (ni, nj) 进行合法性检查：
     • 坐标合法：ni 在 [0, M) 且 nj 在 [0, N)；
     • 状态合法：相邻单元格为新鲜橘子（grid[ni][nj] === 1）。
   • 处理新鲜橘子：
     • 将其标记为腐烂（grid[ni][nj] = 2）；
     • 编码新腐烂橘子的位置，加入队列（用于下一层扩散）；
     • 记录其腐烂时间为"当前橘子时间 + 1"（depth.set(ncode, depth.get(code) + 1)），并更新最大时间 ans；
     • 新鲜橘子数量 count 减 1。

步骤 3：判断终止条件 - 新鲜橘子是否残留

1. 当队列遍历结束后，检查 count 的值：
   • 若 count === 0：所有新鲜橘子已被腐烂，返回最大时间 ans；
   • 若 count > 0：存在无法腐烂的新鲜橘子（如被空单元格隔离），返回 -1。

步骤 4：特殊场景处理

• 若初始无新鲜橘子（count 初始为 0）：队列遍历不执行，直接返回 ans = 0（符合"0 分钟无新鲜橘子"的场景）；
• 若初始只有腐烂橘子/空单元格：同样返回 0。

算法核心优势

1. 同步扩散：多个初始腐烂橘子同时作为起点，避免"逐个 BFS 再合并结果"的冗余计算，时间复杂度优化至 O(M*N)（仅遍历网格 2 次：初始化 + BFS）；
2. 时间准确性 ：BFS 层级遍历确保每个橘子被腐烂的时间是"最短时间"，ans 记录的是全局最晚腐烂的时间（即总耗时）；
3. 状态清晰 ：通过 grid 标记橘子状态、depth 记录时间，无需额外二维数组，空间利用率更高。

代码

/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function(grid) {
    const [M, N] = [grid.length, grid[0].length];
    const directions = [[-1, 0],[1, 0], [0, -1], [0, 1]];

    let ans = 0, count = 0, queue = [], depth = new Map();
    for (let i = 0; i < M; i++) {
        for (let j = 0; j < N; j++) {
            if (grid[i][j] === 1) {
                count++;
            } else if (grid[i][j] === 2) {
                const code = i * N + j;
                queue.push(code);
                depth.set(code, 0); // 橘子位置编码：橘子被腐烂的时间
            }
        }
    } 
    
    while (queue.length) {
        const code = queue.shift();
        let i = Math.floor(code / N), j = code % N;
        for (let [dx, dy] of directions) {
            let ni = i + dx, nj = j + dy;
            if (ni < 0 || ni >= M || nj < 0 || nj >= N || grid[ni][nj] !== 1) continue;
            grid[ni][nj] = 2;
            const ncode = ni * N + nj;
            queue.push(ncode);
            depth.set(ncode, depth.get(code) + 1)
            ans = depth.get(ncode);
            count--;
        }
    }
    
    return count !== 0 ? -1 : ans;
};