离散数学
- 前言
- [第一章 命题逻辑](#第一章 命题逻辑)
- [第二章 谓词逻辑](#第二章 谓词逻辑)
前言
- 首先说一下我对于这门课的学习方法 这门学科和概率论真的强相关 其中很多符号和性质都非常相似 还有一部分是和线代以及数据结构相关 建议对比起来学习 会轻松很多 而不是完全当成一个全新的学科来做
- 学习建议:我认为把 前面两章学好是非常重要的 知识点高度集中 能否快速适应灵活变通我觉得是重中之重
随着学习愈发的深入 大家会渐渐明白 明明是叫离散数学 但这门课为什么会是计算机大类的核心课程 我觉得把这门课学好对于数理逻辑的提升是很大的 并且这是计算机相关设计的基础 这是能够实实在在帮助我们解决实际问题的 例如: 当给你一个比较复杂的开关/逻辑电路 如何进行化简的问题- 在此特别感谢电子科技大学团队的学习资源分享 对应课程链接
我往往对于线上的课程是很挑剔的 在我尝试很多课程之后 才找到了最适合我的 虽然不是最新版 但是并不影响观看学习 真还得是国家精品课程 课程评论区置顶 这就是我的心声课程评价:

第一章 命题逻辑
命题与命题联结词
合取与析取联结词
- 其实这些所谓的连接词跟概率论密不可分 并不是什么新鲜的概念
- 比如合取就是交------>并且 析取就是并------>或者可以这么来说:
- 析取就是取并集 合取就是取交集 长的形状只不过是将U改成了V

- 合取
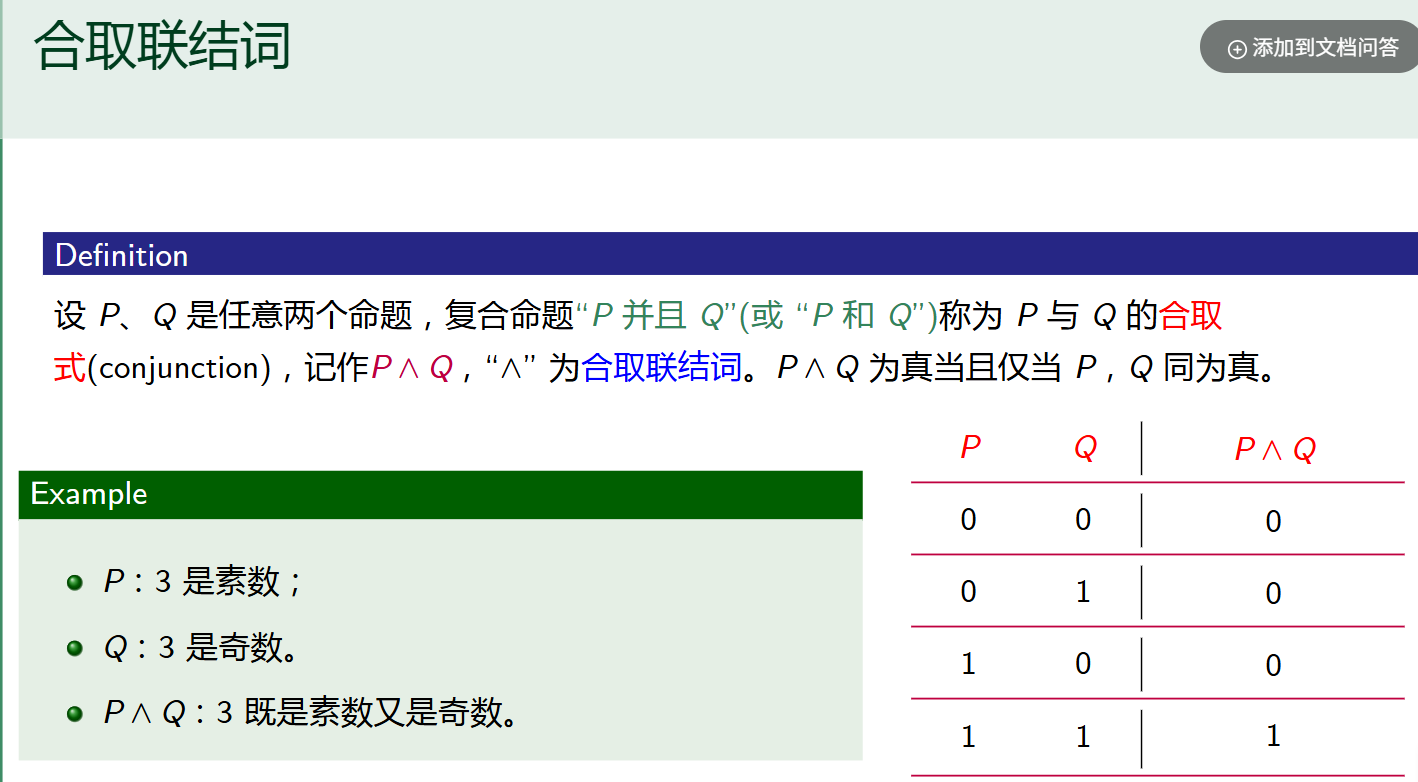
- 析取
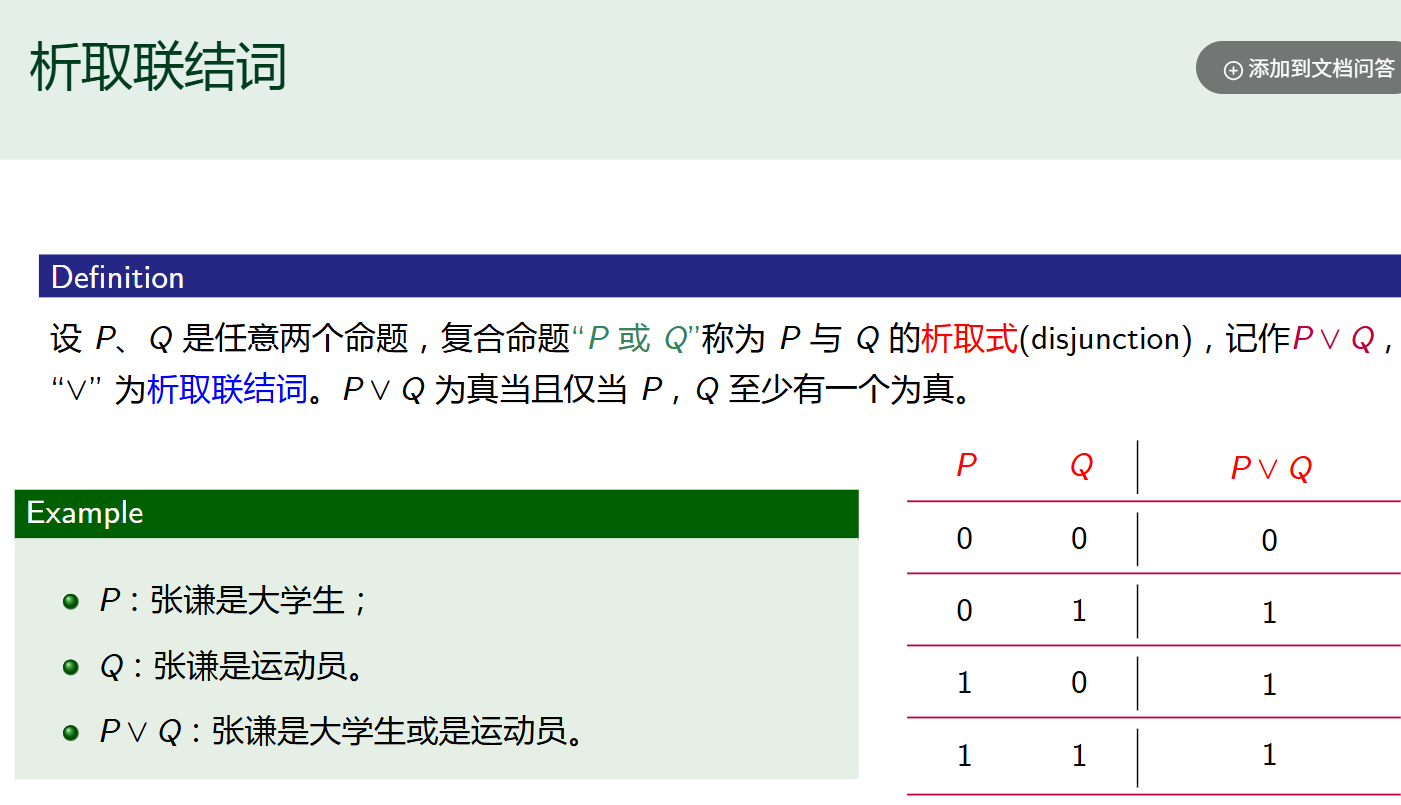
蕴含链接词
- 这个东西和我们平时的概率论中的与或非不同 更多的是像数学当中的命题或者是逆否命题
- 对于两个命题用某个连接词的链接起来的不同情况会列成一个表格 就叫做真值表
- 关键是只有P真Q假的时候 才算假 0
- 下面可以用一个常见的例子帮助我们理解

等价链接词
- 如何理解等价链接词以及区分于蕴含链接词:
- "同真同假则为真,一真一假则为假"。它和蕴含联结词的区别在于:蕴含是单向约束,等价是双向绑定。

命题公式(真值函数)&真值表
-
毕竟是数学 我们可以将这个真值函数 类比于高数中的二元函数来理解 当x y确定之后函数值也随之确定了
-
类比到这里 我们就可以将每一个命题变量 看做为一个未知数 我们对于命题变量取不同的值 结果导致真值函数G的值随之发生变化

-
这是在熟练上面几个联结词之后的基础上来写的
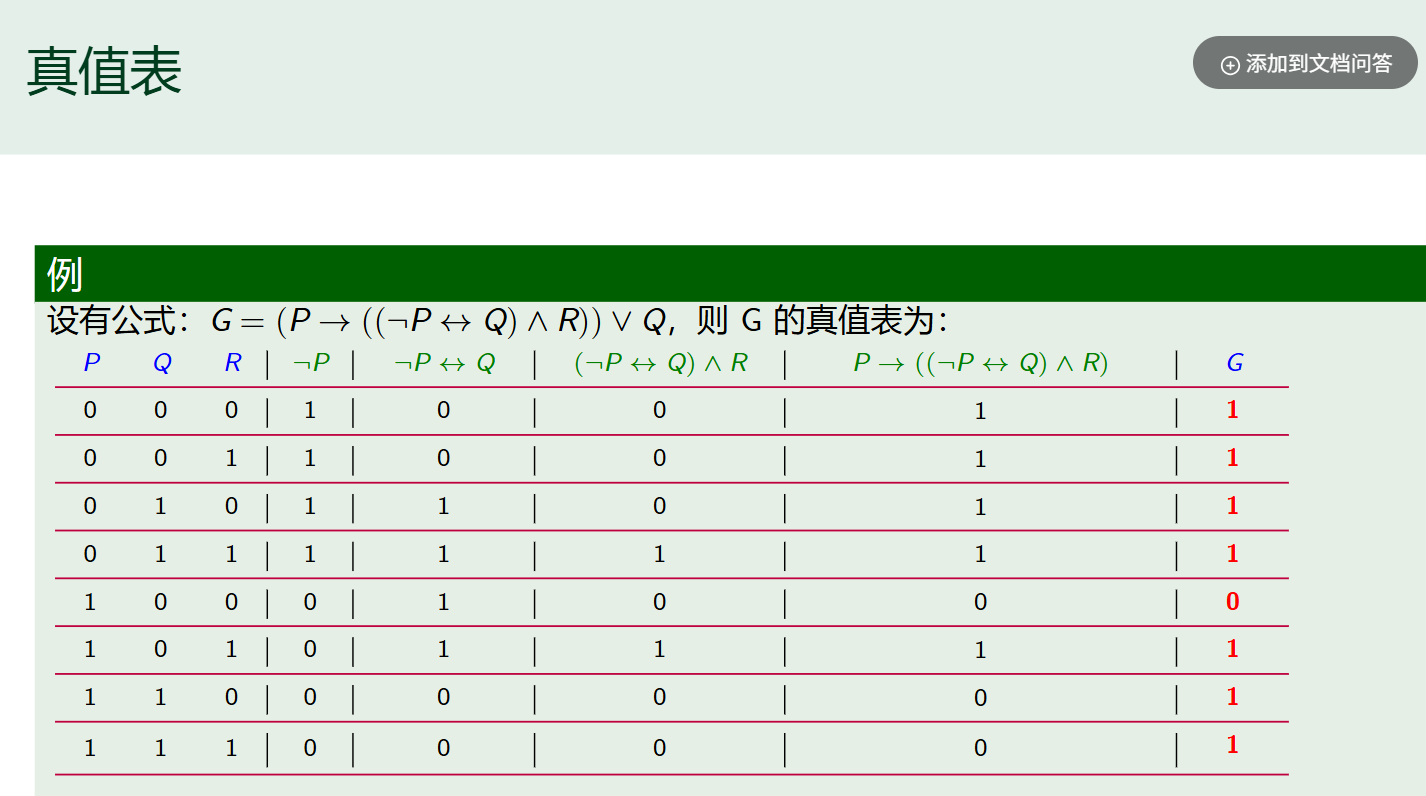
命题公式的分类及等价

真值表联系
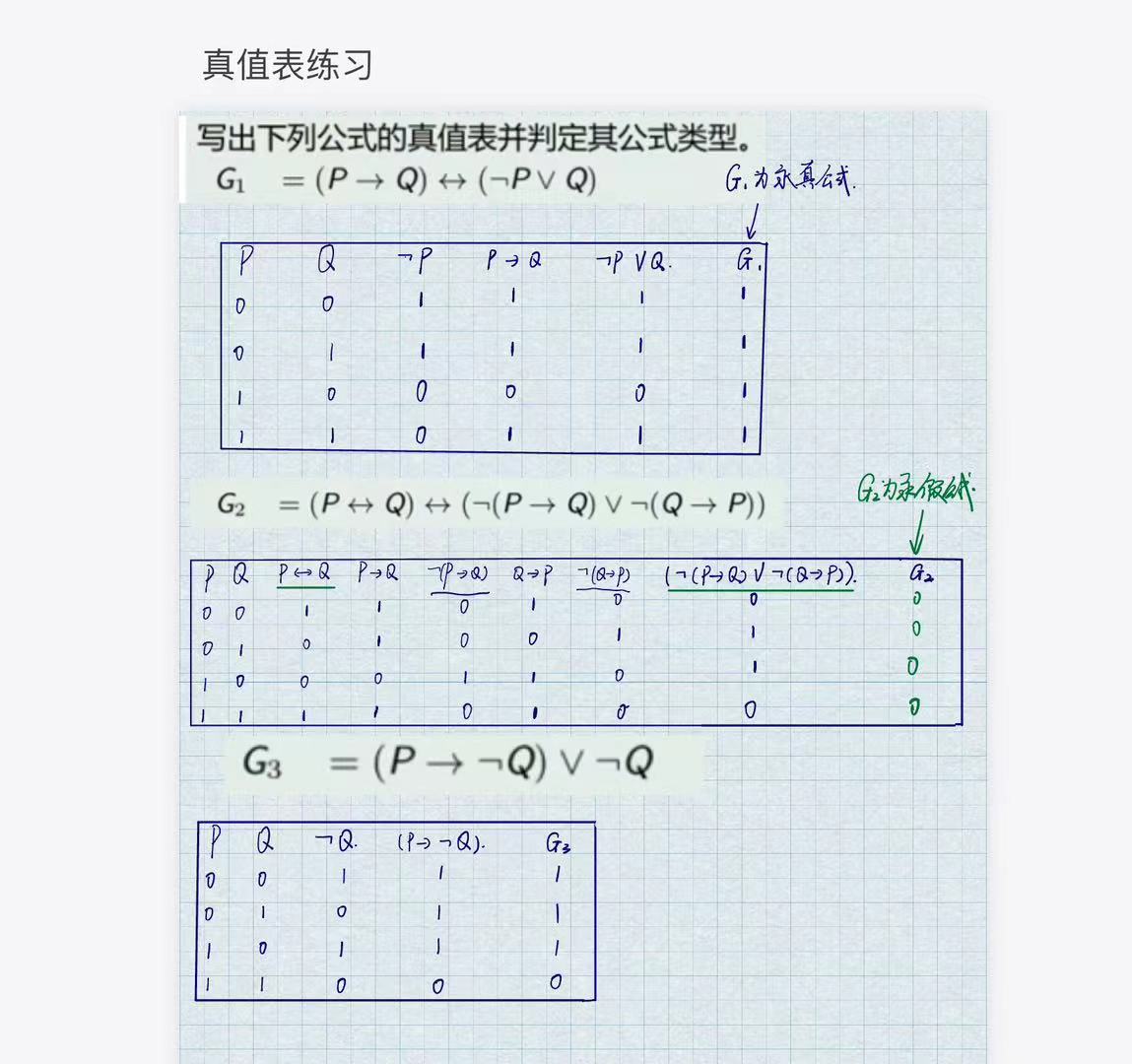
命题的等价公式及应用(重要)
判断公式类型

证明公式等价

开关电路化简
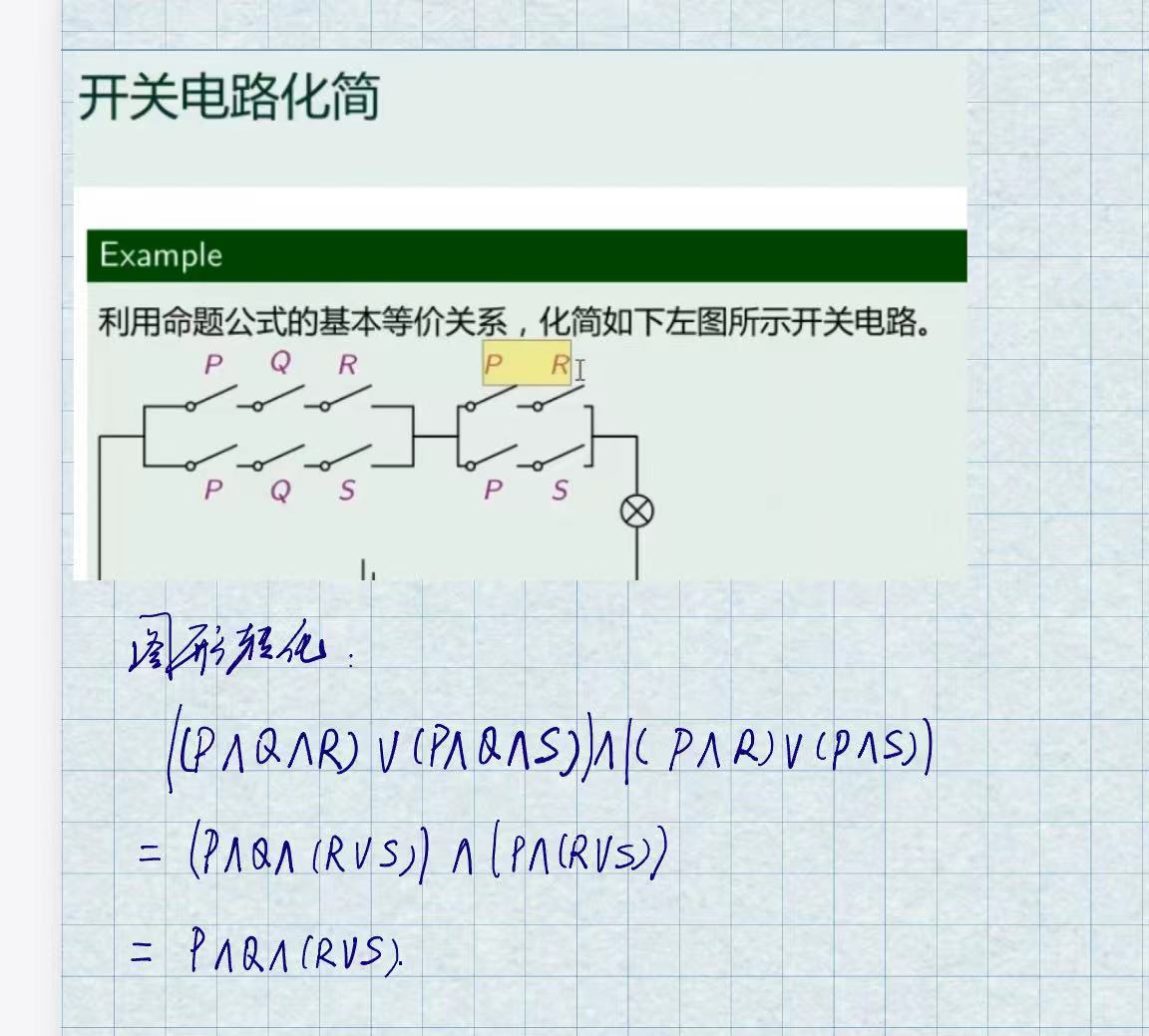
范式
- 有了前面真值表的学习 我们会发现 如果有三个命题变元 那么对应真值表就有8行 因为2的三次方是8 可以看成是二进制的表示来理解 但如果这个时候有100个命题变元 那么画出这个真值表就变成了痛苦的代名词

析取范式 & 合取范式

范式的存在和求解定理
- 由于对于任意的命题公式都存在与其等价的析取范式以及合取范式 那么我们

- 由于析取以及合取范式里面是不存在蕴含以及等价联结词的 所以我们就需要通过前面的公式进行转化 这是非常关键的

- 这里析取和合取写反了QWQ

范式与真值
- 其实通过上面的学习 我们还是没有真正领悟范式的精髓作用所在 它之所以能够替代真值表 那么它一定能够指出公式何时为真或为假
- 我们可以以下面这个蓝色的例子来看 :
- 他有三个命题变元 P Q R 并且这明显是一个合取范式 那么它所连接的左右两个部分只要有一个为假 结果为假
- 假设左边为假 而左边是 (非P V Q)只要非P或者Q为假的时候整体就为假 这时候和R的取值就无关了
- 如果假设右边为假 而右边是( P V 非R ) 只要P或者非R有一个为假那么整体为假 这时候和Q就无关了
- 经过分析 我们发现合取范式确确实实可以指出公式何时为假 从而能够替代真值表 析取范式也是同理

主范式(重要)
引入
- 为什么一般来说,若有n个命题变元,则应有2^n 个不同的极小项和2的n次方 个不同的极大项。
- 一方面是由于前面我们所说的命题变元对于结果的影响是2的n次方的 另一方面我们极小项以及极大项最重要的区别是 极小项是合取 极大项是析取

极小项的性质
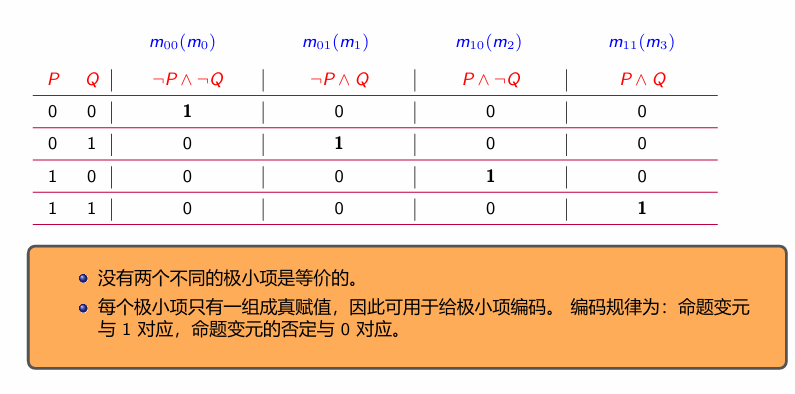
极大项的性质
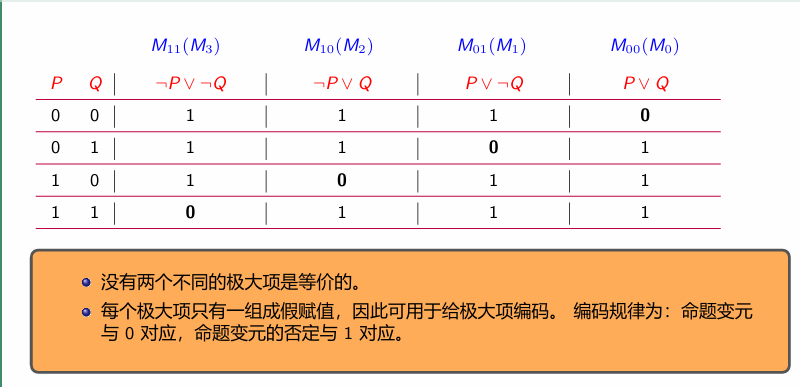
极小项和极大项编码
- 这里的编码是非常容易混淆的 如果是给出了极大/小项 那么我们只需要直接写出其对应编码就好了
- 给定编码(十进制)一般的步骤:
- 先将其二进制写出来 然后确定到底是极小项还是极大项 然后写出对应极小项或极大项

主析取范式 & 主合取范式

范式求解方法
公式转换法
真值表法
经典习题分析
第二章 谓词逻辑
结语
