数据结构之链表（单向链表与双向链表）

hsjkdhs2025-09-09 12:11

一，链表描述

链表是一种常见的重要的数据结构,是动态地进行存储分配的一种结构。常用于需存储的数据的数目无法事先确定。

1.链表的一般结构

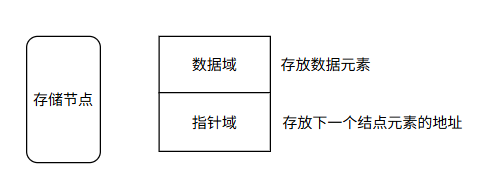
链表的组成：

头指针：存放一个地址，该地址指向一个元素

结点：用户需要的实际数据和链接节点的指针

2.结点结构体类型的定义

链表结点结构的 一般形式：

cpp 复制代码 
struct  结构体名
     {  数据成员表；
         struct  结构体名  *指针变量名；
      }；

3.结点的动态分配

形式是：malloc(存储区字节数)

该函数返回存储区的首地址。

释放存储区用如下函数： free(p)； 它表示释放由p指向的存储空间。

用结构体建立链表：

cpp 复制代码 
struct student
　　｛  int num；
　　　  float score；
　　　  struct student *next ；};

其中成员num和score用来存放结点中的有用数据（用户需要用到的数据），next是指针类型的成员，它指向struct student类型数据（这就是next所在的结构体类型）

二，链表的设计与实现

1.单向链表

1.1 单向链表的组成：

1）头指针

2）结点

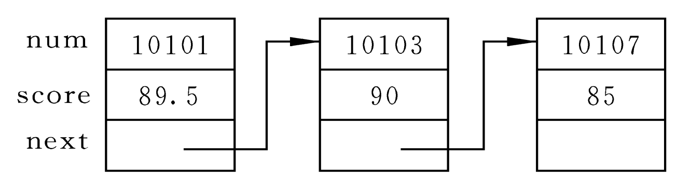
数据域 (保存实际数据)

指针域 (保存下一个结点地址)

1.2 单向链表的设计实现：

1）定义结点类型
cpp 复制代码 
typedef int data_t;
typedef strcut  node
{
	data_t  data;
    strcut node *next;
}node_t;
2）单向链表功能算法实现

(1) 链表创建

int slist_create(node_t**,data_t);

(2) 数据添加

(2.1) 头插

int slist_addhead(node_t**,data_t)

(2.2) 尾插

int slist_addtail(node_t**,data_t)

(2.3) 中间插入

int slist_insert(node_t**,data_t pos,data_t new);

(3) 数据删除

int slist_delete(node_t**,data_t);

(4) 数据查询

node_t* slist_query(node_t*,data_t);

(5) 数据更新

int slist_update(node_t*,data_t old,data_t new);

(6) 数据遍历

void slist_showall(node_t*);

(7) 链表回收

void slist_destroy(node_t**);

1.3 单向链表示例程序

该示例程序涉及到链表创建、数据添加（头插、尾插、中间插入）、数据删除、数据查询、数据更新、数据遍历、链表回收。

slist.c

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef int data_t;

typedef struct node
{
    data_t data;
    struct node *next;
} node_t;

/* 1. 链表创建（创建一个空头指针，返回成功与否） */
int slist_create(node_t **head, data_t value)
{
    *head = (node_t *)malloc(sizeof(node_t));
    if (*head == NULL)
    {
        perror("malloc");
        return -1;
    }
    (*head)->data = value;
    (*head)->next = NULL;
    return 0;
}

/*头插法 */
int slist_addhead(node_t **head, data_t value)
{
    node_t *new = (node_t *)malloc(sizeof(node_t));
    if (!new)
    {
        perror("malloc");
        return -1;
    }
    new->data = value;
    new->next = *head;
    *head = new;
    return 0;
}

/*尾插法 */
int slist_addtail(node_t **head, data_t value)
{
    node_t *new = (node_t *)malloc(sizeof(node_t));
    if (!new)
    {
        perror("malloc");
        return -1;
    }
    new->data = value;
    new->next = NULL;

    if (*head == NULL)
    {
        *head = new;
    }
    else
    {
        node_t *p = *head;
        while (p->next != NULL)
            p = p->next;
        p->next = new;
    }
    return 0;
}

/*中间插入：在指定数据 pos 后插入 new */
int slist_insert(node_t **head, data_t pos, data_t newval)
{
    node_t *p = *head;
    while (p && p->data != pos)
    {
        p = p->next;
    }
    if (!p)
    {
        printf("未找到插入位置 %d\n", pos);
        return -1;
    }

    node_t *new = (node_t *)malloc(sizeof(node_t));
    if (!new)
    {
        perror("malloc");
        return -1;
    }
    new->data = newval;
    new->next = p->next;
    p->next = new;
    return 0;
}

/* 3. 删除结点（按值删除） */
int slist_delete(node_t **head, data_t value)
{
    node_t *p = *head, *q = NULL;
    while (p && p->data != value)
    {
        q = p;
        p = p->next;
    }
    if (!p)
    {
        printf("未找到要删除的值 %d\n", value);
        return -1;
    }

    if (q == NULL)
        *head = p->next; // 删除头结点
    else
        q->next = p->next;

    free(p);
    return 0;
}

/* 4. 查询（返回结点指针） */
node_t *slist_query(node_t *head, data_t value)
{
    while (head)
    {
        if (head->data == value)
            return head;
        head = head->next;
    }
    return NULL;
}

/* 5. 更新 */
int slist_update(node_t *head, data_t old, data_t newval)
{
    node_t *p = slist_query(head, old);
    if (!p)
    {
        printf("未找到需要更新的值 %d\n", old);
        return -1;
    }
    p->data = newval;
    return 0;
}

/* 6. 遍历 */
void slist_showall(node_t *head)
{
    printf("链表内容: ");
    while (head)
    {
        printf("%d -> ", head->data);
        head = head->next;
    }
    printf("NULL\n");
}

/* 7. 链表回收 */
void slist_destroy(node_t **head)
{
    node_t *p = *head;
    while (p)
    {
        node_t *tmp = p;
        p = p->next;
        free(tmp);
    }
    *head = NULL;
}

/* ============= 测试主函数 ============= */
int main(void)
{
    node_t *head = NULL;

    /* 创建链表 */
    slist_create(&head, 10);
    slist_addhead(&head, 5);
    slist_addtail(&head, 20);
    slist_addtail(&head, 30);
    slist_insert(&head, 20, 25); // 在20后插入25
    slist_showall(head);

    /* 删除 */
    slist_delete(&head, 10);
    slist_showall(head);

    /* 查询并更新 */
    node_t *res = slist_query(head, 25);
    if (res)
        printf("找到结点: %d\n", res->data);
    slist_update(head, 25, 99);
    slist_showall(head);

    /* 回收 */
    slist_destroy(&head);
    slist_showall(head);

    return 0;
}

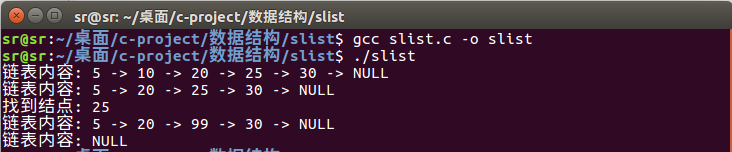
运行结果：

1.4 链表数据结构的小结

应用场景：

1）链式结构是一种动态增加数据的结构，如果存储的数据数量事先无法确定，使用链表是比较合适的;

2）常用于对数据进行频繁的增加或者删除的情况

缺点：

查询效率比较低，主要原因是链表数据必须从头结点开始遍历。

2. 双向链表设计实现

说明：双向链表是在单向链表的基础上，指针域增加了存储上一个结点地址的指针变量(前驱指针)

优势：由于双向链表具有后继指针，也有前驱指针，所以对数据的增加，删除更加方便快捷，原因是链表结点的插入和删除，往往会影响上一个结点，相比于单向链表需要查找上一个结点，双向链表就可以通过结点的前驱指针直接获取。

2.1双向链表的组成

  1. 头指针

  2. 结点：

数据域 (保存实际数据)

指针域 (保存下一个结点地址)

(保存上一个结点地址)

2.2 双向链表的设计实现：

  1. 定义结点类型：
cpp 复制代码 
 typedef int data_t;
 typedef strcut node
 {
  data_t  data;
  strcut  node   *prev;
  strcut  node   *next;
 }node_t;
  1. 双向链表功能算法实现：

（1) 链表创建

int dlist_create(node_t**,data_t);

(2) 数据添加

(2.1) 头插

int dlist_addhead(node_t**,data_t)

(2.2) 尾插

int dlist_addtail(node_t**,data_t)

(2.3) 中间插入

int dlist_insert(node_t** head,data_t pos,data_t new);

(3) 数据删除

int dlist_delete(node_t**,data_t);

(4) 数据查询

node_t* dlist_query(node_t*,data_t);

(5) 数据更新

int dlist_update(node_t*,data_t old,data_t new);

(6) 数据遍历

void dlist_showall(node_t*);

(7) 链表回收

void dlist_destroy(node_t**);

2.3 示例程序：

dlist.c

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef int data_t;

// 定义双向链表结点
typedef struct node {
    data_t data;
    struct node *prev;
    struct node *next;
} node_t;

/*链表创建 */
int dlist_create(node_t **head, data_t value) {
    *head = (node_t *)malloc(sizeof(node_t));
    if (*head == NULL) return -1;

    (*head)->data = value;
    (*head)->prev = NULL;
    (*head)->next = NULL;

    return 0;
}

/*头插 */
int dlist_addhead(node_t **head, data_t value) {
    node_t *newnode = (node_t *)malloc(sizeof(node_t));
    if (newnode == NULL) return -1;

    newnode->data = value;
    newnode->prev = NULL;
    newnode->next = *head;

    if (*head != NULL) {
        (*head)->prev = newnode;
    }
    *head = newnode;

    return 0;
}

/*尾插 */
int dlist_addtail(node_t **head, data_t value) {
    node_t *newnode = (node_t *)malloc(sizeof(node_t));
    if (newnode == NULL) return -1;

    newnode->data = value;
    newnode->next = NULL;

    if (*head == NULL) {
        newnode->prev = NULL;
        *head = newnode;
        return 0;
    }

    node_t *p = *head;
    while (p->next != NULL) {
        p = p->next;
    }
    p->next = newnode;
    newnode->prev = p;

    return 0;
}

/*中间插入（在pos位置前插入新节点） */
int dlist_insert(node_t **head, data_t pos, data_t value) {
    node_t *p = *head;
    while (p != NULL && p->data != pos) {
        p = p->next;
    }
    if (p == NULL) return -1;

    node_t *newnode = (node_t *)malloc(sizeof(node_t));
    if (newnode == NULL) return -1;

    newnode->data = value;
    newnode->next = p;
    newnode->prev = p->prev;

    if (p->prev != NULL) {
        p->prev->next = newnode;
    } else {
        *head = newnode;  // 插在头部
    }
    p->prev = newnode;

    return 0;
}

/*删除节点（删除值为value的第一个节点） */
int dlist_delete(node_t **head, data_t value) {
    node_t *p = *head;
    while (p != NULL && p->data != value) {
        p = p->next;
    }
    if (p == NULL) return -1;

    if (p->prev != NULL) {
        p->prev->next = p->next;
    } else {
        *head = p->next;  // 删除头节点
    }
    if (p->next != NULL) {
        p->next->prev = p->prev;
    }
    free(p);

    return 0;
}

/*数据查询 */
node_t* dlist_query(node_t *head, data_t value) {
    node_t *p = head;
    while (p != NULL) {
        if (p->data == value) {
            return p;
        }
        p = p->next;
    }
    return NULL;
}

/*数据更新 */
int dlist_update(node_t *head, data_t old, data_t new) {
    node_t *p = head;
    while (p != NULL) {
        if (p->data == old) {
            p->data = new;
            return 0;
        }
        p = p->next;
    }
    return -1;
}

/*遍历（正向） */
void dlist_showall(node_t *head) {
    node_t *p = head;
    printf("DList: ");
    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

/*链表回收 */
void dlist_destroy(node_t **head) {
    node_t *p = *head;
    while (p != NULL) {
        node_t *tmp = p;
        p = p->next;
        free(tmp);
    }
    *head = NULL;
}

/* 测试主函数 */
int main() {
    node_t *head = NULL;

    // 创建链表
    dlist_create(&head, 10);
    dlist_addhead(&head, 5);
    dlist_addtail(&head, 20);
    dlist_addtail(&head, 30);
    dlist_insert(&head, 20, 15);  // 在20前插入15
    dlist_showall(head);

    // 查询
    node_t *q = dlist_query(head, 15);
    if (q) printf("Found: %d\n", q->data);

    // 更新
    dlist_update(head, 15, 18);
    dlist_showall(head);

    // 删除
    dlist_delete(&head, 10);
    dlist_showall(head);

    // 回收
    dlist_destroy(&head);
    return 0;
}

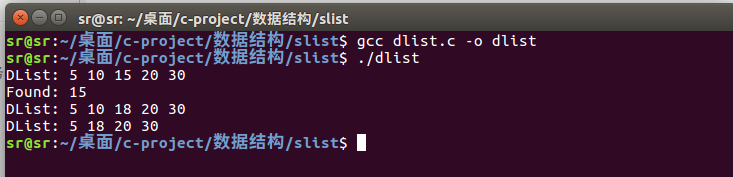
运行结果：

链表小结：

1. 定义

  • 单向链表（Singly Linked List）

    每个节点只有一个指针 next，指向下一个节点。

    结构简单，内存开销小，但只能 单方向遍历。

  • 双向链表（Doubly Linked List）

    每个节点有两个指针：prev（前驱）和 next（后继）。

    可以 双向遍历，删除/插入更方便，但每个节点占用内存更大。

2. 节点结构

单向链表

cpp 复制代码 
typedef int data_t;
typedef struct node {
    data_t data;
    struct node *next;
} node_t;

双向链表

cpp 复制代码 
typedef int data_t;
typedef struct node {
    data_t data;
    struct node *prev;
    struct node *next;
} node_t;

3. 基本功能函数

功能 单向链表 (slist) 双向链表 (dlist)
创建链表 slist_create() dlist_create()
头插入 slist_addhead() dlist_addhead()
尾插入 slist_addtail() dlist_addtail()
中间插入 slist_insert() dlist_insert()
删除节点 slist_delete() dlist_delete()
查询节点 slist_query() dlist_query()
更新节点 slist_update() dlist_update()
遍历输出 slist_showall() (等同于 print) dlist_showall() (等同于 print)
销毁链表 slist_destroy() dlist_destroy()

4. 主要区别

对比点 单向链表 双向链表
内存占用 小，每个节点只需 next 指针 大，每个节点需 prev + next
遍历方向 只能从头到尾 可从头到尾，也能从尾到头
插入效率 需要找到插入点的前驱节点 直接利用 prev / next 修改指针，效率更高
删除效率 需要找到删除节点的前驱节点 直接用 prev / next 修改即可
实现复杂度 简单 稍复杂
适用场景 内存紧张、简单队列/栈结构 频繁插入/删除、需要双向遍历

5. 输出函数

单向链表输出

cpp 复制代码 
void slist_showall(node_t* head) {
    node_t* p = head;
    while (p) {
        printf("%4d\n", p->data);  // 每行一个，右对齐
        p = p->next;
    }
}

双向链表输出

cpp 复制代码 
void dlist_showall(node_t* head) {
    node_t* p = head;
    while (p) {
        printf("%4d\n", p->data);
        p = p->next;
    }
}

总结：

  • 单向链表：结构简单，适合空间敏感、逻辑简单的场景（如栈、队列）。

  • 双向链表：操作灵活，适合需要频繁插入/删除和双向遍历的场景（如 LRU 缓存、双端队列）。

相关推荐
jinmo_C++41 分钟前
数据结构_ 二叉树线索化：从原理到手撕实现
数据结构
钮钴禄·爱因斯晨3 小时前
数据结构|图论：从数据结构到工程实践的核心引擎
c语言·数据结构·图论
向前阿、4 小时前
数据结构从入门到实战————栈
c语言·开发语言·数据结构·程序人生
洲覆5 小时前
Redis 64字节分界线与跳表实现原理
数据结构·数据库·redis·缓存
im_AMBER5 小时前
数据结构 02 线性表
数据结构·算法
-雷阵雨-5 小时前
数据结构——包装类&&泛型
java·开发语言·数据结构·intellij-idea
gsfl5 小时前
redis常见数据结构及其编码方式
数据结构·redis
im_AMBER6 小时前
数据结构 01 线性表
数据结构·学习
_码力全开_6 小时前
Python从入门到实战 (14)：工具落地：用 PyInstaller 打包 Python 脚本为可执行文件
开发语言·数据结构·python·个人开发
Keying,,,,7 小时前
秋招算法记录 | 排序算法整理 | 直接选择、直接插入、冒泡、快排、希尔排序
数据结构·python·算法·排序算法
热门推荐
01GitHub 镜像站点02UV 工具安装与国内镜像源配置指南03UV安装并设置国内源04Spec-Kit 使用指南05阿里最新开源Wan2.2-Animate-14B 本地部署教程：统一双模态框架，MoE架构赋能电影级角色动画与替换06OpenSpeedy简介07Linux下V2Ray安装配置指南08KGG转MP3工具|非KGM文件|解密音频0946个Nano-banana 精选提示词，持续更新中10VsCode远程Copilot无法使用Claude Agent问题