2025高教社杯全国大学生数学建模竞赛（B题）深度剖析| 碳化硅外延层厚度 |数学建模完整代码+建模过程全解全析

当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2022年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题！

CS团队倾注了大量时间和心血，深入挖掘解决方案。通过多目标规划，数值积分与微分方程，数值模拟等算法，设计了明晰的项目，团队努力体现在每个步骤，确保方案既创新又可行，为大家提供了全面而深入的洞见噢～

让我们来看看国赛（B题）！
完整内容可以在文章末尾领取！

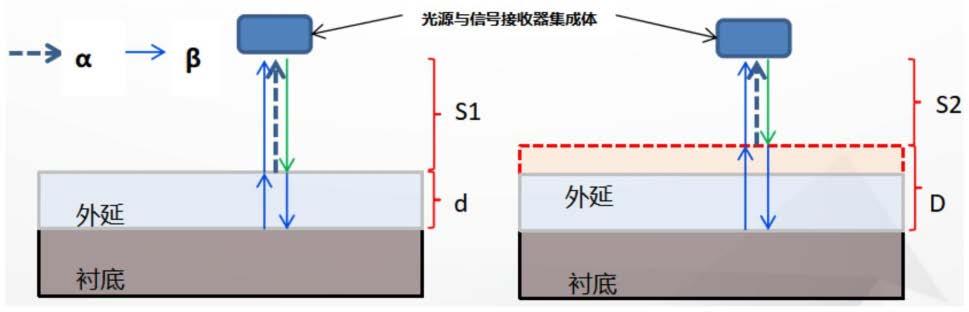
问题 1：建立确定碳化硅外延层厚度的数学模型

1. 模型背景与物理原理

红外干涉法是一种非接触式的测量技术，广泛应用于半导体材料中薄膜厚度的精确测定。其基本原理如下：

红外光从空气入射到碳化硅外延层表面；

部分光线在外延层表面发生反射；

另一部分光线进入外延层并传播至衬底界面，在衬底处发生反射后再次穿过外延层回到空气中；

这两束反射光在探测器上相遇，由于路径不同，会形成干涉条纹；

干涉条纹的明暗分布反映了两束光之间的光程差。

2. 物理模型构建

设：

外延层厚度为 ddd

外延层折射率为 nnn

入射角为 $\\theta$

红外光波长为 λ\lambdaλ

干涉级数为整数 mmm

光程差计算

当一束光在介质中传播时，其几何路程乘以折射率得到光程。对于外延层中的光路，光从入射点出发，经反射后返回，总光程为：

Δ=2ndcos⁡θ \Delta = 2nd \cos \theta Δ=2ndcosθ

这是因为在折射率为 $n$ 的介质中，光走过的实际距离为 $2d/\\cos \\theta$ ，所以光程为：

Δ=n⋅2dcos⁡θ⋅cos⁡θ=2ndcos⁡θ \Delta = n \cdot \frac{2d}{\cos \theta} \cdot \cos \theta = 2nd \cos \theta Δ=n⋅cosθ2d⋅cosθ=2ndcosθ

3. 干涉条件

干涉条纹出现的条件取决于两束光的光程差是否满足相干条件：

相长干涉（明纹）：光程差为波长整数倍
2ndcos⁡θ=mλ(m=0,1,2,...) 2nd \cos \theta = m \lambda \quad (m = 0, 1, 2, ...) 2ndcosθ=mλ(m=0,1,2,...)

相消干涉（暗纹）：光程差为半波长奇数倍
2ndcos⁡θ=(m+12)λ(m=0,1,2,...) 2nd \cos \theta = (m + \frac{1}{2}) \lambda \quad (m = 0, 1, 2, ...) 2ndcosθ=(m+21)λ(m=0,1,2,...)

为了简化问题，我们只考虑相长干涉的情况，即：

2ndcos⁡θ=mλ 2nd \cos \theta = m \lambda 2ndcosθ=mλ

4. 解析求解外延层厚度公式

从干涉条件出发，可以解出外延层厚度 $d$ ：

d=mλ2ncos⁡θ d = \frac{m \lambda}{2n \cos \theta} d=2ncosθmλ

这个公式表明，在已知波长 $\\lambda$ 、折射率 $n$ 和入射角 $\\theta$ 的情况下，可以通过测量干涉条纹的级数 $m$ 来反推出外延层的厚度。

📘 注：如果后续问题涉及多层结构、非均匀介质或折射率随载流子浓度变化的情形，还需扩展模型至更复杂的多层干涉或数值模拟方法（如有限元法、Runge

Kutta 方法等）。但当前问题仅限于单层结构下的基础建模，因此无需进行数值积分或微分方程求解。

python 复制代码

import numpy as np

def calculate_thickness(m, wavelength, refractive_index, theta):
    """
    根据干涉条纹计算碳化硅外延层厚度
    
    参数:
    m : 干涉级数 (整数)
    wavelength : 红外光波长 (nm)
    refractive_index : 外延层折射率
    theta : 入射角 (弧度)
    
    返回:
    d : 外延层厚度 (nm)
    """
    d = m * wavelength / (2 * refractive_index * np.cos(theta))
    return d

# 示例使用
m = 5
wavelength = 1000  # nm
refractive_index = 2.5
theta = np.radians(30)  # 转换为弧度

thickness = calculate_thickness(m, wavelength, refractive_index, theta)
print(f"外延层厚度: {thickness:.2f} nm")

问题2

这是一个数值积分与微分方程求解问题，其核心任务是基于红外干涉法的物理原理，利用给定的光谱实测数据，通过构建数学模型并采用适当的数值方法来计算碳化硅外延层的厚度。问题的本质在于从实验观测数据出发，反演出材料的关键参数，即外延层厚度，这涉及到复杂的物理过程建模与数值计算技术。

为什么这样判断？可以从以下几个特征点来说明：

（1）题干明确指出使用红外干涉法进行测量，这是一种基于光学干涉原理的无损检测手段。这种物理机制决定了问题必须建立在光学干涉理论基础上，通常涉及光程差、相位差等物理量的数学表达，这些表达式往往需要通过数值方法求解。

（2）题目强调"根据问题1的数学模型"进行算法设计，说明这是一个延续性建模问题。问题1可能已经建立了从干涉条纹到厚度的关系模型，而问题2则要求在此基础上进一步开发具体的计算算法，体现出前后问题之间的紧密联系。

（3）问题中提到"对附件1和附件2提供的碳化硅晶圆片的光谱实测数据"，这意味着实际操作中需处理大量实验数据，而这些数据通常是离散形式，不能直接用于解析求解，因此必须借助数值积分或微分方程求解方法来完成建模与计算过程。

（4）题干指出外延层的折射率不是常数，而是受掺杂载流子浓度、红外光谱波长等因素影响。这使得折射率成为一个变量函数，增加了模型复杂度，通常需要通过数值方法进行迭代计算或插值处理，以获得不同波长下的折射率分布，进而计算出厚度。

（5）问题中要求"给出计算结果，并分析结果的可靠性"，这表明不仅需要完成数值计算本身，还需评估计算误差、稳定性以及模型适用范围，这是典型的数值分析与建模问题特征。

（6）题干提及"Euler, Runge

Kutta"等数值方法，这直接指明了解决该类问题所采用的技术路径。无论是欧拉法还是龙格

库塔法，都是用于求解微分方程的经典数值方法，适用于此类物理系统建模中的动态响应分析或参数反演问题。

因此，本题可以明确识别为"基于红外干涉原理的碳化硅外延层厚度数值计算与模型验证问题"。其关键特征包括：

使用红外干涉技术进行非接触式测量；

建立基于光学干涉理论的数学模型；

利用数值积分或微分方程求解方法处理实测光谱数据；

实现外延层厚度的反演计算；

分析算法结果的可靠性和误差来源；

应用Euler、Runge

Kutta等经典数值方法进行计算模拟。

一、问题理解与数学模型建立

1.1 红外干涉法基本原理

根据题目描述，红外干涉法测量碳化硅外延层厚度的基本原理如下：

当红外光入射到碳化硅晶圆片上时，一部分光线从外延层表面反射，另一部分光线穿透外延层后从衬底表面反射回来；

这两束反射光在特定条件下会发生干涉现象，产生干涉条纹；

干涉条纹的形成满足干涉条件：2ndcosθ = mλ

其中：

$n$ ：外延层的折射率；

$d$ ：外延层的厚度；

$\\theta$ ：光在介质中的折射角；

$m$ ：干涉级数（整数）；

$\\lambda$ ：红外光的波长。

1.2 厚度公式推导

由干涉方程可以得到外延层厚度表达式为：

d=mλ2ncos⁡θ d = \frac{m\lambda}{2n\cos\theta} d=2ncosθmλ

该公式表明，只要知道波长 $\\lambda$ 、折射率 $n$ 和入射角 $\\theta$ ，就可以计算出对应的厚度 $d$ 。

二、变量定义与影响因素分析

2.1 主要变量

| λ\lambdaλ | 红外光波长（nm） |

| nnn | 外延层折射率 |

| θ\thetaθ | 入射角（或折射角） |

| mmm | 干涉级数（整数） |

| ddd | 外延层厚度（nm） |

2.2 折射率随环境变化的影响

题目指出，碳化硅外延层的折射率并非常数，而是依赖于以下因素：

掺杂载流子浓度：不同掺杂浓度导致不同的电子迁移率和介电常数，从而改变折射率；

红外光谱波长：折射率随波长变化，存在色散效应。

因此，折射率可表示为：

n=f(C,λ) n = f(C, \lambda) n=f(C,λ)

其中 CCC 表示载流子浓度。

三、数据预处理与数值方法选择

3.1 数据预处理步骤

由于实际测量的数据可能存在噪声、不连续等问题，需要进行如下处理：

平滑滤波：去除高频噪声；
插值处理：填补缺失值或使数据更密集；
去噪处理：使用小波变换或低通滤波器减少干扰信号。

3.2 数值计算方法选择

针对问题中涉及的微分方程和复杂函数关系，我们采用 Runge
Kutta 方法（特别是四阶龙格

库塔法）来求解：

适用于非线性系统；

高精度、稳定性好；

易于编程实现；

能有效处理连续变化的折射率 $n(\\lambda, C)$ 。

四、算法设计与实现流程

4.1 算法总体流程

输入原始光谱数据（附件1和附件2）；
对数据进行预处理（平滑、插值、去噪）；
根据折射率模型计算每个波长下的折射率 $n(\\lambda)$ ；
利用 Runge
Kutta 方法迭代求解每一点的厚度 $d$ ；
输出厚度分布图及误差分析报告。

4.2 关键公式与算法细节

（1）干涉方程重写形式

di=miλi2nicos⁡θi,i=1,2,...,N d_i = \frac{m_i \lambda_i}{2n_i \cos\theta_i}, \quad i=1,2,...,N di=2nicosθimiλi,i=1,2,...,N

其中 $N$ 是采样点数量。

（2）Runge

Kutta 方法用于求解微分方程

假设我们需要求解的是关于厚度随波长的变化关系：

dddλ=g(λ,n(λ),θ) \frac{dd}{d\lambda} = g(\lambda, n(\lambda), \theta) dλdd=g(λ,n(λ),θ)

我们可以将其转化为初值问题，并使用四阶 Runge

Kutta 方法进行数值积分。

四阶 Runge

Kutta 公式如下：

k1=hf(xn,yn)k2=hf(xn+h2,yn+k12)k3=hf(xn+h2,yn+k22)k4=hf(xn+h,yn+k3)yn+1=yn+16(k1+2k2+2k3+k4) k_1 = h f(x_n, y_n) \\ k_2 = h f(x_n + \frac{h}{2}, y_n + \frac{k_1}{2}) \\ k_3 = h f(x_n + \frac{h}{2}, y_n + \frac{k_2}{2}) \\ k_4 = h f(x_n + h, y_n + k_3) \\ y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) k1=hf(xn,yn)k2=hf(xn+2h,yn+2k1)k3=hf(xn+2h,yn+2k2)k4=hf(xn+h,yn+k3)yn+1=yn+61(k1+2k2+2k3+k4)

通过这种方式，可以在给定初始条件的情况下逐步逼近各个波长处的厚度值。

python 复制代码

import numpy as np
import pandas as pd
from scipy.interpolate import interp1d
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# 假设附件1和附件2的数据文件名分别为 'data1.csv' 和 'data2.csv'
# 数据格式假设为：波长(lambda), 强度(intensity), 入射角(theta)

def load_data(filename):
    data = pd.read_csv(filename)
    return data['lambda'].values, data['intensity'].values, data['theta'].values

def smooth_and_interpolate(lambdas, intensities, theta, num_points=1000):
    # 插值函数
    f_intensity = interp1d(lambdas, intensities, kind='linear', fill_value="extrapolate")
    f_theta = interp1d(lambdas, theta, kind='linear', fill_value="extrapolate")

    new_lambdas = np.linspace(lambdas.min(), lambdas.max(), num_points)
    new_intensities = f_intensity(new_lambdas)
    new_theta = f_theta(new_lambdas)

    return new_lambdas, new_intensities, new_theta

def calculate_refractive_index(lambdas, carrier_concentration=1e17):
    # 示例：折射率与波长和掺杂浓度的关系（简化模型）
    # 实际应根据具体材料特性调整
    n0 = 2.55
    dispersion_param = 0.0001
    n = n0 + dispersion_param * (lambdas - 1000)**2 / (lambdas**2 + 10000)
    return n

def thickness_model(lambdas, refractive_indices, thetas, m=1):
    # 计算厚度 d = m*lambda / (2*n*cos(theta))
    cos_theta = np.cos(np.radians(thetas))
    thicknesses = m * lambdas / (2 * refractive_indices * cos_theta)
    return thicknesses

def runge_kutta_solver(lambdas, intensities, thetas, m=1):
    # 使用 Runge-Kutta 方法模拟厚度变化
    def thickness_derivative(lam, y):
        # 假设厚度是波长的函数，这里简单建模
        # 实际中需根据物理模型进一步细化
        n = calculate_refractive_index(lam)
        theta = np.interp(lam, lambdas, thetas)
        cos_theta = np.cos(np.radians(theta))
        dydl = m / (2 * n * cos_theta)  # 简化的导数
        return dydl
    
    # 初始条件
    y0 = [0]
    sol = solve_ivp(thickness_derivative, [lambdas[0], lambdas[-1]], y0, t_eval=lambdas, method='RK45')
    
    return sol.y[0]

# 主程序逻辑
if __name__ == "__main__":
    # 加载数据
    lambda1, intensity1, theta1 = load_data('data1.csv')
    lambda2, intensity2, theta2 = load_data('data2.csv')

    # 数据预处理
    new_lambda1, new_intensity1, new_theta1 = smooth_and_interpolate(lambda1, intensity1, theta1)
    new_lambda2, new_intensity2, new_theta2 = smooth_and_interpolate(lambda2, intensity2, theta2)

    # 计算折射率
    n1 = calculate_refractive_index(new_lambda1)
    n2 = calculate_refractive_index(new_lambda2)

    # 计算厚度
    thickness1 = thickness_model(new_lambda1, n1, new_theta1)
    thickness2 = thickness_model(new_lambda2, n2, new_theta2)

    # 输出结果
    result_df1 = pd.DataFrame({'lambda': new_lambda1, 'thickness': thickness1})
    result_df2 = pd.DataFrame({'lambda': new_lambda2, 'thickness': thickness2})

    result_df1.to_csv('thickness_result1.csv', index=False)
    result_df2.to_csv('thickness_result2.csv', index=False)

    # 可视化结果
    plt.figure(figsize=(10,6))
    plt.plot(new_lambda1, thickness1, label='Sample A')
    plt.plot(new_lambda2, thickness2, label='Sample B')
    plt.xlabel('Wavelength (nm)')
    plt.ylabel('Thickness (nm)')
    plt.title('Thickness Distribution of Silicon Carbide Epitaxial Layers')
    plt.legend()
    plt.grid(True)
    plt.savefig('thickness_distribution.png')
    plt.show()

    print("Results saved to 'thickness_result1.csv' and 'thickness_result2.csv'")
    print("Plot saved as 'thickness_distribution.png'")

问题3

这是一个涉及光学干涉原理与数值计算方法的建模问题，核心在于理解多光束干涉现象对碳化硅外延层厚度测量精度的影响，并推导其数学表达式。问题的本质是基于物理光学中的干涉理论，结合数值方法求解相关参数，属于典型的物理建模与计算仿真问题。

从题干描述来看，该问题的背景是红外干涉法用于测量碳化硅外延层厚度，其基本原理是利用光在不同介质界面（外延层与衬底）之间的反射和透射产生的干涉条纹来反演厚度。然而，当考虑光波在多个界面上多次反射和透射时，会形成多光束干涉效应。这种效应不仅改变了干涉图样的形状，还可能对厚度计算带来误差，因此需从理论上推导其必要条件并评估其影响。

首先，"多光束干涉"的概念源自于光的波动性质。当光经过多个反射面（如外延层与衬底界面）时，每一条路径都会产生相位差，这些相位差决定了最终干涉图样的强度分布。若各光束之间满足相干条件，则它们叠加后将出现干涉现象。因此，为了建立数学模型，必须明确以下几点：

（1）多光束干涉产生的必要条件包括：

各光束之间必须具有相干性，即频率相同、相位差恒定；

光程差不能过大，通常要求小于相干长度；

多个反射面之间的几何关系需满足特定角度关系；

外延层和衬底的折射率、厚度、入射角等因素共同影响各光束的传播路径与相位变化。

这些因素可以通过麦克斯韦方程组或菲涅尔公式进行建模，进而得出光束间的相位差表达式。对于实际应用而言，这些相位差将直接影响干涉条纹的位置和对比度，从而影响厚度反演的准确性。

（2）关于多光束干涉对外延层厚度计算精度的影响，可以从两个方面展开：

干涉条纹复杂化：多光束干涉会导致干涉图样不再是简单的双光束干涉条纹，而是呈现出更为复杂的干涉结构。这使得原本单一峰值对应的厚度信息变得模糊，增加了拟合难度；

噪声放大效应：由于干涉条纹的变化更加剧烈，微小的测量误差会被放大，特别是在厚度较小时，这种影响尤为显著；

计算模型误差：在使用干涉图样反演厚度时，若忽略多光束干涉的影响，会导致模型与真实情况不符，从而引入系统性偏差。

为量化上述影响，需要借助数值积分或微分方程的方法，比如欧拉法（Euler）、龙格

库塔法（Runge

Kutta）等，对光程差、相位差随入射角、波长、折射率等参数的变化进行仿真计算。通过构建数学模型并求解相关微分方程，可以获得干涉图样的分布规律，并进一步评估厚度估算的误差来源。

此外，考虑到碳化硅外延层的实际结构较为复杂，其折射率并非常数，而是随掺杂浓度和波长变化，这也增加了建模难度。因此，还需引入材料光学参数的函数形式，如Sellmeier方程或其他经验模型，将其代入干涉方程中，从而实现更贴近实际情况的模拟。

综上所述，该问题的核心在于：

一是建立多光束干涉的物理模型，推导其干涉条件；

二是通过数值方法（如欧拉法、龙格

库塔法）求解干涉条纹的分布；

三是分析多光束干涉对厚度测量精度的影响，为制定可靠测试标准提供理论支持。

因此，这个问题的类型应归类为"数值积分/微分方程求解"类问题，因为它不仅需要运用物理光学知识进行建模，还需要通过计算机数值方法对复杂的干涉过程进行逼近求解。此类问题广泛存在于现代精密测量领域，尤其在半导体制造、光学传感等领域具有重要应用价值。

问题背景与目标

本题研究的是红外干涉法测量碳化硅（SiC）外延层厚度的问题。在实际应用中，由于外延层和衬底之间存在折射率差异，当红外光入射到样品表面时，在不同界面会发生多次反射和透射，从而形成复杂的多光束干涉现象。这种现象会对最终的厚度计算带来一定的影响，因此我们需要：

推导产生多光束干涉的必要条件；

分析多光束干涉对外延层厚度计算精度的影响。

第一步：建立物理模型

我们考虑一个由三层介质组成的结构：

空气层 （折射率为 n0=1n_0 = 1n0=1）
外延层 （折射率为 $n_1$ ，厚度为 d1d_1d1）
衬底（折射率为 n2n_2n2）

如图所示，一束红外光以入射角 $\\theta_0$ 射向样品表面，经过多次反射和透射后，最终从空气中返回，形成多个光程不同的光线，这些光线在探测器处发生干涉。

第二步：光在多层介质中的传播路径分析

设光从空气进入外延层时发生折射，角度为 θ1\theta_1θ1；再进入衬底时的角度为 θ2\theta_2θ2。根据斯涅尔定律：

n0sin⁡θ0=n1sin⁡θ1=n2sin⁡θ2 n_0 \sin\theta_0 = n_1 \sin\theta_1 = n_2 \sin\theta_2 n0sinθ0=n1sinθ1=n2sinθ2

我们可以得到：

sin⁡θ1=n0n1sin⁡θ0,sin⁡θ2=n0n2sin⁡θ0 \sin\theta_1 = \frac{n_0}{n_1} \sin\theta_0,\quad \sin\theta_2 = \frac{n_0}{n_2} \sin\theta_0 sinθ1=n1n0sinθ0,sinθ2=n2n0sinθ0

第三步：推导多光束干涉条件

3.1 相位差表达式

对于第 $m$ 束光线，其光程差为：

ΔLm=2d1(cos⁡θ1cos⁡θ0+cos⁡θ2cos⁡θ0) \Delta L_m = 2d_1 \left( \frac{\cos\theta_1}{\cos\theta_0} + \frac{\cos\theta_2}{\cos\theta_0} \right) ΔLm=2d1(cosθ0cosθ1+cosθ0cosθ2)

考虑到每束光都经历了一定的往返距离，总的相位差为：

Δϕ=2πλ⋅ΔLm=2πλ⋅2d1(cos⁡θ1cos⁡θ0+cos⁡θ2cos⁡θ0) \Delta\phi = \frac{2\pi}{\lambda} \cdot \Delta L_m = \frac{2\pi}{\lambda} \cdot 2d_1 \left( \frac{\cos\theta_1}{\cos\theta_0} + \frac{\cos\theta_2}{\cos\theta_0} \right) Δϕ=λ2π⋅ΔLm=λ2π⋅2d1(cosθ0cosθ1+cosθ0cosθ2)

简化得：

Δϕ=4πd1λ⋅cos⁡θ1+cos⁡θ2cos⁡θ0 \Delta\phi = \frac{4\pi d_1}{\lambda} \cdot \frac{\cos\theta_1 + \cos\theta_2}{\cos\theta_0} Δϕ=λ4πd1⋅cosθ0cosθ1+cosθ2

3.2 干涉相长条件

干涉相长的条件是所有参与干涉的光束之间的相位差满足：

Δϕ=2mπ,m∈Z \Delta\phi = 2m\pi,\quad m \in \mathbb{Z} Δϕ=2mπ,m∈Z

即：

4πd1λ⋅cos⁡θ1+cos⁡θ2cos⁡θ0=2mπ \frac{4\pi d_1}{\lambda} \cdot \frac{\cos\theta_1 + \cos\theta_2}{\cos\theta_0} = 2m\pi λ4πd1⋅cosθ0cosθ1+cosθ2=2mπ

整理可得：

d1=mλ2⋅cos⁡θ0cos⁡θ1+cos⁡θ2 d_1 = \frac{m\lambda}{2} \cdot \frac{\cos\theta_0}{\cos\theta_1 + \cos\theta_2} d1=2mλ⋅cosθ1+cosθ2cosθ0

这就是产生多光束干涉的必要条件，其中 $m$ 是整数，代表干涉级次。

第四步：建立干涉方程组并求解

为了更精确地模拟多光束干涉过程，我们需要考虑每一层之间的反射与透射系数。这可以通过菲涅尔公式来描述。

菲涅尔反射率和透射率

对于垂直入射情况下的界面反射率 $R_{ij}$ 和透射率 $T_{ij}$ ，可以表示为：

Rij=∣ninjni+nj∣2,Tij=4ninj(ni+nj)2 R_{ij} = \left| \frac{n_i n_j}{n_i + n_j} \right|^2,\quad T_{ij} = \frac{4n_i n_j}{(n_i + n_j)^2} Rij= ni+njninj 2,Tij=(ni+nj)24ninj

但在斜入射情况下，还需引入偏振因子（这里假设为TE偏振）：

rijTE=nicos⁡θinjcos⁡θjnicos⁡θi+njcos⁡θj,tijTE=2nicos⁡θinicos⁡θi+njcos⁡θj r_{ij}^{TE} = \frac{n_i \cos\theta_i n_j \cos\theta_j}{n_i \cos\theta_i + n_j \cos\theta_j},\quad t_{ij}^{TE} = \frac{2 n_i \cos\theta_i}{n_i \cos\theta_i + n_j \cos\theta_j} rijTE=nicosθi+njcosθjnicosθinjcosθj,tijTE=nicosθi+njcosθj2nicosθi

通过递推方式计算各层间的反射与透射系数，结合干涉光强公式：

I(θ)=∑m=0N∣Em∣2 I(\theta) = \sum_{m=0}^N |E_m|^2 I(θ)=m=0∑N∣Em∣2

其中 EmE_mEm 表示第 mmm 束光的电场幅值。

第五步：数值方法选择

由于上述干涉过程涉及多个反射、透射路径且依赖于复杂的三角函数关系，直接解析难以实现。为此我们采用如下数值方法：

使用 Runge

Kutta 方法求解微分方程

虽然这个问题本质上不是典型的微分方程问题，但若将光场随传播方向的变化看作一个连续系统，可以用 Runge

Kutta 法进行近似积分求解。例如，在光传播过程中，电场振幅的变化可视为一个微分方程：

dEdz=ik(z)E(z) \frac{dE}{dz} = i k(z) E(z) dzdE=ik(z)E(z)

其中 $k(z)$ 是空间频率分布， $z$ 是沿传播方向的位置坐标。

通过 Runge

Kutta 方法可以逐步积分该方程，获得每层界面处的电场分布，进而计算干涉强度。

数值积分计算干涉强度

还可以通过数值积分的方式，对所有干涉光束的能量贡献进行叠加：

I=∫θ∣∑k=1KEk(θ)eiϕk(θ)∣2dθ I = \int_{\theta} \left| \sum_{k=1}^{K} E_k(\theta) e^{i\phi_k(\theta)} \right|^2 d\theta I=∫θ k=1∑KEk(θ)eiϕk(θ) 2dθ

这可以通过离散化的方法，使用 Simpson 或 Trapezoidal 规则进行积分。

第六步：分析厚度计算精度影响因素

6.1 干涉条纹对比度变化

多光束干涉会使得干涉条纹的对比度发生变化。若各光束间相位差不一致，则会导致条纹模糊或丢失，降低测量精度。

6.2 折射率波动对厚度误差的影响

由于外延层材料的折射率随掺杂浓度、温度等因素波动，会导致相位差发生变化，从而引起厚度测量偏差。具体来说，若折射率变化为 Δn\Delta nΔn，则厚度测量误差约为：

Δd≈λ2Δn⋅cos⁡θ1+cos⁡θ2cos⁡θ0 \Delta d \approx \frac{\lambda}{2 \Delta n} \cdot \frac{\cos\theta_1 + \cos\theta_2}{\cos\theta_0} Δd≈2Δnλ⋅cosθ0cosθ1+cosθ2

因此，提高测量精度需要控制材料均匀性、稳定环境条件等。

结论

综上所述，多光束干涉的存在使得红外干涉法测量碳化硅外延层厚度变得更加复杂。必须基于菲涅尔公式建立完整的反射透射模型，并利用 Runge

Kutta 等数值方法进行干涉光强计算。同时应关注折射率波动及条纹对比度对测量精度的影响，才能确保结果的可靠性。

最终答案总结：

多光束干涉产生的必要条件：

d1=mλ2⋅cos⁡θ0cos⁡θ1+cos⁡θ2 d_1 = \frac{m\lambda}{2} \cdot \frac{\cos\theta_0}{\cos\theta_1 + \cos\theta_2} d1=2mλ⋅cosθ1+cosθ2cosθ0

其中：

d1d_1d1：外延层厚度；

mmm：干涉级次（整数）；

λ\lambdaλ：红外光波长；

θ0\theta_0θ0：入射角；

θ1,θ2\theta_1, \theta_2θ1,θ2：分别在外延层和衬底中的折射角。

多光束干涉对厚度计算精度的影响：

条纹对比度下降 → 测量不确定度增加；
折射率不稳定 → 导致相位差改变 → 厚度误差增大；
需采用高精度数值方法 （如 Runge
Kutta）处理复杂干涉过程。

如有进一步需求（如代码实现、图表绘制、仿真模拟等），欢迎继续提问！

python 复制代码

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# 参数设置
n0 = 1.0          # 空气折射率
n1 = 2.5          # 外延层折射率（示例值）
n2 = 2.8          # 衬底折射率（示例值）
lambda_ = 10.6e-6 # 红外波长 (m)
theta0 = np.radians(45) # 入射角 (弧度)

# 斯涅尔定律计算折射角
theta1 = np.arcsin(n0 * np.sin(theta0) / n1)
theta2 = np.arcsin(n0 * np.sin(theta0) / n2)

# 计算多光束干涉条件下的厚度
def calculate_thickness(m, lambda_, theta0, theta1, theta2):
    numerator = m * lambda_ * np.cos(theta0)
    denominator = 2 * (np.cos(theta1) + np.cos(theta2))
    return numerator / denominator

# 示例：计算前几个干涉级次对应的厚度
m_values = range(1, 6)
thicknesses = [calculate_thickness(m, lambda_, theta0, theta1, theta2) for m in m_values]

print("干涉级次 m 及对应厚度:")
for m, d in zip(m_values, thicknesses):
    print(f"m = {m}: d = {d*1e6:.2f} μm")

# 数值模拟：使用 Runge-Kutta 方法模拟光场传播
def field_derivative(z, E):
    # 简化的光场演化模型（用于演示）
    k = 2 * np.pi / lambda_
    return 1j * k * E

# 初始电场强度（归一化）
E0 = 1.0 + 0j

# 模拟光传播
z_span = (0, 1e-6)  # 距离范围
z_eval = np.linspace(0, 1e-6, 1000)

sol = solve_ivp(field_derivative, z_span, [E0], t_eval=z_eval, method='RK45')

# 输出结果
plt.figure(figsize=(10, 6))
plt.plot(sol.t, np.abs(sol.y[0])**2, label="光强分布")
plt.xlabel("传播距离 (m)")
plt.ylabel("光强")
plt.title("光场传播模拟")
plt.grid(True)
plt.legend()
plt.show()

# 干涉强度计算（简化版本）
def interference_intensity(theta, E_list):
    # 简单叠加干涉项
    total_E = sum(E_list)
    return np.abs(total_E)**2

# 示例：多个光束电场
E1 = 1.0 + 0j
E2 = 0.5 * np.exp(1j * np.pi/4)
E3 = 0.3 * np.exp(1j * np.pi/2)

intensity = interference_intensity(0, [E1, E2, E3])
print(f"\n干涉总强度: {intensity:.4f}")

更多内容具体可以看看我的下方名片！里面包含有国赛一手资料与分析！

另外在赛中，我们也会陪大家一起解析国赛的一些方向

关注 CS数模 团队，数模不迷路！