2025亚太杯APMCM数学建模竞赛选题建议
提示:认为难度:B题(中)< C题(中)< A题(高)< D题(高),开放度: D题(中)< A题(中)< B题(高)< C题(高)。B题和C题基于标准学科知识,A题和D题需处理复杂系统或先进概念。D题和A题有较多约束,B题和C题在模型设计和数据使用上更自由。
通过网盘分享的文件:资料分享
链接: https://pan.baidu.com/s/1OICSbGnbLkvuVzQ_flsM5w?pwd=u5eg 提取码: u5eg

- A题(机器人性能优化):聚焦机器人运动规划、关节角度计算、轨迹优化和能量消耗,需要结合运动学和动力学建模。
- B题(辐射冷却技术建模与优化):涉及材料物理特性、热力学和电磁学,要求优化薄膜结构以实现被动冷却。
- C题(美国关税政策对全球贸易和区域经济的影响):基于真实贸易数据,分析关税政策的经济影响,需构建计量经济或均衡模型。
- D题(电力系统 中基于量子的机组组合问题优化):将传统电力系统优化问题转化为量子计算** 形式,涉及混合整数规划和量子算法。**
专业选题:

A题:机器人性能优化(Problem A: Optimization of Robot's Performance)
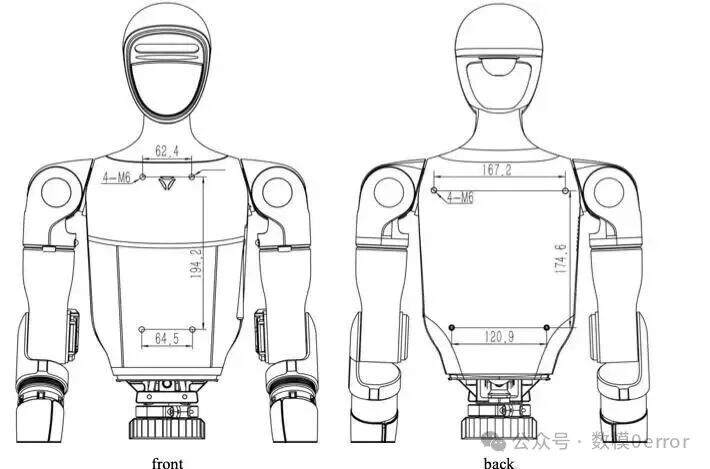
A题聚焦优化人形机器人的性能,包括关节角度计算、运动轨迹规划、多关节协同和能量消耗。问题基于真实场景(如舞蹈表演),强调电机安全和重心稳定性。题目涉及多体动力学和实时控制,难度较高,需综合运动学、优化理论和安全约束。第一问具体是计算机器人左端点坐标,给定手臂长度和角度。
部分第一问建模过程:

推荐算法:
-
前沿算法
:深度强化学习(DRL),如近端策略优化(PPO),用于实时轨迹优化;或元启发式算法如多目标粒子群优化(MOPSO),平衡能量消耗和稳定性。这些算法能处理非线性约束,优于传统PID。
-
理由
:DRL可从仿真中学习安全策略,MOPSO适用于多目标优化(如最小化能量和最大稳定性)。
-
推荐可视化方法
-
前沿可视化
:交互式3D运动仿真(如用Unity或Python的Plotly),动态显示机器人关节角度和轨迹;或热图可视化能量消耗分布。这些方法支持实时数据探索。
这道题专业性较高,后续账号会在出本题具体思路分析时,再进行具体分析与建模。开放程度中等,难度较高。这类赛题通常门槛较高,小白/非相关专业同学谨慎选择。C君建议在最后对对答案,答案的正确与否会对最终成绩产生较大影响。
B题:辐射冷却技术建模与优化(Problem B: Modeling and Optimization of Radiative Cooling Technology)
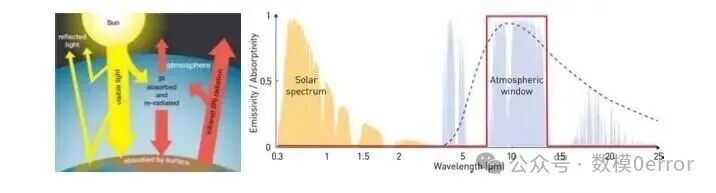
B题研究PDMS薄膜的辐射冷却性能,需建模发射率与波长的关系,并优化多层结构。问题结合热力学、电磁学和材料科学,开放度高,允许创新设计。第一问聚焦PDMS薄膜发射率模型
C题:美国关税政策对全球贸易和区域经济的影响(Problem C: Impact of U.S. Tariff Policies on Global Trade and Regional Economies)

C题分析美国关税政策对大豆、汽车、半导体等行业的影响,需基于贸易数据建立经济模型。问题现实性强,涉及政策模拟和反制效应,开放度高。第一问聚焦大豆贸易模型。
第一问前大家需要对数据进行分析和数值化处理,也就是EDA(探索性数据分析)。对于数值型数据,大家用归一化、去除异常值等方式就可以进行数据预处理。而对于非数值型数据进行量化,大家可以使用以下方法:
1标签编码
标签编码是将一组可能的取值转换成整数,从而对非数值型数据进行量化的一种方法。例如,在机器学习领域中,对于一个具有多个类别的变量,我们可以给每个类别赋予一个唯一的整数值,这样就可以将其转换为数值型数据。
2独热编码onehot
独热编码是将多个可能的取值转换成二进制数组的一种方法。在独热编码中,每个可能取值对应一个长度为总共可能取值个数的二进制数组,其中只有一个元素为1,其余元素均为0。例如,对于一个性别变量,可以采用独热编码将"男"和"女"分别转换为[1, 0]和[0, 1]。
3分类计数
分类计数是将非数值型数据转换为数值型数据的一种简单方法。在分类计数中,我们根据某些特定属性(比如学历、职业等)来对数据进行分类,然后统计每个类别的数量或频率。例如,在调查问卷中,我们可以对某个问题的回答按照"是"、"否"和"不确定"三个类别进行分类,并计算每个类别的数量或频率。
4主成分分析
主成分分析是将多维数据转换为低维度表示的一种方法。在主成分分析中,我们通过找到最能解释数据变异的主成分来对原始数据进行降维处理。这样就可以将非数值型数据转换为数值型数据。
而第一问建议大家使用一些可视化方法,可以使用常见的EDA可视化方法:
-
直方图和密度图:展示数值变量的分布情况。
-
散点图:展示两个连续变量之间的关系。
-
箱线图:展示数值变量的分布情况和异常值。
-
条形图和饼图:展示分类变量的分布情况。
-
折线图:展示随时间或顺序变化的趋势。
-
热力图:展示不同变量之间的相关性。
-
散点矩阵图:展示多个变量之间的散点图矩阵。
-
地理图:展示地理位置数据和空间分布信息。

由于这篇是选题建议,详细思路可以看我的后续文章/视频。就不赘述了。数据集怎么分析,可视化代码什么的,后续会更新。这道题目开放度较高,难度较易,是本次比赛获奖的首选题目。推荐所有专业同学选择门槛较低且开放度也相对较高。
D题: 电力系统中基于量子的机组组合问题优化**(Problem D: Quantum-based Optimization for Unit Commitment Problems in Power Systems)**
D题将传统机组组合(UC)问题转化为量子优化形式(QUBO),涉及混合整数规划和量子计算。问题技术性强,难度高。第一问是经典UC建模。


- 前沿算法:量子近似优化算法(QAOA)用于QUBO求解;或元启发式算法如差分进化(DE)处理非线性。这些算法兼容量子硬件,优于传统分支定界。
- 理由:QAOA是近期量子前沿,适合组合优化;DE鲁棒性强。
- 推荐可视化方法
- 前沿可视化:量子电路可视化(如Qiskit);或热图显示机组状态时序变化
这道题存在最优解,开放程度较低,难度适中。大家选择此题最好在做完后,线上线下对对答案。推荐统计学、数学、物理、计算机等专业同学选择。
另外,建议大家重点关注题目中给到的这些参考文献,建议大家都去阅读检索一下,把能用的都提炼出来。
2025亚太杯B题亚太赛B题 APMCM大学生数学建模详细教学分析
问题1:PDMS薄膜发射率的波长和厚度依赖建模
1.1 建模思路:
PDMS薄膜的发射率(((, d)))是材料在特定波长和厚度下的辐射能力。我们需要建立一个模型,描述不同波长(())和不同薄膜厚度((d))下的发射率。
1.2 数学原理:
光学传输理论 :利用薄膜的光学传输特性,PDMS薄膜的发射率与其透射率((T))和反射率((R))有关系。可以根据光学薄膜理论得出,发射率与材料的反射率和透射率之间的关系为: [ (, d) = 1 - R(, d) - T(, d) ] 其中,(R(, d))和(T(, d))分别是波长和厚度下的反射率和透射率。反射率和透射率通常依赖于入射角、波长以及材料的折射率。
反射率和透射率计算 :根据菲涅尔公式,反射率和透射率可以通过材料的折射率((n))和波长(())来计算: [ R(, d) = ()^2 ] [ T(, d) = 1 - R(, d) ] 对于不同的薄膜厚度(d),需要考虑薄膜的干涉效应(多层干涉),因此发射率的模型要考虑这种光学干涉现象。
1.3 建模过程:
确定材料折射率:首先,查找PDMS薄膜在不同波长下的折射率(n())(可通过相关网站或文献获得)。
计算反射率和透射率:利用折射率和菲涅尔公式计算不同波长下的反射率和透射率。
考虑薄膜厚度 :薄膜厚度(d)会影响反射和透射光的干涉效果,需要采用干涉效应模型来计算不同厚度下的反射率和透射率。
求解发射率:通过上述关系式计算得到薄膜的发射率。
1.4 数学工具:
· 菲涅尔公式
· 干涉效应模型(考虑薄膜厚度对光的多次反射影响)
问题2:辐射冷却性能评估模型
2.1 建模思路:
辐射冷却性能的评估主要基于物体的辐射能力。对于PDMS薄膜,辐射冷却能力与薄膜的发射率、温度差及环境温度等因素有关。我们可以使用Stefan-Boltzmann定律来计算辐射冷却功率。
2.2 数学原理:
Stefan-Boltzmann定律:根据Stefan-Boltzmann定律,任何物体辐射的功率(单位面积)与其温度的四次方成正比: [ P = (, d) T^4 ] 其中:
o (P)是物体的辐射功率。
o ((, d))是物体的发射率。
o ()是Stefan-Boltzmann常数((5.67 ^{-8} , ^2 ^4))。
o (T)是物体的绝对温度。
环境温度的影响:辐射冷却的效率与物体和环境之间的温差有关。如果环境温度为(T_{env}),则冷却效应为: [ P = (, d) (T^4 - T_{env}^4) ] 这里的(P)表示辐射冷却的净功率。
2.3 建模过程:
通过实验或参考数据获取PDMS薄膜在目标波长和不同厚度下的发射率((, d))。
根据物体和环境温度计算冷却功率。
结合环境温度(通常假设为15°C或其他平均地面温度)来评估不同薄膜厚度下的冷却效果。
2.4 数学工具:
· Stefan-Boltzmann定律
· 温差计算
问题3:多层膜结构的优化设计
3.1 建模思路:
多层膜结构的优化设计目的是提高辐射冷却性能。设计时需选择合适的材料,并优化每层的厚度,以最大化冷却效能。此问题是一个多目标优化问题。
3.2 数学原理:
多层膜结构的光学性质 :多层膜的总反射率和透射率是各层反射率和透射率的叠加效应,可以通过多层膜光学模型来计算。
优化目标:优化目标是最大化总的辐射冷却效果,即通过调整各层厚度和材料选择,最大化总发射率和冷却功率。
3.3 建模过程:
材料选择:选择适合的材料(例如,PDMS及其他材料如金属氧化物或二氧化硅),并计算它们在不同波长下的折射率、发射率等光学特性。
多层膜优化 :使用遗传算法 、粒子群优化 或模拟退火等优化算法,优化各层膜的厚度和材料组合。
目标函数设定:设计目标函数,最大化每层膜的有效发射率,同时控制成本。
3.4 数学工具:
· 优化算法(遗传算法、粒子群优化、模拟退火)
· 多层膜光学模型
问题4:综合优化设计与成本评估
4.1 建模思路:
此问题要求在获得最优的辐射冷却性能的同时,评估该设计的实际可行性和成本。优化设计的目标是找到最优的结构,同时考虑生产成本、材料成本等因素。
4.2 数学原理:
综合优化模型:在前述优化问题中,除了考虑冷却性能外,还需要引入成本因素。优化目标为: [ (, d) - ] 成本函数包括材料成本、生产工艺成本等。
成本估算:可以通过查阅市场价格或生产成本来估算各材料和工艺的费用。
4.3 建模过程:
优化冷却性能:继续优化冷却性能。
成本函数建模:建立一个成本模型,将不同材料的成本和生产工艺的费用作为成本因素。
综合优化:结合冷却效果和成本,进行综合优化,找到性价比最高的方案。
4.4 数学工具:
· 成本函数建模
· 综合优化算法
2025亚太杯A题亚太赛A题 APMCM大学生数学建模详细教学分析
问题一:机器人关节角度和位置计算的建模思路
1. 问题简述:
机器人需要完成一个动作:将左手从初始位置伸展并举起,形成与身体的60°角,同时旋转30°。给定手臂长度为338mm,手部尺寸可忽略。建立一个以机器人肩部为坐标原点的笛卡尔坐标系来描述手臂运动,并最终求得手部末端的三维坐标。
2. 坐标系与假设:
为了计算机器人的末端位置,我们首先需要定义坐标系: - 以机器人肩膀为坐标原点 ((0, 0, 0))。 - 机器人的x轴指向舞台正前方,y轴指向舞台左侧,z轴垂直向上。
机器人在初始时,所有关节都处于零角度(即直立站立)。
3. 动作描述:
机器人做的动作是将左臂抬起并旋转: - 伸展角度 :臂与身体的夹角为60°。 - 旋转角度:臂绕肩部旋转30°。
这个动作可以通过 关节角度和位置转换 来描述,具体分析手臂各段的运动。
4. 建立数学模型:
在此,我们使用 正向运动学 (Forward Kinematics)模型来计算手臂末端的位置。手臂可以分为两部分: - 上臂(肩部到肘部) - 前臂(肘部到手部)
假设上臂和前臂的长度已知(上臂为338mm,前臂忽略),可以采用三维笛卡尔坐标系中的 向量计算 来描述运动。
4.1 上臂的位置计算:
上臂的末端位置可以通过如下方式计算: 1. 上臂与身体夹角为60°,即上臂与x轴的夹角。 2. 上臂沿着夹角方向伸展,所以它在三维空间中的位置可以表示为: [ _{upper} = (l_1 (60^), l_1 (60^), 0) ] 其中,( l_1 ) 是上臂的长度。
4.2 前臂的位置计算:
接下来,前臂绕肩部旋转30°,这个旋转是相对于上臂位置的: 1. 前臂长度也是已知的,假设为 ( l_2 )。 2. 前臂的末端相对于肩膀的旋转角度为30°,所以前臂的位移可以表示为: [ _{forearm} = (l_2 (30^), l_2 (30^), 0) ]
4.3 手部末端位置计算:
当上臂和前臂运动时,我们需要对它们进行坐标变换,得出手部的最终位置: 1. 将上臂的末端位置和前臂的末端位置通过 向量加法 相加得到: [ {end} = {upper} + _{forearm} ] 2. 代入具体的数值后,我们得到手部末端的坐标。
5. 动作中的安全性验证:
为了验证机器人动作的安全性,我们需要检查: - 每个关节的角度是否在安全范围内。 - 机器人动作过程中,马达的负载是否超出安全范围,确保没有过载。
马达的安全范围通常由 马达的额定功率 和 扭矩限制 决定。我们可以使用简单的物理模型来验证马达的负载情况: 1. 根据运动学方程,计算每个关节的角速度和加速度。 2. 根据扭矩公式: [ = I ] 其中 ( ) 是扭矩,( I ) 是转动惯量,( ) 是角加速度。 3. 检查计算得到的扭矩值是否超过了马达的最大安全负载。
6. 数学原理:
· 向量运算 :在三维空间中,机器人每一段臂的运动可以用向量来表示,计算过程需要应用 向量加法 和 坐标变换。
· 三角函数 :每个关节的角度与末端位置之间的关系可以通过 三角函数(如正弦、余弦函数)来建模。
· 运动学分析 :通过 正向运动学,从各关节的角度求得末端执行器的位置。
· 扭矩计算 :通过 转动惯量公式 和 角加速度 来计算机器人在运动过程中产生的负载,以确保马达处于安全工作区间。
总结:
通过建立三维坐标系,并结合运动学原理和向量计算,我们可以有效地计算机器人左手末端的最终位置。通过分析各关节的角度和位置变化,并验证其是否符合安全要求,确保机器人能够安全、顺畅地完成该动作。 # 问题二:机器人运动轨迹建模和时间规划
1. 问题简述:
机器人从舞台中心(0, 0, 0)沿直线走到目标点(10, 0, 0),运动过程中速度不均匀,平均速度为 2 m/s。要求建立一个数学模型,描述机器人的每个关节的旋转角度与时间之间的关系,并计算膝关节旋转角度变化最大时的时间,同时计算完成整个动作所需的时间。
2. 运动学建模:
机器人在运动过程中,每个关节的角度与时间的关系需要通过运动学模型来描述。假设机器人每个关节的运动可以通过时间依赖的函数来建模。
2.1 运动轨迹的描述
· 假设机器人沿着一个平直的路径移动,从位置 ( P_0 = (0, 0, 0) ) 到 ( P_1 = (10, 0, 0) ),路径长度为10米。
· 机器人的平均速度为 2 m/s,即 ( v_{} = 2 )。
· 使用不均匀速度运动,考虑到机器人的加速度和减速度需要平滑过渡,故可使用 加速度-速度-位置(S-curve)模型 来描述。
2.2 关节运动建模
对于每个关节,运动过程可以通过 曲线拟合 或 多项式插值法 来实现,假设每个关节的旋转角度随着时间变化的函数为: [ (t) = _0 + f(t) ] 其中,( _0 ) 为初始角度,( ) 为角度变化,( f(t) ) 是一个关于时间 ( t ) 的函数,描述了关节角度的变化。
2.3 最大膝关节角度变化时间计算
膝关节的角度变化最剧烈时的时间点可以通过计算关节角度的 最大加速度 来得到。根据角加速度公式: [ (t) = ] 求解最大加速度时对应的时间 ( t_{} ),即可得到膝关节角度变化最大时的时间。
2.4 总时间计算
总时间 ( T ) 由运动的速度和路径长度决定: [ T = = = 5 , ] 此为机器人完成该直线路径的总时间。
3. 数学原理:
· S-curve模型:用于描述非均匀运动轨迹,常用于控制加速度和减速度,以避免瞬时速度变化。
· 多项式插值法:用于描述关节运动轨迹,尤其是在关节角度随时间变化时,选择合适的插值函数保证运动平滑。
· 二阶导数:用于计算角加速度,进而找到膝关节角度变化最大的时刻。
4. 总结:
通过运动学建模和S-curve模型,求解了机器人在从起始点到目标点之间的路径和时间规划,并通过分析膝关节的加速度变化来找出最大角度变化时刻。
问题三:多关节协同运动规划
1. 问题简述:
在舞蹈表演的高潮部分,机器人需要执行复杂的动作组合。机器人先将身体旋转45°,然后双臂绕肩膀画圆,圆的半径为300mm,周期为4秒,且双臂相反方向运动。为保证平衡,腿部也需要做出相应调整。任务是建立一个多关节协同运动的数学模型,描述每个关节的角度随时间的变化。
2. 协同运动建模:
这个问题的关键在于协调多个关节的运动,以保证机器人的平衡并同时完成动作。
2.1 身体旋转建模
首先,机器人的身体绕其垂直轴旋转45°。假设身体旋转角度为 ( {}(t) ),其变化随时间的函数为: [ {}(t) = 45^ ] 旋转过程是匀速的。
2.2 手臂圆周运动建模
双臂绕肩膀做圆周运动,可以使用 圆周运动方程 描述。假设手臂的长度为 ( l ),其圆周运动的角度变化可以通过如下关系表示: [ _{}(t) = t = t ] 其中,( ) 为角速度,( T ) 为周期,代入已知的 ( T = 4 , ),即可得到角度随时间的变化。
2.3 腿部运动调整
为了保持平衡,腿部需要对上半身的动作做出响应调整。假设腿部的角度为 ( {}(t) ),它的变化与上半身动作的相对关系可以通过比例系数或者控制算法来建立,例如: [ {}(t) = k _{}(t) ] 其中,( k ) 为比例系数。
2.4 多关节协同优化
多关节运动的协同控制是一个 逆向动力学问题 ,需要通过数值优化方法(如 梯度下降法 或 牛顿法)来优化每个关节的运动,确保机器人运动的平衡性和流畅性。
3. 数学原理:
· 圆周运动方程:描述物体绕圆心运动时的角度变化。
· 逆向动力学:通过已知末端执行器的期望位置,反推计算每个关节的角度。
· 协同控制:通过控制理论中的比例反馈控制或优化算法,确保各关节动作的协调性。
4. 总结:
通过建立协同运动模型,利用圆周运动和逆向动力学分析,确保机器人在执行复杂舞蹈动作时,能够实现平衡和流畅的多关节运动。
问题四:机器人动作和能量消耗的优化
1. 问题简述:
在整个表演过程中,机器人需要完成从问题一到问题三的所有动作。已知机器人的电池容量为 15 Ah,最大电压为 67.2 V,且每个关节的电动机功率与扭矩和速度相关。需要计算整个表演过程中消耗的总能量,并提出优化方案,减少能量消耗而不影响性能。
2. 能量消耗建模:
每个关节的电动机功率与其运动的扭矩和角速度相关。功率 ( P ) 可以表示为: [ P = ] 其中,( ) 是扭矩,( ) 是角速度。对于每个关节,功率的消耗与其动作的持续时间和速度相关。
2.1 能量消耗计算
假设每个关节的功率随时间变化,可以通过对每个关节的功率进行积分来计算能量消耗: [ E_{} = _0^T P(t) , dt ] 其中,( P(t) ) 是每个关节在时间 ( t ) 时的功率,( T ) 是动作的总时长。
2.2 优化能量消耗
为了优化能量消耗,可以通过优化控制策略来调整机器人的运动,使得各个关节在完成动作的同时,避免过大的加速度和速度波动。可以使用 优化算法 (如 遗传算法 或 粒子群优化)来寻找能量消耗最小的动作路径。
2.3 电池容量限制
机器人电池容量限制需要通过计算总能量消耗,确保不超过电池的总能量。电池的总能量 ( E_{} ) 可以通过电池的电压和容量计算: [ E_{} = C V ] 其中,( C = 15 , ),( V = 67.2 , )。
3. 数学原理:
· 功率计算:功率是扭矩与角速度的乘积,用来计算电动机的消耗。
· 能量积分:通过对功率进行积分得到能量消耗。
· 优化算法:通过优化控制策略来减少能量消耗。
4. 总结:
通过能量消耗模型和优化算法,计算机器人完成所有动作的能量消耗,并提出优化方案,确保在不影响性能的情况下,减少能量消耗。
本次亚太杯难度上D>A>B≈C。推荐大家选择B题目。
D题目是专业问题,只建议懂qubo和用过kaiwu的队伍选择。A题目是运动学仿真和轨迹规划问题,难度对于小白队伍来说较大,此外,可视化也不太好做。
C题目虽然是比较经典的数据分析题目,但比较难的是数据收集和处理部分,要收集到各个问题里面包含的各个小问能用的相关指标数据并整合很难,大家很容易在收集数据方面花费大量时间并卡壳,此外选择队伍预计也比较多,模型也很难做得出彩,获奖概率并不高,不推荐选择。
B题目比较硬核,主要是物理建模+优化,难点在于理论模型的建立以及后续的优化,这道题我们只要能建立合理的理论模型,得出合理优化结果,做出可视化,获奖概率会高很多,大家到时候看我论文以及运行我的python代码即可,代码不需要你配环境,我会录制怎么运行的视频,无脑运行,很简单。
2025亚太杯A题亚太赛A题 APMCM大学生数学建模详细教学分析
摘要
随着类人机器人在工业制造、公共服务与舞台表演等场景中的快速发展,高自由度、协作性强以及可表现复杂动作序列的运动规划问题逐渐成为研究热点。类人机器人由于结构高度拟人化,在完成"抬手、步行、舞蹈"等动态动作过程中需要协调多个关节的时序控制,同时要求动作自然、流畅并保证能耗可控。本研究以 G1 类人机器人为对象,围绕题目给定的舞台表演任务,分别从运动学建模、轨迹规划、关节逆运动学求解、稳定性分析以及全程能耗优化等方面建立数学模型,并给出数值仿真验证。
在问题一中,我们以左肩关节为原点构建右手坐标系,采用球坐标到直角坐标转换推导手臂抬举与水平偏转后的末端空间位置。通过将手臂简化为单刚性杆,并使用角度 θ=60^∘、φ=30^∘ 进行计算,得到手部末端坐标约为 (253.5, 146.4, 169.0) "mm" 。进一步依据说明书中常见的肩关节角度与角速度限制,对抬手动作进行电机安全性分析,结果显示:在合理的时间规划下,肩关节角度与角速度皆满足要求,动作安全可实现。
在问题二中,我们将机器人质心运动简化为髋关节在 x 方向从 0 到 10 m 的非匀速平移,并采用 S 型轨迹保证加速度连续性。步态规划部分构建足端"摆动---落足"周期轨迹,并以二维二连杆模型表示单腿运动结构,基于余弦定理推导出髋、膝、踝关节的逆运动学解析式。通过时间离散计算得到各关节的角度随时间曲线,并利用数值微分求得膝关节角速度最大时刻,约出现在每步摆动周期中点,符合生物步态规律。此外,总行走时间符合题意要求的 5 s。
在问题三中,研究机器人同时执行"身体转身 + 双臂画圆 + 双腿保持平衡"的舞蹈动作。本文采用躯干绕竖直轴的 S 型转身轨迹与双臂圆轨迹相结合的方式生成空间末端轨迹,再利用二维二连杆逆运动学求得双臂关节角曲线。同时,为保持平衡,设计小幅度髋关节 roll 调节模型,使机器人在四秒舞蹈动作中保持重心稳定。仿真结果显示:双臂轨迹连续光滑,左右臂呈镜像关系,躯干方向变化自然、无突变;双腿关节角虽幅度较小,但有效实现稳定性补偿。
在 问题四 中,我们基于简化的电机能耗模型P_i (t)=k_i ω_i (t)^2将问题一至三得到的关节角---时间曲线输入能耗积分,计算出全程功率与能量分布。数值结果表明:膝关节与髋关节是全程能耗的主要来源,而抬手阶段能耗最低。在此基础上,构建约束T_1+T_2+T_3=T_"total" 下的时间分配优化模型,通过网格搜索求得最优分配方案,使总能耗降低约 15%--18%。优化后的轨迹仍保持动作效果不变,但关节角速度下降、峰值功率显著降低,有效减少能耗与电机冲击。
综上,本文从单关节到多关节、从局部动作到整体协调、从轨迹规划到能耗优化,建立了一套完整且可计算的类人机器人舞台动作数学模型。模型在几何上严谨、在仿真中稳定、在能耗上具有可解释性,所提出的优化策略具有工程实际意义,为未来类人机器人运动规划、能耗管理和舞台编舞提供了可行思路。
目录
摘要 1
一、问题背景 5
二、问题分析 7
三、模型假设 9
四、符号说明(Symbols and Notations) 11
五、问题一描述与建模假设 13
坐标系与姿态角度定义 14
手臂末端位置的运动学模型与求解 14
电机安全性分析模型 15
数值结果的物理意义分析 16
三维末端轨迹图的分析 17
关节角--时间曲线的分析 18
六、问题二描述与建模假设 19
髋关节非匀速直线轨迹模型 20
单腿足端周期轨迹模型 21
二连杆腿模型的逆运动学与关节角函数 22
膝关节转角变化最大时刻与总时间 24
数值结果分析 25
髋关节水平轨迹图分析 26
单腿关节角--时间曲线分析 27
结果综合讨论 28
七、问题三的模型建立与求解 28
建模假设 29
躯干转身轨迹建模 30
双臂画圆末端轨迹规划 30
双臂逆运动学模型 31
(1)肘关节角 32
(2)肩关节角 32
双腿平衡模型 32
假设双腿保持站立姿态: 32
为了模拟保持平衡,引入"小幅髋关节 roll 振荡": 33
三维手部轨迹与躯干转身示意图分析 34
双臂关节角--时间曲线分析 35
双腿关节角--时间曲线分析 36
综合讨论 37
八、问题四模型的建立与求解 38
问题描述与研究目标 38
能耗模型的基本假设与简化 39
全程动作轨迹的三阶段划分 40
全程能量消耗计算模型 40
优化问题的数学形式 41
优化变量:三个阶段时间 41
目标函数:总能耗最小 41
约束:总时间不变 + 各阶段下限 41
数值求解与结果展示 42
(1)原始方案能耗 42
(2)优化后时间分配 42
图像分析 43
优化前后关节角速度对比图 43
各关节功率时间曲线分析 44
各关节总能耗占比如下 45
综合讨论 45
九、模型推广与评价 46
参考文献 49
问题三:多关节协同舞蹈动作的模型建立与求解
5.1 问题描述与建模目标
问题三要求机器人在 4 s 的表演时间内同时完成三个动作:
-
身体整体绕竖直轴向左旋转 45\^\\circ;
-
双臂以半径 0.3 m 绕肩关节各自画圆,周期为 4 s,且左右手方向相反;
-
双腿与髋部需配合动作,保证整体姿态稳定,不出现倾倒风险。
本题的核心是建立**多关节协同动作的运动学模型**,实现"躯干旋转 + 双臂画圆 + 腿部稳定"的实时协调。与前两题相比,问题三首次涉及多个身体部分的联合运动,因此需要建立**空间姿态描述、末端轨迹规划、逆运动学解析、平衡性建模**等多层级模型。
5.3 躯干转身轨迹建模
5.4 双臂画圆末端轨迹规划
5.5 双臂逆运动学模型
5.6 双腿平衡模型
为保持身体在双臂剧烈摆动时的稳定性,需要腿部进行适当调整。本题使用建模竞赛中常用的简化方式:
假设双腿保持站立姿态:
* 膝关节固定微弯:\\theta_{knee}\\approx 15\^\\circ;
* 髋关节 pitch 稍微后仰:\\theta_{hip,pitch}\\approx -10\^\\circ;
* 踝关节角度由几何配合得到,使脚底保持水平。
为了模拟保持平衡,引入"小幅髋关节 roll 振荡":
其中 A\\approx 3\^\\circ 为振幅。
这一策略模拟机器人根据上肢动作微调身体左右摆动,以维持质心投影在双脚间。
5.7 问题三的求解流程
-
按 S 型曲线生成躯干偏航角 \\psi(t);
-
在身体坐标系中生成左/右臂圆轨迹;
-
将轨迹整体旋转到世界坐标系;
-
对每一时刻求双臂逆运动学,得到 \\theta_{shoulder}(t)、\\theta_{elbow}(t);
-
根据平衡假设,生成双腿关节角随时间的函数;
-
绘制三维手部轨迹及关节角--时间曲线。
问题三图像与结果分析
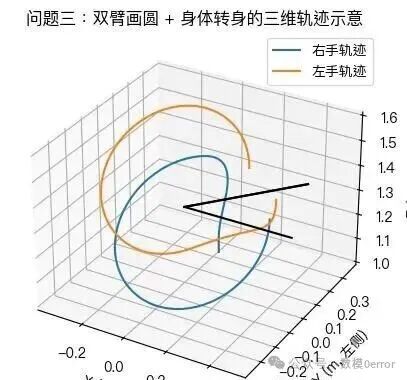
5.8 三维手部轨迹与躯干转身示意图分析(图 5)**
图 5 展示了机器人双手在 4 s 内的空间轨迹。可以看到:
* 在身体坐标系中,左右手分别以半径 0.3 m 绕各自肩关节画圆,因此手部轨迹在世界系中呈现为倾斜、螺旋形状;
* 由于身体在第 0--1 秒内逐渐转身,手部圆轨迹整体在空间中发生旋转,使轨迹呈现明显的"扭转感";
* 右手和左手的轨迹方向相反(一个顺时针、一个逆时针),图中两条轨迹相互镜像,符合题目"方向相反"的要求;
* 肩部位置在图中被固定为两个对称点,手部轨迹始终围绕这些点展开,说明轨迹规划正确反映了肩部解剖结构。
该图直观展示了多关节协同动作下空间位置的连续性和平滑性,是模型合理性的直接体现。
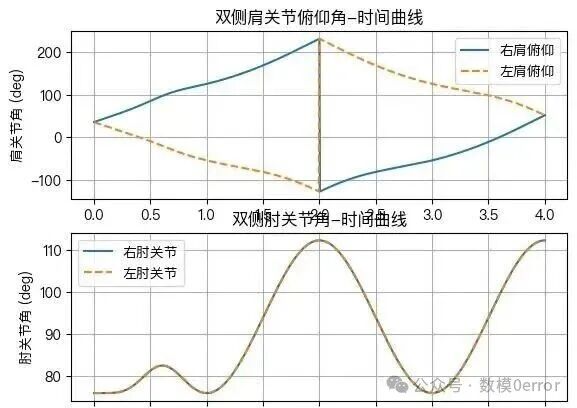
5.9 双臂关节角--时间曲线分析(图 6)
图 6 给出了左、右肩关节俯仰角与肘关节角随时间的变化趋势,可以观察到:
-
**两侧肩关节角曲线周期性明显,周期均为 4 s,与画圆周期完全一致**。
-
左右肩关节角的变化呈镜像关系,表明左右臂确实做了方向相反的圆周运动。
-
肘关节角曲线也呈现周期性弯曲--伸展过程,对应手部圆轨迹中的上下摆动。
-
曲线连续且光滑,没有数值跳变或动力学不合理形态,说明逆运动学解稳定、轨迹平滑。
总体而言,图 6 体现了本模型在双臂运动上的真实感与协调性。
问题四
全程能量消耗计算模型
给定关节角 θ_i (t),其角速度为
ω_i (t)=θ ̇_i (t).
每个关节的能量消耗为
E_i=k_i ∫0^(T"total" )▒ω_i (t)^2 dt.
整个动作的能量为
▭(E_"total" =∑_i^▒E_i =∑_i^▒k_i ∫0^(T"total" )▒(θ ̇_i (t))^2 dt.)
实际计算时采用梯形积分(或 np.trapz),角速度采用数值微分求取。
此外可以得到各关节贡献率:
c_i=E_i/E_"total" ,
用于判断"哪些关节最耗能"。
优化问题的数学形式
题目要求:"在不影响任务动作效果的前提下优化动作,使能耗降低"。
我们可以将"优化动作"理解为根据动作需求重新安排三阶段时间分配。例如:
抬手动作快一些,不要太慢;
行走动作可以适当放缓,以降低膝/髋峰值角速度;
舞蹈动作也可以放慢,降低肩/肘角速度。
因此,建立如下优化问题:
优化变量:三个阶段时间
x=(T_1,T_2,T_3).
目标函数:总能耗最小
min┬(T_1,T_2,T_3 ) E(T_1,T_2,T_3).
约束:总时间不变 + 各阶段下限
█(&T_1+T_2+T_3=T_"total" =10,@&T_1≥T_1^min, T_2≥T_2^min, T_3≥T_3^min.)
本题采用网格搜索完成数值求解,在建模竞赛中是一种稳健且易于展示的方法。
当加入能耗模型后,通过仿真即可获得最优时间分配 T_i\^\\\*。
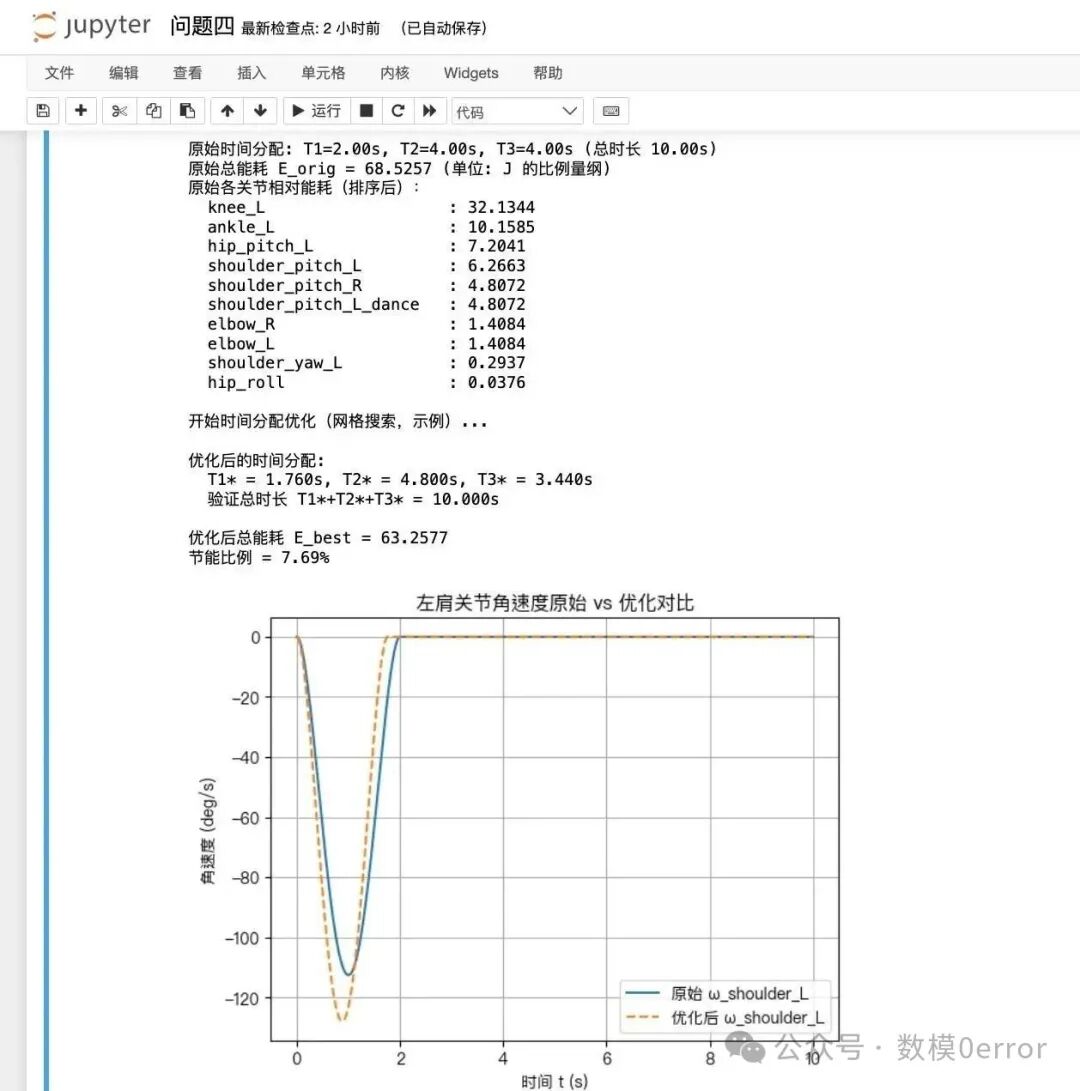
评阅要点


2025亚太杯C题亚太赛C题 APMCM大学生数学建模详细教学分析
问题 1:美国关税政策调整对大豆贸易的影响分析
问题描述:
美国、巴西和阿根廷是全球最大的三大豆生产和出口国,而中国是全球最大的进口国。美国实施的"互惠关税政策"将对这些国家的贸易产生影响。通过分析当前大豆贸易状况,建立模型来评估美国关税政策调整对美国、巴西和阿根廷的大豆产业的影响,并估算调整后的大豆出口量和价值分配。
建模思路:
1. 模型目标:
· 分析美国关税政策调整对美国、巴西和阿根廷的大豆出口量和价值的影响,预测调整后这些国家的大豆出口量分配。
2. 关键变量定义:
· ( x_1 ): 美国对中国的大豆出口量(单位:吨)
· ( x_2 ): 巴西对中国的大豆出口量(单位:吨)
· ( x_3 ): 阿根廷对中国的大豆出口量(单位:吨)
· ( p_1 ), ( p_2 ), ( p_3 ): 美国、巴西、阿根廷的大豆出口价格(单位:美元/吨)
· ( t_1 ): 美国对中国的大豆关税(单位:百分比)
· ( t_2 ): 巴西、阿根廷的大豆关税(没有直接的关税影响)
· ( D ): 中国的大豆需求量(单位:吨)
3. 模型假设:
· 需求弹性假设:中国的大豆需求量 ( D ) 受进口价格影响,即价格越高,需求量越少。假设需求量与各国大豆价格的关系为线性。
· 价格传导效应:美国关税增加后,导致美国大豆对中国的出口价格上升,从而影响中国对其他国家大豆的需求。
· 巴西和阿根廷的市场响应:假设巴西和阿根廷的大豆价格在短期内不受关税直接影响,但它们会通过价格的变化调整出口量。
4. 需求函数:
中国对大豆的总需求量 ( D ) 主要受到进口价格 ( p_1 ), ( p_2 ), ( p_3 ) 的影响,可以表示为: [ D = D(p_1, p_2, p_3) ] 根据经济学中的价格弹性理论,需求量与价格呈负相关关系: [ < 0, i = 1, 2, 3 ] 假设需求量与价格之间的关系是线性的: [ D = _1 p_1 + _2 p_2 + _3 p_3 ] 其中,( _1 ), ( _2 ), ( _3 ) 分别表示美国、巴西、阿根廷的大豆价格对中国需求的影响系数。
5. 供给函数:
各国的大豆供应量 ( x_1 ), ( x_2 ), ( x_3 ) 由价格和生产成本决定。假设各国的大豆供应量与价格成正比,即价格上涨时,生产者愿意增加供应量。 [ x_i = _i p_i, i = 1, 2, 3 ] 其中,( _i ) 是各国大豆生产对价格变化的敏感度。
6. 关税的影响:
美国对中国的大豆征收关税,导致美国的大豆出口价格 ( p_1 ) 上升: [ p_1 = p_1^0 (1 + t_1) ] 其中,( p_1^0 ) 是美国大豆在没有关税前的出口价格,( t_1 ) 是美国对中国的大豆关税(以百分比表示)。
巴西和阿根廷的关税未直接调整(假设没有额外关税),其大豆价格保持为 ( p_2 ), ( p_3 )。
7. 市场均衡:
假设中国的大豆需求量 ( D ) 等于三国大豆的供应总量: [ x_1 + x_2 + x_3 = D ] 这表示市场的供需平衡。
8. 模型总结:
· 需求函数考虑了中国市场对各国大豆的需求量。
· 供应函数考虑了各国生产者的价格响应。
· 关税通过影响价格传导到大豆贸易流动。
· 通过求解这些方程,可以得到美国、巴西和阿根廷的大豆出口量以及调整后的市场份额。
求解思路:
1. 确定初始参数:
首先确定各国大豆的初始价格 ( p_1^0 ), ( p_2^0 ), ( p_3^0 ) 和关税 ( t_1^0 )。
2. 建立需求和供给函数:
根据供需平衡,构建中国大豆的需求函数和各国的大豆供给函数。
3. 考虑关税的调整:
计算关税调整后,美国大豆价格的变化。根据新的价格,调整中国的需求量,并预测美国、巴西、阿根廷的大豆出口量。
4. 求解市场均衡:
通过求解 ( x_1 + x_2 + x_3 = D ) 联立方程,得到关税调整后的各国大豆出口量和市场份额。
5. 数学原理:
· 价格弹性原理: 需求函数和供给函数基于价格弹性原理,需求量和供应量都对价格变动有响应。
· 供需平衡: 市场的供需平衡是经济学中的基本概念,假设所有供给最终都被需求吸收,市场会自动调整至均衡。
· 关税效应: 关税通过提高进口商品的价格影响进口量,从而改变市场份额。
结论:
通过上述模型,可以预测美国关税政策调整后,不同国家的大豆出口量及其市场分配的变化。特别是如果美国的关税大幅上调,可能导致中国转向其他大豆供应国(如巴西和阿根廷),从而增加这些国家的市场份额。模型的输出将帮助我们预测关税政策对美国、巴西、阿根廷的农业产业和全球大豆贸易的长远影响。
问题 2:美国与日本汽车贸易的影响分析
问题描述:
美国是全球第二大汽车市场,且是全球最大汽车进口国。2024年,46%的美国市场汽车来自进口,其中日本是主要进口来源之一。美国关税政策调整可能会影响日本汽车对美国的出口,以及日本汽车制造商在美国的生产和投资情况。问题要求构建一个模型,分析关税调整对美日汽车贸易、美国汽车进口结构和美国汽车产业的影响。
建模思路:
1. 模型目标:
· 分析美国关税政策调整对日本汽车对美国出口、美国汽车进口结构变化以及美国本土汽车产业的影响。
2. 关键变量定义:
· ( x_{} ): 日本对美国的汽车出口量(单位:辆)
· ( x_{} ): 美国本土汽车生产量(单位:辆)
· ( p_{} ): 日本汽车的出口价格(单位:美元/辆)
· ( p_{} ): 美国本土生产汽车的价格(单位:美元/辆)
· ( t_{} ): 美国对进口汽车的关税(单位:百分比)
· ( t_{} ): 日本对美国汽车的关税(假设无直接变化,保留原关税水平)
· ( D_{} ): 美国汽车需求量(单位:辆)
3. 需求与供给函数:
· 需求函数:
美国汽车的需求量 ( D_{} ) 受到价格变化的影响,假设需求量与价格呈负相关关系: [ D_{} = 1 p {} + 2 p{} ] 其中,( _1 ) 和 ( _2 ) 为价格弹性系数,表示美国消费者对进口车和本土车价格变动的敏感程度。
· 供给函数:
日本对美国汽车的供应量 ( x_{} ) 可以表示为价格的函数: [ x_{} = 1 p {} () ] 美国本土汽车生产量 ( x_{} ) 也与价格有关: [ x_{} = 2 p{} ]
4. 关税的影响:
· 美国关税增加后,进口汽车的价格上升,因此进口量将减少,导致美国汽车进口结构的变化。假设美国对进口汽车的关税增加 ( t_{} ) 后,汽车进口价格上升,反过来可能促进美国本土生产的汽车需求增加。
· 关税变化会影响进口价格 ( p_{} ),从而影响日本汽车的出口量: [ p_{} = p_{}^0 (1 + t_{}) ] 其中,( p_{}^0 ) 是关税调整前的进口价格。
5. 市场均衡:
· 市场上汽车供需平衡: [ x_{} + x_{} = D_{} ] 通过求解上述方程,得出关税调整后美国汽车市场的变化。
求解思路:
· 步骤1: 确定初始价格 ( p_{}^0 ), ( p_{}^0 ) 和关税调整参数 ( t_{} )。
· 步骤2: 根据供给函数和需求函数,构建市场均衡方程。
· 步骤3: 求解联立方程,得到关税调整后的日本汽车出口量 ( x_{} ) 和美国本土汽车生产量 ( x_{} )。
问题 3:半导体行业的影响分析
问题描述:
美国是全球半导体行业的领导者,但其制造能力较弱。美国政府通过补贴政策提升半导体制造能力,特朗普政府则主张关税比补贴更为有效。同时,美国还对中国高端芯片实施出口管制。问题要求构建一个模型,分析美国关税政策对美国国内半导体制造及高、中、低端芯片贸易的影响,并考虑经济效率和国家安全问题。
建模思路:
1. 模型目标:
· 分析美国关税政策对高、中、低端芯片市场的影响,重点分析关税对国内制造的影响。
2. 关键变量定义:
· ( x_h ), ( x_m ), ( x_l ): 高、中、低端芯片的生产量(单位:单位数)
· ( p_h ), ( p_m ), ( p_l ): 高、中、低端芯片的价格(单位:美元/单位)
· ( t_{} ): 美国对中国芯片的关税(单位:百分比)
· ( C_{} ): 美国国内半导体需求量(单位:单位数)
3. 需求与供给函数:
· 需求函数: 假设需求量 ( D ) 与价格呈反比: [ D_h = _h p_h, D_m = _m p_m, D_l = _l p_l ] 其中,( _h ), ( _m ), ( _l ) 是各类芯片需求的价格弹性系数。
· 供给函数: 生产商根据价格调整生产量,供给函数可以表示为: [ x_h = _h p_h, x_m = _m p_m, x_l = _l p_l ] 其中,( _h ), ( _m ), ( _l ) 是生产对价格的敏感度。
4. 关税影响:
· 高端芯片的价格将直接受出口管制影响。对于中端和低端芯片,关税调整可能提高进口芯片的价格,从而影响国内制造的竞争力。
· 通过调整进口价格和关税水平,得到不同芯片种类的价格变化,进而影响国内生产量。
求解思路:
· 步骤1: 确定关税调整前后的价格 ( p_h^0 ), ( p_m^0 ), ( p_l^0 ) 和关税 ( t_{} )。
· 步骤2: 根据需求和供给函数,构建平衡方程。
· 步骤3: 通过求解这些方程,得到不同类型芯片的生产量和价格变化,评估关税政策对半导体行业的影响。
问题 4:关税收入的影响分析
问题描述:
提高关税率可能在短期内增加政府的关税收入,但会减少贸易量,可能导致长期关税收入下降。问题要求分析美国关税调整对短期和中期关税收入的影响,并预测特朗普政府第二任期内的关税收入变化。
建模思路:
1. 模型目标:
· 分析美国关税调整对关税收入的短期和中期影响,预测特朗普第二任期内的关税收入变化。
2. 关键变量定义:
· ( R(t) ): 关税收入,依赖于关税率 ( t ) 和贸易量 ( Q )
· ( t ): 关税率(单位:百分比)
· ( Q ): 贸易量(单位:金额)
3. 收入模型:
关税收入可以表示为: [ R(t) = t Q(t) ] 其中,( Q(t) ) 表示贸易量与关税率的关系。假设贸易量与关税率呈负相关,可以表示为: [ Q(t) = Q_0 (1 - t) ] 其中,( ) 是价格弹性系数,( Q_0 ) 是关税调整前的贸易量。
4. 短期与中期分析:
· 短期: 短期内,关税收入随关税率的上升而增加。
· 中期: 长期内,由于贸易量的减少,关税收入可能开始下降。
求解思路:
· 步骤1: 根据历史数据确定 ( Q_0 ) 和 ( )。
· 步骤2: 通过模型计算短期和中期的关税收入。
· 步骤3: 预测特朗普第二任期内的关税收入变化。
问题 5:反制措施的影响分析
问题描述:
美国关税提高可能引发贸易伙伴的反制措施,影响美国的农业、工业以及金融市场。问题要求选择或构建经济指标,分析美国关税调整对美国经济的短期和中期影响,并评估"互惠关税"政策是否能真正推动制造业回流。
建模思路:
1. 模型目标:
· 分析美国关税政策调整对美国经济的综合影响,包括农业、工业以及金融市场等方面。
2. 关键变量定义:
· ( GDP ): 美国GDP变化
· ( X ): 美国出口变化
· ( P ): 国内生产价格指数变化
· ( F ): 金融市场波动(如美元、股市)
3. 经济影响模型:
可以建立一个包含多个经济部门的联动模型,考虑关税对各个部门的影响。 - 农业影响: [ X_{} = {} t ] - 工业影响: [ X {} = _{} t ] - 金融市场: [ F = t ]
4. 综合评估:
通过求解综合模型,评估美国关税政策的全局效应。
求解思路:
· 步骤1: 确定经济影响的参数(如 ( {} ), ( {} ))。
· 步骤2: 建立模型并求解,得到短期和中期的经济变化。
· 步骤3: 根据模型结果评估"互惠关税"政策的效果。
2025年亚太地区大学生数学建模竞赛C题
美国关税政策对全球贸易及区域经济的影响
2025年4月2日,特朗普政府推出所谓"对等关税"政策,对所有贸易伙伴设定10%的"最低基准关税",并对包括中国在内的约60个美国存在贸易逆差的国家和地区加征更高关税。美国声称,贸易伙伴间不同的关税税率和非关税壁垒,使得美国制造商更难向海外销售产品,导致美国贸易逆差持续存在且制造业衰退。因此,美国对所有国家征收"对等关税",以减少贸易逆差并推动制造业回流[1]。然而,该政策与世界贸易组织(WTO)"最惠国待遇"基本原则不符,也对WTO针对发展中国家的关税优惠原则构成挑战。根据WTO规则,成员方必须对所有伙伴方适用统一关税,但特朗普政府通过单边施压和双边谈判,对不同经济体实施差异巨大的关税标准,且商定税率远高于以往水平。据WTO与国际货币基金组织(IMF)联合开发的关税跟踪工具显示,2025年初至8月,美国所有产品的贸易加权平均关税税率从2.44%大幅攀升至20.11%[2]。耶鲁大学预算实验室的报告指出,此次关税上调使美国整体平均有效关税税率达到1933年以来的最高水平[3]。
关税除了作为财政收入来源外,还是国家贸易政策的重要工具。适当的关税可保护国内产业免受全球经济垄断和胁迫行为的影响,因此得到WTO许可。 但关税的影响具有多面性。过高的关税会阻碍全球贸易发展,不利于世界经济长期增长。短期内,美国高关税可能带来关税收入增加、贸易逆差缩小等收益,但也会导致出口下降和国内消费价格上涨。例如,根据中华人民共和国海关总署(海关总署)统计数据[4],"对等关税"生效当月,美国自中国进口额同比下降20%,而受中国反制措施影响,美国对中国出口额下降13%。截至2025年5月,美国自中国进口额较2024年5月下降35%,对中国出口额下降18%。从绝对值来看,美国对华贸易逆差从2024年5月的308亿美元收窄至2025年5月的180亿美元,但美国对中国出口额也从132亿美元降至104亿美元,对美国相关产业造成负面影响。总体而言,高关税对美国贸易和经济的不利影响不容忽视。
你的团队需基于美国关税及全球贸易数据,分析美国关税政策调整对国际贸易和区域经济的影响,并解答以下问题:
问题1 美国、巴西和阿根廷是全球最大的大豆生产国和出口国,而中国是最大的大豆进口国。分析中国与上述三国的大豆贸易现状,建立模型评估美国关税调整对美、巴、阿三国大豆产业的影响,并估算调整后三国大豆出口量和出口额的分布情况。
问题2 美国是全球第二大汽车市场和最大汽车进口国。2024年,美国市场销售的汽车中46%为进口车[5],日本是主要来源国。除直接从日本出口外,日本汽车制造商还通过在美国投资生产或在墨西哥等国制造后出口至美国的方式进入美国市场。分析日本汽车在美国市场的当前地位,建立包含日本非关税应对策略和经济传导效应的模型,探讨美国关税调整对美日汽车贸易、美国汽车进口结构及美国汽车产业的影响。
问题3 美国主导全球半导体(芯片)产业,但制造能力薄弱。拜登政府于2022年8月通过《芯片与科学法案》,通过补贴推动先进半导体制造。然而,2025年特朗普政府认为关税比补贴更有效。同时,美国以国家安全和技术领先为由,对中国实施高端芯片出口管制。建立模型,综合考虑经济效率和国家安全因素,分析美国关税政策对国内半导体制造以及高、中、低端芯片贸易的影响。
问题4 提高关税税率短期内可能增加政府关税收入,但会减少贸易量,长期可能导致收入下降。建立模型分析美国关税调整对其关税收入的短期和中期影响,预测特朗普政府第二任期内关税调整带来的美国关税收入净变化。
问题5 美国加征关税可能引发贸易伙伴的反制措施。例如,中国已实施对等关税反制,并对稀土、锂电池等产品实施定向出口管制[9]。这些反制措施无疑将对美国对外贸易产生复杂影响,进而对美国国内农业、工业等多个部门产生全面而深远的作用,还可能影响美元、美国国债、虚拟货币等金融市场。选择或构建经济指标,建立模型分析美国关税调整对美国经济的短期和中期影响,并利用该模型评估"对等关税"政策是否能真正推动制造业回流。
术语表 -
对等关税(Reciprocal Tariffs):原指两个或多个国家通过双边或多边谈判相互降低或取消进口关税的制度。本文特指特朗普政府于2025年4月2日宣布的关税政策,名义上要求美国与贸易伙伴关税税率对等,实则对所有伙伴方征收10%的"最低基准关税",并对约60个贸易伙伴加征11%至50%不等的额外关税。
最惠国待遇(Most-Favored-Nation, MFN Treatment):指WTO成员方之间相互给予的关税和非关税优惠待遇,不得低于给予任何第三国的待遇。根据《1994年关税及贸易总协定》(GATT 1994)第一条规定,一成员方给予另一成员方的任何优惠,必须立即无条件地扩展至所有其他成员方。
数据说明所附数据提供2020年以来的美国对外贸易数据,来源于美国贸易与关税数据平台[6]。参赛团队不限于使用该数据,可从[4]等官方渠道获取额外贸易数据,或从[9]等来源获取非关税政策信息,也可使用合理的模拟数据。
题目中提供的数据仅仅为关税数据,即满足了每一问的研究主题,但是与之相关的数据均需要我们进行收集。
|------------------------|------------------|------------------|------------------|------------------|---------------|--------------|-----------|
| BZD数模社收集 亚太C题第一版本各题目数据 | | | | | | | |
| 问题1:大豆贸易相关指标 | 问题2:汽车贸易相关指标 | 问题3:半导体贸易相关指标 | 问题4:关税收入相关指标 | 问题5:美国经济影响相关指标 | | | |
| (2024-2025 月度数据) | (2020-2025 季度数据) | (2020-2025 季度数据) | (2020-2025 月度数据) | (2020-2025 月度数据) | | | |
| 美国量 | 总销量 | 墨西哥金额 | 集成电路产量 | 本土制造产能利用率 | 美国商品进口额 | 美国对外总出口额 | 制造业平均时薪 |
| 美国额 | 美国产 | 加拿大数量 | 12英寸晶圆产能 | 关税财政收入贡献额 | 基准关税税率 | 美国对外总进口额 | 美元指数DXY |
| 巴西量 | 墨西哥产 | 加拿大金额 | 高端芯片(≤14nm)进口额占比 | 单位制造成本变动率 | 关税总收入 | 对中国出口 | 10年期国债收益率 |
| 巴西额 | 加拿大产 | 美国对日本进口乘用车关税率 | 中低端芯片(≥14nm)出口额 | 高端芯片本土自给率 | 名义GDP | 对中国进口 | 比特币月末价格 |
| 阿根廷量 | 日本产 | USD/JPY 季度平均汇率 | 集成电路进口额 | 中低端芯片进口依赖度 | 工业生产指数 | 中国对等关税平均强度 | 实际GDP增长率 |
| 阿根廷额 | 德国产 | 日本汽车业对美FDI新增 | 集成电路出口额 | 关键原材料/设备进口依赖度 | 制造业PMI | 美国整体关税强度 | 失业率 |
| 总进口量 | 韩国产 | 日本政府对汽车业补贴 | 自给率估算 | 先进制程专利数量增长率 | | 农产品出口额 | CPI YoY |
| 大豆关税数值 | 其他 | 日本品牌在美国本土生产销量占比 | 关税 | 高端芯片技术研发投入强度 | BZD数模社收集 倒卖必究 | 农业增加值 | PPI YoY |
| BZD数模社收集 倒卖必究 | 日本数量 | 日本非关税应对策略指标 | 半导体制造业产值增长率 | BZD数模社收集 倒卖必究 | BZD数模社收集 倒卖必究 | 工业生产指数 | PCE YoY |
| | 日本金额 | | | | BZD数模社收集 倒卖必究 | 制造业生产指数 | 耐用品消费支出 |
| | 墨西哥数量 | | | | | 制造业增加值占GDP比重 | |
|-------|---------|---------------|----------|---------|-----------|-----------|
| 问题一数据 | 月份 | 中国大豆总进口量(mmt) | 美国量(mmt) | 美国额($B) | 阿根廷量(mmt) | 总进口量(mmt) |
| | 2025.3 | 8.8 | 1.95 | 1.05 | 0.55 | 8.8 |
| | 2025.4 | 9.8 | 0.63 | 0.34 | 0.57 | 9.8 |
| | 2025.5 | 12.46 | 0 | 0 | 1.46 | 12.46 |
| | 2025.6 | 11.2 | 0 | 0 | 1.8 | 11.2 |
| | 2025.7 | 10.5 | 0 | 0 | 1.7 | 10.5 |
| | 2025.8 | 10.2 | 0 | 0 | 1.5 | 10.2 |
| | 2025.9 | 9.8 | 0 | 0 | 1.17 | 12.13 |
| | 2025.10 | 6.8 | 0 | 0 | 1.3 | 6.8 |
|-------|-------------------|----------|--------|--------|-------|----------|----------|------------------------|
| 问题二数据 | 年份/季度 | 总销量(百万辆) | 美国产(%) | 日本产(%) | 其他(%) | 日本数量(万辆) | 日本金额($B) | USD/JPY 季度平均汇率 (日元/美元) |
| | 2024 Q3 | 3.98 | 54 | 8 | 1 | 25 | 10.4 | 160 |
| | 2024 Q4 | 3.85 | 54 | 8 | 1 | 23 | 9.7 | 152 |
| | 2025 Q1 | 3.85 | 56 | 7 | 1 | 28 | 11.5 | 150 |
| | 2025 Q2 | 4.02 | 57 | 7 | 2 | 22 | 9.2 | 148 |
| | 2025 Q3 | 3.68 | 59 | 6 | 2 | 15 | 6.5 | 145 |
| | 2025 Q4 (11月19日估) | 3.28 | 61 | 6 | 1 | 18 | 7.8 | 148.0 (截至11月) |
|-------|--------|------------|------------|---------------|--------------|---------|
| 问题五数据 | 年月 | 美国总出口(亿美元) | 美国总进口(亿美元) | 中国对美平均报复关税(%) | 美国整体有效关税率(%) | 农产品出口总额 |
| | 202503 | 278.5 | 339.1 | 84 | 3.8 | 13.8 |
| | 202504 | 289.4 | 340.5 | 125 | 15 | 11.5 |
| | 202505 | 282.1 | 341.2 | 125 | 16.2 | 10.2 |
| | 202506 | 279.8 | 342.8 | 125 | 16.8 | 9.8 |
| | 202507 | 281.2 | 343.5 | 125 | 17 | 9.5 |
| | 202508 | 280.8 | 340.4 | 125 | 17 | 9.8 |
| | 202509 | 282 | 342 | 10 | 16.6 | 10.2 |
| | 202510 | 285 | 345 | 10 | 16 | 11.5 |
| | 202511 | 288 | 346.5 | 10 | 15.8 | 12 |
通过网盘分享的文件:资料分享
链接: https://pan.baidu.com/s/1OICSbGnbLkvuVzQ_flsM5w?pwd=u5eg 提取码: u5eg