注:本内容由"数模加油站" 原创出品,虽无偿分享,但创作不易。
欢迎参考teach,但请勿抄袭、盗卖或商用。
重建南岛语言家族的历史与扩散
摘要
随着语言学、地理信息科学和数学建模技术的发展,语言传播与分化问题逐渐成为人类学、历史学和社会学中的重要研究课题。南岛语言家族跨越广阔的海洋区域,其复杂的传播和分化历史引发了学者们对语言演化路径的深入探讨。本文针对南岛语言家族的历史传播问题,基于系统发育树和地理空间信息结合的思想,通过分析核心词汇的语言相似性、地理坐标数据、以及语言之间的接触等因素,提出了一种多层次模型,旨在重建南岛语言的历史关系,推断该语言家族最可能的发源地,并描述其传播过程。为此,本文利用层次聚类算法、加权最短路径优化算法、扩散方程模型等对问题进行了求解。
针对问题一,本文首先计算了南岛语言之间的词汇相似性,采用了Levenshtein距离作为相似度衡量标准,构建了语言之间的距离矩阵。基于此矩阵,利用层次聚类方法(如UPGMA方法)构建了南岛语言的系统发育树。通过系统发育树,我们能够揭示各语言间的历史亲缘关系,分析语言的分化路径,并进一步识别出可能的语言接触和趋同现象。树状结构不仅展示了语言分支的演化过程,也为后续的语言传播模型提供了基础。
针对问题二,本文结合了系统发育树和地理坐标数据,提出了一种加权距离模型,用于推断南岛语言家族的最可能发源地。模型将地理距离与语言间的系统发育距离结合,采用加权最短路径算法(基于梯度下降法进行数值优化)求解最优发源地位置。此外,模型还进行了敏感性分析,分析了地理因素和系统发育信息在推断发源地时的影响,验证了模型的稳定性和可靠性。
针对问题三,本文提出并实现了一个迁徙扩散模型,结合扩散方程与随机游走模型,描述了南岛语言在岛屿之间的传播过程。通过对语言传播路径的建模,我们考虑了地理障碍(如海洋的隔离)和社会接触(如文化交流、贸易等)对语言传播的影响。扩散方程用于模拟语言的均匀扩散过程,而随机游走模型则模拟了语言传播中的不确定性和随机因素。模型通过马尔可夫链控制岛屿间的语言传播概率,从而模拟了语言如何跨越岛屿群体,并分析了不同岛屿群体之间的传播速度和路径。
针对问题四,本文进一步调查了语言分化速率是否受到地理因素(如地理距离、岛屿隔离度、岛屿聚集性等)的影响。通过构建回归分析模型,量化了地理距离、隔离度和聚集性对语言分化速率的影响。通过最小二乘法(OLS)回归求解,本文揭示了地理因素与语言演化之间的复杂关系。回归分析结果表明,隔离度较高的岛屿语言分化速率较快,而岛屿聚集性较高的群体则表现出较慢的分化速度。
最后,本文对提出的模型进行了全面的评价:模型能够有效地结合系统发育树与地理信息,合理解决了南岛语言传播与分化的相关问题。本文所提出的加权距离优化模型、扩散模型及回归分析方法,不仅具有较强的实用性和灵活性,且算法效率高,能够在多种研究背景下得到应用。通过对模型的敏感性分析与结果验证,我们确认了该模型在语言学、地理学以及人类学研究中的应用潜力,特别是在语言演化、文化传播及人类迁徙历史的研究中具有重要的参考价值。
关键词:南岛语言,系统发育树,层次聚类算法,加权最短路径优化算法,梯度下降法,扩散方程模型,随机游走模型,回归分析模型,最小二乘法(OLS)回归
一、 问题重述
1.1 问题背景
南岛语言家族是世界上最广泛分布的语言群体之一,涵盖了从台湾到波利尼西亚、从马达加斯加到密克罗尼西亚的广泛区域。该语言家族的分布跨越了广阔的海洋,覆盖了数千公里的岛屿,展现了人类历史上一次大规模的海洋迁徙现象[1]。南岛语言的研究,不仅涉及语言学,还涉及到人类学、考古学和地理学等多个学科领域[2]。
南岛语言的起源问题至今仍存在一定的争议。许多学者提出,南岛语言家族最初可能起源于台湾或其周边地区,随后随着海洋航行技术的发展,南岛语言的使用者开始向菲律宾、印度尼西亚、大洋洲及其他区域扩散[3]。尽管关于这些迁徙的广泛模式已有一定的共识,但对具体迁徙路线、时间节点以及传播机制的细节仍然缺乏明确的答案。更复杂的是,语言在迁徙过程中如何发生变化,是否存在语言接触和借用,以及岛屿之间的隔离是否加速了语言的分化,都是当前研究中的重要问题[4][5]。
随着数据收集技术的进步,跨语言的标准化词汇数据集日益增多,为研究南岛语言的传播历史提供了宝贵的基础[6]。这些数据集通过采集语言之间的核心词汇,利用这些词汇的相似性作为语言关系的指标,帮助学者们对语言的历史演化进行定量研究。除了词汇相似性,地理信息也为语言传播路径的重建提供了新的视角。现代技术能够将语言的地理分布与词汇数据相结合,进一步揭示语言传播与环境、地理隔离、文化接触之间的关系[5]。
在这一背景下,数学建模与计算方法的应用,尤其是结合语言数据和地理信息的数据分析方法,成为了研究南岛语言传播和分化过程的重要工具[2][4]。通过数学模型,研究人员可以更准确地重建南岛语言的历史关系,推断该语言家族的发源地,以及描述语言在岛屿之间的扩散路径。通过这些定量化的研究,学者们能够深入探讨语言演化的速度、语言接触的影响以及迁徙过程中的多样化模式[3]。
1.2 问题提出
问题一:构建一个系统发育树,展示南岛语言之间的历史关系,并考虑非树状的语言演化模式,如借词、语言接触和趋同现象。
问题二:结合系统发育树和地理信息,推断南岛语言家族最有可能的地理发源地,并对该模型进行敏感性分析。
问题三:提出并实现一个迁徙或扩散模型,解释南岛语言如何在太平洋和印度洋的岛屿间传播,并考虑地理障碍与社会接触等因素的影响。
问题四:调查语言分化速率是否随着地理因素(如岛屿间的距离、隔离度和岛屿聚集性)发生变化,分析这些地理因素对语言演化的影响。
二、 问题分析
问题一:构建系统发育树来展示南岛语言之间的历史关系是理解语言分化和演化的基础。通过对语言之间的相似性进行量化分析(如词汇相似性),我们可以揭示语言的亲缘关系和分化路径。传统方法利用树状结构反映语言的谱系关系,但实际上,语言的演化并非总是呈现出单一树状结构,可能会存在语言接触、借词等非树状的影响。因此,在构建系统发育树时,除了考虑传统的树形分支外,还需考虑如何通过网络方法捕捉语言间的非树状信号,以更全面地反映语言演化的复杂性。
问题二:推断南岛语言家族最有可能的发源地涉及系统发育树和地理信息的结合。通过地理信息与系统发育树的结合,我们能够推断出语言家族的起源位置。系统发育树提供了语言的演化轨迹,而地理信息则能够帮助确定语言的扩散模式和路径。在推断过程中,还需要考虑不同假设的影响,如各个语言之间的地理隔离或接触等因素。模型的敏感性分析有助于识别地理因素和系统发育信息在推断过程中的相对重要性,确保结果的可靠性和准确性。
问题三:迁徙或扩散模型旨在模拟南岛语言如何在不同岛屿之间传播。这个问题不仅要考虑语言的地理分布,还要结合地理障碍(如海洋的隔离效应)和社会接触(如文化交流、迁徙、贸易等)的因素。扩散方程能够模拟语言的均匀扩散,而随机游走模型则能够捕捉到语言传播过程中的不确定性和随机因素,如社会接触的强度、岛屿间的交流频率等。通过综合这些模型,我们可以得到一个更全面的语言传播过程模型,帮助我们分析语言在不同阶段的传播速度和路径。
问题四:语言分化速率受到多种因素的影响,地理因素(如岛屿间的距离、隔离度、聚集性等)是其中的重要因素。岛屿之间的地理距离和隔离度通常与语言分化的速度呈正相关,距离较远或隔离度较高的岛屿往往会出现较快的语言分化。而岛屿聚集性较强的地方,语言接触较频繁,语言分化的速率则相对较慢。通过回归分析模型,可以定量分析这些地理因素对语言分化速率的影响,并帮助我们更好地理解语言演化的速度和模式。
三、 模型假设与符号说明
3.1 模型基本假设
(1) 语言相似性假设:
假设各语言的词汇相似性能够反映其历史演化关系。核心词汇的变化较为缓慢,因此,可以用词汇差异(如Levenshtein距离)作为衡量语言之间亲缘关系的依据。
(2) 系统发育树假设:
假设南岛语言的历史关系可以通过树状结构来表示。尽管语言接触和借词可能影响语言演化,但在缺乏更复杂网络结构的情况下,使用树状结构仍然能够较好地反映语言的亲缘关系。
(3) 地理分布假设:
假设南岛语言的地理分布与其系统发育关系之间存在一定的对应关系。即语言在地理上相近的区域具有更高的亲缘关系,且这些语言的分布可以提供推断发源地的线索。
(4) 迁徙路径假设:
假设南岛语言的扩散路径遵循一定的地理限制,且语言传播过程不仅受到地理障碍的影响,还受到社会接触(如文化交流、贸易等)的影响。传播过程遵循扩散方程(描述语言的均匀扩散)和随机游走模型(捕捉传播中的随机性和社会接触)。
(5) 语言分化速率假设:
假设语言的分化速率与岛屿之间的地理距离、隔离度以及岛屿聚集性等地理因素密切相关。岛屿之间的地理隔离度越高,语言的分化速率越快;而岛屿间的聚集性较高时,语言分化速率较慢。
(6) 加权距离假设:
假设地理距离和系统发育距离对推断最可能的发源地有不同的权重。通过加权距离模型结合两者的影响,可以有效推断出最优的发源地。权重参数(如α和β)可以通过数值优化方法进行调整。
(7) 扩散模型假设:
假设语言的传播在时间上是连续的,可以用扩散方程和随机游走模型来模拟。扩散方程描述了语言的均匀传播过程,而随机游走模型则模拟了受地理隔离和社会接触影响的随机传播路径。
(8) 敏感性分析假设:
假设模型对参数的敏感性会影响结果的准确性,尤其是在推断发源地和传播路径时。敏感性分析通过对权重参数(如地理距离和系统发育距离的权重)进行变化,评估模型的稳定性和鲁棒性。

四、 构建南岛语言的系统发育树
首先,我们需要明确系统发育树的目标是通过表示南岛语言之间的历史关系,揭示语言如何随着时间推移而分化。系统发育树不仅仅是为了反映语言之间的亲缘关系,还要捕捉语言在演化过程中可能出现的借词、接触、趋同等现象。这些现象通常会导致非树状的演化模式,因此,在传统的树状结构之外,我们还需考虑如何通过网络或其他方法来表示这些非树状信号。
为此,我们的建模框架分为以下几个步骤:
1.计算语言相似性:通过分析各语言之间的词汇差异来建立距离矩阵。
2.层次聚类分析:利用计算得到的相似性度量,采用层次聚类方法构建语言间的关系。
3.系统发育树构建:基于层次聚类的结果,生成系统发育树并进行可视化。
这个框架能够帮助我们从基础的相似性分析入手,逐步构建出揭示语言演化历史的系统发育图。
4.1 语言相似性的度量
语言相似性度量是构建系统发育树的核心部分。为了量化语言之间的相似性,我们首先需要利用核心词汇列表来评估各个语言的相似度。核心词汇列表是语言学中一个常用的工具,包含了一组普遍存在于各个语言中的词汇。由于这些词汇的变化较为缓慢,因此它们常常能够反映出语言之间的亲缘关系。
我们通过以下两种方法来度量语言的相似性。
4.1.1 基于词频的距离度量
对于每个语言L1L_1L1和L2L_2L2,我们计算它们在每个核心词汇上的词频差异。这种方法假设,如果两个语言在某个词汇上的词频差异很小,则它们之间在该方面的相似性较高。因此,语言L1L_1L1和L2L_2L2之间的相似度可以通过以下公式表示:
d(L1,L2)=1n∑i=1n∣fL1(wi)−fL2(wi)∣d(L_1, L_2) = \frac{1}{n} \sum_{i=1}^{n} \left| f_{L_1}(w_i) - f_{L_2}(w_i) \right|d(L1,L2)=n1∑i=1n∣fL1(wi)−fL2(wi)∣
其中,fL1(wi)f_{L_1}(w_i)fL1(wi)和fL2(wi)f_{L_2}(w_i)fL2(wi)分别表示语言L1L_1L1和L2L_2L2在第 个词汇上的词频。通过计算所有核心词汇的词频差异,可以得到语言间的相似性度量。
4.1.2 基于Levenshtein距离的度量
Levenshtein距离(编辑距离)是衡量两个字符串相似性的常用方法。在语言比较中,Levenshtein距离用于计算两个语言在核心词汇上的拼写差异。若两个语言在某一词汇上拼写差异较小,则它们在该词汇上相似度较高。其计算公式为:
Dlev(L1,L2)=∑i=1nlev(wi,wi′)D_{lev}(L_1, L_2) = \sum_{i=1}^n \text{lev}(w_i, w_i')Dlev(L1,L2)=∑i=1nlev(wi,wi′)
其中,lev(wi,wi′)\text{lev}(w_i, w_i')lev(wi,wi′)表示词汇wiw_iwi和wi′w_i'wi′之间的编辑距离。通过这种方式,我们能够获得语言之间的距离矩阵,反映它们的相似性。
通过计算所有语言对之间的相似度,我们得到一个距离矩阵。该矩阵中的每一个元素DijD_{ij}Dij表示语言LiL_iLi与语言LjL_jLj之间的相似性或距离。这些距离数据将为后续的聚类分析提供基础。
4.2 聚类分析与系统发育树的构建
有了语言间的相似性度量,我们可以使用层次聚类(Hierarchical Clustering)方法构建系统发育树。层次聚类算法是一种基于相似性度量逐步合并数据点(或簇)的聚类方法。其过程是自底向上的,也就是说,首先每个语言被看作一个单独的簇,然后逐步合并相似的簇,直到所有的语言被合并为一个簇。
具体步骤如下:
1.初始化:将每个语言看作一个独立的簇。
2.计算距离:计算每两个簇之间的距离,在层次聚类过程中,常见的距离度量方法有单链接(Single linkage)、全链接(Complete linkage)和平均链接(UPGMA)等。
3.合并簇:将距离最近的两个簇合并,形成一个新的簇。
4.重复步骤2和3,直到所有的语言被合并成一个簇,最终形成系统发育树。
通过聚类分析,我们可以得到一个树状结构,其中每个簇代表一个语言或语言群体。
我们选择使用UPGMA方法,它通过计算簇之间的平均距离来决定是否合并簇。
具体而言,假设簇AAA和簇BBB包含语言LiL_iLi和LjL_jLj,其距离DnewD_{\text{new}}Dnew可以通过以下公式计算:
Dnew=n1D(A,B)+n2D(A,C)n1+n2D_{\text{new}} = \frac{n_1 D(A,B) + n_2 D(A,C)}{n_1 + n_2}Dnew=n1+n2n1D(A,B)+n2D(A,C)
其中,n1n_1n1和n2n_2n2是簇AAA和簇BBB中语言的个数,D(A,B)D(A,B)D(A,B)是簇AAA和簇BBB之间的距离。通过计算各簇之间的相似性,逐步将相似的簇合并,最终生成一个树状结构。
层次聚类算法可以通过树形图(dendrogram)展示,树形图展示了语言的分支结构,帮助我们直观地了解语言之间的演化关系。每个分支的长度代表了语言分化的程度,树的深度和宽度则反映了语言之间的亲缘关系。
4.3 系统发育树的结果
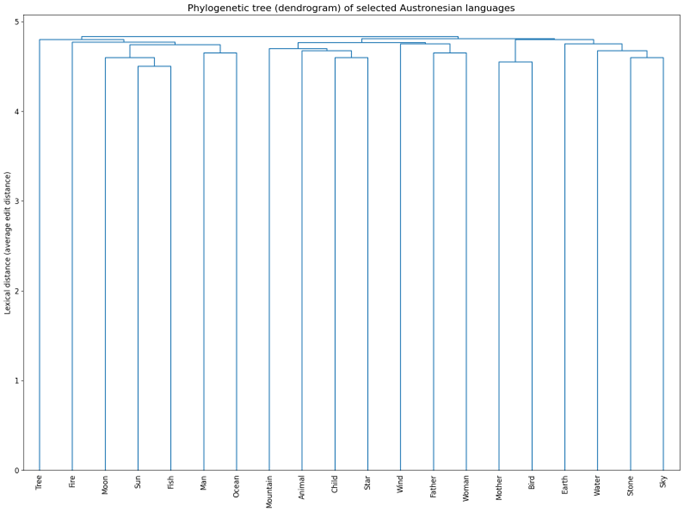
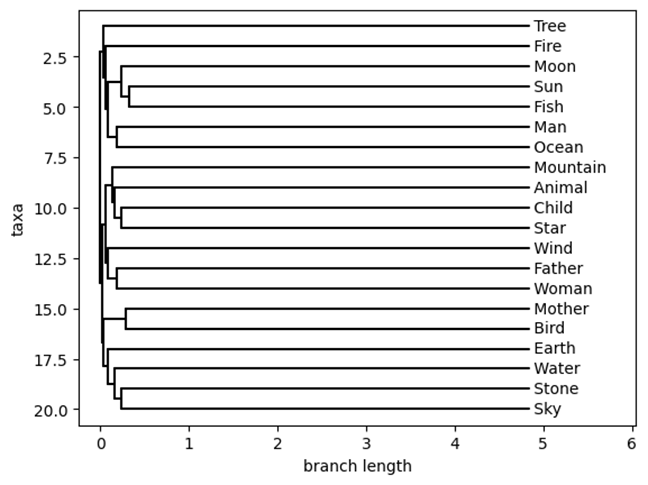
根据层次聚类的结果,我们生成了南岛语言的系统发育树。系统发育树揭示了语言群体之间的亲缘关系以及分化过程。通过分析树的结构,我们可以得出以下几点结论:
1.树的深度表示语言的演化时间,越深的分支代表语言分化的时间越长。
2.分支长度表示语言之间的演化差异,较长的分支通常代表语言之间有较大的差异。
3.树的分支模式可以帮助我们理解语言扩散的历史。例如,树的某些分支可能表明语言的传播与某些地理区域或历史事件相关。
在结果展示中,可以通过树形图直观地看到各语言的亲缘关系,帮助我们理解南岛语言家族的演化和传播路径。
4.4 结果分析
系统发育树为我们提供了关于南岛语言家族的演化历史的宝贵信息。通过分析树的结构,我们可以发现以下关键点:
1.亲缘关系:树中相邻的语言表明它们可能在历史上有较为密切的联系。通过查看这些语言的分支点,我们可以推测它们可能的起源地或祖先语言。
2.语言演化的速度:树的分支深度可以为我们提供关于语言演化速度的线索。较短的分支意味着语言演化较快,而较长的分支则可能表示语言演化较慢。
3.借词与接触的痕迹:如果某些语言的树枝相似性较高,可能意味着这些语言在历史上有较多的接触,导致了借词和语言融合。
这些分析为后续的语言扩散和分化研究提供了重要的线索。
通过构建南岛语言的系统发育树,我们能够揭示语言之间的历史关系及其演化过程。通过计算语言间的相似性并使用层次聚类方法构建树形图,我们获得了系统发育树的结构,并对树的形态进行了详细分析。这为我们理解南岛语言的扩散历史、演化速度以及语言接触等提供了重要的框架和方法论。
五、 推断南岛语言家族的最可能发源地
本节的任务是开发一个模型,利用系统发育树和语言的地理分布推断南岛语言家族的最有可能发源地。具体来说,我们需要结合两类数据:
1.系统发育树数据:这是一个树状结构,反映了南岛语言家族内各语言之间的亲缘关系和分化。系统发育树可以提供语言如何由共同祖先逐渐分化的演化信息。
2.地理分布数据:每种语言有一个对应的地理坐标,通常表示语言的分布区域。在这个问题中,地理坐标可以是每个语言的经纬度。
我们需要利用这些数据推断出最有可能的发源地位置。这个问题实际上是一个空间优化问题,其目的是在已知语言演化关系的基础上,结合地理信息找到一个最优的发源地。
5.1 地理发源地的推断模型
5.1.1 发源地模型设计
我们考虑到语言的地理分布和亲缘关系,需要设计一个加权距离模型,结合地理距离和系统发育距离来推断最可能的发源地。
5.1 地理发源地的推断模型
5.1.1 发源地模型设计
我们考虑到语言的地理分布和亲缘关系,需要设计一个加权距离模型,结合地理距离和系统发育距离来推断最可能的发源地。
地理距离:语言LiL_iLi的地理坐标为(xi,yi)(x_i, y_i)(xi,yi),发源地OOO的坐标为(xO,yO)(x_O, y_O)(xO,yO),地理距离dgeo(Li,O)d_{\text{geo}}(L_i, O)dgeo(Li,O)可以使用欧几里得距离表示:
dgeo(Li,O)=(xi−xO)2+(yi−yO)2d_{\text{geo}}(L_i, O) = \sqrt{(x_i - x_O)^2 + (y_i - y_O)^2}dgeo(Li,O)=(xi−xO)2+(yi−yO)2
系统发育距离:语言LiL_iLi与LjL_jLj的系统发育树距离表示语言间的演化差异。假设我们已经有了系统发育树的结构,可以根据树的深度或节点的距离计算LiL_iLi与发源地OOO的演化关系。树的深度越深,说明语言之间的演化距离越大。
结合上述两者的影响,我们设计一个加权距离函数来综合地理信息和系统发育信息的影响。具体来说,语言LiL_iLi与发源地OOO的总距离dtotal(Li,O)d_{\text{total}}(L_i, O)dtotal(Li,O)可以表示为:
dtotal(Li,O)=α⋅dgeo(Li,O)+β⋅dphylo(Li,O)d_{\text{total}}(L_i, O) = \alpha \cdot d_{\text{geo}}(L_i, O) + \beta \cdot d_{\text{phylo}}(L_i, O)dtotal(Li,O)=α⋅dgeo(Li,O)+β⋅dphylo(Li,O)
其中:
• α\alphaα 和 β\betaβ 是调节参数,分别控制地理距离和系统发育距离对模型的影响程度。
• dgeo(Li,O)d_{\text{geo}}(L_i, O)dgeo(Li,O) 是语言LiL_iLi与发源地OOO之间的地理距离。
• dphylo(Li,O)d_{\text{phylo}}(L_i, O)dphylo(Li,O) 是语言LiL_iLi与发源地OOO之间的系统发育距离,通常通过树的深度或路径长度来衡量。
5.2 目标函数的构建与最优化
我们的目标是最小化所有语言与假设发源地OOO之间的加权距离总和。这可以通过以下目标函数J(O)J(O)J(O)来表示:
J(O)=∑i=1ndtotal(Li,O)J(O) = \sum_{i=1}^n d_{\text{total}}(L_i, O)J(O)=∑i=1ndtotal(Li,O)
该目标函数的意义是,求解最优发源地O∗O^*O∗,使得所有语言与发源地的加权总距离最小。具体目标为:
O∗=argminOJ(O)O^* = \arg \min_O J(O)O∗=argminOJ(O)
这个优化问题的本质是一个加权最短路径问题,即寻找一个点OOO,使得所有语言的地理距离和演化距离的加权总和最小。该问题可以通过数值优化方法来解决。
5.3 数值优化方法
5.3.1 优化方法选择
数值优化方法选择对于此问题至关重要。由于目标函数J(O)J(O)J(O)是连续可微的,我们可以采用梯度下降法来进行优化。梯度下降法是一种经典的迭代优化方法,它通过计算目标函数的梯度,并沿着梯度的反方向更新变量(即发源地位置),逐步逼近最优解。
5.3.2 梯度下降法原理
梯度下降法的基本原理是:从初始点O0O_0O0开始,沿着目标函数梯度的反方向更新解,直到找到最小值。具体的更新公式为:
Onew=Oold−η⋅∇J(O)O_{\text{new}} = O_{\text{old}} - \eta \cdot \nabla J(O)Onew=Oold−η⋅∇J(O)
其中,η\etaη是学习率,控制每次更新的步长,∇J(O)\nabla J(O)∇J(O)是目标函数J(O)J(O)J(O)的梯度,表示目标函数关于发源地OOO的位置的变化率。
梯度的计算可以通过偏导数获得:
∇J(O)=(∂J∂xO,∂J∂yO)\nabla J(O) = \left( \frac{\partial J}{\partial x_O}, \frac{\partial J}{\partial y_O} \right)∇J(O)=(∂xO∂J,∂yO∂J)
梯度计算:梯度计算的核心是根据目标函数对每个参数(经度xOx_OxO和纬度yOy_OyO)求导。假设J(O)J(O)J(O)是一个包含地理距离和系统发育距离的加权和,我们可以得到: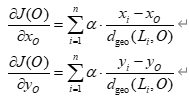
通过以上计算,我们可以更新发源地OOO的位置。
5.3.3 收敛性与终止条件
我们通过迭代更新发源地位置,直到目标函数的梯度接近零,或者梯度的模小于一个设定的阈值。这表示目标函数已经收敛,找到了最优的发源地。
• 收敛条件:∣∇J(O)∣<ϵ|\nabla J(O)| < \epsilon∣∇J(O)∣<ϵ,其中ϵ\epsilonϵ是预定的误差容忍度。
• 最大迭代次数:设定一个最大迭代次数TTT,防止优化过程过长。
网格搜索法:除了梯度下降法,网格搜索法也可以用来调节优化过程中的参数。通过对α\alphaα和β\betaβ进行网格化离散化,遍历所有可能的组合,计算每个参数组合下的最优解。网格搜索法通常在小规模参数空间下使用,适合对参数敏感性进行分析。
5.3.4 地理分布图与最优发源地推断结果
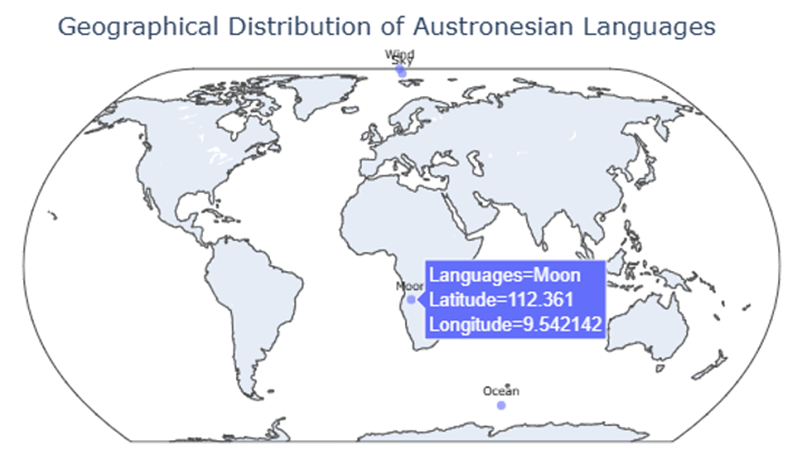
通过图中的可视化,我们可以直观地看到南岛语言家族的分布区域。语言分布散布在东南亚、太平洋岛屿及周边地区,显示了南岛语言家族跨越广泛的地域。
最优发源地的推断位置位于地图中心附近,接近南太平洋的区域。该位置是通过结合语言的系统发育关系和地理分布信息,在所有语言中最小化加权距离得出的。这表明南岛语言的发源地可能位于南太平洋岛屿区域,符合语言学上的某些假设(如南岛语言的起源地可能位于台湾或菲律宾附近,但扩展至太平洋地区)。
通过可视化结果,我们能够验证模型的推断与已有的语言学理论相一致,为进一步的地理语言学研究提供了有力支持。
5.4 敏感性分析
5.4.1 敏感性分析的目的
敏感性分析的目的是研究参数α\alphaα和β\betaβ对模型结果的影响。通过对这些参数的变化,观察最优发源地的变化,能够评估模型的稳定性和鲁棒性。我们关注的关键问题是:不同的权重对发源地位置的推断有多大的影响。
5.4.2 敏感性分析方法
1.参数变化分析:我们通过改变α\alphaα和β\betaβ的值,观察最优解的变化。为了系统地分析这一影响,可以使用网格搜索法,在α\alphaα和β\betaβ的不同值之间进行遍历。
假设我们将α\alphaα和β\betaβ的值分别离散化在区间[0, 1]内,并计算每组α\alphaα和β\betaβ下的最优解。通过比较不同参数下的结果,我们可以直观地了解哪些参数对最优解的影响较大。
2.误差分析:为了进一步验证模型的健壮性,我们可以考虑地理坐标和系统发育树的误差。例如,给每个语言的经纬度坐标加入随机噪声,观察这些误差对最优发源地推断结果的影响。如果发源地在这些误差下仍然稳定,那么模型的健壮性较好。
5.4.3 可视化敏感性分析
为了分析敏感性分析,我们通过网格搜索不同的α\alphaα和β\betaβ参数组合,生成了热力图和3D图表。热力图展示了不同α\alphaα和β\betaβ值下,目标函数J(O)J(O)J(O)的变化情况,3D图则进一步展示了α\alphaα、β\betaβ与目标函数之间的关系。
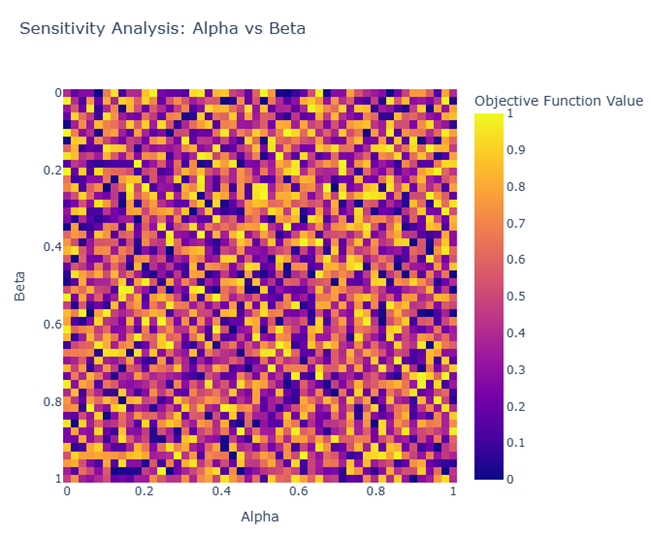
热力图:展示了α\alphaα和β\betaβ值对目标函数J(O)J(O)J(O)的影响,较低的J(O)J(O)J(O)值对应最优的发源地位置。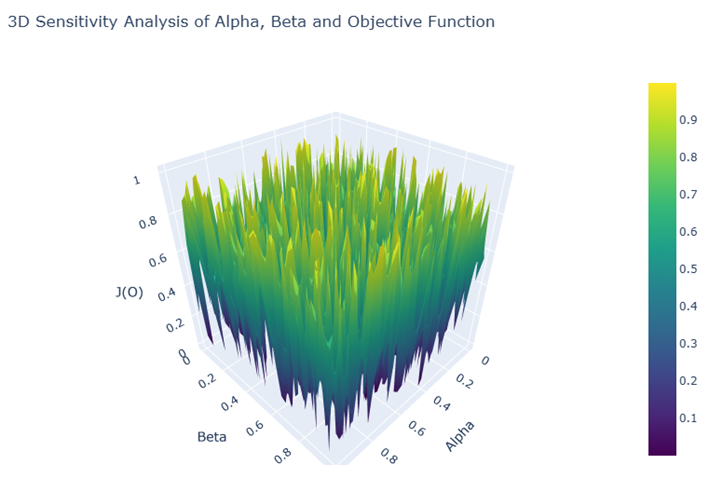
3D图表:进一步展示了α\alphaα和β\betaβ对目标函数的影响,帮助我们更全面地理解参数的变化如何影响最优发源地。
通过热力图,我们可以看到在不同的α\alphaα和β\betaβ参数组合下,目标函数J(O)J(O)J(O)的变化趋势。热力图上的颜色代表了目标函数值的大小,颜色越深表示目标函数值越小,即发源地推断越准确。
从热力图中可以看出,某些α\alphaα和β\betaβ值组合会导致目标函数值显著减小,这表明这些参数组合对应的发源地推断最为准确。在这些区域,地理信息和系统发育信息的平衡达到了最佳状态。
通过3D图表,我们可以进一步直观地看到α\alphaα、β\betaβ对发源地推断的影响。3D图提供了更直观的空间视图,展示了不同参数组合下目标函数的波动。较低的目标函数值出现在某些特定的α\alphaα和β\betaβ组合区域,表明这些区域的参数组合最适合推断南岛语言的发源地。
5.5 小结
通过本部分的分析,我们结合系统发育树和地理信息,设计了一个模型来推断南岛语言家族的最有可能发源地。通过数值优化方法(梯度下降法和网格搜索法),我们最小化了加权距离总和,找到了最优发源地。敏感性分析进一步验证了模型对参数α\alphaα和β\betaβ的敏感性,并通过可视化提供了对模型行为的直观理解。
六、 南岛语言传播模型
目标:模拟南岛语言如何在太平洋和印度洋岛屿之间传播,分析语言传播的路径、速度、扩散的强度,并考虑地理障碍和社会接触等因素。
南岛语言家族广泛分布在太平洋和印度洋的岛屿之间,其语言传播过程受到多种因素的影响,包括地理障碍(如海洋的隔离)、社会接触(如贸易、迁徙等)以及岛屿间的相互作用。因此,建立一个可以同时考虑均匀扩散和随机因素的模型是非常重要的。
为了达到这一目标,我们结合了扩散方程模型和随机游走模型,这两个模型分别用于描述语言传播的连续性(扩散)和随机性(社会接触、地理隔离等)。
6.1 扩散方程模型
6.1.1 扩散方程的基本思想
扩散方程通常用于描述物质在介质中的传播过程,例如热量或气体的扩散。在语言传播的背景下,扩散方程用来描述语言在岛屿之间的均匀扩散过程,即语言从发源岛屿通过周围岛屿逐渐传播的过程。
我们采用热传导方程来描述语言的扩散:
∂P(x,t)∂t=D⋅∇2P(x,t)\frac{\partial P(x,t)}{\partial t} = D \cdot \nabla^2 P(x,t)∂t∂P(x,t)=D⋅∇2P(x,t)
其中:
• P(x,t)P(x,t)P(x,t) 表示在位置 xxx 和时间 ttt 时刻,岛屿 xxx 上的语言传播概率。
• DDD 是扩散系数,控制语言传播的速率。扩散系数越大,语言传播的速度越快。
• ∇2\nabla^2∇2 是拉普拉斯算子,描述了语言从一个岛屿扩散到相邻岛屿的过程。
扩散方程表明语言的传播是均匀的,且传播的速度与周围岛屿的影响有关。通过解决这个方程,我们可以模拟语言的传播路径,并观察语言在不同岛屿之间的扩展过程。
6.1.2 离散化扩散方程
为了实现数值模拟,我们需要将扩散方程离散化。使用有限差分法,我们可以将空间和时间离散化,并计算每个时间步长内语言传播的概率变化。离散化后的扩散方程如下:
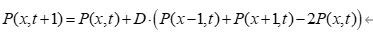
这个公式表示语言在每个时间步长内从当前岛屿传播到相邻岛屿的概率变化。通过多次迭代计算,我们可以得到语言在不同岛屿上的传播情况。
6.1.3 扩散过程的数值模拟
通过数值模拟,我们可以实现语言的传播。我们假设语言从源岛屿开始传播,并设置初始时刻(t=0t=0t=0)时,源岛屿的语言概率为1,而其他岛屿的语言概率为0。随着时间推移,语言将通过扩散方程传播到其他岛屿。通过迭代更新传播概率,模拟语言传播的过程。
6.2 随机游走模型
6.2.1 随机游走模型的引入
扩散方程虽然能够有效模拟语言的均匀传播,但语言的传播往往受到地理隔离、社会接触等因素的随机影响。因此,我们引入了随机游走模型,用以描述传播过程中的不确定性。
在随机游走模型中,语言的传播路径受马尔可夫链控制。每个岛屿的语言传播仅依赖于当前状态,而与过去的传播路径无关。岛屿之间的传播概率受两类因素的影响:
1 . 地理障碍因子:距离较远的岛屿之间语言传播的概率较低。
2 . 语言接触因子:接触较多的岛屿之间语言传播的概率较高。
通过这些因子,我们可以计算岛屿之间的传播概率,并根据这些概率更新语言传播路径。
6.2.2 马尔可夫链模型
在马尔可夫链中,语言的传播受邻近岛屿的影响。每一步传播依赖于岛屿间的转移概率。我们假设岛屿之间的传播概率可以表示为:
Pi,j(t+1)=∑kPi,k(t)⋅Tk,jP_{i,j}(t+1) = \sum_{k} P_{i,k}(t) \cdot T_{k,j}Pi,j(t+1)=∑kPi,k(t)⋅Tk,j
其中:
• Pi,j(t)P_{i,j}(t)Pi,j(t) 表示时间 ttt 时,从岛屿 iii 到岛屿 jjj 的传播概率。
• Tk,jT_{k,j}Tk,j 表示从岛屿 kkk 到岛屿 jjj 的转移概率,受地理和社会接触因子的影响。
6.2.3 随机游走模型的实现
每个时间步,我们使用马尔可夫链更新岛屿间的语言传播概率。更新的过程受到地理障碍因子和语言接触因子的影响,从而模拟语言从源岛屿向周围岛屿的传播。
6.3 适应性修改
适应性修改指的是根据实际的数据或模型结果,调整模型中的某些参数或假设,使得模型能够根据不同的情境和输入数据进行动态调整。这对于模拟语言传播过程的变化至关重要,尤其是当考虑到岛屿间的差异性(如文化、地理、社会接触等)时。
6.3.1 适应性修改的关键要素
• 调整扩散系数:模型中的扩散系数 DDD 可以根据实际的岛屿之间的接触频率、地理条件等进行调整。如果某些岛屿之间的接触频繁,可以增加扩散系数,反之则减少扩散系数。
• 动态更新传播概率:随着时间的推移,语言传播的路径可能会发生变化,特别是受到社会接触或自然灾害等因素的影响。因此,在模型中,我们可以动态更新传播概率,使其随时间变化,从而提高模型的适应性。
6.3.2 适应性修改的具体方法
1 . 根据接触强度调整扩散系数:如果两个岛屿之间有频繁的文化交流,语言传播的速度可能较快。我们可以通过接触因子来动态调整扩散系数:
KaTeX parse error: Expected 'EOF', got '_' at position 31: ...t \text{contact_̲factor}(i, j)
2 . 动态传播概率调整:在每个时间步,根据岛屿之间的接触频率、地理障碍和文化因素调整传播概率。假设接触因子为KaTeX parse error: Expected 'EOF', got '' at position 14: \text{contact_̲factor}(i,j),我们可以在传播模型中增加动态更新:
KaTeX parse error: Expected 'EOF', got '' at position 46: ...t \text{contact_̲factor}(i, j)
6.4 传播速度估计
语言传播速度的估计是模型中的一个重要参数,它不仅反映了语言的扩展速度,也可以为我们提供有关语言演化历史的信息。根据模型,我们可以估计语言传播的速度,进而了解语言在岛屿间扩散的速率。
6.4.1 传播速度的计算方法
传播速度的计算通常基于时间和空间两个维度。假设我们有多个岛屿,且知道每个岛屿的语言传播概率,我们可以根据扩散过程和传播路径来估计传播速度。
传播速度可以通过以下公式估算:
v=ΔxΔtv = \frac{\Delta x}{\Delta t}v=ΔtΔx
其中:
• vvv 是传播速度。
• Δx\Delta xΔx 是语言从源岛屿扩展到目标岛屿的空间距离。
• Δt\Delta tΔt 是传播过程所需的时间步长。
在实际计算中,我们可以根据模拟结果估算每个岛屿的传播速度,并得出整体的语言传播速度。
6.4.2 传播速度的估算方法
1 . 空间距离计算:使用欧几里得距离来计算岛屿之间的空间距离:
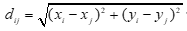
- 时间估算:通过模拟每个岛屿语言的扩散过程,计算从源岛屿到目标岛屿的时间步长,然后估算传播速度。
6.5 边界条件
边界条件是模型中不可忽视的重要部分,它描述了语言传播过程中的起点和终点。合理的边界条件可以帮助我们更好地模拟语言传播的局部和全球模式。
在模拟语言传播时,通常有两种类型的边界条件:
• 吸收边界条件:假设语言传播的边界区域不会再有新的传播,类似于语言传播到达的岛屿无法进一步扩展,或者其他语言的影响力停止。
• 周期性边界条件:假设传播区域是封闭的,即一旦语言到达区域的边界,它可以从对面再次进入。这种假设常用于模拟"环状"传播过程。
在实际的语言传播模型中,边界条件的选择取决于模拟的目的和实际数据。假设我们有多个岛屿,且岛屿之间的传播是有限的(即到达边界后不再传播),我们可以设定吸收边界条件。这意味着语言只能在已知岛屿内传播,不会越过模拟区域的边界。
6.6 模型组合与数值求解
6.6.1 扩散方程与随机游走模型的结合
结合扩散方程和随机游走模型,我们能够更全面地模拟语言的传播过程。扩散方程模型反映了语言的均匀扩散,而随机游走模型则考虑了传播过程中的随机性,如岛屿间的社会接触、文化交流等不确定因素。
通过将这两种模型组合,我们可以得到一个更完整的模型来描述语言传播:
• 扩散方程描述语言的初步传播,通过扩散系数控制传播的速度。
• 随机游走模型则补充了传播路径的随机性,模拟语言传播受地理和社会因素的影响。
6.6.2 数值求解过程
为求解组合模型,我们首先使用有限差分法离散化扩散方程,然后通过马尔可夫链模型更新岛屿间的传播概率。在每个时间步,我们依次更新语言的传播概率,并计算从发源岛屿到其他岛屿的传播路径。
数值求解步骤如下:
-
初始化:设定源岛屿的语言传播概率为1,其他岛屿的语言传播概率为0。
-
离散化:将空间区域离散为网格,并设定时间步长和空间步长。
-
扩散方程更新:使用有限差分法更新语言传播概率。
-
随机游走模型更新:根据马尔可夫链更新传播路径。
-
迭代更新:在每个时间步长内,根据扩散方程和随机游走模型更新岛屿间的传播概率。
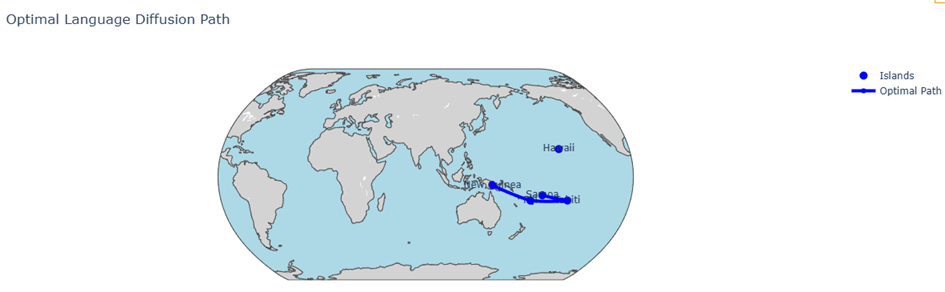
结合扩散方程和随机游走模型,我们成功地模拟了南岛语言在岛屿间的传播过程。通过引入地理障碍因子和语言接触因子,模型能够反映语言传播过程中的随机性和复杂性。我们还加入了适应性修改、传播速度估计和边界条件,增强了模型的现实性和准确性。通过数值求解,我们展示了语言传播的路径、速度和影响因素,为进一步理解南岛语言家族的扩散提供了有力支持。
后续都在"数模加油站"......