人工智能-python-深度学习-经典网络模型-LeNets5

文章目录

• [LeNet-5（详解）------ 从原理到 PyTorch 实现（含训练示例）](#LeNet-5（详解）—— 从原理到 PyTorch 实现（含训练示例）)
• • 简介
  • [LeNet-5 的核心思想](#LeNet-5 的核心思想)
  • [LeNet-5 逐层结构详解](#LeNet-5 逐层结构详解)
  • 逐层计算举例
  • • [📌 输入层](#📌 输入层)
    • [📌 C1 卷积层](#📌 C1 卷积层)
    • [📌 S2 池化层](#📌 S2 池化层)
    • [📌 C3 卷积层](#📌 C3 卷积层)
    • [📌 S4 池化层](#📌 S4 池化层)
    • [📌 C5 卷积层](#📌 C5 卷积层)
    • [📌 F6 全连接层](#📌 F6 全连接层)
    • [📌 输出层](#📌 输出层)
  • 关键设计点解析
  • [PyTorch 实现 LeNet-5](#PyTorch 实现 LeNet-5)
  • 训练与评估
  • 实验扩展
  • 总结
  • 参考资料

---

LeNet-5（详解）------ 从原理到 PyTorch 实现（含训练示例）

简介

LeNet-5 是 Yann LeCun 在 1998 年提出的一种经典卷积神经网络（CNN），最早用于 手写数字识别（MNIST 数据集） 。它是深度学习的奠基网络之一，对后续的 AlexNet、VGG、ResNet 等深度网络有重要启发。

论文：Gradient-based learning appl ied to document re cognition
中文可参考： 论文

👉 本文目标：通过 逐层解析 LeNet-5 的思想 ，并在 PyTorch 中实现与训练 ，让你从 理论 → 实践 → 实验扩展 全面理解这一经典网络。

---

LeNet-5 的核心思想

1. 局部感受野（Local Receptive Field）

   每个神经元只连接输入图像的一小块区域，减少计算量并提取局部特征。

2. 权值共享（Weight Sharing）

   卷积层使用相同的卷积核（Filter）在整张图像上滑动，极大减少参数数量。

3. 下采样（Subsampling / Pooling）

   使用平均池化降低特征图尺寸，保留关键信息，减少过拟合。

---

LeNet-5 逐层结构详解

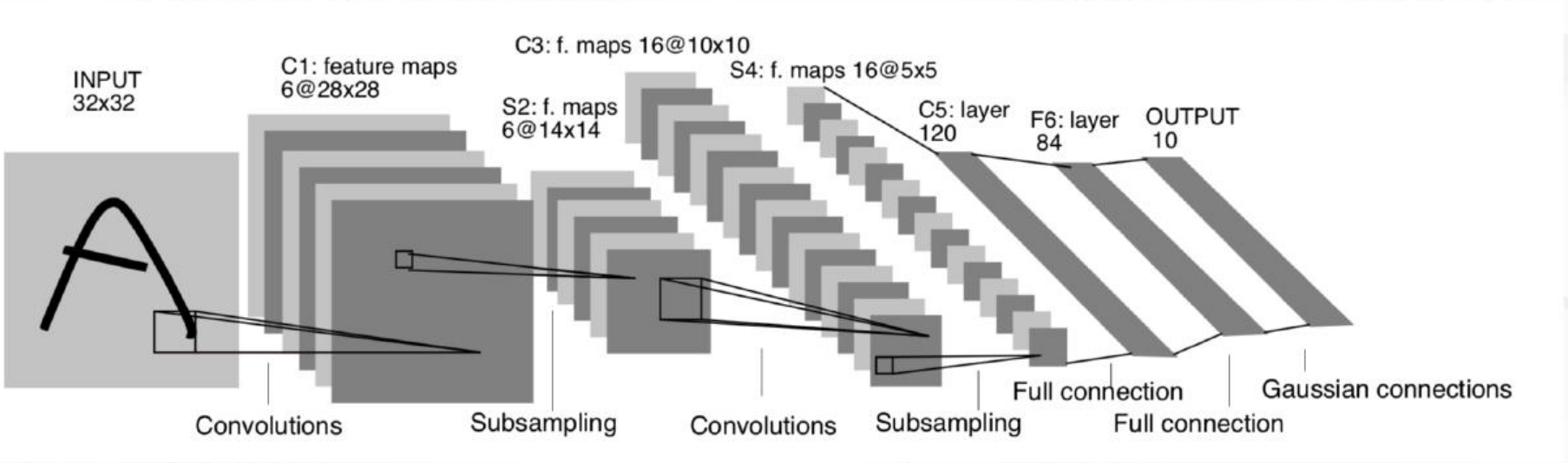
输入为 32×32 灰度图像 （MNIST 原本是 28×28，论文中补 0 填充到 32×32）。一共七层，3个卷积层，2个池化层，2个全连接层

层级	类型	输入尺寸	核心操作	输出尺寸	参数量
输入层	Image	32×32×1	-	32×32×1	0
C1	卷积层	32×32×1	6 个 5×5 卷积核，stride=1	28×28×6	156
S2	池化层	28×28×6	6 个 2×2 平均池化，stride=2	14×14×6	12
C3	卷积层	14×14×6	16 个 5×5 卷积核（部分连接）	10×10×16	≈1516
S4	池化层	10×10×16	16 个 2×2 平均池化，stride=2	5×5×16	32
C5	卷积层	5×5×16	120 个 5×5 卷积核（全连接方式）	1×1×120	48120
F6	全连接	120	全连接到 84 个神经元	84	10164
输出层	Softmax	84	全连接到 10 类	10	850

---

逐层计算举例

卷积与池化的计算公式：

• 卷积层公式：

  O = W − F + 2 P S + 1 O = \frac{W - F + 2P}{S} + 1 O=SW−F+2P+1

  其中：

  • W W W：输入特征图大小
  • F F F：卷积核大小
  • P P P：Padding
  • S S S：步长 (stride)
  • O O O：输出特征图大小

• 池化层公式：同卷积公式，只是用池化窗口替换卷积核。

---

📌 输入层

输入：32×32×1（单通道灰度图）

---

📌 C1 卷积层

• 输入：32×32×1

• 卷积核：6 个 5×5，stride=1，padding=0

• 计算：

  O = 32 − 5 + 0 1 + 1 = 28 O = \frac{32 - 5 + 0}{1} + 1 = 28 O=132−5+0+1=28

• 输出：28×28×6

---

📌 S2 池化层

• 输入：28×28×6

• 池化窗口：2×2，stride=2

• 计算：

  O = 28 − 2 2 + 1 = 14 O = \frac{28 - 2}{2} + 1 = 14 O=228−2+1=14

• 输出：14×14×6

---

📌 C3 卷积层

• 输入：14×14×6

• 卷积核：16 个 5×5，stride=1，padding=0（部分连接）

• 计算：

  O = 14 − 5 1 + 1 = 10 O = \frac{14 - 5}{1} + 1 = 10 O=114−5+1=10

• 输出：10×10×16

---

📌 S4 池化层

• 输入：10×10×16

• 池化窗口：2×2，stride=2

• 计算：

  O = 10 − 2 2 + 1 = 5 O = \frac{10 - 2}{2} + 1 = 5 O=210−2+1=5

• 输出：5×5×16

---

📌 C5 卷积层

• 输入：5×5×16

• 卷积核：120 个 5×5（全连接形式）

• 计算：

  O = 5 − 5 1 + 1 = 1 O = \frac{5 - 5}{1} + 1 = 1 O=15−5+1=1

• 输出：1×1×120

---

📌 F6 全连接层

• 输入：120
• 输出：84

---

📌 输出层

• 输入：84
• 输出：10（分类类别：0~9）

---

关键设计点解析

1. C3 的部分连接

   • 并非所有 16 个卷积核都连接前一层的 6 个通道，而是选择部分组合，减少参数。
   • 这是因为早期计算能力有限，同时也有助于增加特征多样性。

2. S 层的带学习系数平均池化

   • 与现代的 MaxPool 不同，LeNet-5 的平均池化包含一个可训练的缩放系数 + 偏置。

   • 即：

     y = a ⋅ avg ( x ) + b y = a \cdot \text{avg}(x) + b y=a⋅avg(x)+b

3. 激活函数 tanh

   • LeNet-5 使用 tanh / sigmoid 激活，而不是现代 CNN 常用的 ReLU。
   • 这导致梯度可能更容易消失，但在小规模网络上问题不大。

---

PyTorch 实现 LeNet-5

import torch
import torch.nn as nn
import torch.nn.functional as F

class LeNet5(nn.Module):
    def __init__(self, num_classes=10):
        super(LeNet5, self).__init__()
        # C1: 卷积层 1
        self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0)
        # S2: 平均池化
        self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2)
        # C3: 卷积层 2
        self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0)
        # S4: 平均池化
        self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2)
        # C5: 卷积层 3
        self.conv3 = nn.Conv2d(16, 120, kernel_size=5, stride=1, padding=0)
        # F6: 全连接层
        self.fc1 = nn.Linear(120, 84)
        # 输出层
        self.fc2 = nn.Linear(84, num_classes)

    def forward(self, x):
        x = torch.tanh(self.conv1(x))   # C1
        x = self.pool1(x)               # S2
        x = torch.tanh(self.conv2(x))   # C3
        x = self.pool2(x)               # S4
        x = torch.tanh(self.conv3(x))   # C5
        x = x.view(x.size(0), -1)       # 展平
        x = torch.tanh(self.fc1(x))     # F6
        x = self.fc2(x)                 # 输出层
        return x

---

训练与评估

import torch.optim as optim
from torchvision import datasets, transforms

# 数据准备（MNIST）
transform = transforms.Compose([
    transforms.Pad(2),   # MNIST 28x28 → 32x32
    transforms.ToTensor()
])
train_dataset = datasets.MNIST(root="./data", train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root="./data", train=False, download=True, transform=transform)

train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1000, shuffle=False)

# 模型、优化器、损失函数
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = LeNet5().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()

# 训练
for epoch in range(5):
    model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()
    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")

# 测试
model.eval()
correct = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        output = model(data)
        pred = output.argmax(dim=1)
        correct += pred.eq(target).sum().item()

print("Test Accuracy: {:.2f}%".format(100. * correct / len(test_dataset)))

---

实验扩展

我们可以对比 原版 LeNet-5 与现代改进版：

模型版本	激活函数	池化方式	归一化	数据增强	测试准确率
原版 LeNet-5	tanh	AvgPool	无	无	~99.0%
改进版	ReLU	MaxPool	BatchNorm	随机旋转、平移	~99.3%

👉 结论：现代改进提升了训练收敛速度与泛化性能。

---

总结

• LeNet-5 开创了 卷积、池化、全连接 的网络结构范式。
• 逐层计算公式 能帮助我们直观理解输入输出维度的变化。
• 其思想（局部感受野、权值共享、下采样）成为后续 CNN 的基石。
• PyTorch 实现与 MNIST 训练能直观感受这一网络的简洁与高效。
• 现代改进（ReLU、MaxPool、BN、数据增强）进一步提升效果。

---

参考资料

1. Yann LeCun - LeNet-5 原始论文 (1998)
2. PyTorch 官方文档：https://pytorch.org/docs/stable/nn.html
3. 深度学习经典模型讲解 - CSDN 博客

---