算法——数学基础

1. 导引问题：整数求和

给定整数 n ，计算 1+2+3+⋯+n 的结果，需兼顾计算效率与数据准确性。

方法一：循环累加法

核心思路

通过定义 sum 变量存储累加结果，使用 for 循环执行 n 次累加操作，逐步将 1 到 n 的整数加入 sum 中。

• 步骤 1：初始化 sum = 0（用于存储最终结果）；
• 步骤 2：循环变量从 1 遍历到 n ，每次循环执行 sum = sum + i（i 为当前循环变量）；
• 步骤 3：循环结束后，sum 即为所求的和。

时间复杂度

循环执行 n 次，时间复杂度为 O (n )。当 n 较小时（如 n ≤105），该方法效率可接受；但当 n 极大（如 n≥108）时，循环次数过多，效率会显著下降。

代码示例

#include <stdio.h>
int main() {
    int n, sum = 0;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        sum += i;
    }
    printf("%d\n", sum);
    return 0;
}

方法二：高斯公式法

核心思路

利用等差数列求和公式 sum=2n (n +1)，直接通过一次计算得到结果，无需循环。

• 数学原理：1 到 n 是首项为 1、末项为 n 、项数为 n 的等差数列，等差数列求和公式为 "（首项 + 末项）× 项数 ÷ 2"，代入后即得 2n (n+1)。

时间复杂度

仅需一次乘法和一次除法运算，时间复杂度为 O (1)，无论 n 多大，计算效率均远高于循环累加法。

实现风险与解决方案

• 风险：整数溢出
  当 n 较大时（如 n >46340），n (n +1) 的结果会超过 32 位 int 的最大值（2^31−1=2147483647），导致计算结果错误。例如 n =46341 时，46341×46342=2147490222，已超出 32 位 int 范围，直接计算会出现溢出。
• 解决方案
  1. 使用 64 位整数类型 long long：long long 范围为 −2^63 到 2^63−1（约 ±9e18），可容纳极大的中间结果；
  2. 优化运算顺序：当 n 为偶数时，先计算 n ÷2 再乘 (n +1)；当 n 为奇数时，先计算 (n +1)÷2 再乘 n ，避免中间结果过大。例如 n=5（奇数），先算 (5+1)÷2=3，再乘 5 得 15，这样做可以减少中间值大小而且不会改变原本的公式和结果

代码示例

#include <stdio.h>
int main() {
    int n;
    scanf("%d", &n);
    long long sum;
    // 优化运算顺序，避免溢出
    if (n % 2 == 0) {
        sum = (n / 2) * (n + 1);
    } else {
        sum = n * ((n + 1) / 2);
    }
    printf("%lld\n", sum); // %lld 是 long long 类型的输入输出格式符
    return 0;
}

编程思维差异

• 数学解法仅需保证公式正确；
• 编程需额外考虑：数据类型范围（如 int 与 long long 的选择）、运算顺序对中间结果的影响、边界情况（如 n =0 或 n 极大时的处理），需培养对数据范围的敏感性，提前预判溢出风险。

2. 应用案例一：最小公倍数（LCM）

问题描述

给定两个正整数 A 和 B ，求它们的最小公倍数（即能同时被 A 和 B 整除的最小正整数）。

方法一：暴力枚举法

基础思路

从两个数中较大的数开始逐个枚举，找到第一个能同时被 A 和 B 整除的数，即为最小公倍数。

• 示例：求 10 和 14 的最小公倍数
  较大数为 14，依次枚举 14（14÷10=1 余 4，不能整除）、15（15÷10=1 余 5，15÷14=1 余 1，不能整除）、...、70（70÷10=7，70÷14=5，能整除），故最小公倍数为 70。

效率问题

当 A 和 B 为大数时（如 A =108，B=108+1），需枚举到 108×(108+1) 次，运算量极大，效率极低，实际应用中不可行。

改进思路

枚举较大数的倍数而非逐个数字：较大数的倍数天然能被其整除，只需判断是否能被较小数整除，减少枚举次数。

• 示例：求 10 和 14 的最小公倍数
  较大数为 14，枚举其倍数 14（14÷10 余 4，不行）、28（28÷10 余 8，不行）、42（42÷10 余 2，不行）、56（56÷10 余 6，不行）、70（70÷10 余 0，可行），仅需 5 次枚举，效率显著提升。

方法二：数学公式法（结合辗转相除法）

核心公式

最小公倍数与最大公约数（GCD，能同时整除 A 和 B 的最大正整数）的关系为：

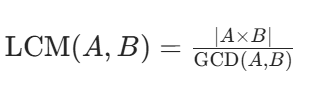
• 原理：A 和 B 的乘积等于它们的最小公倍数与最大公约数的乘积，因此通过最大公约数可直接计算最小公倍数。

关键：辗转相除法求 GCD

基本原理

求两个数的 GCD 等价于求 "较小数" 与 "两数相除余数" 的 GCD，重复此过程直到余数为 0，此时的 "较小数" 即为 GCD。

• 示例：求 10 和 14 的 GCD

1. 1. 14 ÷ 10 = 1 余 4 → 转为求 10 和 4 的 GCD；
   2. 10 ÷ 4 = 2 余 2 → 转为求 4 和 2 的 GCD；
   3. 4 ÷ 2 = 2 余 0 → 余数为 0，此时的 2 即为 GCD。

效率优势

无论 A 和 B 多大，辗转相除法的迭代次数均很少（如 A =109，B =109+1，仅需 2-3 步即可求出 GCD 为 1），时间复杂度为 O (log(min(A ,B)))，效率极高。

代码实现

int gcd(int da, int xiao) {
    int temp;
    while (xiao != 0) {
        temp = da % xiao;
        da = xiao;
        xiao = temp;
    }
    return da;
}

过程分析：

• 初始时，da = 14，xiao = 10。
• 第一次循环：temp = 14 % 10 = 4，然后 da = 10，xiao = 4。
• 第二次循环：temp = 10 % 4 = 2，然后 da = 4，xiao = 2。
• 第三次循环：temp = 4 % 2 = 0，然后 da = 2，xiao = 0。
• 此时 xiao = 0，循环结束，返回 da = 2，即 14 和 10 的最大公约数是 2。

思考：大小两个参数位置不能变？

如果交换 da 和 xiao 的位置（即传入的第一个参数比第二个小），算法仍然有效。因为在第一次循环计算余数后，da 和 xiao 的值会被更新，后续的计算会自动调整为用较大的数除以较小的数，不影响最终求最大公约数的结果。例如，计算 10 和 14 的最大公约数，过程如下：

• 初始 da = 10，xiao = 14。
• 第一次循环：temp = 10 % 14 = 10，然后 da = 14，xiao = 10，后续计算就和前面示例中计算 14 和 10 的最大公约数过程一致了，最终结果也是 2。

算法特点

• 容错性：即使输入时参数顺序错误（如先传小数再传大数），第一次迭代后会自动纠正（如输入 10 和 14 与 14 和 10，最终结果一致）；
• 无溢出风险：计算 LCM 时先执行 A ÷GCD，再乘 B ，避免 A ×B 直接计算导致的溢出（如 A =105，B =105，A ×B =1010 会溢出 32 位 int，但 A ÷GCD =105÷105=1，再乘 B 得 105，无溢出）。

3.应用案例二：n个n相乘个位数

题目描述：

给定一个正整数 N，请计算 N 个 N 相乘的结果的个位数是多少（1<=N<=1,000）。

解题思路：

方法一：暴力解法

暴力解法局限：直接计算会导致数值过大存储困难，当n=1000时结果已是天文数字

改进暴力法：每次乘法后只保留个位数，因为十位以上数字不影响最终结果的个位

• 示例：求 的个位数

2¹ 个位数 = 2；

2² 个位数 = (2×2) 个位数 = 4；

2³ 个位数 = (4×2) 个位数 = 8；

2⁴ 个位数 = (8×2) 个位数 = 16 -> 6；

2⁵ 个位数 = (6×2) 个位数 = 12 -> 2（与 2¹ 相同，开始循环）；

后续只需重复循环即可，无需计算完整的

• 时间复杂度：对于n=1000需要做999次乘法运算，时间复杂度为O(n)

方法二：数学规律

循环必然性：个位数字只有0-9十种可能，根据抽屉原理，最多11次运算后必然出现循环

找规律：

• 分析 N 从 1 到 10 时 的个位数情况：
  • 当 N = 1 时，1 ^ 1 = 1 ，个位数是 1 ；
  • 当 N = 2 时，2 ^ 2 = 4 ，个位数是 4 ；2 ^ 3 = 8 ，个位数是 8 ；2 ^ 4 = 16 ，个位数是 6；2 ^ 5 = 32 ，个位数是 2 ，开始循环，周期为 4 ；
  • 当 N = 3 时，3 ^ 1 = 3 ，3 ^ 2 = 9 ， 3 ^ 3 = 27 ，个位数是 7 ； 3 ^ 4 = 81 ，个位数是 1；3^5 = 243 ，个位数是 3 ，开始循环，周期为 4 ；
  • 当 N = 4 时，4 ^ 1 = 4 ，4 ^ 2 = 16 ，个位数是 6 ； 4 ^ 3 = 64 ，个位数是 4 ，周期为 2；
  • 当 N = 5 时，5 的任何正整数次幂个位数都是 5 ；
  • 当 N = 6 时，6 的任何正整数次幂个位数都是 6 ；
  • 当 N = 7 时，7 ^ 1 = 7 ，7 ^ 2 = 49 ， 7 ^ 3 = 343 ，个位数是 3 ； 7 ^ 4 = 2401 ，个位数是 1 ； 7 ^ 5 = 16807 ，个位数是 7 ，周期为 4 ；
  • 当 N = 8 时，8 ^ 1 = 8 ，8 ^ 2 = 64 ，个位数是 4 ； 8 ^ 3 = 512 ，个位数是 2 ； 8 ^ 4 = 4096 ，个位数是 6 ； 8 ^ 5 = 32768 ，个位数是 8 ，周期为 4 ；
  • 当 N = 9 时，9 ^ 1 = 9 ，9 ^ 2 = 81 ，个位数是 1 ； 9 ^ 3 = 729 ，个位数是 9 ，周期为 2 ；
  • 当 N = 10 时，10 的任何正整数次幂个位数都是 0 ；
• 对于任意的 N ，先看 N 的个位数，根据上述规律来确定 的个位数；
  • N = 26 ，只看个位数 6 ，6 的任何正整数次幂个位数都是 6 。

具体分析操作：

求：当n = 13时，的个位数结果

1. 根据刚才的暴力解法，取个位数再乘以下一个数 = 13 -> 3
2. 根据3 的幂次个位数规律来计算

通过刚刚上面的分析

当 N = 3 时，3 ^ 1 = 3 ，3 ^ 2 = 9 ， 3 ^ 3 = 27 ，个位数是 7 ； 3 ^ 4 = 81 ，个位数是 1 ；3^5 = 243 ，个位数是 3 ，开始循环，周期为 4 ；

3的幂次的周期为4

所以13÷4=3⋯⋯1，其中余数是 1

这意味着 的个位数和周期中第 1 个位置的数相同，也就是 3

4. 应用案例三：Fibonacci 数列除 3 的余数判断

问题描述：

有一种 fibonacci 数列，定义如下：F(0) = 7，F(1) = 11，F(n) = F(n - 1) + F(n - 2) (n>=2)

给定一个 n (n < 1,000,000)，请判断 F(n) 能否被3整除，分别输出 yes 和 no ；

解法：

方法一：递归

但是能不用递归就不用，有超时和报栈的风险；

方法二：找规律

F(n) % 3 = (F(n - 1) + F(n - 2)) % 3 = (F(n - 1) % 3 + F(n - 2) % 3) % 3，即每一项对 3 取余，都是前两项对 3 取余的和对 3 取余；

当 n = 0 时，F(0) % 3 = 7 % 3 = 1；

当 n = 1 时，F(1) % 3 = 11 % 3 = 2；

当 n = 2 时，F(2) % 3 = (F(2 - 1) + F(2 - 2)) % 3 = (F(2 - 1) % 3 + F(2 - 2) % 3) % 3 = (11 % 3 + 7 % 3) % 3 = 0；

当 n = 3 时，F(3) % 3 = (F(3 - 1) % 3 + F(3 - 2) % 3) % 3 = (0 + 2) % 3 = 2；

当 n = 4 时，F(4) % 3 = (F(4 - 1) % 3 + F(4 - 2) % 3) % 3 = (2 + 0) % 3 = 2；

当 n = 5 时，F(5) % 3 = (F(5 - 1) % 3 + F(5 - 2) % 3) % 3 = (2 + 2) % 3 = 1；

当 n = 6 时，F(6) % 3 = (F(6 - 1) % 3 + F(6 - 2) % 3) % 3 = (1 + 2) % 3 = 0；

当 n = 7 时，F(7) % 3 = (F(7 - 1) % 3 + F(7 - 2) % 3) % 3 = (0 + 1) % 3 = 1；

当 n = 8 时，F(8) % 3 = (F(8 - 1) % 3 + F(8 - 2) % 3) % 3 = (1 + 0) % 3 = 1；

当 n = 9 时，F(9) % 3 = (F(9 - 1) % 3 + F(9 - 2) % 3) % 3 = (1 + 1) % 3 = 2；

当 n = 10 时，F(10) % 3 = (F(10 - 1) % 3 + F(10 - 2) % 3) % 3 = (2 + 1) % 3 = 0；

......

周期为8；

具体操作分析：

计算F(13) 是否能够整除

就只要看13除以8的余数对应的规律，13÷8=1 ...... 5，对应过去规律

当 n = 5 时，F(5) % 3 = (F(5 - 1) % 3 + F(5 - 2) % 3) % 3 = (2 + 2) % 3 = 1；

结果是1，所以不能整除

5.应用案例四：快速幂运算

问题描述：

要求计算 的最后三位数

方法一：暴力解法

直接循环计算 a ×a ×⋯×a （共 b 次），每次乘法后取模 1000。

• 示例：计算 23的126次方1000，循环 126 次，每次乘 23 后取模。
• 时间复杂度：O (b )，与指数 b 成正比。
• 局限性：当 b 极大（如 109）时，暴力法效率极低，无法在合理时间内完成。

方法二：快速幂算法

原理：利用指数二分 思想，将 ab 拆解为更小的幂次组合，减少乘法次数。例如：

• a 8=(a 4)2=[(a2)2]2，只需 3 次乘法（而暴力法需 7 次）。
• 核心公式：

• • 若 b 为偶数：

    

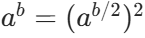
  • 若 b 为奇数：

    

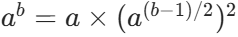
递归实现

int fastPowRecursive(int a, int b, int mod) {
    if (b == 0) return 1; // 指数为0，返回1（任何数的0次幂为1）
    int half = fastPowRecursive(a, b / 2, mod); // 计算a^(b/2)
    int result = (half * half) % mod; // 先算平方
    if (b % 2 == 1) { // 若指数为奇数，再乘一次a
        result = (result * a) % mod;
    }
    return result;
}

• 时间复杂度：O (logb)，因为每次递归指数减半。

非递归实现（更高效）

int fastPowIterative(int a, int b, int mod) {
    int ans = 1; // 初始化为1，因为1乘任何数不改变结果
    a = a % mod; // 先对底数取模，减少后续计算量
    while (b > 0) {
        if (b % 2 == 1) { // 若当前指数位为奇数，乘入结果
            ans = (ans * a) % mod;
        }
        a = (a * a) % mod; // 底数平方
        b = b / 2; // 指数二分
    }
    return ans;
}

• 执行过程（以 212mod1000 为例）：

• • 初始：ans =1，a =2，b=12
  • 第一次循环：b 为偶数，ans=1，a =2^2=4，b=6
  • 第二次循环：b 为偶数，ans=1，a =4^2=16，b=3 -> 16^3 -> 1 * 16 * (16^2)^1
  • 第三次循环：b 为奇数，ans =1*16 = 16；a =16^2=256，b=1 -> 16 * 256 * (256^2)^0
  • 第四次循环：b 为奇数，ans =16×256=4096, a =256^2=65536，，b=0
  • 结果16×256=4096 mod 1000=96；
  • 最终返回 96。

• 优势：无递归栈溢出风险，效率更高，时间复杂度仍为 O (logb)。

注意事项

1. 取模时机 ：每次乘法（包括底数平方、结果累乘）后立即取模，防止数值溢出（如 a 或 an s 超过整型范围）。
2. 初始值设置 ：ans 必须初始化为 1（因为任何数的 0 次幂为 1，且乘法单位元是 1）。
3. 奇数处理：循环中需判断指数是否为奇数，若为奇数则将当前底数乘入结果。
4. 算法选择 ：非递归实现更推荐，尤其当 b 极大时，避免递归栈溢出。

6.应用案例五：二分查找

基本概念

二分查找（Binary Search）是一种高效的查找算法，它通过反复将查找范围减半来定位目标值，仅适用于有序排列的数据（通常是升序或降序数组）。

适用条件

• 数据必须是有序的（如递增数列：2, 3, 4, 5, 6, 8, 12, 20, 32, 45, 65, 74, 86, 95, 100）
• 数据支持随机访问（如数组，可通过下标直接访问元素）

与顺序查找的对比

• 顺序查找 ：从第一个元素逐个向后比较，平均比较次数为 n /2 次，时间复杂度 O (n)
• 二分查找 ：每次缩小一半范围，时间复杂度 O (logn)
• 效率差异：当 时，顺序查找平均需 50 万次比较，而二分查找最多仅需 20 次（）

核心思想

通过每次与中间元素比较，将查找范围缩小一半：

• 若目标值等于中间元素，查找成功
• 若目标值大于中间元素，在右半部分继续查找
• 若目标值小于中间元素，在左半部分继续查找

算法实现

题目描述

给定升序数组 [2, 3, 4, 5, 6, 8, 12, 20, 32, 45, 65, 74, 86, 95, 100]，查找目标值 25 的位置。

查找过程演示

1. 初始范围：left=0（首元素下标），right=14（尾元素下标）
2. 第一次查找：

• • 计算中间位置：mid = (0+14)/2 = 7
  • 中间元素：a [7] = 20
  • 比较：25 > 20 → 目标在右半部分，调整 left=mid+1=8

1. 第二次查找：

• • 新范围：left=8，right=14
  • 中间位置：mid=(8+14)/2=11
  • 中间元素：a [11] = 74
  • 比较：25 < 74 → 目标在左半部分，调整 right=mid-1=10

1. 第三次查找：

• • 新范围：left=8，right=10
  • 中间位置：mid=(8+10)/2=9
  • 中间元素：a [9] = 45
  • 比较：25 < 45 → 目标在左半部分，调整 right=mid-1=8

1. 第四次查找：

• • 新范围：left=8，right=8
  • 中间位置：mid=8
  • 中间元素：a [8] = 32
  • 比较：25 < 32 → 目标在左半部分，调整 right=mid-1=7

1. 终止条件：left=8 > right=7 → 查找失败，目标值不存在

非递归实现（C 语言）

#include <stdio.h>

// 二分查找非递归实现
// 参数：arr-有序数组，n-数组长度，target-目标值
// 返回：找到返回下标，未找到返回-1
int binarySearch(int arr[], int n, int target) {
    int left = 0;          // 左边界初始化为0
    int right = n - 1;     // 右边界初始化为数组最后一个元素下标
    
    // 循环条件：left <= right（包含等于，确保最后一个元素被检查）
    while (left <= right) {
        int mid = left + (right - left) / 2;  // 避免(left+right)可能的溢出
        
        if (arr[mid] == target) {
            return mid;  // 找到目标，返回下标
        } else if (arr[mid] < target) {
            left = mid + 1;  // 目标在右半部分，调整左边界
        } else {
            right = mid - 1;  // 目标在左半部分，调整右边界
        }
    }
    return -1;  // 循环结束仍未找到，返回-1
}

int main() {
    int arr[] = {2, 3, 4, 5, 6, 8, 12, 20, 32, 45, 65, 74, 86, 95, 100};
    int n = sizeof(arr) / sizeof(arr[0]);
    int target = 25;
    
    int result = binarySearch(arr, n, target);
    if (result != -1) {
        printf("目标值 %d 位于下标 %d\n", target, result);
    } else {
        printf("目标值 %d 不存在于数组中\n", target);
    }
    return 0;
}

递归实现（C 语言）

#include <stdio.h>

// 二分查找递归实现
// 参数：arr-有序数组，left-左边界，right-右边界，target-目标值
// 返回：找到返回下标，未找到返回-1
int binarySearchRecursive(int arr[], int left, int right, int target) {
    // 递归出口：左边界大于右边界，查找失败
    if (left > right) {
        return -1;
    }
    
    int mid = left + (right - left) / 2;  // 计算中间位置
    
    if (arr[mid] == target) {
        return mid;  // 找到目标，返回下标
    } else if (arr[mid] < target) {
        // 目标在右半部分，递归查找右半区间
        return binarySearchRecursive(arr, mid + 1, right, target);
    } else {
        // 目标在左半部分，递归查找左半区间
        return binarySearchRecursive(arr, left, mid - 1, target);
    }
}

int main() {
    int arr[] = {2, 3, 4, 5, 6, 8, 12, 20, 32, 45, 65, 74, 86, 95, 100};
    int n = sizeof(arr) / sizeof(arr[0]);
    int target = 32;
    
    int result = binarySearchRecursive(arr, 0, n - 1, target);
    if (result != -1) {
        printf("目标值 %d 位于下标 %d\n", target, result);
    } else {
        printf("目标值 %d 不存在于数组中\n", target);
    }
    return 0;
}

递归与非递归对比

|----------|-------------|----------|-------------------|
| 实现方式 | 优点 | 缺点 | 空间复杂度 |
| 非递归 | 效率高，无栈溢出风险 | 逻辑稍复杂 | O(1) |
| 递归 | 代码简洁，体现分治思想 | 深度过大会栈溢出 | O (logn)（递归栈） |

时间复杂度

• 每次查找将范围缩小一半，最多需要 log2n+1 次比较
• 时间复杂度：O (logn)
• 实例：100 万数据（220≈106）最多需要 20 次比较

空间复杂度

• 非递归实现：仅使用常数个变量，空间复杂度 O(1)
• 递归实现：递归调用深度为 logn ，空间复杂度 O (logn)

适用场景

• 大规模有序数据的查找（如字典查询、数据库索引查询）
• 不经常变动的静态数据（因为插入删除会破坏有序性）

注意事项

1. 必须保证数据有序，无序数据需先排序（排序成本 O (n logn)）
2. 处理重复元素时，二分查找只能返回其中一个位置，如需找到第一个 / 最后一个出现位置，需额外处理
3. 对频繁插入删除的动态数据，二分查找效率不高（维护有序性成本高）
4. 小数据量场景下，顺序查找可能更高效（避免二分查找的额外逻辑开销）

7.应用案例六：二分查找的应用

题目描述

给定方程 f (x )=x 3+5x 2+3x +1，已知 Y 满足 f (0)≤Y ≤f (100)，要求在区间 [0,100] 内求解 f (x )=Y 的解，结果精确到小数点后 4 位。

核心前提：单调性证明

要使用二分法求解连续函数方程，需满足函数在区间内单调且连续 。

对本题方程 f (x )=x 3+5x 2+3x+1 分析：

• 连续性：多项式函数在全体实数域内连续，[0,100] 属于定义域，满足连续性；
• 单调性：求导得 f ′(x )=3x 2+10x +3，在区间 [0,100] 内，x ≥0，因此 3x 2≥0、10x ≥0、常数项 3>0，即 f ′(x )>0，函数在 [0,100] 内严格单调递增 。
  单调性意味着：若 x 1<x 2，则 f (x 1)<f (x 2)，方程 f (x )=Y 在区间内有且仅有一个解，符合二分法适用条件。

核心逻辑

类比离散数组的二分查找：将连续区间 [l e f t ,r i g h t ] 不断减半，通过比较区间中点的函数值与目标值 Y 的大小，缩小解的范围，直到区间长度小于预设精度（满足题目要求的小数点后 4 位）。

具体步骤（以 Y=1000 为例）

1. 初始化区间 ：设左边界 l e f t =0，右边界 r i g h t=100（题目给定区间）；
2. 边界检查 ：先计算 f (0)=0^3+5×0^2+3×0+1=1，f(100)=100^3+5×100^2+3×100+1=1050301，验证 1≤1000≤1050301，确认解存在；
3. 二分迭代：

• • 第 1 次迭代：计算中点 mid =(0+100)/2=50，求 f (50)=50^3+5×50^2+3×50+1=125000+12500+150+1=137651。由于 137651>1000，说明解在左半区间，更新 right=50；
  • 第 2 次迭代：中点 mid =(0+50)/2=25，f (25)=25^3+5×25^2+3×25+1=15625+3125+75+1=18826>1000，更新 right=25；
  • 第 3 次迭代：中点 mid =(0+25)/2=12.5，f (12.5)=12.5^3+5×12.5^2+3×12.5+1=1953.125+781.25+37.5+1=2772.875>1000，更新 right=12.5；
  • 第 4 次迭代：中点 mid =(0+12.5)/2=6.25，f (6.25)=6.25^3+5×6.25^2+3×6.25+1=244.140625+195.3125+18.75+1=459.203125<1000，说明解在右半区间，更新 left=6.25；
  • 重复上述过程，直到 r i g h t −l e f t<10−6（预设精度高于题目要求的 10−4，避免四舍五入误差）；

1. 结果输出 ：当区间满足精度要求时，取 mi d =(l e f t +r i g h t)/2 作为解，保留小数点后 4 位。

代码实现（C++）

#include <bits/stdc++.h> // 万能头文件，包含常用库
using namespace std;

// 定义目标函数 f(x) = x³ + 5x² + 3x + 1
double f(double x) {
    return x * x * x + 5 * x * x + 3 * x + 1;
}

// 二分法求解方程 f(x) = Y 在 [0, 100] 内的解
double binarySearchForEquation(double Y) {
    double left = 0.0, right = 100.0;
    // 边界检查：确认解存在
    if (f(left) > Y || f(right) < Y) {
        cout << "在区间 [0, 100] 内无解！" << endl;
        return -1.0; // 返回无效值标识错误
    }
    // 迭代终止条件：区间长度小于 1e-6，确保结果精确到小数点后 4 位
    while (right - left > 1e-6) {
        double mid = left + (right - left) / 2; // 避免 (left+right) 溢出（虽此处为double，仍保持规范）
        double f_mid = f(mid);
        if (f_mid == Y) {
            return mid; // 恰好找到解，直接返回
        } else if (f_mid < Y) {
            left = mid; // 解在右半区间，更新左边界
        } else {
            right = mid; // 解在左半区间，更新右边界
        }
    }
    // 区间满足精度，返回中点作为最终解
    return (left + right) / 2;
}

int main() {
    double Y;
    cout << "请输入 Y 的值（需满足 f(0) ≤ Y ≤ f(100)）：";
    cin >> Y;
    
    double solution = binarySearchForEquation(Y);
    if (solution != -1.0) {
        cout << fixed << setprecision(4); // 设置输出精度为小数点后 4 位
        cout << "方程 f(x) = " << Y << " 的解为：x = " << solution << endl;
    }
    return 0;
}

8.应用场景七：函数最小值求解

题目描述

给定函数 f (x )=x 3−6x 2+9x+2，要求在区间 [0,5] 内求函数的最小值，结果精确到小数点后 4 位。

核心分析：函数单调性与极值点

• 直接判断单调性：计算特殊点函数值，f (0)=2，f (1)=1−6+9+2=6，f (2)=8−24+18+2=4，f (3)=27−54+27+2=2，f(4)=64−96+36+2=6，可见函数在 [0,5] 内先减后增，不满足整体单调性，无法直接用二分法求最小值，需转化问题。
• 导数分析：求导得 f ′(x )=3x 2−12x +9=3(x −1)(x−3)。导数的符号决定函数单调性：

• • 当 x <1 时，f ′(x)>0，函数单调递增；
  • 当 1<x <3 时，f ′(x)<0，函数单调递减；
  • 当 x >3 时，f ′(x)>0，函数单调递增；
  • 导数为 0 的点（x =1、x =3）是极值点，其中 x=3 处函数取得最小值（因左侧递减、右侧递增）。

转化思路：将 "求最小值" 转化为 "求导数零点"

函数最小值出现在导数由负变正的零点处（即 f ′(x )=0 且左侧 f ′(x )<0、右侧 f ′(x )>0）。由于本题导数 f ′(x )=3x 2−12x +9 是二次函数，在区间 [1,3] 内单调递减 （二次函数开口向上，对称轴为 x =2，[1,3] 内先减后增？此处修正为：在区间 [2,5] 内导数单调递增，因对称轴 x=2，右侧导数随 x 增大而增大），满足单调性，可对导数函数用二分法求零点，该零点即为原函数的最小值点。

具体步骤

1. 确定导数函数与目标区间 ：设导数函数 g (x )=f ′(x )=3x 2−12x +9，目标区间为 [2,4]（因 g (2)=12−24+9=−3<0，g(4)=48−48+9=9>0，导数在该区间内由负变正，存在零点）；
2. 二分迭代求导数零点 ：
   • 第 1 次迭代：中点 mi d =(2+4)/2=3，g (3)=27−36+9=0，恰好找到零点，即 x=3 是导数零点；
   • 若未直接找到，继续迭代：若 g (mi d )<0，说明零点在右半区间（l e f t =mi d ）；若 g (mi d )>0，说明零点在左半区间（r i g h t =mi d ），直到区间长度小于 1e−6；
3. 求最小值 ：将导数零点代入原函数 f (x)，得到最小值。

代码实现（C++）

#include <bits/stdc++.h>
using namespace std;

// 原函数 f(x) = x³ - 6x² + 9x + 2
double f(double x) {
    return x * x * x - 6 * x * x + 9 * x + 2;
}

// 导数函数 g(x) = f'(x) = 3x² - 12x + 9
double g(double x) {
    return 3 * x * x - 12 * x + 9;
}

// 二分法求导数 g(x) = 0 在 [a, b] 内的零点（即原函数的最小值点）
double findMinPoint(double a, double b) {
    double left = a, right = b;
    // 验证区间内导数是否由负变正（确保存在最小值点）
    if (g(left) >= 0 || g(right) <= 0) {
        cout << "该区间内无最小值点（导数未由负变正）！" << endl;
        return -1.0;
    }
    // 迭代终止条件：区间精度 1e-6
    while (right - left > 1e-6) {
        double mid = left + (right - left) / 2;
        double g_mid = g(mid);
        if (g_mid == 0) {
            return mid; // 找到精确零点
        } else if (g_mid < 0) {
            left = mid; // 零点在右半区间
        } else {
            right = mid; // 零点在左半区间
        }
    }
    return (left + right) / 2; // 返回近似零点
}

int main() {
    double min_point = findMinPoint(2.0, 4.0); // 导数由负变正的区间
    if (min_point != -1.0) {
        double min_value = f(min_point);
        cout << fixed << setprecision(4);
        cout << "函数在区间 [0,5] 内的最小值点为：x = " << min_point << endl;
        cout << "对应的最小值为：f(x) = " << min_value << endl;
    }
    return 0;
}

导数应用的核心逻辑

• 若函数可导，其极值点必在导数为 0 或导数不存在的点处；
• 若导数在区间内单调，则导数零点唯一，可通过二分法快速定位；
• 对于不可导的函数（如分段函数），需结合函数单调性直接分析极值点，或使用 "三分查找"（后续章节内容）。

与三分查找的对比

|----------|-------------------|------------|-------------------------|
| 方法 | 适用场景 | 核心条件 | 效率 |
| 导数 + 二分法 | 可导函数，且导数单调 | 函数可导、导数单调性 | O (log(ϵ R −L)) |
| 三分查找 | 单峰函数（先增后减 / 先减后增） | 函数具有凸性 | |

9.应用案例八：三分查找

三分查找的概念与背景

适用场景：用于求解单峰函数的极值问题（最大值或最小值）

基本思想：通过比较区间内两个三等分点的函数值，逐步缩小极值点所在区间

关键公式：

• 左三等分点：LeftThird=(Left×2+Right)/3
• 右三等分点：RightThird=(Left+Right×2)/3
• 三分查找的步骤
  • 具体流程：
    • 计算当前区间的左、右三等分点
    • 根据比较结果缩小搜索区间：
    • 比较两个三等分点的函数值
      • 对于上凸函数（寻找最大值）：
        • 若f(LeftThird) > f(RightThird)，则极值点在左半区
        • 否则极值点在右半区
      • 对于下凸函数（寻找最小值）则相反
    • 重复上述过程直到区间足够小

三分查找与二分查找的区别

• 前提条件：

• • 二分查找：要求数据单调
  • 三分查找：要求数据具有凸性（单峰性）

• 比较对象：

• • 二分查找：比较目标值与中间值
  • 三分查找：比较两个三等分点的函数值

• 应用场景：

• • 二分查找：查找特定值
  • 三分查找：查找极值点

三分查找的递归与非递归实现

• 实现方式：
  • 递归实现：通过函数递归调用实现区间缩小
  • 非递归实现：通过循环和变量更新实现
• 编程要点：
  • 终止条件：区间长度小于指定精度
  • 每次迭代可将搜索范围缩小约1/3

三分查找的应用条件

• 凸性要求：
  • 函数在区间内是单峰的（只有一个极值点）
  • 不要求函数可导，分段函数也可使用
  • 可导时表现为导数单调递增或递减
• 验证方法：
  • 观察函数图像形状
  • 分析导数变化趋势