神经网络介绍
神经网络是一类仿生学算法,其由若干类神经处理单元组成:
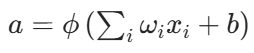
就是在一个感知机当中加入了激活函数的成分,而感知机则在笔者之前的博客有涉及:感知机相关文章
这里的w_i表示权重,x_i为输入,而b则是偏置
而多层感知机即可组成最简单的前向神经网络,如图:
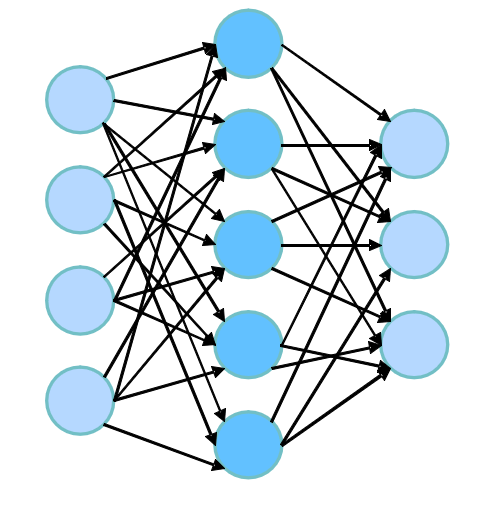
最前面的叫输入层,其次是隐藏层和输出层(这里省去了偏置),其中隐藏层在一般情况下都不止一层
计算图的表示方案
神经网络在计算机内部的表示往往只需要依靠节点 和边来实现
其中:
节点表示创建输入张量、矩阵、向量的函数
边表示节点产生和输入的变量,即张量、矩阵、向量
这里举一个简单的例子:
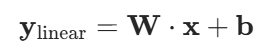
我们来表示上面的线性变换表达式,并设激活函数为ReLU,得到的计算图为:
+-----------------+
| |
| Input (x) |
| [x1, x2]^T |
| |
+--------+--------+
|
| (边:传递 x)
v
+-----------------+
| |
| Linear (Wx+b) |
| 计算 y_linear |
| |
+--------+--------+
|
| (边:传递 y_linear)
v
+-----------------+
| |
| ReLU |
| 计算 y_relu |
| |
+-----------------+之所以需要画计算图主要是为了更好的完成神经网络前向传播计算和神经网络反向传播计算:
前向和反向传播算法
传播算法的主要目的是在实现网络架构之后能够实现参数估计,最常见的参数估计主要由MAP和MLE实现,这里我们不做讨论
根据前文,我们将神经网络的计算过程表示为计算图 ,节点v_1, v_2, ..., v_N满足拓扑排序,通过其关联性,推算出各个节点对于输出的导数
反向传播具体流程
反向传播通过 "前向传播" 和 "反向传播" 两步完成导数计算:
前向传播(Forward Pass)
按拓扑排序顺序i从1到N,依次计算每个节点v_i的值 ------ 计算方式为 "基于其父节点Pa(v_i)的值" 进行函数运算。
反向传播(Backward Pass)
从计算图的最后一个节点v_N开始,然后从(i=N-1)到1逆序遍历节点,利用链式法则计算每个节点的导数:
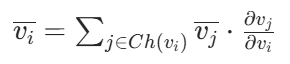
具体例子
还是沿用上面那个简单的例子,我们来研究一下如何运用反向传播法实现相关计算:
参数定义
首先,我们先明确一下各个参数的定义:
输入:
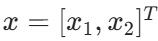
线性层参数------权重矩阵:
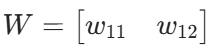
线性层输出:

ReLU 层输出:
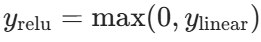
假设最终损失为 L,我们需要计算:
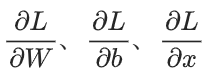
前向传播
按拓扑顺序(输入 → 线性层 → ReLU 层)计算:
- 输入层:x_1、x_2
- 线性层:
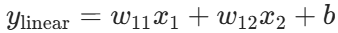
- ReLU 层:
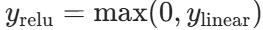
反向传播
假设 y_relu 是损失 L 的直接输入,我们这里设损失函数:
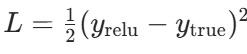
则ReLU梯度为:
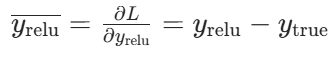
线性层的梯度为:
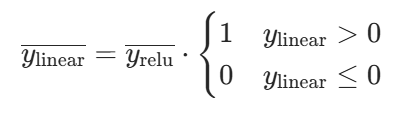
参数 W、b 和输入 x 的梯度为:
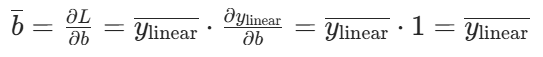
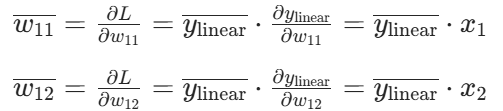
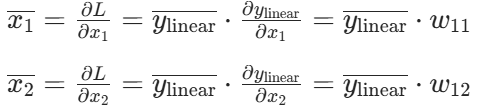
梯度爆炸或消散
根据前文反向传播法计算得出的规律:
将 "损失对第一层权W1的梯度" 推广到含k层隐藏层的神经网络,得到梯度的一般形式:
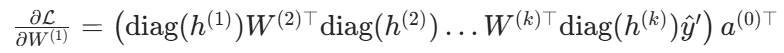
其中:
- a为输入层
- w为各层权重
- diag为激活函数在h处的导数的对角矩阵
为分析梯度随层数的变化,引入两个关键量:
β:激活函数导数对角矩阵diag的最大奇异值
γ:权重矩阵W的最大奇异值
根据矩阵范数不等式,梯度的范数满足:
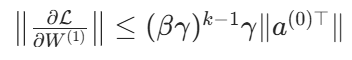
由此得出核心规律:
若βγ > 1:随着隐藏层层数k增加,梯度会指数级增长 ,引发梯度爆炸(参数更新幅度过大,训练极不稳定)
若βγ < 1:随着k增加,梯度会指数级衰减 ,引发梯度消散(底层参数几乎无法更新,深层网络难以训练)
为了让梯度稳定传递,我们往往会选择更加合适的激活函数、权重初始值和网络架构