【 C/C++ 算法】入门动态规划-----一维动态规划基础（以练代学式）

每日激励："不设限和自我肯定的心态：I can do all things。 --- Stephen Curry"
**绪论​：
本章是动态规划算法的基础入门篇，我将通过三道简单题 + 一道中等难度的一维动态规划题来带你对动态规划有个初认识，并基本了解动态规划的最基本常见的写法，只有将基本写法了解了，对后续的难的题目自然也不会毫无头绪，后续还将持续更新更多相关的动规算法，敬请期待~🙃

早关注不迷路，话不多说安全带系好，发车啦（建议电脑观看）。**

---

👻动态规划🌥️

这里通过大量练习得出下面动态规划做题步骤

简单的说动态规划理解成：某种状态的公式 + 提前求出来值的容器 求出当前位置的值 然后放到容器中后后续使用

因为最开始的值一般是会看见的所以就能有初始值，从而启动动态规划

从上中可以主要提炼出：

• 状态
• 容器的重要性
• 公式，可以换种说法：状态转移方程

这样严格😈的说：动态规划 = 状态定义 + 状态转移方程 + 初始条件 + 状态存储（容器）

---

下述步骤是通过写完下述四道题后的总结，所以同样需要道友🗡️大量的练习沉淀最终就能对动态规划的题目有一个基本的了解和思路，同时建议这里先一眼看过在做题中不断的磨炼同时再看这里，慢慢的找感觉。

---

动规基本步骤

1. 状态表示 ：就是dp表（容器一般是数组）中里面的dp[ i ]值的含义
   1. 通过经验 + 题目要求：通常为：以 i 位置结尾，xxxxx
   2. 分析问题的过程中，发现相同的子问题
2. 状态转移方程 ：本质就是 dp[ i ] = ?（也是最难的一步）
   1. 通过状态表示 再结合 题目含义推导处dp[ i ]的值到底为多少
3. 初始化 ：
   1. 保证填表的时候不越界
   2. 主要也是根据题目进行
4. 填表顺序 ：
   1. 为了保证填写当前状态的时候前面状态已经存到容器中，这样才能进行计算
   2. 一般是从左向右/从上到下
5. 返回值
   1. 通过最终得到的dp表和题意找到dp表中的结果

附⭐⭐⭐：

1. 状态表示：通常为：以 i 位置结尾/开头，xxxxx
2. dp[ i ] 通常通过最后一个状态来进行分析
3. 初始化 通常通过第一个状态来进行分析
4. 再做类似数字判断时，不要使用字符来简单的判断，而是将数字字符根据位数转变为真正的数字然后再进行判断，不要偷懒会容易出现不可控的情况（具体见题目4）
5. 适当的需要的情况下可以开辟空间来处理边界问题，这点在后面稍微进阶一点的动规来说就是使用的更多

---

🥴话不多说，从题目来以练代学式的快速上手，我也会边分析过程边使用上述的5步骤

---

具体训练：

1. 第 N 个泰波那契数🤓

题目🍪：

分析题目并提出，解决方法📕：

回顾五大步骤：

1. 状态表示：就是dp表中里面的值的含义

怎么来：

1. 经验 + 题目要求
2. 分析问题的过程中，发现子问题

2. 状态转移方程：本质就是dp[ i ] 等于什么（也是最难的一步）
   1. 根据状态表示 + 题目含义得出
3. 初始化
   1. 保证填表的时候不越界
   2. 也是根据题目意思进行填写
4. 填表顺序
   1. 为了填写当前状态的时候，所需要的状态已经计算过了
   2. 一般是从左向右/从上到下
5. 返回值
   1. 题目要求 + 状态表示

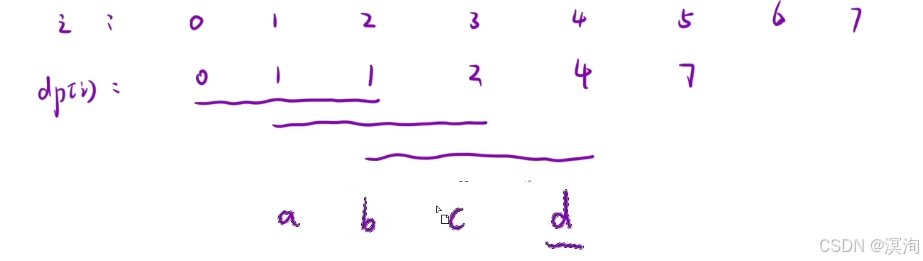
题解核心逻辑✍️：

1. 状态表述：dp[ i ]：第 i 个泰波那契数
   1. 根据经验 + 题目要求
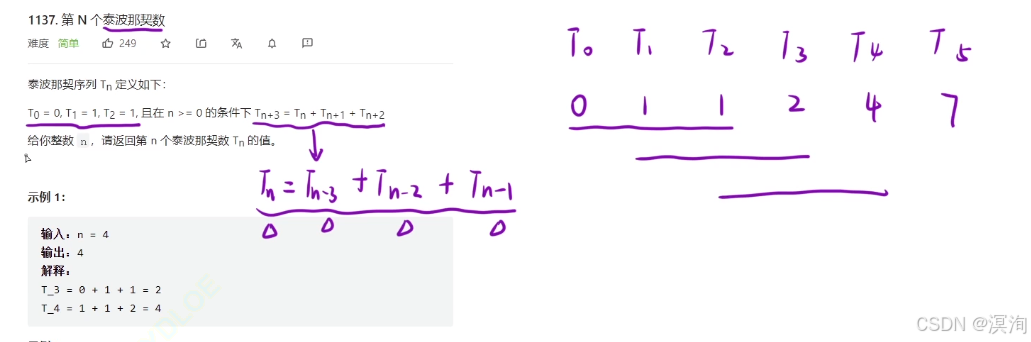
2. 本题的转移方程： dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]（通过上图总的公式直接得出）
3. 初始化，对本题的 dp[0]、dp[1]、dp[2] 这三个位置初始化，才能进行正常的开始
   
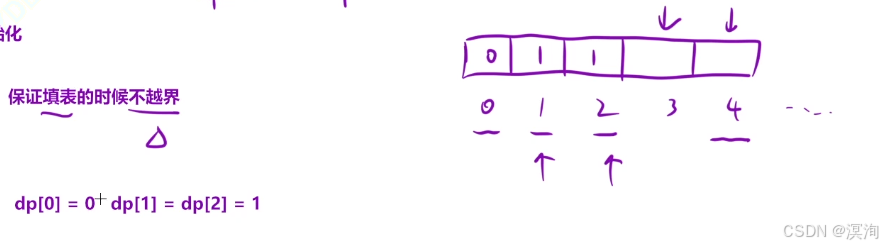
4. 填表顺序
   1. 需要在求第 i 位置那么： i - 1、i - i、i -3 三个位置的值都得算好
   2. 所以需要：从左向右
      
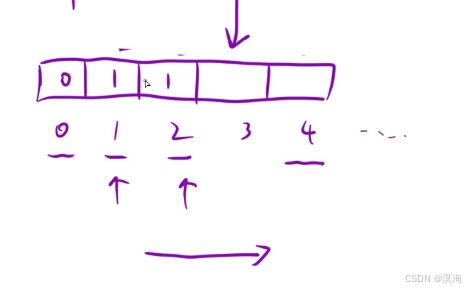
5. 返回值
   1. 题目要求：第 n 个的值 dp[ n ]即可
6. 空间优化：当我们在填某个表，某个状态只需要前面的若干个状态时，就可以使用滚动数组进行优化，本题仅需要某个数的前3个即可
   1. 本题仅需要3个变量abc来标明前3个数，求d的数
   2. 通过移动 abcd 四个数，来代替dp表
      

源码🗒️

class Solution {
public:
		int tribonacci(int n) {
        //1. 状态表示：dp[i] = 第i个泰波那契序列
        //2. 状态表示：Tn+3 = Tn + Tn+1 + Tn+2 -> dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
        vector<int> dp(n + 1);//提前开辟好 n 个位置的空间，注意从0开始所以+1
        //3. 初始化：需要前三个 那么就是初始化 0 1 2，从3开始
        dp[0] = 0,dp[1] = 1,dp[2] = 1;
        //4. 填表顺序：要求的值是Ti，那么求就是 dp[i]，所以肯定是从小的开始，也就是从左往右
        for(int i = 3;i <= n;i++)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];//这里本质就是使用状态转移方程
        }
        //5. 返回值：dp[i]即可
        return dp[n];
    }

    int tribonacci(int n) {
    //空间优化写法：
        int a = 0,b = 1,c = 1;
        int ret = 0;
        if(n == 0) return 0; 
        if(n == 1 || n == 2) return 1; 
        for(int i = 3 ; i <= n;i++){//填表顺序
            ret = a + b + c;
            a = b;b = c;c = ret;
        }
        return ret;
    }
};

2. 三步🚶问题

题目👻：

分析题目并提出，解决方法🫏：

这里主要理解成：

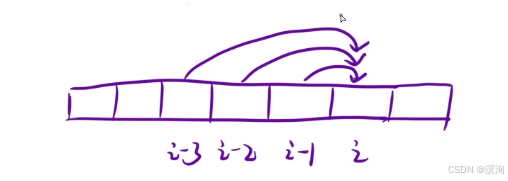
• 本题分析不难看出：要求到达某个台阶的方法（这里就能简单的看出来状态表示）
• 直接拿示例一来看：如何到达台阶n=3：
  1. 也很简单：因为小孩每次可以走1/2/3步，那么那几个阶能到达呢？
  2. 无非就是 n - 1、n - 2 、n - 3 （这里n=3，故从0 1 2阶能到达这里就能看出来状态转移方程： dp[n] = dp[n-1] + dp[n-2] + dp[n-3]）
  3. 那么要初始化的就是 dp[0]、dp[1]、dp[2]
  4. 从状态表示也能很简单的推出，因为本质阶梯不高：
     1. dp[0]：走到0，那么就是不用走也就是走0步，故为1
     2. dp[1]：走到1，只能从0走一步，故也为1
     3. dp[2]：走到2，那么就能从0走2步和从1走1步，所以为2
  5. 剩下就是移动方向：自然和上题一样从左往右、返回dp[n]即可

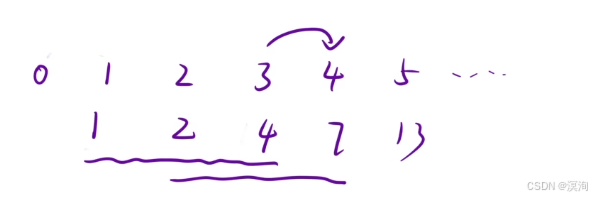
再拿走到4来看：

• 向下的 1 2 3 个台阶，如能到达4的就是 3 2 1
• 那么到达4的方法就是：到达 3 2 1 台阶的方法之和

题解核心逻辑🚶：

现在推出来了：

1. 状态表示（经验 (以某个位置结尾/以某个位置起始) + 题目要求）
   1. dp[ i ] 表示到达i个台阶一共有多少个方法
      
2. 状态转移方程：以 i 位置的状态，最近的一步，来划分问题
   1. dp[i] 分为三种情况：
   2. 从 i - 1 -> i：dp[ i - 1 ]
   3. 从 i - 2 -> i：dp[ i - 2 ]
   4. 从 i - 3 -> i：dp[ i - 3 ]
   5. 所以：dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]
      
3. 初始化：
   1. dp[0] = 1
   2. dp[1] = 1
   3. dp[2] = 2
4. 填表顺序：从左往右
5. 返回值：dp[n]

class Solution {
public:
    int waysToStep(int n) {
        //1. 状态表示：dp[n] 计算小孩上到 n 阶台阶有多少种上楼梯的方式
        //2. 状态方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3] 本质还是很上题一样
        vector<int> dp(n+3);//这里的初始化同样要注意因为可能n较小所以需要+3
        
        //3. 初始值：同样的 0 1 2，但本题的初始化就没那么简单了
        // 也希望你能很好的体会 状态表示的作用：确定每个状态点i位置的值
        dp[0] = 1;//到达0阶有几种
        dp[1] = 1;//到达1阶有几种
        dp[2] = 2;//到达2阶有几种
        if(n <= 2) return dp[n];
        //4. 方向：同样需要求 i 就得先找到 i-3... 那么就得从左往右
        for(int i = 3;i <= n;i++)
        {
            dp[i] = ((long)dp[i-1] + dp[i-2] + dp[i-3]) % 1000000007;//这里本质就是使用状态转移方程
        }
        //5. 返回dp[n]即可
        return dp[n];
    }

//写法二：
    int waysToStep(int n) {
        vector<int> dp(n + 3);

        dp[1] = 1;dp[2] = 2;dp[3] = 4; //另外一种看法忽律0台阶直接从1开始，方法类似不过多叙述

        for(int i = 4;i<=n;i++){
            dp[i] = ((long)dp[i-1] + dp[i-2] + dp[i-3]) % 1000000007;
        }
        return dp[n];
    }
//写法三：
//这里优化就不写了贴一份别人的：作者：Spectre
    int waysToStep(int n) {
        // 时间复杂度O(N)，空间复杂度O(1)
        if (n == 1 || n == 2) return n;
        if (n == 3) return 4;
        int dp1 = 1, dp2 = 2, dp3 = 4, dp4;
        for (int i = 4; i <= n; ++i) {
            dp4 = ((dp1 + dp2) % 1000000007 + dp3) % 1000000007;
            dp1 = dp2;
            dp2 = dp3;
            dp3 = dp4;
        }
        return dp4;
    }

};

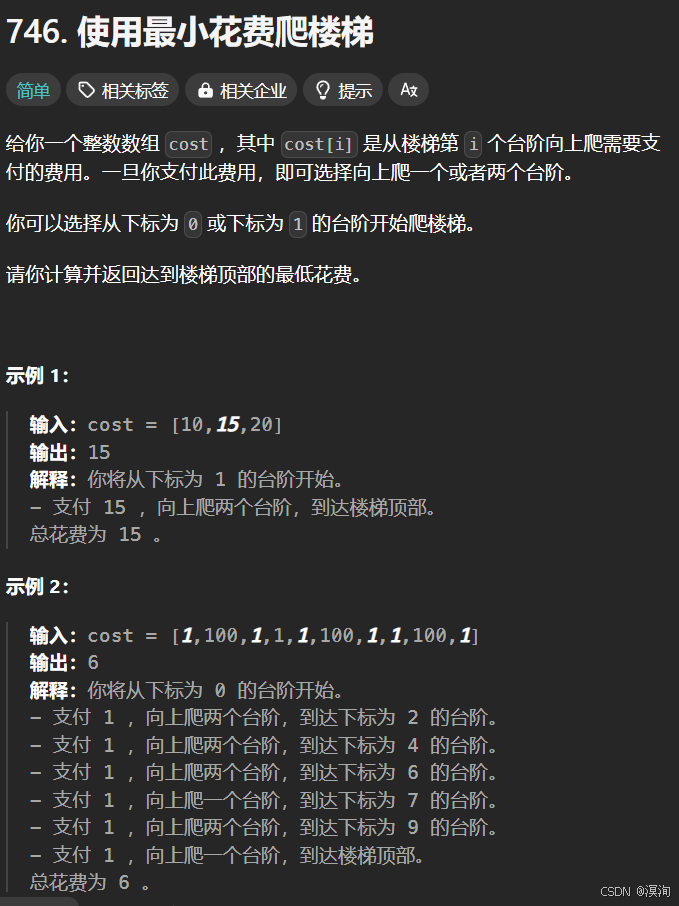
3. 使用最小花费爬楼梯🪜

题目📕：

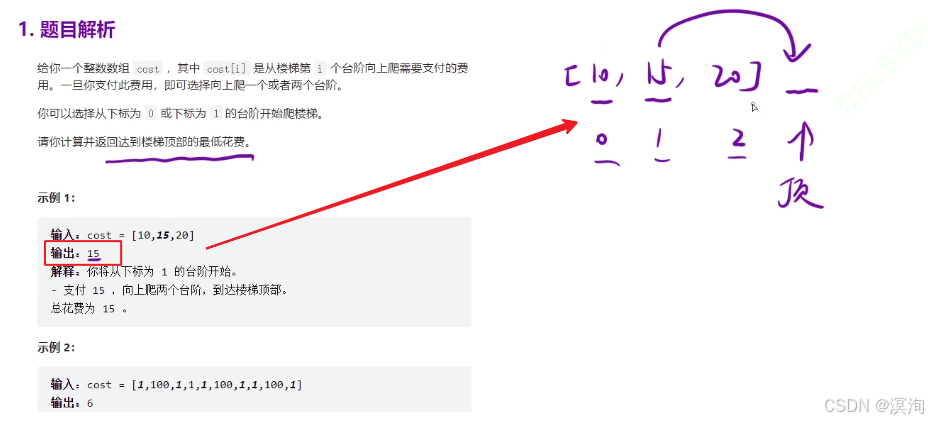
分析题目并提出，解决方法✍️：

• 楼顶在最后
  

题解核心逻辑🎈：

解法一：

1. 状态表示（经验+题目要求）：
   1. 以 i 位置为结尾，xxx：
   2. 所以：dp[ i ] 表示：到达 i 位置时，最小花费
2. 状态转移方程
   1. 用之前 或者 之后的状态，推导出dp[ i ] 的值
      
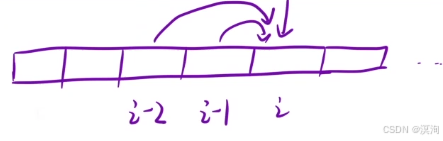
   2. 根据最近的一步，来划分问题
   3. 先到达 i - 1，然后支付 cost[ i-1 ]，走一步：dp[ i - 1] + cost[ i - 1 ]
   4. 先到达 i - 2，然后支付 cost[ i-2 ]，走两步：dp[ i - 2 ] + cost[ i - 2]
   5. 所以dp[ i ] = min( dp[ i - 1] + cost[ i - 1 ] , dp[ i - 2 ] + cost[ i - 2] )
3. 初始化（防止越界，因为会用到 i - 1 和 i - 2 两个位置的值）：
   1. 因为dp[ 0 ] = dp[ -1 ] + dp[ -2 ]这是没必要的，从题目可知
   2. 0 1 台阶是0元，所以直接从 2 开始即可
   3. 所以初始化 dp[0] = dp[1] = 0
      
4. 填表顺序：由题意从左往右
5. 返回值：dp[n]

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        // cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用
        // 爬到楼顶本质就是超过容器个数 size=3 就需要爬到4（下标3）

        // 1. dp[i]:到达第i层需要的 最小 花费
        int n = cost.size();
        vector<int> dp(n+1); 
        // 2. 状态转移方程： dp[i] = min(dp[i-1],dp[i-2]) + cost[i] 因为只能从下两层爬上来 + 当前需要的价值，注意的是cost[size]是越界的，此时+0即可
        // 3. 初始化：最小情况： dp[2] = min(dp[1],dp[0]) + cost[2] ，故初始化dp[1] dp[2] 即可
        dp[1] = cost[1];
        dp[0] = cost[0];
        for(int i = 2;i<= n;i++)
        {
            if(i == n) dp[i] = min(dp[i-1],dp[i-2]);
            else dp[i] = min(dp[i-1],dp[i-2]) +cost[i];
        }
        return dp[n];
    }
};

方法二👻：

1. 状态表示：
   1. 以 i 位置为起点，xxx
      
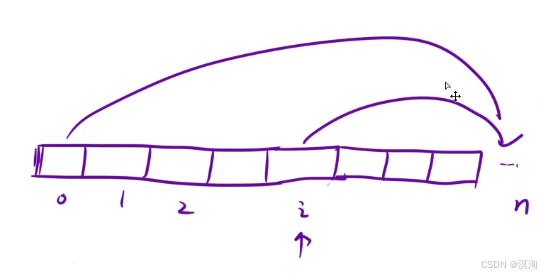
   2. dp[ i ]：从 i 位置开始，到达楼顶，此时的最小花费
2. 状态转移方程
   1. 用之前或者之后的状态推导
   2. 支付cost[i]，往后走一步，从 i + 1 位置出发到达终点 dp[ i + 1 ] + cost[ i ]
   3. 支付 cost[ i ]，往后走两步，从 i + 2 位置出发到达终点 dp[ i + 2 ] + cost[ i ]
   4. dp[ i ] = min( dp[ i + 1 ] + cost[ i ],dp[ i + 2 ] + cost[ i ])；
      
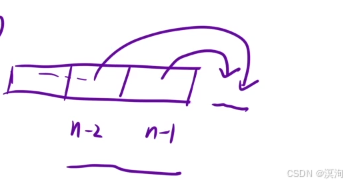
3. 初始化：
   1. dp[ n - 1 ] = cost [ n - 1 ]
   2. dp [ n - 2 ] = cost[ n - 2 ]
      
4. 填表顺序：从右往左
5. 返回值：min(dp[0]，dp[1])

这里就不扩展写了，感兴趣的可以实践下

中断总结🗒️一下：

1. 通过上述好几道题不难总结出常用的状态表示经验：
   1. 以 i 位置为结尾，xxx
   2. 以 i 位置为开始，xxx

---

🥴通过上述三道题，估计你对动态规划中的最基本的步骤和思想都有一定的认识了，下面就不将是简单的套公式了，而是结合一些内容进一步深化对动态规划的理解

也就需要你在抽象的题目中提解出动态规划~~🤔

🤓本质也就是：状态表示不简单了、状态方程也没那么好推导了

---

4. 解码方法

题目🪜：

分析题目并提出，解决方法✍️：

本题如何想到的呢：从最后一个节点来看，不难发现规律：

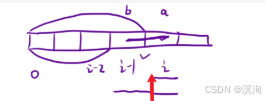
1. 要求第i位置的能否解码，就只用考略
   1. 当前位置i是否符合（0 <= i <= 9）
   2. i位置与i-1位置结合时是否符合(10 <= i-1 + i <= 26)
2. 要求总共的解码个数，则是通过dp表存储每个节点的解码个数，最小的情况是很容易推算的，所以使用动规中的dp表是能进行存储的
3. 通过上面两个想法也就不难得出状态转移方程如何计算
   1. 判断能否解码的两种方法，看这两种方法那个符合条件，若符合条件就记录上存储进dp表中
   2. 若不能解码的当然就不计算
   3. 具体见下面详细五步

题解核心逻辑🎈：

1. 状态表示：
   1. 以 i 结尾时，解法方法的总数
2. 状态转移方程
   1. 根据最近的一步划分问题：
   2. 分为两种情况：
      1. dp[ i ]单独解码（ 1 ~ 9 ）：解码成功（个数为 dp[ i -1 ]：因为本质就是拼接了一个新字母🤔这里好好理解下，并不用+1哦），失败则为0
      2. dp[ i ] 与 dp[ i - 1 ] 结合解码（ 10 ~ 26 ） ：解码成功（dp[ i - 2 ] 本质就是拼接两个新字母），失败则为0
         
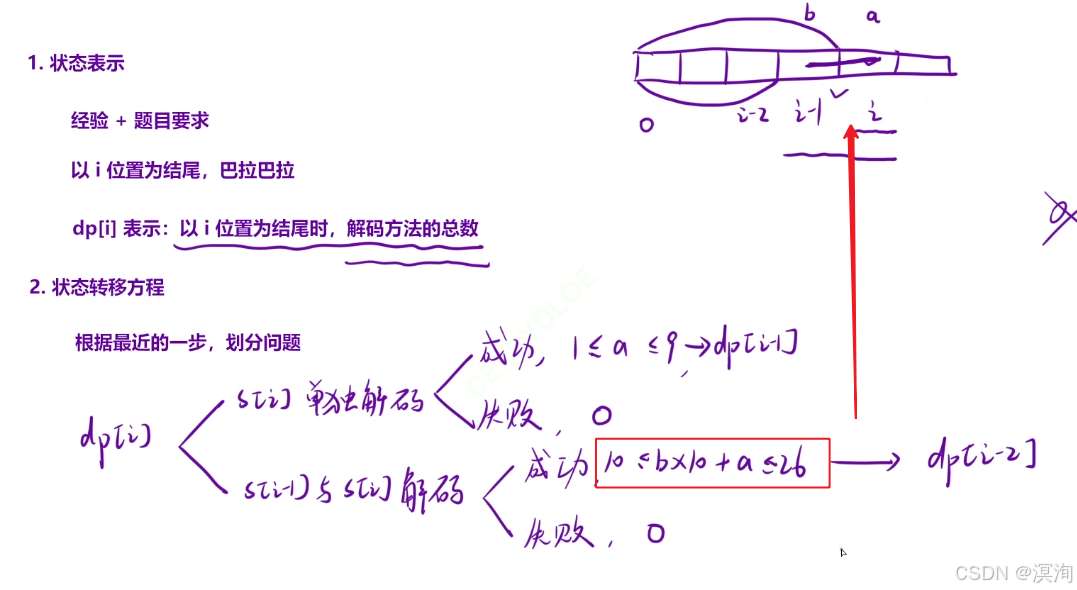
3. 初始化：dp[ 0 ] 、dp[ 1 ]
4. 填表顺序：根据状态转移方程得知从左往右
5. 返回值：dp[ n - 1 ]，n - 1最后一个位置

优化：处理边界问题以及初始化问题的技巧🤓

整个数组多开一位，然后通过使用这个多开的一位虚拟节点的初始化来帮助运算

注意的事项：

1. 虚拟节点的初始化是根据题目意思来的，保证后面填表的正确
   1. 一般来说填写0
   2. 但本题对于该虚拟节点的使用，为了求原dp表中的dp[ 1 ] 时使用的 dp[ i - 2 ]
   3. 因为假设 dp[ 1 ] 和 移动后就变成了 dp[ 2 ]，此时要求dp[ 2 ] 需要dp[ 1 ] 和 dp [ 0 ]
   4. dp [ 1 ] 本质就是原dp数组中的dp[ 0 ] 所以不会有问题
   5. 但dp[ 0 ] 就需要我们自己控制，回顾状态转移方程，这里dp[ i - 2 ]的作用是当 i 和 i - 1结合成功时取的值，所以填1（因为前面也没字符判断了，所以填1给到dp[2]，代表正确）
      
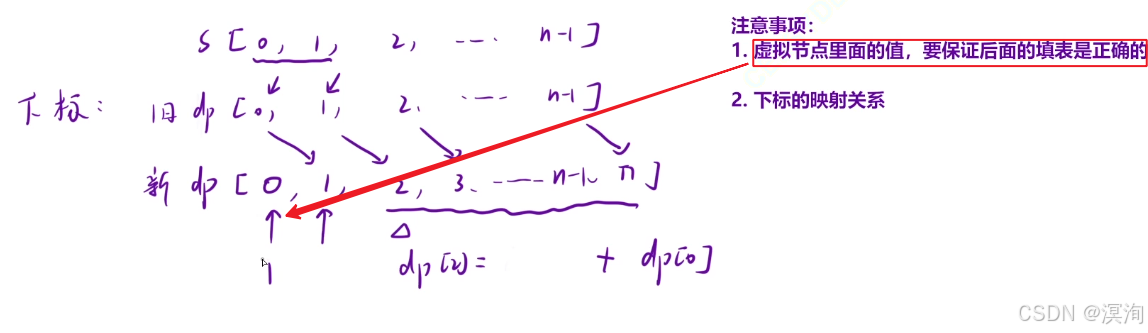
2. 注意下标的映射关系，在真正使用dp时，因为dp表是多一格，对于s字符串中的下标要 - 1：s[i-1]

class Solution {
public:
    int dp[101] = {};
    int numDecodings(string s) {
        //初始化 0 和 1
        dp[0] = 1;//虚拟节点
        if( 1 <=  s[0] - '0' &&  s[0] - '0' <= 9) dp[1] = 1 ;//原dp[0]

//移动s字符下标完成：
        for(int i = 2; i <= s.size();i++)
        {
            //单个字符
            int onechar = s[i - 1] - '0'; 
            if( 1 <= onechar && onechar <= 9) dp[i] += dp[i-1];
            
            //两个字符
            int combine = (s[i - 2] - '0') * 10 + onechar;
            if(10 <= combine && combine <= 26) dp[i] += dp[i-2];
            
            if(dp[i] == 0) return 0;
        }
        return dp[s.size()];
    }
};

解法二：
class Solution {
public:
    int numDecodings(string s) {
        //dp[i]：以i位置结尾的解码个数：
        //dp[i] = dp[i-1] + dp[i-2]，其中若若不能解码则不进行相加，或者加0
        //初始化：因为s.length >= 1，所以需要一个多的空位，来特殊处理等于1的情况
        int n = s.size();
        vector<int> dp(n+2);//结果存在n下标
        dp[0] = 1; //默认解码个数为1次
        dp[1] = 1; //默认解码个数为1次
        if(s[0] == '0') return 0;

//处理dp下标完成存储效果
        for(int i = 0; i < n;i++)
        {
            //不要简单的字符判断！！！！！！！！！！！
            // if(i-1 >= 0 && s[i-1] - '0' >= 1 && s[i-1] - '0' <= 2 && 
            //    s[i] - '0' >= 0 && s[i] - '0' <= 6) dp[i+2] += dp[i];
            int val = s[i] - '0';
            if(val >= 1 && val <= 9) dp[i+2] += dp[i+1];
           
            
            int combine = i-1 >= 0 ? ( s[i-1] - '0') * 10 + val : -1;
            if(combine >= 10 && combine <= 26)  dp[i+2] += dp[i];
        }

        return dp[n+1];
    }
};

对于需要判断两位或者多位数字时，不要图方便使用字符判断，而是将他转换为数字😭