AVL树知识总结

AVL树

概念性质

一颗AVL树或是空树，或者具有一下性质的二叉搜索树：左右都是AVL树，左右子树高度差的绝对值不超过1

AVL树有n个结果，高度保持在O（logN）搜索时间复杂度O(logN）

模拟实现插入

定义：左子树，右子树，父亲节点，自身值，平衡因子

复制代码

static class TreeNode{
        public TreeNode left;
        public TreeNode right;
        public TreeNode parent;
        public int val;
        public int bf;//平衡因子

        public TreeNode(int val) {
            this.val = val;
        }
    }

插入

1.先将数据插入AVL树中（和二叉搜索树一样）

复制代码

  public static boolean insert(int val){
        TreeNode node=new TreeNode(val);
        if(root==null){
            root=node;
            return true;
        }
        TreeNode cur=root;
        TreeNode parent=null;
        while(cur!=null){
            if(cur.val==val){
                return false;
            }else if(cur.val>val){
                parent=cur;
                cur=cur.left;
            }else{
                parent=cur;
                cur=cur.right;
            }
        }
        //cur=null
        if(parent.val>val){
            parent.left=node;
        }else{
            parent.right=node;
        }
        node.parent=parent;
        cur=node;
        //调整平衡因子
        while(parent!=null){
            if(cur==parent.left){
                parent.bf--;
            }else{
                parent.bf++;
            }
            if(parent.bf==0){
                break;
            }else if(parent.bf==1||parent.bf==-1){
                //继续向上调整
                cur=parent;
                parent=cur.parent;
            }else{
                if(parent.bf==2){//右树高度高
                    if(cur.bf==1){
                        rotateLeft(parent);
                    }else{
                        rotateRL(parent);
                    }
                }else{
                    if(cur.bf==-1){
                        rotateRight(parent);
                    }else{
                        rotateLR(parent);
                    }
                }
            }
        }
        return  true;
    }

2.插入后，根据平衡因子进行调整

当parent.bf==0时就平衡了，不需要再向上调整了

旋转

复制代码

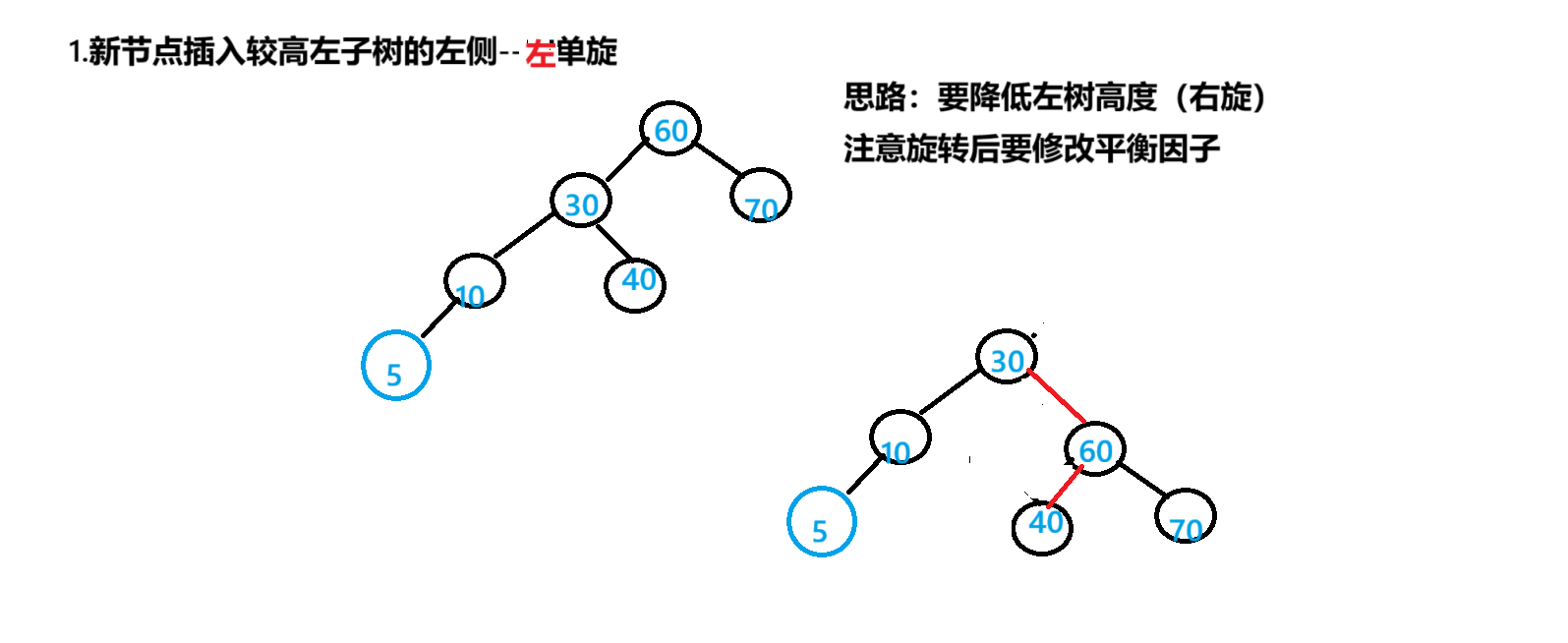
private static void rotateLeft(TreeNode parent) {
        TreeNode subR=parent.right;
        TreeNode subRL=subR.left;
        parent.right=subRL;
        if(subRL!=null){
            subRL.parent=parent;
        }
        TreeNode pParent=parent.parent;
        parent.parent=subR;
        if(parent==root){
            root=subR;
            subR.parent=null;
        }else{
            if(pParent.left==parent){
                pParent.left=subR;
            }else{
                pParent.right=subR;
            }
            subR.parent=pParent;
        }
        subR.bf=parent.bf=0;
    }

复制代码

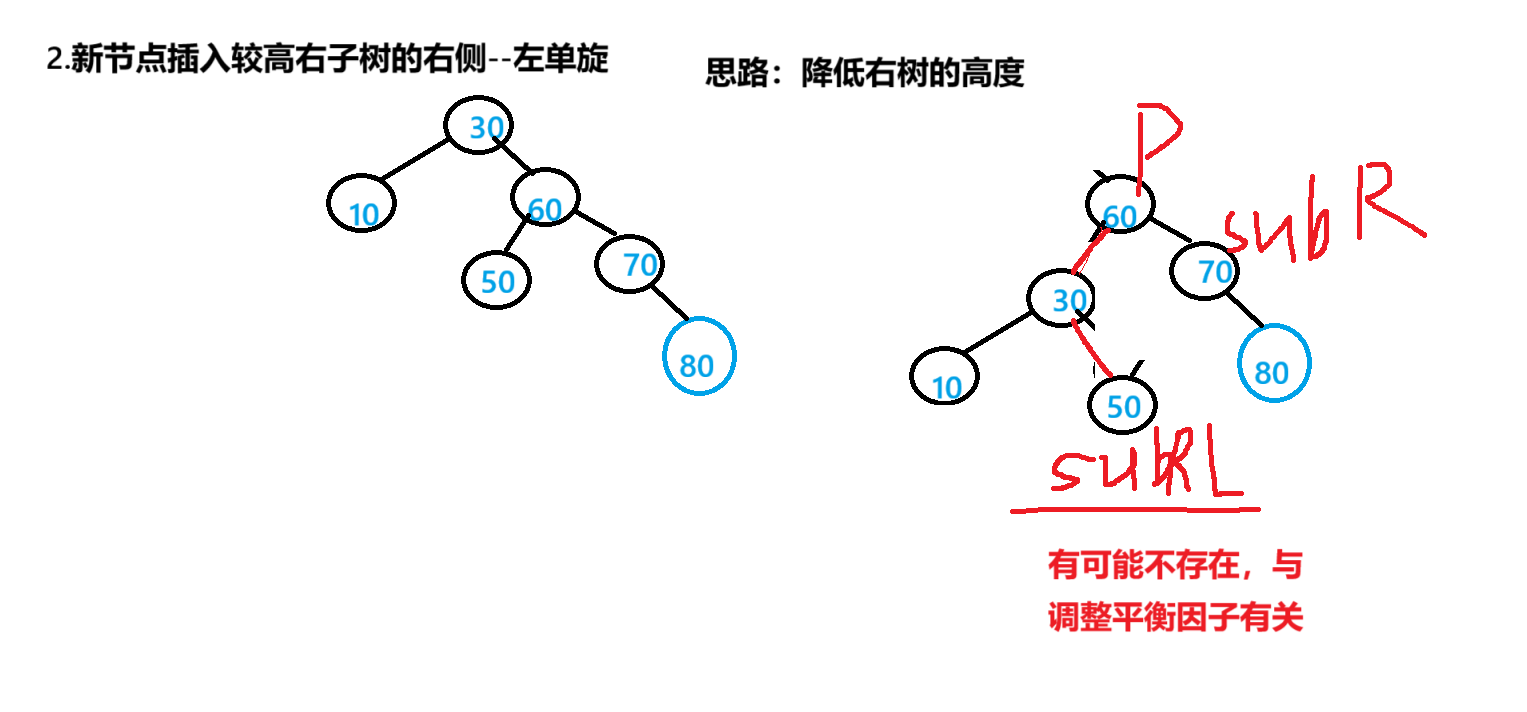
 private static void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;

        parent.left = subLR;
        subL.right = parent;
        //没有subLR
        if(subLR != null) {
            subLR.parent = parent;
        }
        //必须先记录
        TreeNode pParent = parent.parent;
        parent.parent = subL;
        //检查 当前是不是就是根节点
        if(parent == root) {
            root = subL;
            root.parent = null;
        }else {
            //不是根节点，判断这棵子树是左子树还是右子树
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
        subL.bf = 0;
        parent.bf = 0;
    }

复制代码

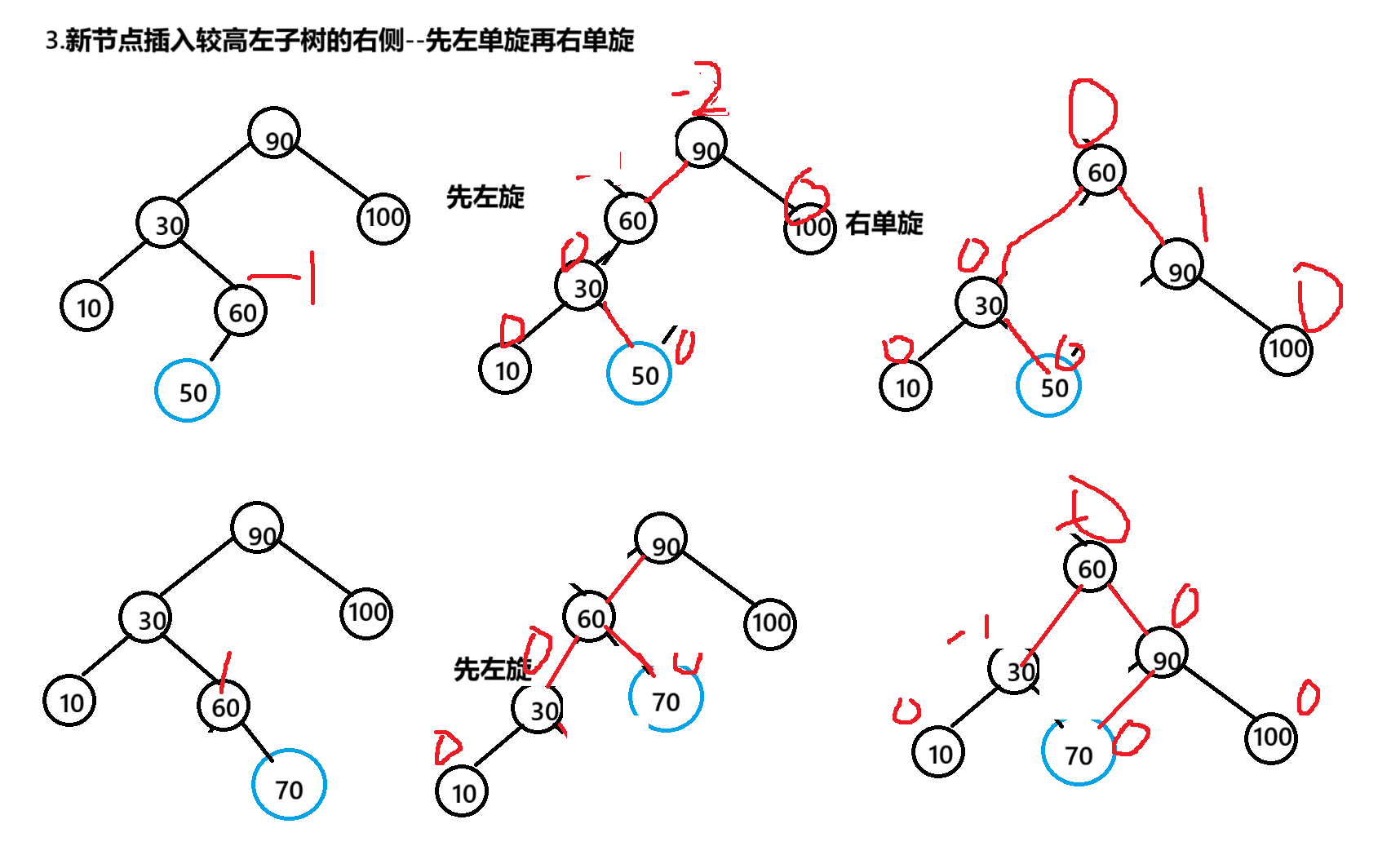
 private static void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;

        rotateLeft(parent.left);
        rotateRight(parent);
        if(bf == -1) {
            subL.bf = 0;
            subLR.bf = 0;
            parent.bf = 1;
        }else if(bf == 1){
            subL.bf = -1;
            subLR.bf = 0;
            parent.bf = 0;
        }
    }

复制代码

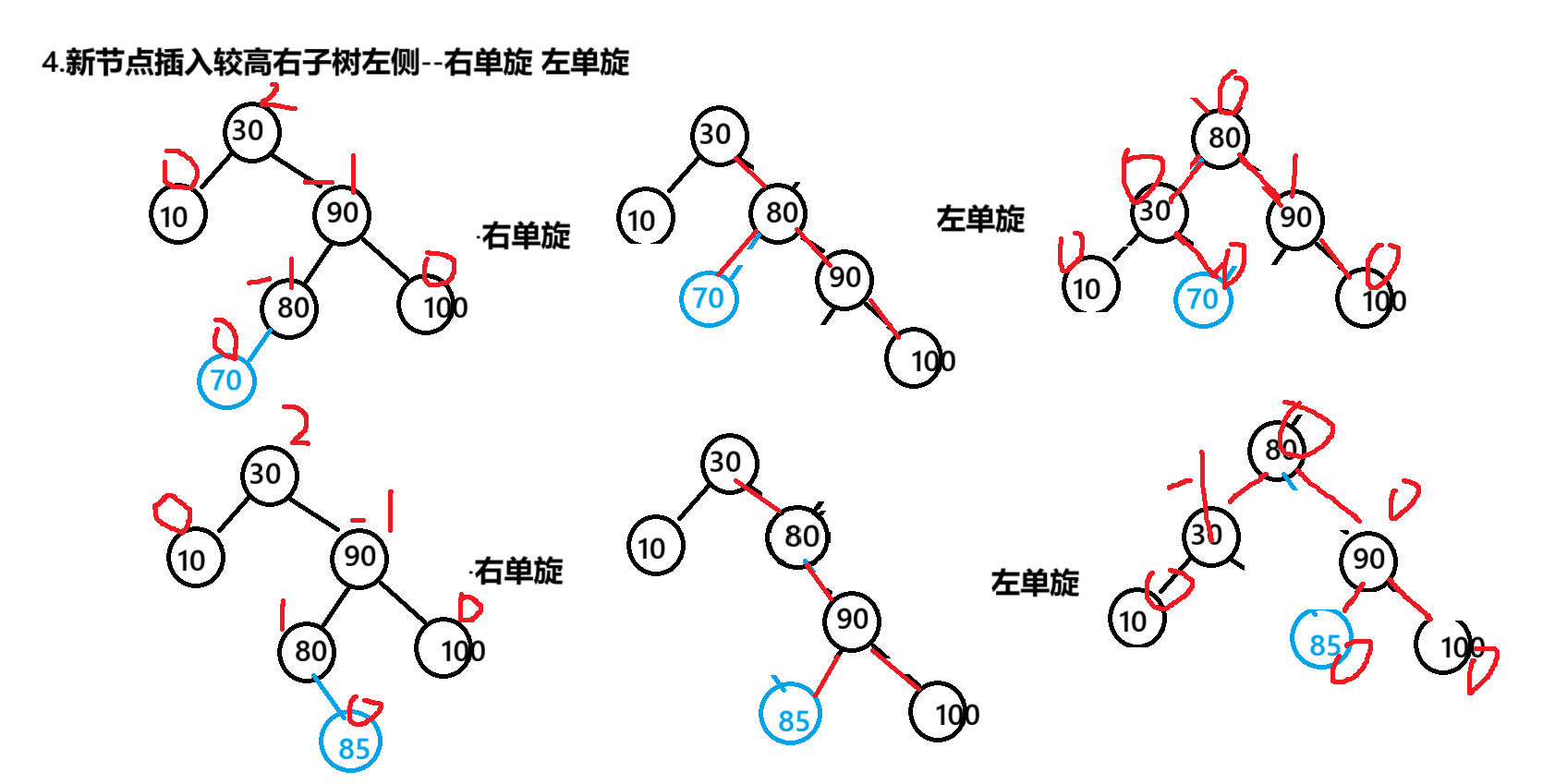
 private static void rotateRL(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;

        rotateRight(parent.right);
        rotateLeft(parent);

        if(bf == 1) {
            parent.bf = -1;
            subR.bf = 0;
            subRL.bf = 0;
        }else if(bf == -1){
            parent.bf = 0;
            subR.bf = 1;
            subRL.bf = 0;
        }
    }

验证当前树是否为AVL树

高度平衡的二叉搜索树（不能遍历AVL树，因为bf是我们手动设置的，可能会出错）

复制代码

  private int height(TreeNode root) {
        if(root == null) return 0;
        int leftH = height(root.left);
        int rightH = height(root.right);

        return leftH > rightH ? leftH+1 : rightH+1;
    }

    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        int leftH = height(root.left);
        int rightH = height(root.right);

        if(rightH-leftH != root.bf) {
            System.out.println("这个节点："+root.val+" 平衡因子异常");
            return false;
        }

        return Math.abs(leftH-rightH) <= 1
                && isBalanced(root.left)
                && isBalanced(root.right);
    }

AVL树的删除思路

1.找到要删除节点

2.按二叉搜索树删除规则删除节点

3.更新平衡因子

性能分析

AVL树的平衡是通过大量旋转换来的，适合查找高效且有序的数据结构，而且数据个数为静态的