摘要
本文系统地概述了量子计算,从其利用量子叠加与纠缠的核心原理、多样的物理实现方案、复杂的软硬件架构,到实现可逆计算的逻辑门与数学基础,为初学者提供了一个全面而深刻的认识框架。
Abstract
This article provides a systematic overview of quantum computing, covering its core principles of leveraging quantum superposition and entanglement, diverse physical implementation schemes, complex software and hardware architecture, as well as the logic gates and mathematical foundations that enable reversible computation. It offers a comprehensive and profound framework for beginners to understand the field.
1 什么是量子计算
量子计算是一种利用量子力学特性( 叠加和纠缠)来进行计算的新型计算模式。

经典计算的基本单位是比特,其状态只能是确定的0或1;而量子计算的基本单位是量子比特,其状态可以用一个向量表示,即 a|0⟩ + b|1⟩,其中 a 和 b 是复数,且必须满足 |a|² + |b|² = 1 这个条件。这个公式意味着一个量子比特可以同时处于0和1的叠加状态,其概率幅分别由 a 和 b 决定。
量子计算不是一个抽象的理论,它的实现依赖于具体的物理系统。下面这张图片对比了五种制造量子比特的主流实验方案。(超导环中电阻为零的振荡电流、被电磁场和激光禁锢的离子、硅片中人造的"量子点"原子、基于马约拉纳费米子等)
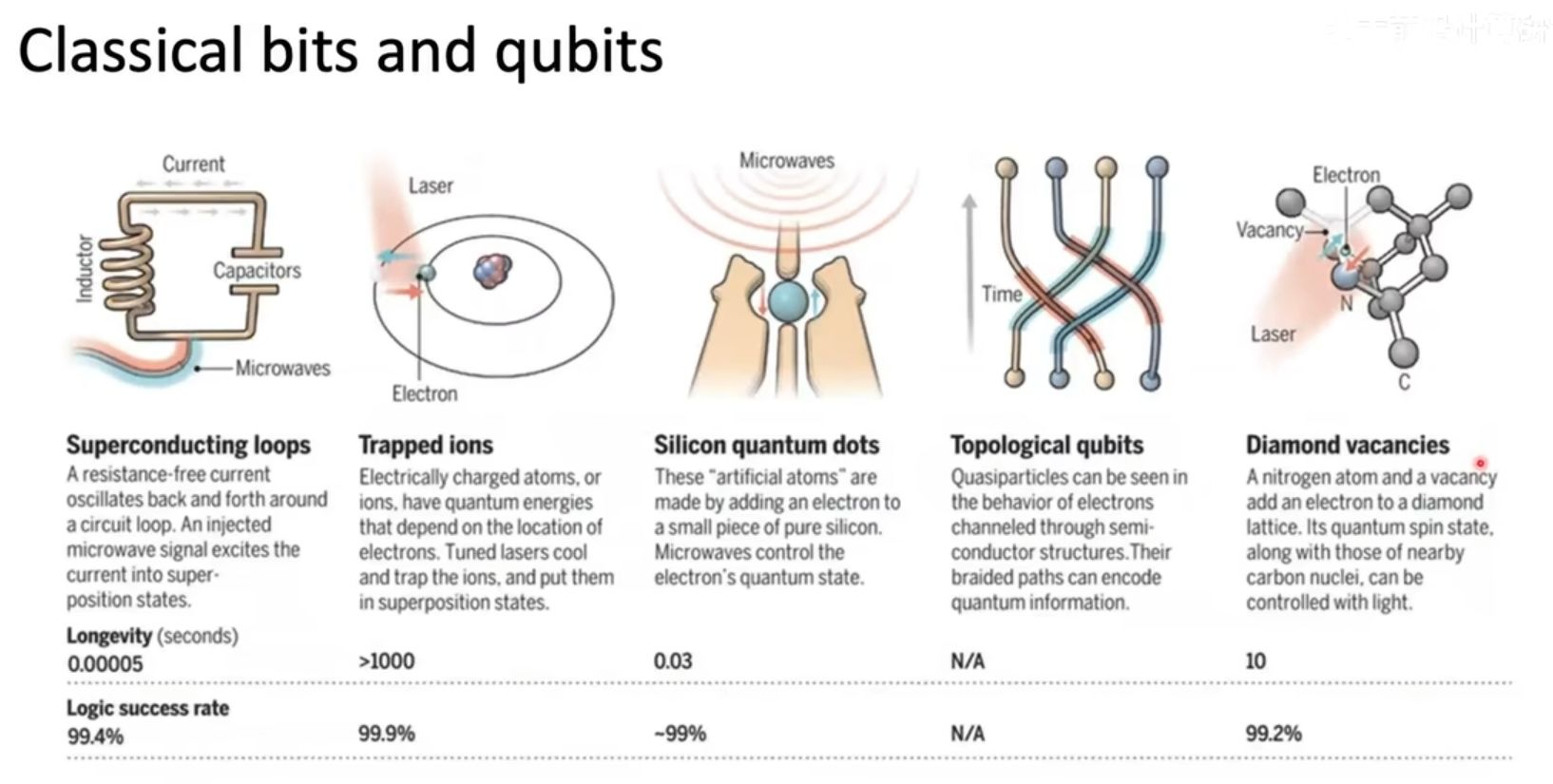
上述这些方案的最终目标都是为了创造出能够保持量子态(叠加和纠缠)足够长时间(寿命),并能以极高准确度执行操作(逻辑成功率)的物理平台。
老师特别推荐学习平台:

下图使用了Google开发的Cirq量子计算框架,这段代码完整演示了一个核心量子操作的实现。

它创建了两个量子比特,对其施加哈达玛门(H)产生叠加态,再通过受控非门(CNOT)建立量子纠缠,最后进行测量并重复模拟10次。代码下方的终端输出结果(两行完全相同的测量序列"1100010001")直观验证了量子纠缠的特性------当两个比特纠缠时,对其中一个的测量结果会瞬间决定另一个的状态。
从宏观架构和物理实现两个角度,系统地描绘了构建一台实用量子计算机所涉及的多层次技术栈。
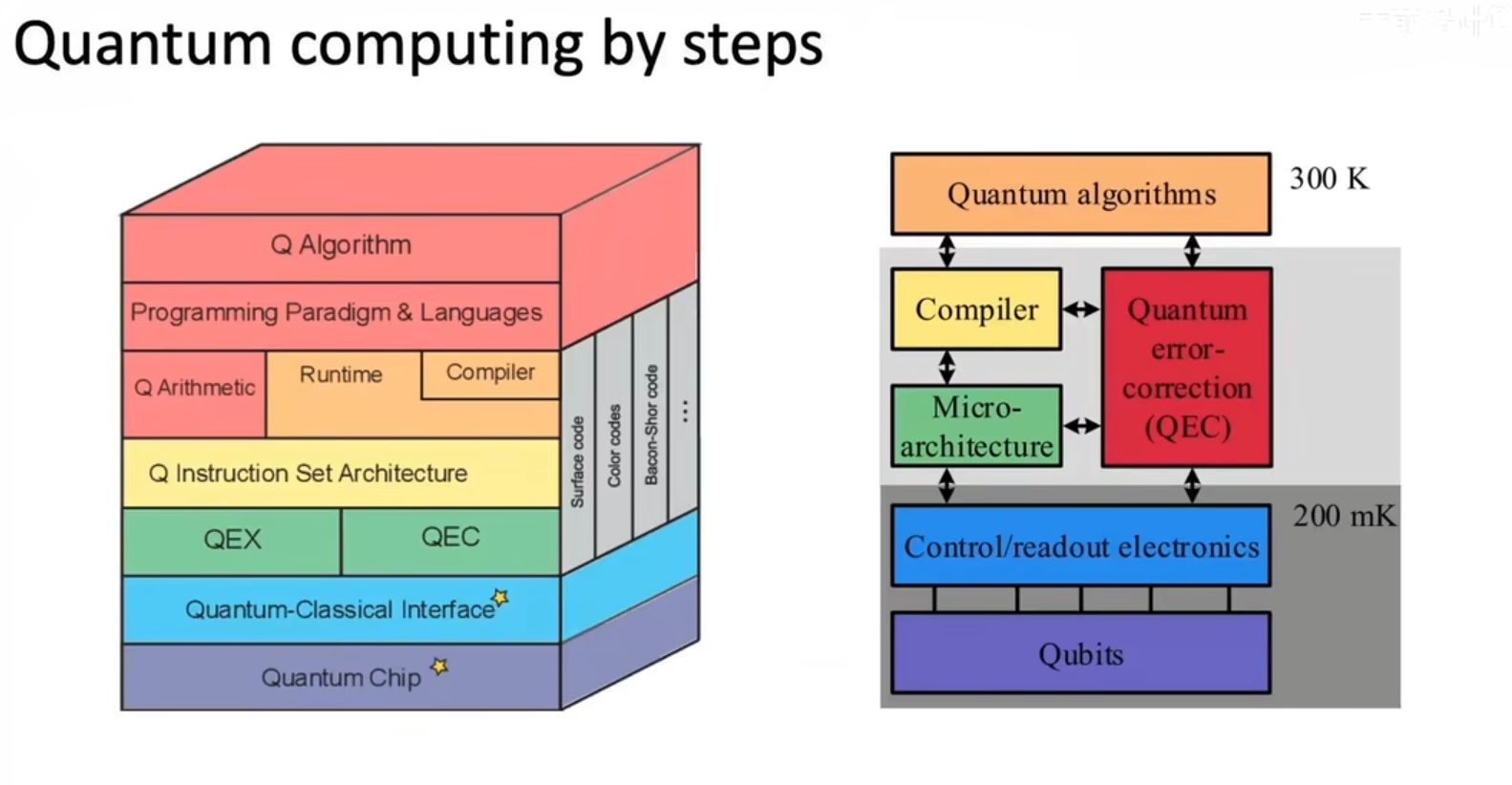
图中左侧的立方体结构代表了一个从底层硬件到顶层应用的自上而下的抽象层次模型。它从最底层的物理硬件开始,向上依次是量子算术与逻辑、指令集架构、编程范式与语言,最终到达顶层的量子算法。这个模型展示了我们如何将复杂的量子算法一步步"翻译"和"分解"为硬件可以执行的基本操作。旁边列出的Surface code、Color codes等,则指明了在各个层级实现量子纠错的不同方案,这是确保计算可靠性的核心。
右侧的流程示意图则补充了一个自下而上的物理实现视角,并特别强调了工作温度这一关键物理约束。它从需要深度制冷至极低温的量子比特本身开始,向上经过控制和读取电子设备、微架构,最终到达在室温下运行的编译器和量子算法。这个温度梯度清晰地表明,一台量子计算机是同时运行在极低温和室温的混合系统。图中特别标注的量子纠错与编译器和微架构相连,说明纠错不是一个独立的步骤,而是需要软硬件协同设计的核心任务。
2 门的逻辑运算
下图是经典基础的门的逻辑图。
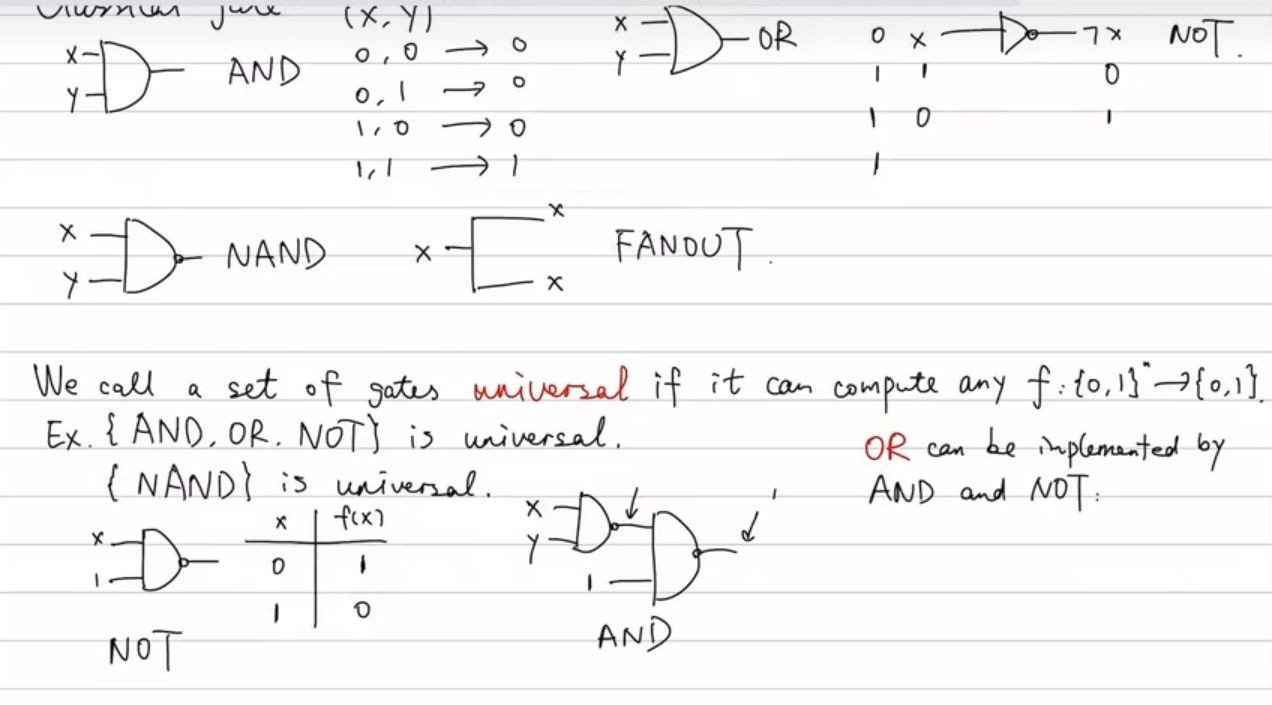
托佛利门作为通用逻辑门的重要特性。它通过两个简洁的电路示意图,证明了仅使用托佛利门这一种三量子比特门,就能构建出所有经典计算中所需的基本逻辑操作,从而实现任何经典计算功能。(由于任何复杂的经典计算电路最终都可以由与门和非门组合而成,而托佛利门又能独立实现这两种基本功能,所以它本身就是一个 通用门。)
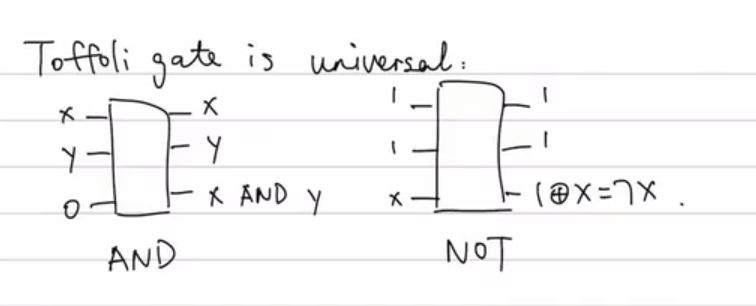
通过引入辅助比特(Ancilla bits) 和可逆逻辑门来实现任何传统计算的可逆版本。

通过辅助比特的引入和可逆门的操作,所有输入信息均被保留,使得计算过程在物理上可逆(如量子计算中所有操作必须满足可逆性)。垃圾比特的存在表明,为实现可逆性需要付出额外的资源代价。该原理是连接经典计算与量子计算的桥梁,为量子计算机执行经典算法提供了理论基础。
从量子比特的基本定义出发,说明其状态是一个二维复向量,形式为 (a0a1),其中 a0和 a1是复数,且其模长的平方和必须为 1,这个条件保证了测量概率的总和为 1。图中引入了 "计算基" 的概念,即 ∣0⟩和 ∣1⟩这两个标准正交基向量,并开始使用 Dirac 的 "bra-ket"符号 来表示它们。

ket" (如 ∣ψ⟩)代表列向量,而 "bra" (如 ⟨ψ∣)代表其共轭转置(即行向量)。两者的结合 ⟨ϕ∣ψ⟩构成"bracket",表示内积。图片通过具体的矩阵运算示例,展示了如何计算两个量子态之间的内积,并再次强调了态向量的归一化条件 ⟨ψ∣ψ⟩=1。

推导出任意单量子态都可以用两个角度参数 (θ,ϕ)和一个全局相位因子 γ来表示:∣ψ⟩=eiγ(cos2θ∣0⟩+eiϕsin2θ∣1⟩)。由于全局相位 γ在物理上不可观测,通常可以忽略(令 γ=0),从而得到最常用的表达式:∣ψ⟩=cos2θ∣0⟩+eiϕsin2θ∣1⟩。这个公式揭示了量子态可以在一个被称为布洛赫球的单位球面上进行表达。

3 学习总结
学习了量子计算的核心脉络:从利用叠加与纠缠原理的量子比特,到超导、离子阱等多样化的物理实现方案;从需要极低温与环境控制的硬件架构,到依赖可逆计算与通用逻辑门的运算基础;最终深入至用狄拉克符号和布洛赫球描述量子态的数学本质,为理解这一前沿领域构建了从理论到实践的完整认知框架。
注意:本次周报是用b站北大前沿计算中心的视频进行学习的