【1】引言
前序学习进程中,已经了解到可以将满足正态分布变量的损失函数求解转化为线性回归损失函数求解。
这里先回忆一下正态分布函数式:
p ( x ) = 1 2 π σ 2 e x p ( − 1 2 σ 2 ( x − μ ) 2 ) p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2) p(x)=2πσ2 1exp(−2σ21(x−μ)2)
要想在PyTorch里面用好这个方程,掌握如何控制输入输出获得图像是一个直接、高效的方法。
【2】Numpy和PyTorch模块绘图
【2.1】Numpy绘制正态分布函数图
先练习比较熟悉的Numpy绘图,这里直接给出完整代码:
python
# 引入模块
import matplotlib.pyplot as plt
import numpy as np
import math
# 自定义函数
# 传入参数后,函数输出正态分布函数的计算结果
def normal(x, mu, sigma):
p = 1 / math.sqrt(2 * math.pi * sigma**2)
return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
x = np.arange(-7, 7, 0.01)
params = [(0, 1), (0, 2), (3, 1)]
# 分别绘制每条曲线,而不是一次性传递所有曲线
# 每次输入的均值mu和标准差均不同
for mu, sigma in params:
plt.plot(x, normal(x, mu, sigma), label=f'mean {mu}, std {sigma}')
plt.legend()
plt.show()由于自变量x的范围已经确定,所以改变代表均值和标准差的params矩阵中的每一组值都可以移动函数图像。
例如这里的(0,1)代表均值为0,标准差为1。对应的图像就是以x=0轴为对称轴,以1为标准差的正态分布图像。
代码运行后获得的图像为:
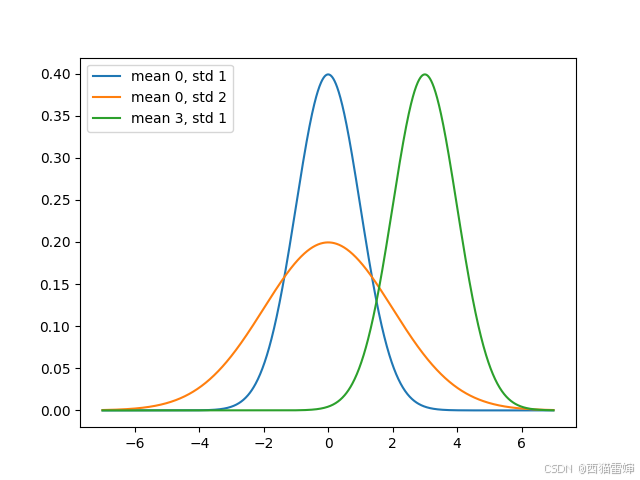
有图像可以看出,均值所在的位置就是对称轴的位置;标准差越大,图像越低矮。
【2.2】PyTorch绘制正态分布函数图
使用PyTorch绘图的代码可以参考Numpy的代码,这里直接给出完整代码:
python
# 引入模块
import torch
import math
import matplotlib.pyplot as plt
# 生成x轴数据(使用PyTorch而非NumPy)
x = torch.arange(-7.0, 7.0, 0.01) # 从-7到7,步长0.01
# 定义要绘制的正态分布参数 (均值, 标准差)
params = [(0, 1), (0, 2), (3, 1)]
# 绘制每条正态分布曲线
for mu, sigma in params:
# 使用PyTorch计算正态分布的概率密度函数
# 计算系数部分
coefficient = 1 / torch.sqrt(2 * torch.tensor(math.pi) * sigma ** 2)
# 计算指数部分
exponent = -0.5 / (sigma ** 2) * (x - mu) ** 2
# 概率密度值
y = coefficient * torch.exp(exponent)
# 绘制曲线
plt.plot(x.numpy(), y.numpy(), label=f'mean {mu}, std {sigma}')
plt.legend()
# 设置图表属性
plt.grid(True, alpha=0.3)
plt.show()代码运行后输出的图像与2.1节一致。
需要注意的细节是,torch.sqrt()函数是对张量取平方根,所以其内部的变量必须定义为张量,这就是torch.tensor(math.pi)定义的必要性。
实际上torch模块也具有自动转化功能,即使不使用torch.tensor(math.pi),直接写作 coefficient = 1 / torch.sqrt(2 * math.pi * sigma ** 2),代码也可以运行。
【3】总结
学习了使用Numpy和PyTorch模块绘制正态分布函数图的基本技巧。