「日拱一码」098 机器学习可解释——PDP分析

[PDP 分析介绍](#PDP 分析介绍)

什么是PDP？

为什么需要PDP？

PDP是如何工作的？

PDP的优缺点

代码示例

如何解读PDP图

PDP 分析介绍

什么是PDP？

部分依赖图（PDP） 是一种用于解释机器学习模型预测结果的工具。它显示了一个或两个特征对机器学习模型的预测结果的边际效应。简单来说，PDP可以回答这样一个问题："当某个特征发生变化时，模型的预测平均会如何变化？"

为什么需要PDP？

模型透明化：复杂的模型（如随机森林、梯度提升树、神经网络）通常是"黑盒"，难以理解。PDP帮助我们理解模型是如何使用特征进行预测的。
验证直觉：检查特征与目标之间的关系是否符合领域知识或直觉。
检测异常关系：发现反直觉或非线性的关系。

PDP是如何工作的？

**1. 选择目标特征：**首先选择一个或两个你感兴趣的特征。

**2. 生成网格值：**在目标特征的取值范围内生成一系列的值。

3. 干预与预测：

对于网格中的每一个值，将数据集中所有样本的该特征值都替换为这个值。
用训练好的模型对这些"干预后"的数据集进行预测，并计算预测的平均值。

**4. 绘制图表：**在x轴上绘制网格值，在y轴上绘制对应的平均预测值。

PDP的优缺点

优点：

原理简单，易于理解和实现。
解释直观：曲线的高度表示预测值的大小。

缺点：

由于使用特征取值的边际平均值，可能会掩盖异质性效应（即假设特征间没有交互作用，但实际上可能存在）。
对于高基数或分类特征，计算可能较慢。
如果特征间存在强相关性，PDP可能会给出不现实的数据点（例如，在"年龄"很高的情况下强行设置"教育年限"很低，这可能在实际中不会同时出现）。

改进：为了克服PDP的缺点，可以考虑使用个体条件期望图（ICE），它显示的是每个样本的预测变化，而不仅仅是平均值，从而能揭示异质性。

代码示例

python 复制代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_friedman1
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import PartialDependenceDisplay
from sklearn.model_selection import train_test_split

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成模拟数据
print("生成模拟数据...")
X, y = make_friedman1(n_samples=1000, n_features=5, noise=0.1, random_state=42)
feature_names = [f'特征_{i}' for i in range(X.shape[1])]

# 2. 创建数据框
df = pd.DataFrame(X, columns=feature_names)
df['目标值'] = y

print("数据前5行:")
print(df.head())
#        特征_0      特征_1      特征_2      特征_3      特征_4        目标值
# 0  0.374540  0.950714  0.731994  0.598658  0.156019  16.778564
# 1  0.155995  0.058084  0.866176  0.601115  0.708073  12.278795
# 2  0.020584  0.969910  0.832443  0.212339  0.181825   5.828467
# 3  0.183405  0.304242  0.524756  0.431945  0.291229   7.623226
# 4  0.611853  0.139494  0.292145  0.366362  0.456070   9.511135
print(f"\n数据形状: {df.shape}")  # (1000, 6)

# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 4. 训练随机森林模型
print("\n训练随机森林模型...")
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)

# 评估模型
train_score = model.score(X_train, y_train)
test_score = model.score(X_test, y_test)
print(f"训练集R²分数: {train_score:.4f}")
print(f"测试集R²分数: {test_score:.4f}")
# 训练集R²分数: 0.9848
# 测试集R²分数: 0.9125

# 5. 创建单个特征的PDP图
print("\n生成部分依赖图...")
fig, ax = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('部分依赖图(PDP)分析', fontsize=16, fontweight='bold')

# 分析前4个特征
for i, feature_idx in enumerate([0, 1, 2, 3]):
    row, col = i // 2, i % 2

    PartialDependenceDisplay.from_estimator(
        estimator=model,
        X=X_test,
        features=[feature_idx],
        grid_resolution=20,
        ax=ax[row, col],
        line_kw={'color': 'blue', 'linewidth': 3}
    )

    ax[row, col].set_title(f'特征 {feature_idx} ({feature_names[feature_idx]}) 的PDP')
    ax[row, col].set_ylabel('预测目标值')
    ax[row, col].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 6. 创建两个特征的交互PDP图
print("生成特征交互图...")
fig, ax = plt.subplots(1, 2, figsize=(15, 6))

# 特征0和1的交互
PartialDependenceDisplay.from_estimator(
    estimator=model,
    X=X_test,
    features=[(0, 1)],
    grid_resolution=15,
    ax=ax[0]
)
ax[0].set_title('特征0和特征1的交互PDP')

# 特征2和3的交互
PartialDependenceDisplay.from_estimator(
    estimator=model,
    X=X_test,
    features=[(2, 3)],
    grid_resolution=15,
    ax=ax[1]
)
ax[1].set_title('特征2和特征3的交互PDP')

plt.tight_layout()
plt.show()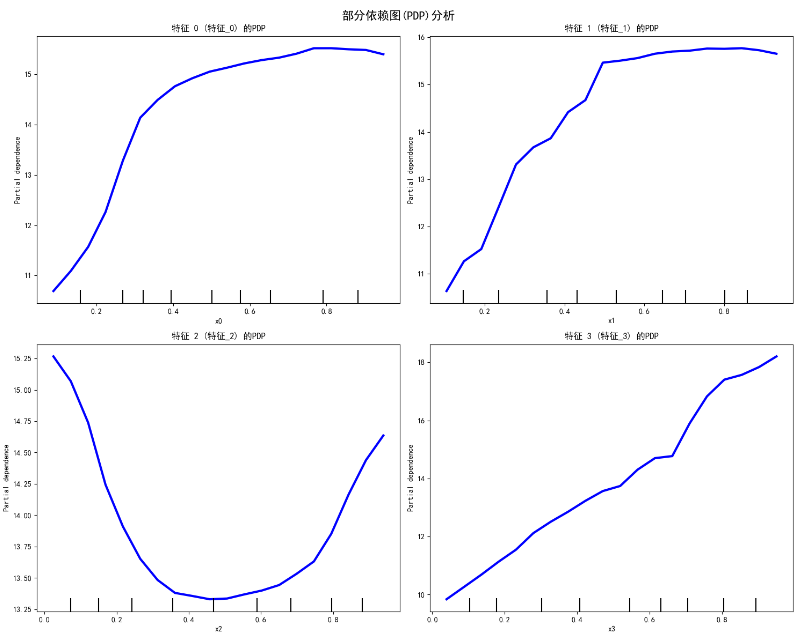

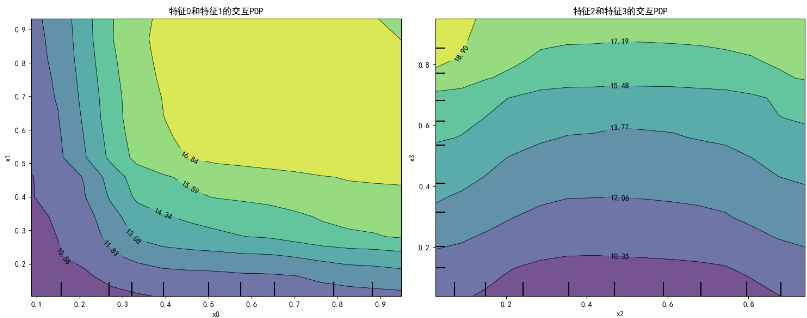
如何解读PDP图

线性关系：如果PDP曲线呈直线，说明特征与目标呈线性关系
非线性关系：曲线形状揭示复杂的非线性关系
特征重要性：曲线波动越大，特征对预测的影响越大
交互效应：交互PDP图显示两个特征如何共同影响预测