一. 参考文献
1. 随机共振（Stochastic Resonance，SR）及其在生物、工业中的应用：
**[1]**Gammaitoni L .Stochastic resonance and the dithering effect in threshold physical systems[J].Physical review. E, Statistical physics, plasmas, fluids, and related interdisciplinary topics, 1995, 52(5):4691-4698.DOI:10.1103/PhysRevE.52.4691.
**[2]**Fauve S, Heslot F. Stochastic resonance in a bistable system[J]. Physics Letters A, 1983, 97(1-2): 5-7
[3] 胡茑庆 -.随机共振微弱特征信号检测理论与方法[M].国防工业出版社,2012.
[4] Z. Shi, Z. Liao and H. Tabata, "Enhancing Performance of Convolutional Neural Network-Based Epileptic Electroencephalogram Diagnosis by Asymmetric Stochastic Resonance," in IEEE Journal of Biomedical and Health Informatics, vol. 27, no. 9, pp. 4228-4239, Sept. 2023, doi: 10.1109/JBHI.2023.3282251.
2. 广义随机共振（Generalized SR，GSR）及其在工业中的应用： Kehan Chen, Yuting Lu, Ruoqi Zhang, Huiqi Wang, "The adaptive bearing fault diagnosis based on optimal regulation of generalized SR behaviors in fluctuating-damping induced harmonic oscillator", Mechanical Systems and Signal Processing，volume 189, 2023, 110078, 0888-3270, doi: https://doi.org/10.1016/j.ymssp.2022.110078.（这篇文献的理论部分写得很详细，实验以及对比实验也很多，等不及博客，但是想了解广义随机共振的，可以先去看看这篇\~）
二. 随机共振
1. 什么是随机共振
传统观念中噪声是有害的，需要被去除（也就是常见的去噪操作，比如各种常见的滤波器）。随机共振则表示在特定的非线性系统中，**适量的噪声不仅不会损害信号，反而能够显著增强微弱信号的检测效果。**这一现象最初在物理学研究中被发现，后来在生物系统中被广泛观察到，并逐渐发展为一种重要的信号处理技术。
Fauve 和 Heslot 等**[1]** 在1983年研究 Schmitt 触发器电路时观察到了 SR 现象。他们的实验结果显示，系统输出的信噪比 随着噪声强度 的增加而出现峰值，表现出非单调性行为。
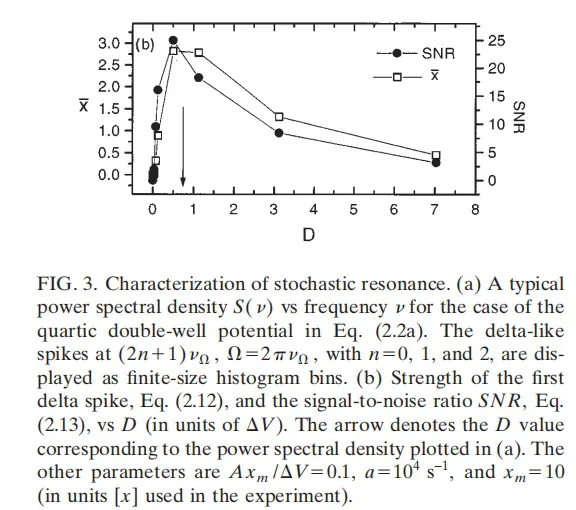
横轴D表示噪声强度，纵轴SNR表示信号与噪声的比值。这个曲线告诉我们一个反直觉的事实：并不是噪声越小越好，而是存在一个最优的噪声强度值**【2】****。**
2. 随机共振理论
2.1 基本数学模型
随机共振系统可用Langevin方程描述：
|---------|------|--------------|------|
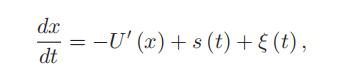
| x | U(x) | s(t) | ξ(t) |
| 布朗粒子的轨迹 | 势能函数 | 外部驱动力 （输入信号） | 噪声 |
此时x(t)也可当作是输出信号.
（可以把这个系统当成一个"滤波器"，只不过这个"滤波器"不过滤信号中的噪声，而是增加一定的噪声，是的信号中某些弱特征可以被增强.)
不过，随机共振是在一定的非线性条件下，由弱周期信号和噪声共同作用下使得非线性系统增强周期性输出。所以，如果输入的信号如果是变速信号，即非周期信号，不能直接使用随机共振系统，需要先将非周期信号通过预处理变为周期信号，比如阶次跟踪，可以将时域信号转变为角域信号。【可以下下一次讲讲阶次跟踪，也是很厉害的方法！！！】
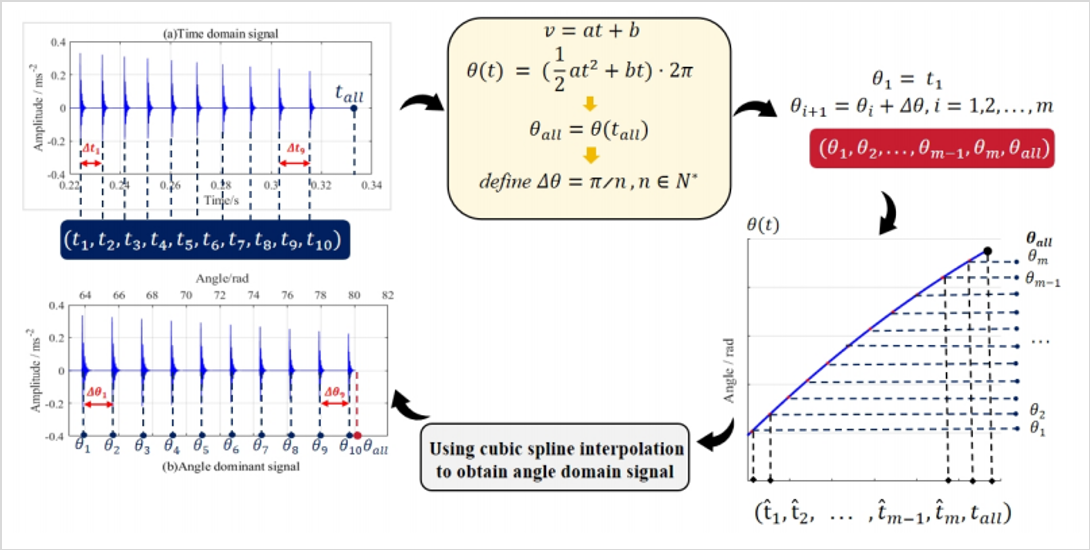我自己画的！！！！！ 不要盗图！！！画图不易！！！
2.2 常见随机共振系统
2.2节这几个系统介绍，均来自文献**【3】****。**
（看着这个阈值系统是不是也很熟悉呀~~~和神经网络中的激活函数长得很像哦~~目前也有文献用这个阈值系统当做新的激活函数~~）
综上呢，有很多随机共振系统，而且随机共振可以用在工业信号故障诊断方向，可以用在图像处理方向，计算机神经网络改进方向，以及最近的生物应用方向。
3. 文献 [4] 中随机共振的数值实现
3.1 其他创新的双稳态势阱结构
文献 [4] 中提出的是非对称双稳态系统（也有很多其他的系统，对称双稳态、三稳态、Duffing等等）
3.2 四阶Runge-Kutta方法
通过上面的四阶Runge-Kutta方法可以解出输出信号x(t)的离散表达形式进而得到输出信号。
具体的迭代过程：首先计算四个中间量k_1到k_4，它们分别对应不同时间点的斜率信息，然后通过加权平均得到下一时刻的系统状态。计算步长h的选择对精度至关重要，文献中采用h=0.1的设置在精度和计算效率之间取得了良好的平衡。
现在怎么判断输出信号是否合适呢？
随机共振主要是以信噪比（SNR）为指标。如果我们事先知道输入信号中的噪声强度，就可以通过调节系统参数a和b来改变SNR曲线的形状，使系统的最优噪声强度恰好匹配输入信号的实际噪声水平，从而实现最大化的能量转换效率。
但是在实际的生物医学信号处理中，噪声强度是不可控且难以预知的。脑电信号中的噪声来源复杂多样，包括肌电干扰、眼电干扰、设备噪声、环境干扰等，这些噪声的强度和特性在不同患者、不同时间、不同环境下都会发生变化。
（所以在生物中应用会稍微难一丢丢）
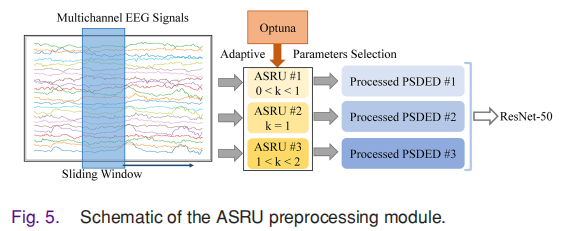
3.3 使用Optuna算法自动优化参数
由于系统参数（如势阱形状参数a、b和非对称参数A、B）的选择直接影响共振效果，研究者采用了Optuna优化算法来自动寻找最优参数组合，以系统的癫痫检测敏感性作为优化目标。
研究者选择了Optuna，这个优化过程会将整个癫痫预测流程的敏感性作为优化目标作为优化目标，那么算法会寻找能够最大化癫痫检测准确率的ASRU参数组合。这种优化策略确保了参数设置直接服务于最终的应用目标，而不是仅仅优化中间的技术指标。
