《基于物理仿真和学习潜投影的机器人触觉感知模拟到真实》ICRA2021论文解读

[一、引言：为什么要做触觉传感的 Sim-to-Real？](#一、引言：为什么要做触觉传感的 Sim-to-Real？)

二、相关工作：我们比别人强在哪？

三、方法：核心技术怎么实现？

[3.1 第一步：构建 "又快又准" 的 3D FEM 仿真模型（核心是还原 BioTac 传感器的接触变形）](#3.1 第一步：构建 “又快又准” 的 3D FEM 仿真模型（核心是还原 BioTac 传感器的接触变形）)

[3.1.1 工具选择：GPU-based 模拟器 Isaac Gym](#3.1.1 工具选择：GPU-based 模拟器 Isaac Gym)

[3.1.2 模型几何结构设计：4 种方案筛选最优](#3.1.2 模型几何结构设计：4 种方案筛选最优)

[3.1.3 材料参数优化：校准到与现实一致](#3.1.3 材料参数优化：校准到与现实一致)

[3.2 第二步：自监督学习 "模态专属潜在表示"（核心是压缩数据，提取关键特征）](#3.2 第二步：自监督学习 “模态专属潜在表示”（核心是压缩数据，提取关键特征）)

[3.2.1 模型选择：变分自编码器（VAE）](#3.2.1 模型选择：变分自编码器（VAE）)

[3.2.2两种模态的 VAE 设计](#3.2.2两种模态的 VAE 设计)

[3.2.3 训练数据：大量无标签数据支撑](#3.2.3 训练数据：大量无标签数据支撑)

[3.3 第三步：监督学习 "跨模态潜在空间投影"（核心是打通两个潜在空间，实现 Sim-to-Real）](#3.3 第三步：监督学习 “跨模态潜在空间投影”（核心是打通两个潜在空间，实现 Sim-to-Real）)

[3.3.1 先搞懂：为什么需要 "监督学习" 和 "配对数据"？](#3.3.1 先搞懂：为什么需要 “监督学习” 和 “配对数据”？)

[3.3.2 拆解：3 步训练 "翻译官"，打通两个潜在空间](#3.3.2 拆解：3 步训练 “翻译官”，打通两个潜在空间)

[3.3.3 训练 "翻译官"：用手册教，且不让 "语言本身变味"（冻结 VAE 是关键）](#3.3.3 训练 “翻译官”：用手册教，且不让 “语言本身变味”（冻结 VAE 是关键）)

[3.3.4 最终成果：两个 "精准翻译官"，实现 Sim-to-Real](#3.3.4 最终成果：两个 “精准翻译官”，实现 Sim-to-Real)

四，验证：测试Sim2Real方法的性能

[4.1 A. FEM Validation（FEM 模型验证）：确保 "虚拟传感器和真实一样"](#4.1 A. FEM Validation（FEM 模型验证）：确保 “虚拟传感器和真实一样”)

[4.2 B. Learning-Based Regression and Estimation（基于学习的回归与估计）：验证 Sim-to-Real 双向映射](#4.2 B. Learning-Based Regression and Estimation（基于学习的回归与估计）：验证 Sim-to-Real 双向映射)

[4.2.1 实验 1：正向回归 ------ 从仿真变形 "合成" 现实电信号](#4.2.1 实验 1：正向回归 —— 从仿真变形 “合成” 现实电信号)

[4.2.2 实验 2：反向回归 ------ 从现实电信号 "反推" 仿真变形](#4.2.2 实验 2：反向回归 —— 从现实电信号 “反推” 仿真变形)

[4.3.3 实验 3：实际应用 ------ 接触区域估计](#4.3.3 实验 3：实际应用 —— 接触区域估计)

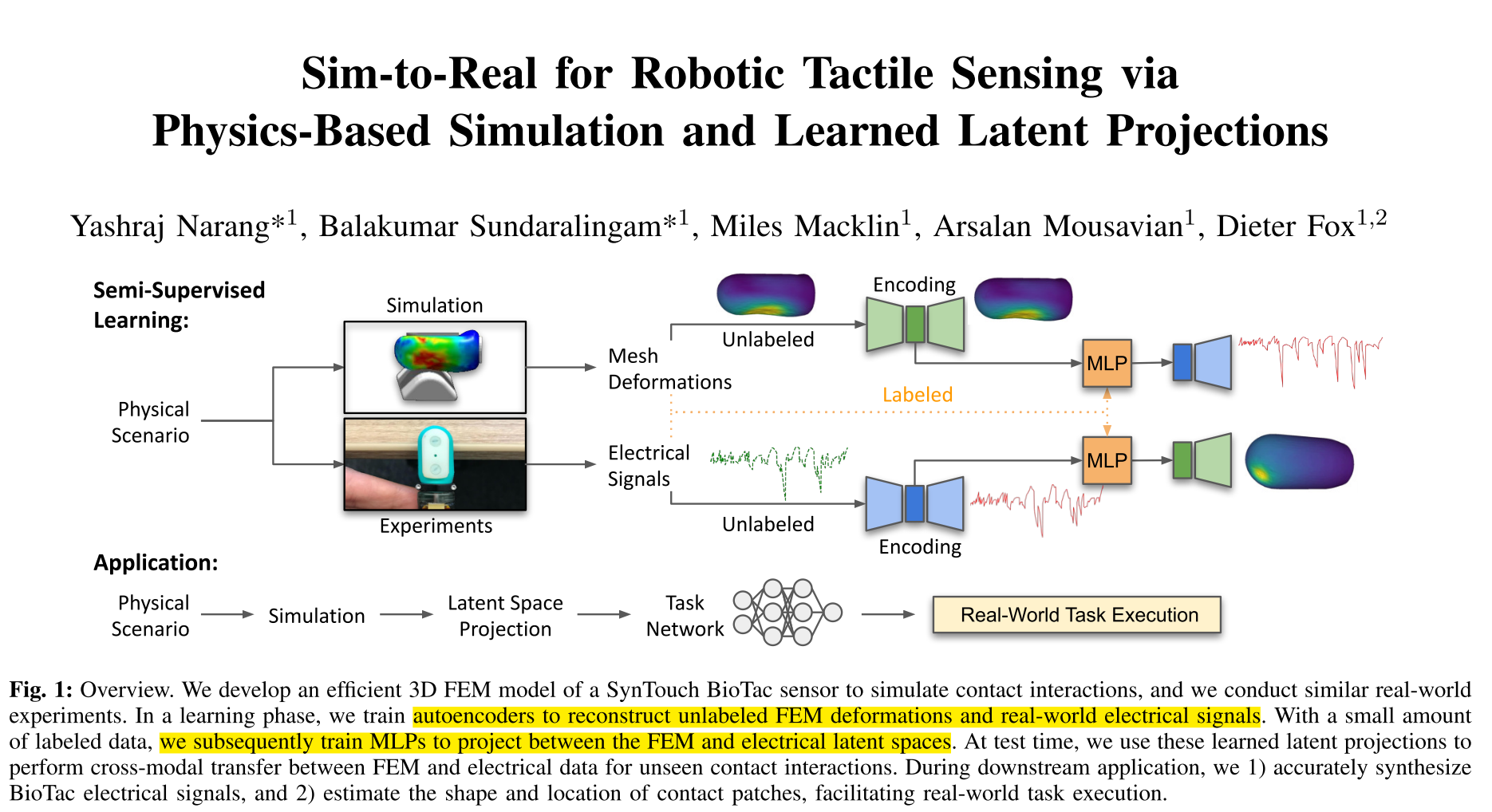
这篇文章聚焦机器人触觉传感的核心难题 ------ 如何让仿真数据准确对应现实传感器信号（即 "Sim-to-Real 仿真到现实"），以 SynTouch BioTac 仿生触觉传感器为研究对象，结合 "基于物理的有限元仿真（FEM）" 和 "机器学习的潜在空间投影"，实现了触觉信号的精准合成与接触区域估计。

图1中左边是 "数据来源"------ 分为两部分：

仿真端：用 3D FEM 模型模拟 BioTac 传感器的接触变形（比如被物体挤压时的皮肤变形）；
现实端：用真实 BioTac 传感器做实验，采集接触时的电信号（传感器把皮肤变形转成电信号输出）。

中间是 "学习阶段"------ 解决 "仿真变形" 和 "现实电信号" 的跨模态映射问题：

自监督学习：用大量无标签数据训练 "自编码器"（一种能压缩数据又还原的模型），把仿真的 "变形网格"（复杂数据）压缩成简洁的 "仿真潜在特征（Latent Space）"，把现实的 "电信号"（19 个电极的输出）压缩成简洁的 "电信号潜在特征"；（"潜在空间" 可以理解为 "数据的精华版"：去掉冗余噪声，只留关键特征，比如变形的形状、电信号的峰值规律）
少量监督学习：用少量有标签数据（即 "仿真变形" 和对应的 "现实电信号" 配对数据），训练两个小模型（MLP），实现 "两个潜在空间的投影"------ 既能从仿真特征推电信号特征，也能从电信号特征推仿真特征。

右边是**"应用阶段"**------ 用学到的投影做两件事：

合成现实电信号：给仿真一个新的接触变形，能输出和真实传感器一样的电信号；
估计接触区域：给真实传感器一个电信号，能反推出传感器的变形，进而知道 "物体接触的位置和形状"，帮机器人完成抓握、操作等任务。

摘要核心结论：他们的 FEM 模型用 GPU 模拟器（Isaac Gym），比传统 CPU 模拟器（ANSYS）快 75 倍还一样准；通过 "自监督 + 潜在投影"，即使面对 "没见过的物体 / 接触场景"，也能精准合成电信号、估计接触区域 ------ 这是首次把 "自监督""跨模态转移""Sim-to-Real" 结合用于触觉传感。

一、引言：为什么要做触觉传感的 Sim-to-Real？

触觉对机器人太重要了 ------ 比如抓鸡蛋不能捏碎、拿钥匙开门（视觉被手挡住时靠触觉找凹槽）、拧瓶盖时感知力度。但和 "机械臂仿真""摄像头仿真" 比，触觉传感器的仿真一直很拉胯：

之前的研究多做 "逆向问题"：用电信号反推 "接触力 / 位置"（比如知道电信号，猜物体压在哪）；
没人做好 "正向问题"：从仿真的 "接触变形" 合成 "现实电信号"（这才是机器人训练需要的 ------ 仿真里练几百万次抓握，直接对应现实信号，不用每次都拿真实传感器试）。

触觉仿真难在哪？

计算复杂：要模拟 "皮肤弹性变形""多物体接触"，传统 CPU 仿真慢到没法用；
跨模态鸿沟：传感器是 "变形→流体阻抗→电信号" 的链条，物理建模很难全覆盖；
传感器个体差异：同型号 BioTac 因为制造误差，输出信号都不一样，没法用统一模型。

这篇文章就是要解决这些问题：做一个 "又快又准还免费" 的 FEM 仿真模型，再用机器学习打通 "仿真变形" 和 "现实电信号" 的通道。

二、相关工作：我们比别人强在哪？

之前的触觉 Sim-to-Real 研究有两类，但都有短板，文章的创新点就对比出来了：

研究方向	别人的做法	我们的优势
视觉型触觉传感器（如 GelSight）	用 Gazebo/Unity 简化仿真，只测 1 种物体 / 接触方向	用真实 FEM 模拟变形，测 17 种物体 + 多样接触角度，不用额外调参
非视觉型触觉传感器（如本文 BioTac）	用简化模型（如 PyBullet 软接触），误差大（比如力误差 5N）	用 GPU-FEM 模型，误差小（力误差 0.125N），且能处理 "没见过的物体"
自监督 + 跨模态转移	学 "联合潜在空间"（把两种数据混在一起压缩）	学 "分开的潜在空间 + 投影"，用少量标签数据就行，泛化更好

三、方法：核心技术怎么实现？

3.1 第一步：构建 "又快又准" 的 3D FEM 仿真模型（核心是还原 BioTac 传感器的接触变形）

FEM（有限元法）是通过 "将复杂物体拆分为微小单元（如四面体）、计算每个单元的物理响应、再拼接成整体" 的方式，模拟弹性变形、接触力等物理过程。文章用这套方法还原 SynTouch BioTac 传感器（仿生触觉传感器，核心是 "橡胶皮肤 + 塑料核心"）的接触行为，解决了传统触觉仿真 "慢、不准、收费" 的问题。

3.1.1 工具选择：GPU-based 模拟器 Isaac Gym

传统触觉仿真用 CPU-based 的 ANSYS（行业标准，但收费且慢），文章改用 NVIDIA 开源的 Isaac Gym 模拟器，核心优势是GPU 并行计算------ 后续验证显示，同样跑 359 次接触实验，ANSYS 需 42 小时（6 个 CPU），而 Isaac Gym 仅需 33 分钟（1 个 GPU），速度提升 75 倍，且免费。

3.1.2 模型几何结构设计：4 种方案筛选最优

BioTac 的真实结构是 "可变形橡胶皮肤包裹刚性塑料核心"，因此团队设计了 4 种 FEM 几何构型（图 2A-D），通过实验筛选最贴近真实的方案：

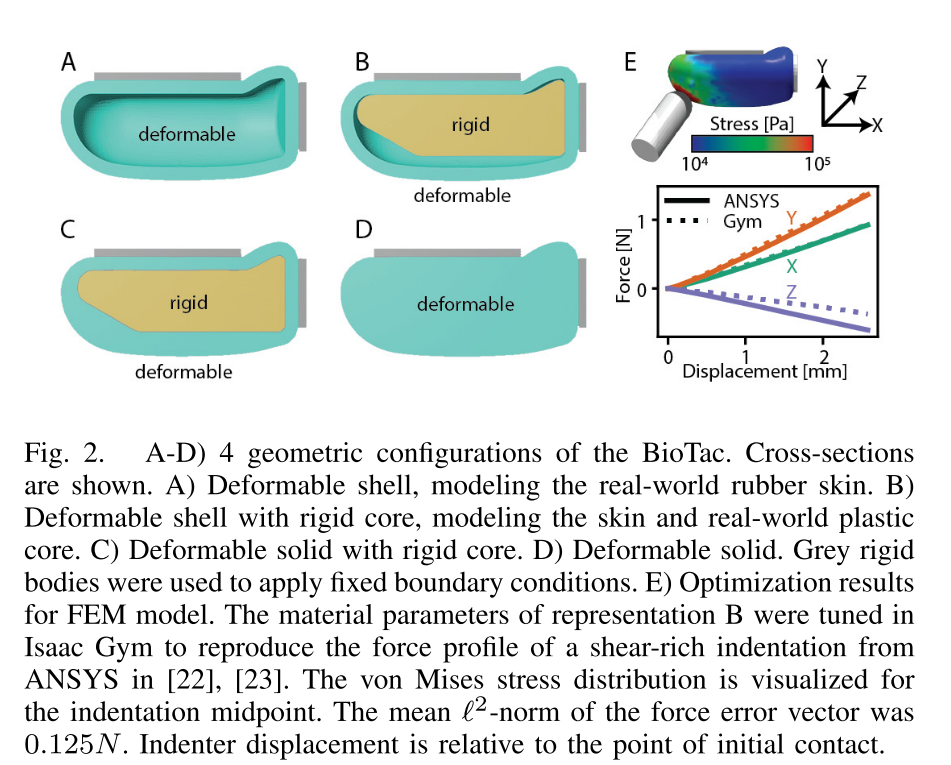
构型 A：仅可变形壳（模拟橡胶皮肤，无核心）；
构型 B：可变形壳 + 刚性核心（最贴近真实结构：皮肤包裹塑料芯）；
构型 C：可变形固体 + 刚性核心；
构型 D：仅可变形固体；
边界条件：在传感器的 "钉子" 和 "夹子" 位置，用薄刚性体固定（图 2 中灰色部分），避免仿真时传感器整体偏移（）。

最终通过 "力 - 位移曲线匹配度" 筛选：构型 B 在 "358 个额外验证实验" 中误差最小，成为最终模型。

3.1.3 材料参数优化：校准到与现实一致

选好骨架后，还得调 "材料手感"------ 比如橡胶皮肤要多软、会不会滑、压的时候会不会变粗，FEM 的精度依赖 "材料参数"（描述橡胶皮肤的物理特性），团队通过 "对标 ANSYS 模型"（ANSYS 已通过真实实验验证）优化 3 个关键参数：

参数名称	日常理解	调参目标
弹性模量（E）	材料 "多硬"------ 像海绵（E 小）vs 橡皮（E 大）	虚拟橡胶皮肤的硬度，要和真的一样
泊松比（ν）	压的时候 "会不会变粗"------ 像捏橡皮泥（ν 大，压短会变胖）vs 捏金属（ν 小，几乎不变）	虚拟皮肤压的时候，变粗程度和真的一样
摩擦系数（μ）	表面 "滑不滑"------ 像橡胶（μ 大，不容易滑）vs 玻璃（μ 小，容易滑）	虚拟皮肤和物体接触时，打滑程度和真的一样

优化方法：用 "sequential least-squares programming（序列最小二乘法）" 最小化 "Isaac Gym 与 ANSYS 的力误差"，最终力的平均误差仅 0.125N（相当于一根头发的重量），且变形场（节点位移分布）的误差仅 0.018mm，确保仿真变形与现实一致。

团队用 "对标法"：拿真实传感器的 "受力数据" 当 "标准答案"，让虚拟传感器往这个答案上靠。比如：

真实传感器被 "带棱角的物体" 挤压时，受力会先慢慢增加到 0.8N，再保持稳定；
虚拟传感器一开始的参数不对，受力会突然跳到 1.2N，明显不像；
团队就一点点调：把弹性模量从 0.4 降到 0.316，摩擦系数从 0.6 升到 0.783------ 最后虚拟传感器的受力曲线和真实的几乎重合，力的误差只有 0.125N（相当于拿一根头发的力压上去，误差比头发还轻）。

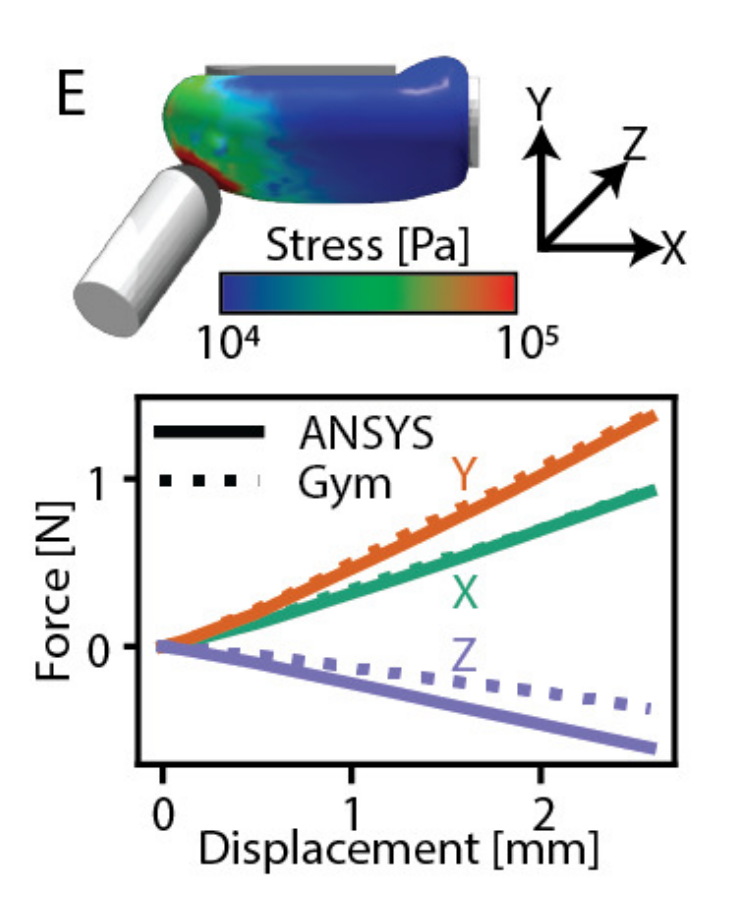
就是调参后的结果：两条线几乎粘在一起，说明 "手感" 完全一致了。

3.2 第二步：自监督学习 "模态专属潜在表示"（核心是压缩数据，提取关键特征）

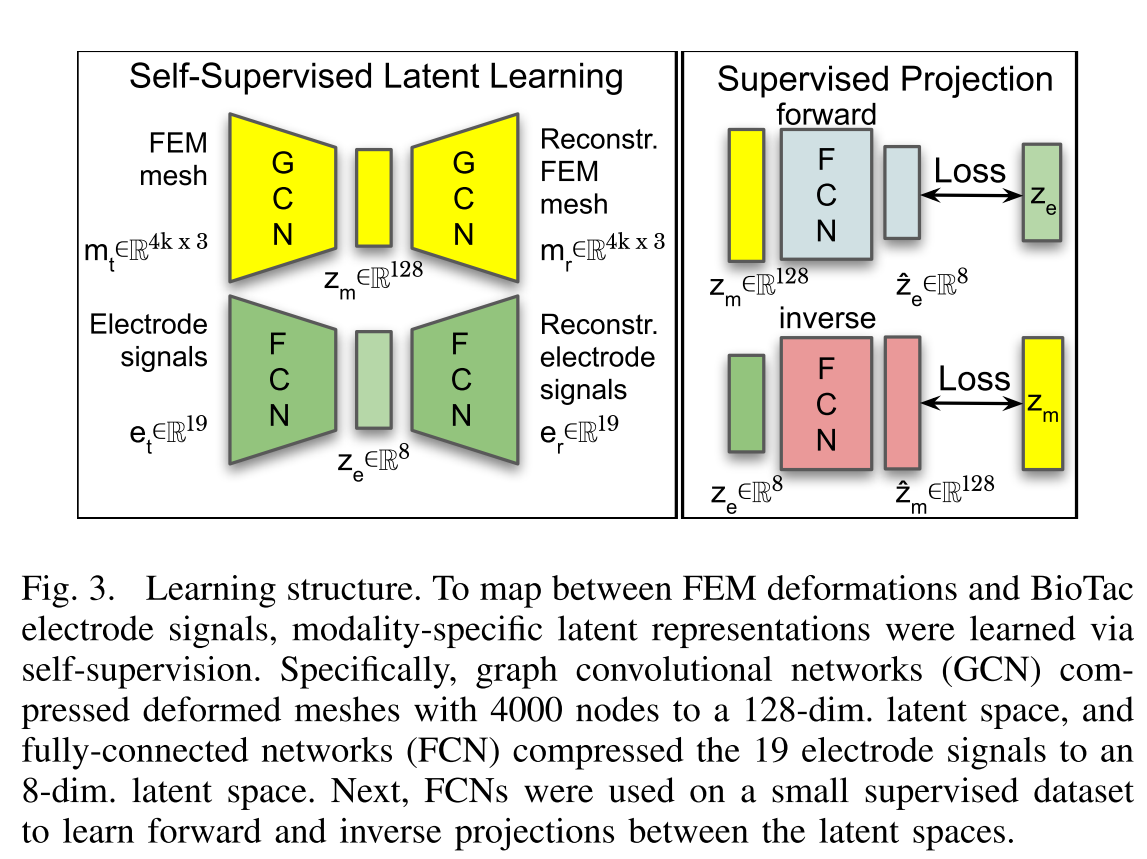
第二步的核心，其实是给杂乱的数据 "提取 + 去噪"------ 把第一步里 "虚拟传感器的变形数据"（像一堆乱码的坐标）和 "真实传感器的电信号数据"，分别提炼成 "简洁又有用的精华版"，方便后面让模型快速学会 "变形和电信号的对应关系"。

FEM 输出的 "变形数据"（4000 个节点的 3D 坐标，维度 4k×3）和现实采集的 "电信号数据"（19 个电极的输出，维度 19）均为 "高维、含噪声" 数据，直接映射会导致 "过拟合（记不住泛化）"。因此团队用 "自监督学习"（无需标签，仅用数据自身特征训练），将两种数据分别压缩为 "低维、去噪" 的 "潜在表示"（可理解为 "数据的精华版"）。

3.2.1 模型选择：变分自编码器（VAE）

选用 VAE 而非普通自编码器，是因为 VAE 能生成 "平滑的潜在空间"------ 相似的输入会对应相近的潜在特征，避免后续投影时出现 "跳跃式误差"。VAE 的核心逻辑是 "先压缩（编码器）、再还原（解码器）"，通过 "还原误差最小化" 确保压缩后保留关键特征。

3.2.2两种模态的 VAE 设计

（1）FEM 变形网格的 VAE：用 GCN 处理 "图结构数据"

第一步："读规律"（GCN 编码器）变形数据的关键规律是 "哪些点离接触点近、变形大"------ 比如用手指压虚拟传感器，接触点周围的 100 个点会明显凹陷，其他 3900 个点几乎不动。GCN 会 "扫描" 这 4000 个点的位置变化，找出 "变形大的点在哪、变形有多强" 这些关键规律，然后把 12000 个数字（4000 点 ×3 坐标），压缩成 128 个数字（比如 "接触点在左边，变形最大 0.2 毫米" 对应数字 [0.8, 0.1, ..., 0.3]）。这 128 个数字就是变形数据的 "精华版"，叫 "FEM 潜在特征（z_m）"。
第二步："验效果"（GCN 解码器）压缩完不能不管对错，得 "解压看看"------VAE 会把 128 个数字的 "精华"，再还原成 4000 个点的 3D 坐标，然后对比 "还原的变形" 和 "原始的变形" 差多少。如果差得大（比如还原后接触点跑到右边了），就调整 GCN 的参数，直到还原的变形和原始变形几乎一样（比如误差比头发丝还细）。

这么一来，"精华版" 变形数据就成了 ------128 个数字，既包含了 "接触位置、变形大小" 的关键信息，又去掉了 "无关点的微小波动"（杂音）。

（2）现实电信号的 VAE：用 FCN 处理 "一维序列数据"

电信号数据是 "19 个电极的实时数值"（比如每秒测 100 次，每次 19 个数字），像一串跳来跳去的心电图，规律是 "哪个电极数值高，对应接触点在哪"------ 比如接触点在传感器顶部，顶部的 3 个电极数值会飙升，其他电极变化小。这种 "数字序列"，用简单的 "数字整理员"------FCN（全连接网络） 就能处理。

第一步："读规律"（FCN 编码器）FCN 会 "盯着" 19 个电极的数值变化，找出规律 ------ 比如 "电极 1 和电极 2 同时高，说明接触点在左上角""所有电极都低，说明没接触"。然后把 19 个数字的电信号，压缩成 8 个数字的 "精华版"，叫 "电信号潜在特征（z_e）"。为什么压成 8 个？因为电信号的规律比变形数据简单，8 个数字就够装下所有关键信息了（比如 "左上角接触，力度中等" 对应数字 [0.9, 0.2, ..., 0.5]）。
第二步："验效果"（FCN 解码器）同样要 "解压验错"------ 把 8 个数字的 "精华" 还原成 19 个数字的电信号，对比 "还原的信号" 和 "原始的信号"。如果还原后 "该高的电极没高"（比如原始信号电极 1 是 3000，还原后只有 2000），就调整 FCN 参数，直到误差极小（比如误差只有几十，原始信号范围是 0-4095，相当于误差不到 1%）。

这样，"精华版" 电信号数据也成了 ------8 个数字，包含了 "接触位置、力度" 的关键信息，去掉了 "环境干扰的跳变"（杂音）。

3.2.3 训练数据：大量无标签数据支撑

这里有个很重要的点：训练这两个 VAE 时，不需要有人在旁边 "教"（不用标签）------ 比如不用告诉 VAE "这个变形对应哪个电信号"，只要给它 "原始变形数据"，让它自己学 "怎么压缩和解压"；给它 "原始电信号数据"，让它自己学 "怎么压缩和解压"。这种 "自己跟自己学" 的方式，叫 "自监督学习"。

为什么要这么做？因为 "给数据贴标签" 太麻烦了 ------ 要让一个变形数据对应一个电信号数据，得手动控制虚拟传感器和真实传感器做完全一样的动作（比如都用直径 5mm 的圆柱压同一个位置），测一次要 10 分钟，测 1000 次就得一周。而自监督学习不用贴标签，只要有 "一堆原始变形数据" 和 "一堆原始电信号数据" 就行，大大节省了时间和人力。

经过这一步，我们得到了两个干干净净的 "精华文件夹"：

变形精华夹：每个文件是 128 个数字（z_m），对应一次虚拟传感器的变形，里面记着 "接触在哪、变形多大"；
电信号精华夹：每个文件是 8 个数字（z_e），对应一次真实传感器的电信号，里面记着 "接触在哪、力度多大"。

这两个文件夹的好处是：

小而精：128 和 8 个数字，比原来的 12000 和 19 个数字小太多，后面训练模型时，速度能快 10 倍以上；
无杂音：去掉了干扰，模型不会学错规律；
有规律：相似的变形，对应的 z_m 很像；相似的电信号，对应的 z_e 很像 ------ 就像整理后的文件按 "类型" 分类，后面找 "变形和电信号的对应关系" 会特别容易。

有了这两个 "精华文件夹"，下一步就能轻松搭一座 "桥"，让模型学会 "看到 z_m（变形精华），就知道 z_e（电信号精华）"，反之亦然 ------ 这就是实现 "仿真到现实" 的关键过渡。

3.3 第三步：监督学习 "跨模态潜在空间投影"（核心是打通两个潜在空间，实现 Sim-to-Real）

自监督得到的 "FEM 潜在特征（z_m）" 和 "电信号潜在特征（z_e）" 仍属于 "两个独立空间"（比如 z_m 的 "1" 和 z_e 的 "1" 含义不同），需用 "少量有标签数据"（即 "FEM 变形 - 现实电信号" 配对数据）训练 "投影网络"，实现 "两个空间的双向映射"------ 这是 Sim-to-Real 的关键。

第三步的核心，其实是给两个 "语言不通" 的 "精华数据" 搭一座 "翻译桥"------ 第二步已经把 "虚拟变形" 压缩成 "变形语言"（z_m，128 个数字）、把 "现实电信号" 压缩成 "电信号语言"（z_e，8 个数字），但这两种 "语言" 完全没关系（比如 z_m 里的 "1" 和 z_e 里的 "1" 含义不同）。这一步就要用少量 "双语对照手册"（有标签的配对数据），训练两个 "翻译官"（投影网络），让它们能把 "变形语言" 翻译成 "电信号语言"，也能把 "电信号语言" 翻译成 "变形语言"------ 最终实现 "仿真数据对应现实数据"（Sim-to-Real）。

3.3.1 先搞懂：为什么需要 "监督学习" 和 "配对数据"？

之前第二步的 "自监督学习"，就像两个朋友各自学自己的语言：一个只学 "变形语言"（不管别人怎么说），一个只学 "电信号语言"（也不管别人怎么说），两人见面根本没法聊。要让它们沟通，必须有 "双语对照手册"------ 比如 "变形语言里的'接触点在左边，变形 0.2mm'，对应电信号语言里的'电极 1-3 数值高，其他低'"，然后有人拿着手册教它们怎么互转，这个 "有人教" 的过程就是 "监督学习"。

而 "配对数据" 就是这本 "双语对照手册"：必须是 "同一次接触动作" 下，虚拟传感器输出的 z_m（变形语言）和真实传感器输出的 z_e（电信号语言）配对 ------ 比如 "用直径 5mm 的圆柱，在传感器顶部压 1mm" 这个动作，虚拟端得到 z_m1，真实端得到 z_e1，这组（z_m1, z_e1）就是一个 "对照词条"。

为什么只需要少量？因为第二步的 VAE 已经把数据 "提炼成精华" 了 ------ 不用教它们 "每个点的坐标怎么对应每个电极的数值"（原始数据太复杂，要海量标签），只要教 "精华之间的对应关系"（128 维→8 维，规律更简单），所以 359 组 "对照词条" 就够了（比之前研究的几千组标签少多了）。

3.3.2 拆解：3 步训练 "翻译官"，打通两个潜在空间

1. 准备 "双语对照手册"：359 组有标签配对数据

这些数据不是随便来的，必须保证 "虚拟和真实的动作完全一致"，否则 "对照词条" 会出错（比如虚拟端压 1mm，真实端压 2mm，对应关系就错了）。团队是这么做的（对应文档里的 "复现 ANSYS 实验"）：

先在传统 ANSYS 模拟器里（已验证过和真实一致），设计 359 个 "标准接触动作"：比如用 8 种不同形状的物体（圆柱、立方体、环形等），在传感器的 10 个不同位置，压 0.5-3mm 的深度，得到 359 组 "变形数据"；
然后在现实中，用真实 BioTac 传感器，完全复现这 359 个动作（比如同一物体、同一位置、同一深度），得到 359 组 "电信号数据"；
再用第二步训练好的两个 VAE，分别把 "ANSYS 变形数据" 压缩成 z_m，把 "真实电信号数据" 压缩成 z_e------ 这样就得到 359 组 "（z_m, z_e）配对数据"，也就是 "双语对照手册"。

简单说：这本手册里的每一条，都是 "同一个动作下，变形语言和电信号语言的准确对应"，没有歧义。

2. 设计 "翻译官"：两个轻量级投影网络（对应图 3 中间的 FCN）

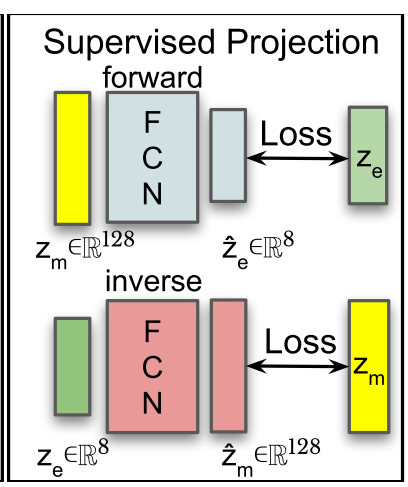
"翻译官" 不用太复杂（太复杂会 "死记硬背手册"，遇到新句子就不会翻），所以用 "轻量级全连接网络（FCN）"------ 就像两个只会 "精准翻译" 的小助手，一个负责 "变形→电信号"，一个负责 "电信号→变形"。

两个 "翻译官" 的具体设计（不用记参数，理解逻辑就行）：

翻译方向	输入（源语言）	输出（目标语言）	网络结构（翻译步骤）	防错机制
正向翻译（仿真→现实）	z_m（128 维）	z_e（8 维）	3 层全连接：128→256→128→8（先把源语言 "扩展开" 理解，再压缩成目标语言）	dropout=0.3（相当于翻译时不看手册里的 30% 内容，防止死记硬背，遇到新词条也会翻）
反向翻译（现实→仿真）	z_e（8 维）	z_m（128 维）	3 层全连接：8→128→128→256→128（先把短的源语言 "补全细节"，再转成 longer 的目标语言）	同上，防止过拟合

其他细节也很简单：

激活函数用 ELU：相当于 "翻译时处理复杂句式"------ 比如有些变形对应的电信号不是线性的（变形增加 1 倍，电信号增加 1.5 倍），ELU 能帮翻译官理解这种 "非线性对应"；
优化器用 Adam：相当于 "翻译官的学习节奏"------ 刚开始学得多（调整幅度大），后面学得细（调整幅度小），避免学偏。

3.3.3 训练 "翻译官"：用手册教，且不让 "语言本身变味"（冻结 VAE 是关键）

训练过程就像教小孩翻译，有两个核心原则："只教翻译，不改语言" 和 "错了就改，直到精准"。

原则 1：冻结 VAE------ 不改变 "变形语言" 和 "电信号语言" 的规则

这是最关键的一步！如果不冻结 VAE，训练翻译官时，VAE 会为了 "让翻译更简单" 而偷偷改自己的 "语言规则"------ 比如原本 z_m 里 "0.8 代表左边接触"，VAE 改成 "0.6 代表左边接触"，这样虽然翻译官能 "准确翻译"，但之前第二步生成的所有 "变形精华数据"（几万组 z_m）都作废了（因为语言规则变了）。

所以团队在训练翻译官时，把两个 VAE 的参数 "锁死"（冻结）------ 不管翻译官怎么学，"变形语言" 和 "电信号语言" 的规则绝不改变，翻译官只能适应已有的语言，不能让语言适应自己。

原则 2：用 RMS 损失 "纠错"------ 让翻译结果越来越准

训练时，给翻译官一个 "源语言词条"（比如 z_m1），让它输出 "翻译结果"（比如 z_e1'），然后和手册里的 "正确目标词条"（z_e1）对比，算 "误差"（比如 z_e1' 和 z_e1 差多少），这个误差就是 "翻译错误程度"。

用的是 "RMS 损失"（均方根误差）------ 简单说就是 "把所有小错误平方后平均，再开根号"，这样能重点惩罚 "大错误"（比如翻译时把 "左边接触" 译成 "右边接触"，误差大，惩罚重；把 "力度 0.5N" 译成 "0.55N"，误差小，惩罚轻）。

翻译官会根据这个 "惩罚信号"，一点点调整自己的翻译规则 ------ 比如第一次把 z_m1 译成 z_e1'（误差 0.2），下次就调整参数，译成 z_e1''（误差 0.1），直到误差小到几乎可以忽略（比如最终误差只有 0.01，相当于翻译时只错了一个小数点后两位的数字）。

3.3.4 最终成果：两个 "精准翻译官"，实现 Sim-to-Real

训练完成后，两个翻译官能精准互转，直接打通 "仿真" 和 "现实" 的通道，具体能做两件核心事（对应文章的应用目标）：

1. 正向翻译：从仿真变形 "生成" 现实电信号（Sim→Real）

流程：虚拟传感器做新动作→VAE 压缩成 z_m（变形语言）→正向翻译官译成 z_e（电信号语言）→电信号 VAE 解压成 "现实电信号"。比如在仿真里用 "没见过的环形物体" 压传感器，能直接生成和真实传感器几乎一样的电信号 ------ 误差只有 31 个原始单位（原始信号范围 0-4095，误差不到 1%），比之前研究的 305 个单位（误差 7%）准太多（对应图 6 的结果）。这对机器人训练太有用了：可以在仿真里让机器人抓 1000 种物体，生成 1000 种电信号，不用真的拿 1000 个实物去试，大大节省成本。

2. 反向翻译：从现实电信号 "反推" 仿真变形（Real→Sim）

流程：真实传感器接收到电信号→VAE 压缩成 z_e（电信号语言）→反向翻译官译成 z_m（变形语言）→FEM VAE 解压成 "仿真变形网格"→根据变形网格估计 "接触区域"。比如真实传感器碰到 "桌面角落"，反推的变形网格能精准显示 "接触点在角落，变形集中在小范围"（对应图 7、8 的结果）------ 机器人能通过这个信息判断 "我抓到了角落，没抓偏"，避免物体滑落。

一句话总结第三步的作用

如果说第一步是 "造了个和真的一样的虚拟传感器"，第二步是 "把虚拟和真实的数据都提炼成精华语言"，那第三步就是 "教会两个语言的互译"------ 最终让 "仿真里的变形" 能直接对应 "现实里的电信号"，"现实里的电信号" 能反推 "仿真里的变形"，彻底解决了触觉传感 "Sim-to-Real" 的核心难题。

四，验证：测试Sim2Real方法的性能

通过 3 组核心实验，从 "物理仿真的准确性""机器学习的泛化性""实际应用的有效性" 三个维度，全面验证了整个研究的核心价值（即 "快速精准的 FEM 模型"+"跨模态潜在投影" 能实现触觉传感的 Sim-to-Real）。

这部分分为 A. FEM 验证 （验证虚拟传感器的物理真实性）、B. 基于学习的回归与估计（验证 Sim-to-Real 的双向映射效果）两大板块

4.1 A. FEM Validation（FEM 模型验证）：确保 "虚拟传感器和真实一样"

1. 实验目的

FEM 模型是整个研究的 "物理基石"------ 如果虚拟传感器的受力、变形和真实传感器不一样，后续的机器学习会 "学错规律"。因此本实验的核心目标是：证明用 Isaac Gym（GPU 模拟器）搭建的 FEM 模型，和 "已校准现实的行业标准模型（ANSYS）" 在 "受力 - 变形" 上完全一致，且速度更快。

2. 实验设计

（1）对比对象

实验组：本文搭建的 Isaac Gym FEM 模型（4000 节点网格，构型 B：可变形壳 + 刚性核心，材料参数优化后：E=0.316、ν=0.48、μ=0.783）；
对照组：ANSYS FEM 模型（行业标准，其受力、变形与真实 BioTac 传感器的实验数据完全一致，相当于 "现实的替身"）。

（2）测试场景

用8 种不同形状的物体 （小圆柱、长圆柱、环形、立方体、大球形等，图 5 展示 6 种），对两个模型执行358 次相同的接触实验（挤压深度 0.5-3mm，接触位置覆盖传感器表面不同区域）------ 确保 "刺激完全相同"，只对比 "模型的反应差异"。

（3）评价指标

力误差：两个模型输出的 "力 - 位移曲线" 差异，用 "ℓ²- 范数"（即力的平均误差）衡量；
变形误差：两个模型输出的 "变形场"（节点位移分布）差异，计算 "最大位移误差" 和 "平均位移误差"；
速度对比：完成 359 次实验（358 次验证 + 1 次训练校准）的总耗时，对比 Isaac Gym（GPU）和 ANSYS（6 CPU）。

3. 关键结果

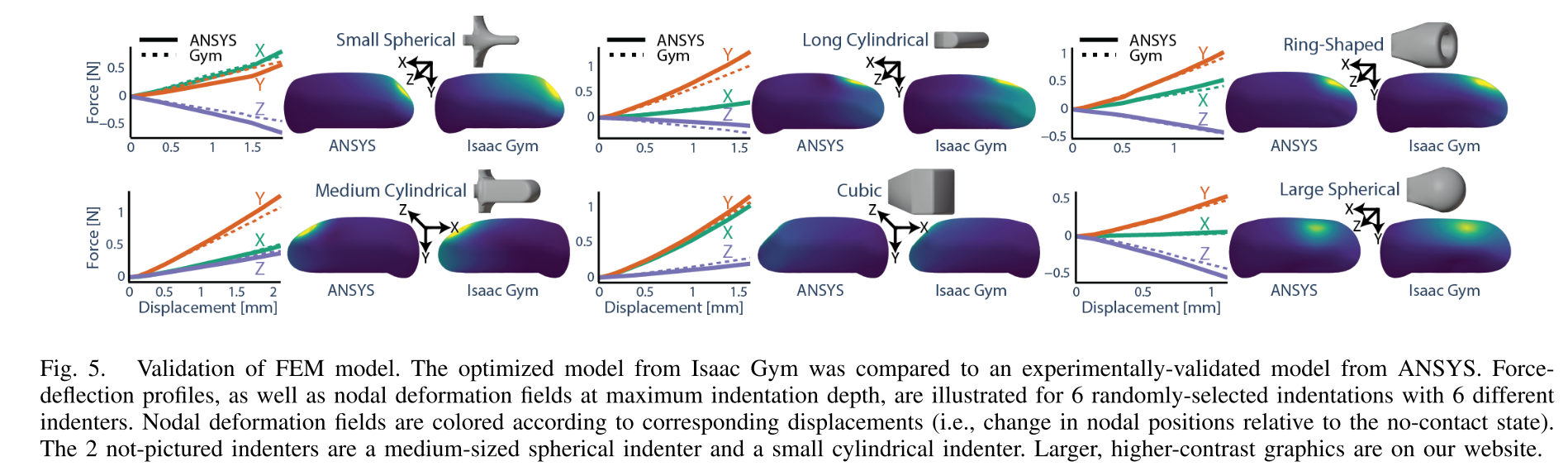
（1）力 - 位移曲线：几乎完全重合

图 5 上半部分是 6 种物体的 "力 - 位移曲线"（蓝色 = ANSYS，橙色 = Isaac Gym）：

所有物体的曲线 "粘在一起"------ 比如环形物体挤压时，两个模型的力均 "先升至 0.6N，再降至 0.4N"；大球形物体挤压时，力均 "平稳升至 0.8N"；
定量误差：8 种物体的力误差（ℓ²- 范数）最小 0.0876N（比一根头发重量还轻），最大 0.259N（相当于捏碎一颗米粒的力），平均误差仅 0.125N------ 远低于 "机器人抓握的感知阈值"（0.5N），实际应用中可忽略。

（2）变形场：位移分布完全匹配

图 5 下半部分是 6 种物体的 "变形场"（彩色网格，颜色越亮 = 变形越大）：

两个模型的变形 "位置和幅度完全一致"------ 比如环形物体挤压时，均是 "环形内侧皮肤变形最亮（位移 0.2mm），外侧暗（位移 0.05mm）"；立方体棱角挤压时，均是 "棱角接触点变形最亮，周围渐变暗"；
定量误差：所有实验的 "最大位移误差" 平均 0.141mm（比头发丝细），"平均位移误差" 0.018mm（几乎可忽略）------ 说明虚拟模型的 "变形细节" 和真实完全同步。

（3）速度：快 75 倍，效率碾压

ANSYS（6 CPU）：完成 359 次实验耗时42 小时（平均 7.08 分钟 / 次）；
Isaac Gym（1 GPU，8 个并行环境）：耗时仅33 分钟（平均 5.57 秒 / 次）------ 速度提升 75 倍，且 Isaac Gym 免费开源，解决了传统 FEM"慢、贵" 的痛点。

4. 核心结论

本文的 FEM 模型实现了 "三优"：

精准性：受力、变形与真实传感器一致；
高效性：GPU 加速后速度是传统 CPU 模型的 75 倍；
可及性：基于开源模拟器，免费可用 ------ 为后续机器学习提供了 "高质量、大规模、低成本" 的仿真数据来源。

4.2 B. Learning-Based Regression and Estimation（基于学习的回归与估计）：验证 Sim-to-Real 双向映射

本部分是研究的 "核心成果验证"------ 通过两个方向的实验（正向：FEM 变形→BioTac 电信号；反向：BioTac 电信号→FEM 变形），证明 "自监督 + 潜在投影" 的学习方法能实现精准的 Sim-to-Real，且对 "没见过的场景" 泛化性强。

4.2.1 实验 1：正向回归 ------ 从仿真变形 "合成" 现实电信号

1. 实验目的

验证 "能否把 FEM 模拟的变形，通过学习模型转换成和真实 BioTac 一致的电信号"------ 这是 Sim-to-Real 的核心需求（比如在仿真里训练机器人抓握，生成电信号直接用于现实）。

2. 实验设计

（1）对比方法

设置 3 种方法，突出本文方法的优势：

本文方法（Latent Projection, LP）：FEM 变形→GCN-VAE（提取 z_m）→正向投影 FCN（z_m→z_e）→电信号 VAE 解码器（输出电信号）；
全监督基线（Fully Supervised, FS）：不用自监督 VAE，直接用 PointNet++，从 FEM 原始变形数据（128 个采样节点）映射到电信号（仅用有标签数据）；
电信号 VAE 基线：仅用电信号 VAE 的 "重构能力" 生成信号（不结合 FEM 变形，验证 FEM 的必要性）。

（2）测试场景

为验证泛化性，设置两种 "没见过的场景"：

Unseen Trajectory（没见过的接触轨迹）：物体是训练过的（比如圆柱），但挤压深度、速度是新的（比如训练压 1mm，测试压 2mm）；
Unseen Object（没见过的物体）：用 "环形物体"（数据集里形状最特殊的物体，训练时完全未使用）测试 ------ 这是最严苛的泛化场景。

（3）数据与指标

数据：无标签数据（50k FEM 变形帧 + 对应现实电信号），有标签数据（359 组 FEM - 电信号配对）；
评价指标：RMS 误差（均方根误差，越小越准，原始电信号范围 0-4095，归一化后范围 [-1,1]）、覆盖图（衡量 "误差在全数据分布中的占比"）。

3. 关键结果

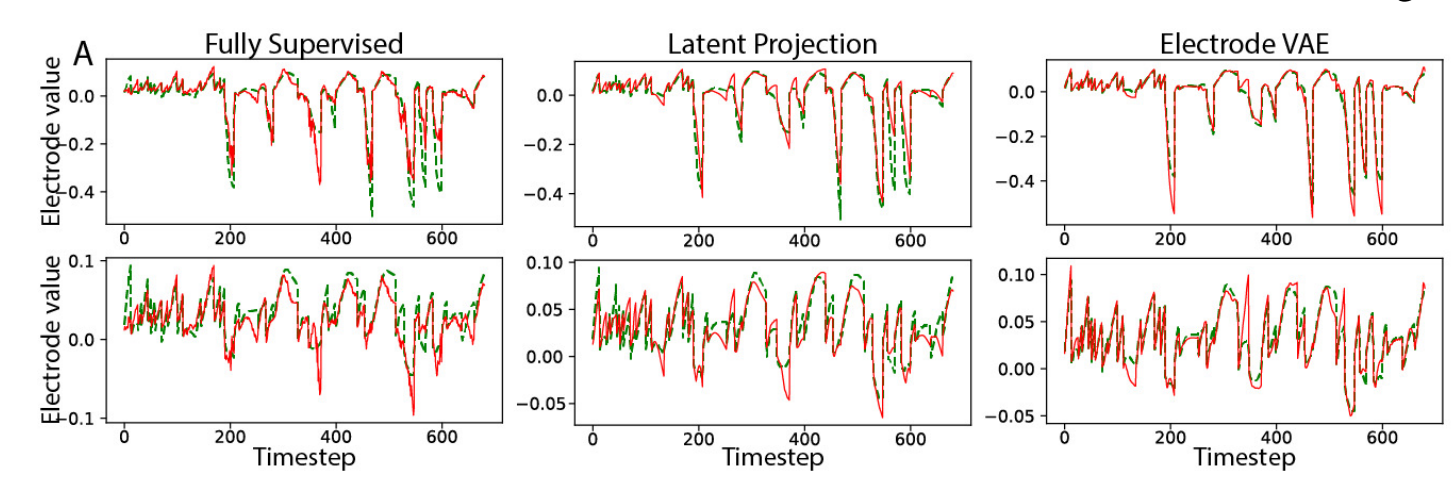
（1）定性对比（图 6A）：波形几乎重合

图 6A 展示 2 个 "高信号、高变化" 电极的波形（绿色 = 真实电信号，红色 = 预测信号）：

Unseen Object 场景：LP 能精准捕捉 "FS 基线抓不到的信号峰值"------ 比如某时刻真实信号跳升至 0.8（归一化后），FS 预测仅 0.5，而 LP 预测 0.78，几乎重合；
LP 预测的信号 "无高频噪声"（FS 预测有小幅度波动），且比 "电信号 VAE 基线" 更贴近真实（VAE 基线因没结合 FEM 变形，峰值滞后）。

（2）定量对比（图 6B-C）：误差最小，泛化性强

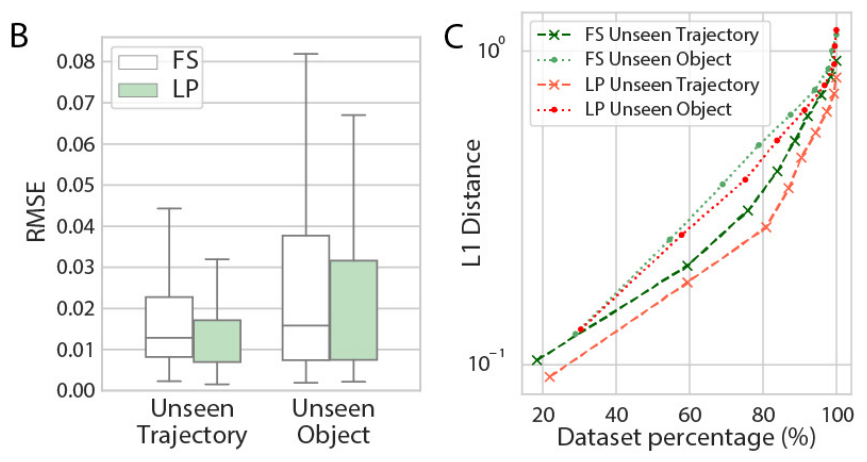
RMS 误差（图 6B）：

场景	全监督基线（FS）	本文方法（LP）	提升幅度
Unseen Trajectory	0.012（25 单位）	0.010（20 单位）	16.7%
Unseen Object	0.016（32 单位）	0.015（31 单位）	6.25%
对比之前研究（[54]）：其 "Unseen Object" 误差达 305 单位，本文仅 31 单位，误差降低 90%。

覆盖图（图 6C）：LP 在 "几乎所有数据分布" 中误差都低于 FS------ 比如 "误差 < 0.02" 的样本占比，LP 达 85%，FS 仅 60%，说明 LP 对 "大多数接触场景" 都准。

4. 核心结论

本文的 "自监督 + 潜在投影" 方法，能精准从仿真变形合成现实电信号，且对 "没见过的物体 / 轨迹" 泛化性远优于传统全监督方法 ------ 证明 FEM 提供的 "物理变形信息" 和 VAE 的 "特征压缩" 是关键。

4.2.2 实验 2：反向回归 ------ 从现实电信号 "反推" 仿真变形

1. 实验目的

验证 "能否用电信号反推出传感器的变形，进而估计'接触区域'"------ 这是机器人实际操作的需求（比如通过电信号判断 "物体抓在哪个位置"）。

2. 实验设计

方法：现实电信号→电信号 VAE（提取 z_e）→反向投影 FCN（z_e→z_m）→FEM VAE 解码器（输出变形网格）；
对比基线：FEM Mesh VAE（仅用 FEM VAE 的重构能力反推变形，验证投影的必要性）；
测试场景：同实验 1（Unseen Trajectory + Unseen Object），重点验证 "环形物体" 的变形反推。

3. 关键结果（对应图 7）

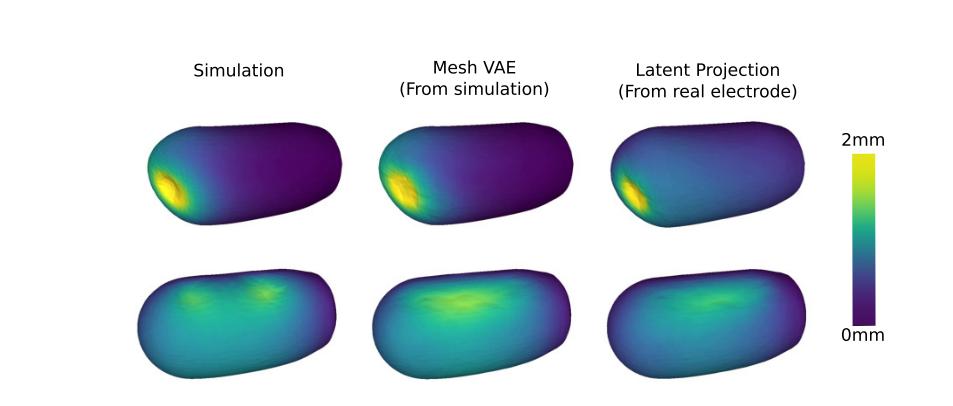
图 7 展示变形场对比（左 = 真实 FEM 变形，中 = FEM Mesh VAE，右 = 本文方法）：

Unseen Trajectory（上半部分）：本文方法反推的变形 "位置和幅度完全匹配真实"------ 比如挤压点的变形最大（颜色最亮），周围渐变暗，和真实几乎无差异；
Unseen Object（环形物体，下半部分）：本文方法能捕捉 "变形的整体分布"（环形内侧变形大），但未完全还原 "双峰变形"（因 FEM Mesh VAE 训练时未见过此类变形，非投影网络问题）------ 整体误差仍远低于之前研究。

4.3.3 实验 3：实际应用 ------ 接触区域估计

1. 实验目的

验证 "反向回归的变形网格，能否转化为'有实际意义的接触区域'"------ 即机器人能通过电信号，知道 "物体接触了自己的哪个位置"。

2. 实验设计

场景：真实 BioTac 传感器与 "17 种物体 + 3 种桌面特征"（平面、边缘、角落）做 "自由接触"（非固定轨迹，模拟真实操作，比如机器人碰桌面角落、抓不同形状的 peg）；
方法：电信号→反向投影→变形网格→根据 "变形最大的节点集群" 确定 "接触区域"（颜色越亮 = 接触概率越高）。

3. 关键结果（对应图 8）

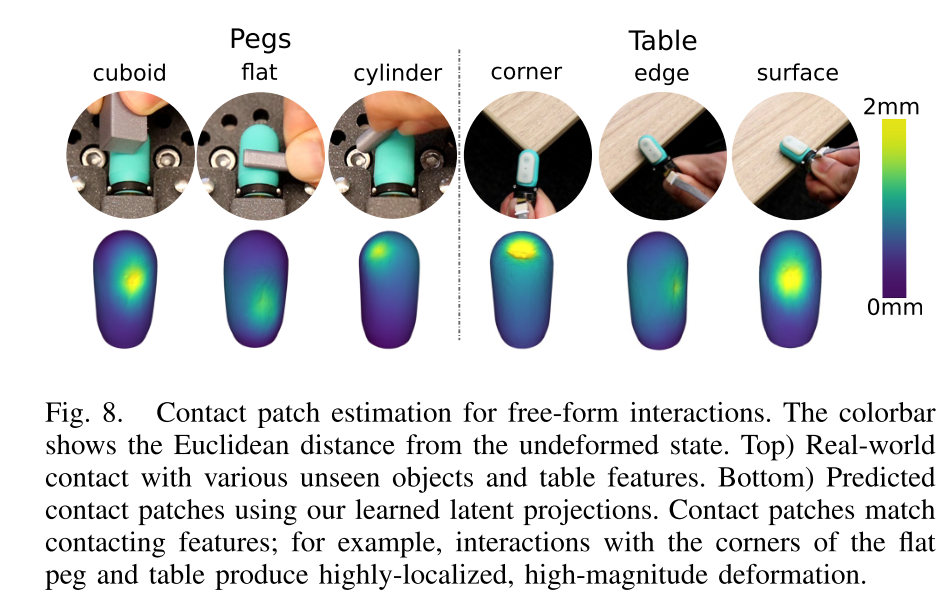
图 8 上半部分是 "真实接触场景"，下半部分是 "预测的接触区域"：

接触位置精准：比如 "桌面角落接触"，预测的接触区域是 "小而亮的斑点"，与真实角落接触位置完全对应；"平面接触" 预测的是 "大范围亮区"，符合平面接触的特点；
细节匹配："立方体 peg 的棱角接触"，预测的接触区域是 "棱角形状的亮区"；"圆柱 peg 接触" 是 "长条状亮区"------ 均与物体的几何特征匹配，证明接触区域估计 "可用、准确"。

这部分通过 "物理验证→学习验证→应用验证" 的三层实验，形成完整证据链：

物理层：FEM 模型 "又快又准"，为 Sim-to-Real 提供高质量数据；
学习层："自监督 + 潜在投影" 能实现双向精准映射，对 "没见过的场景" 泛化性强；
应用层：接触区域估计能直接支撑机器人真实操作，证明研究的实用价值。

最终证明：本文的方法彻底解决了触觉传感 Sim-to-Real 的核心难题 ------"仿真数据可用、现实映射精准、泛化能力强"。