图
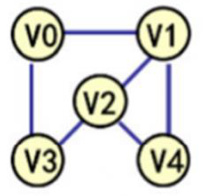
(1) 无向图: 每条边都是无方向的;
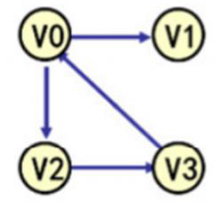
(2) 有向图: 每条边都是有方向的;
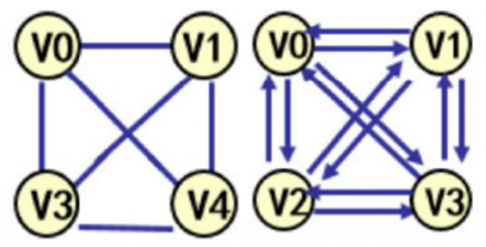
(3) 完全图: 任意两个顶点上都存在一个边;
(4) 子图: 从图中取出的部分集合;
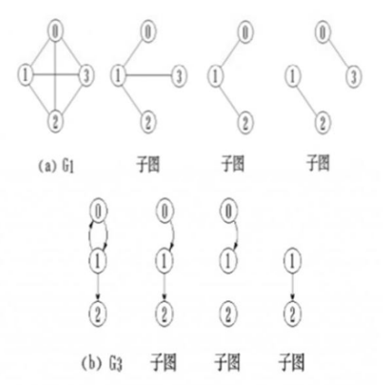
练习
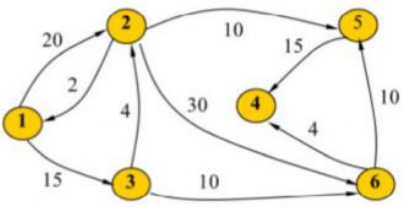
(5) 带权图：边上带权的图；(权：具有某种含义的数值，如表示两点之间的距离)
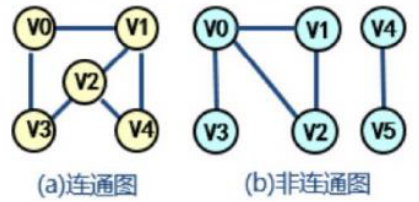
(6) 连通图：无向图中任意两个点都存在路径可达；
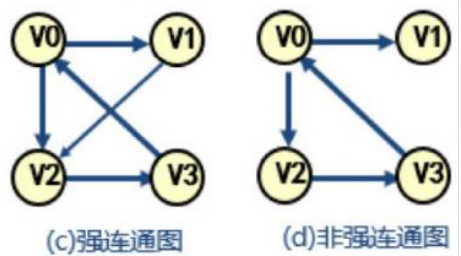
(7) 强连通图：有向图中，若任意两个顶点都存在路径可达；
(8) 顶点的度：与顶点有关的边的数目；
有向图有分为出度和入度；
顶点 V 的出度=以 V 为起点有向边数；
顶点 V 的入度=以 V 为终点有向边数；
顶点 V 的度=V 的出度+V 的入度；
图的度=图中所有顶点度的和；
问题：一个图的顶点数为 n，边数为 e，则该图的度 = 2*e 。
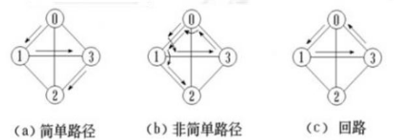
(9) 路径与回路
路径：顶点 A 到顶点 B 的经过的所有的边；
简单路径：在一条路径中，除起点和终点外，若其余顶点各不相同；
回路：起点和终点相同的路径；
简单回路：由简单路径组成的回路称为简单回路；
图的存储
1. 邻接矩阵（数组）表示法
邻接数组表示法是以一个n*n的数组来表示一个具有n个顶点的图形。我们以数组的索引（下标）值来表示顶点，以数组的内容之来表示顶点间边是否存在（1表示存在，0表示不存在）。
例1：无向图的邻接矩阵
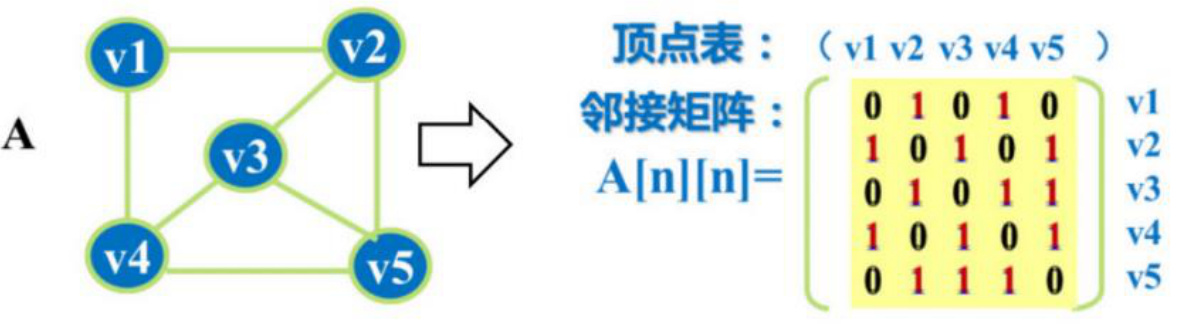根据上述无向图得到邻接矩阵，可以得出如下结论：
- 结论 1: 无向图的邻接矩阵是对称的；
- 结论 2: 顶点 i 的度=第 i 行（列）中 1 的个数；
注意：完全图的邻接矩阵中，对角元素为 0，其余全 1。
例2：有向图的邻接矩阵
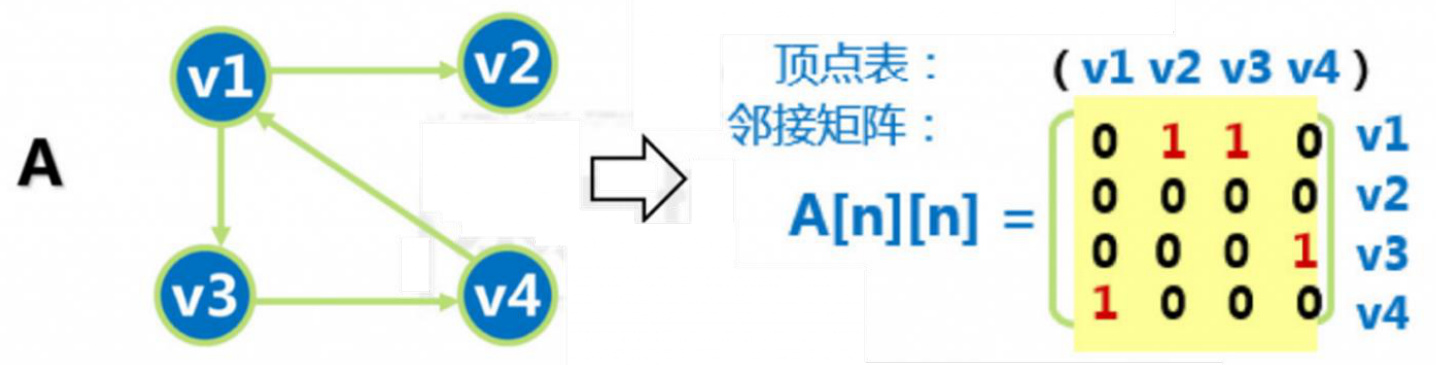
根据上述有向图得到邻接矩阵，可以得出如下结论：
- 结论 1: 有向图的邻接矩阵可能是不对称的；
- 结论 2: 顶点的出度 = 第 i 行元素之和；
顶点的入度 = 第 i 列元素之和；
图的度 = 矩阵中 1 的个数 * 2； - 结论 3: 图的存储空间占用量只与它的顶点数有关，与边数无关；适用于边稠密的图；图的存储
例3：带权图的邻接矩阵
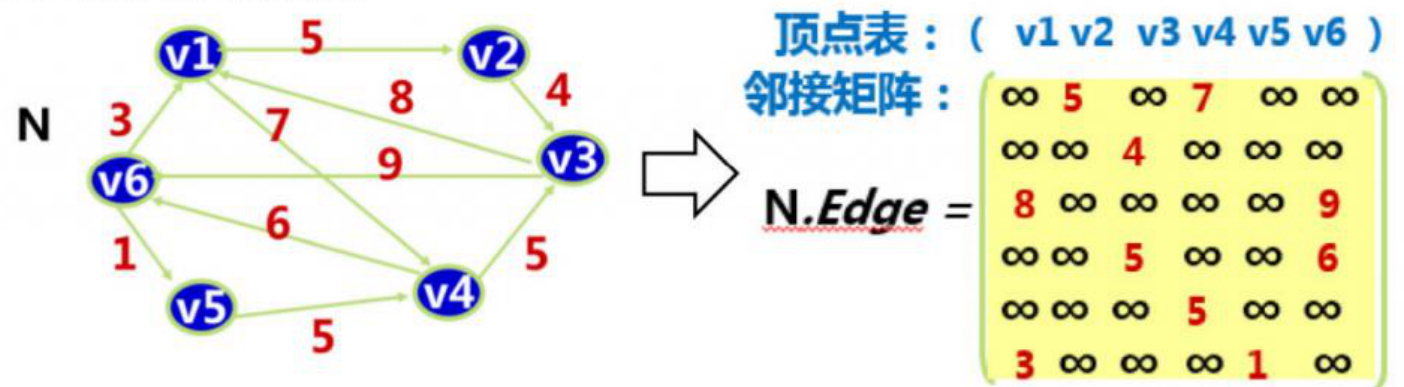
- 邻接矩阵法优点：容易实现图的操作，如：求某顶点的度、判断顶点之间是否有边（弧）、找顶点的邻接点等等。
- 邻接矩阵法缺点：n 个顶点需要 n*n 个单元存储边（弧）。对稀疏图而言尤其浪费空间。
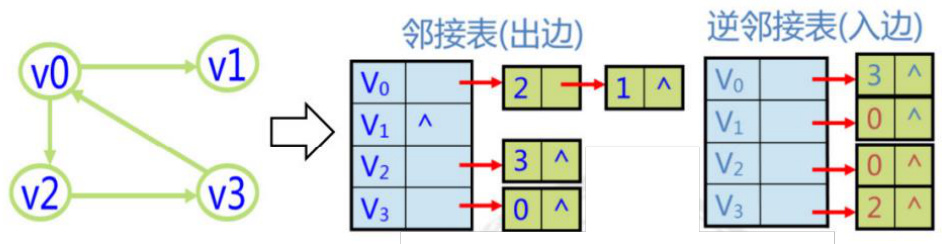
2、邻接（链式）表表示法
邻接链表法：以链表来记录个顶点的邻接顶点。
例 1：无向图的邻接表
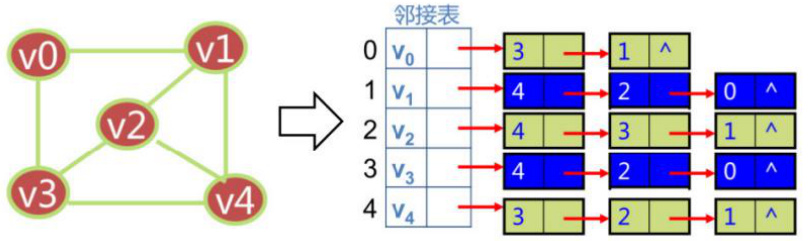
例 2：有向图的邻接表
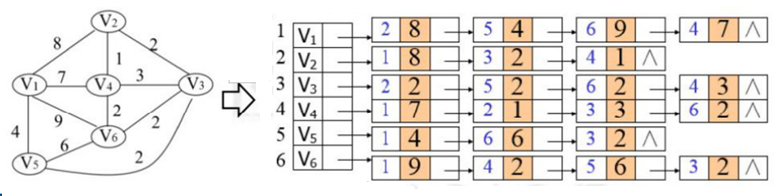
例 3：网（带权图）的邻接链表表示
深度优先遍历与广度优先遍历
深度优先遍历与深搜 dfs 相似，从一个点 A 出发，将这个点标为已访问 visited[i]=true，然后再访问所有与之相连，且未被访问过的点。当 A 的所有邻接点都被访问过后，再退回到 A 的上一个点（假设是 B），再从 B 的另一个未被访问的邻接点出发，继续遍历。
例如对下边的这个无向图深度优先遍历，假定先从 1 出发。程序以如下顺序遍历：
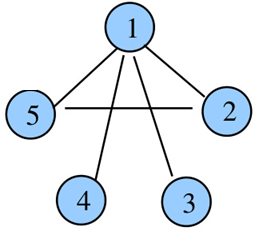
a. 1→2→5，然后退回到 2，退回到 1。
b. 从 1 开始再访问未被访问过的点 3，3 没有未访问的邻接点，退回
c. 再从 1 开始访问未被访问过的点 4，再退回 1。
d. 起点 1 的所有邻接点都已访问，遍历结束。
广度优先遍历并不常用，从编程复杂度的角度考虑，通常采用的是深度优先遍历。
广度优先遍历和广搜 bfs 相似，因此使用广度优先遍历一张图并不需要掌握什么新的知识，在原有的广度优先搜索的基础上，做一点小小的修改，就成了广度优先遍历算法。
一笔画问题
如果一个图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。
定义奇点是指跟这个点相连的边数目有奇数个的点。对于能够一笔画的图，于是有以下两个定理。
- 定理 1：存在欧拉路的条件：图是连通的，有且只有 2 个奇点。
- 定理 2：存在欧拉回路的条件：图是连通的，有 0 个奇点。
两个定理的正确性是显而易见的，既然每条边都要经过一次，那么对于欧拉路，除了起点和终点外，每个点如果进入了一次，显然一定要出去一次，显然是偶点。对于欧拉回路，每个点进入和出去次数一定都是相等的，显然没有奇点。
求欧拉路的算法很简单，使用深度优先遍历即可。
根据一笔画的两个定理，如果寻找欧拉回路，对任意一个点执行深度优先遍历；找欧拉路，则对一个奇点执行 dfs，时间复杂度为 O(m+n)，m 为边数，n 是点数。