基于物理信息神经网络(PINN)求解二维热传导方程的完整MATLAB实现。以下是对代码的全面分析:
一、主要功能
- 热传导方程求解:模拟带有空腔的二维材料块在不同初始和边界条件下的瞬态热传导过程
- PINN训练:训练神经网络学习从初始/边界条件到温度场的映射关系
- 物理约束嵌入:将热传导方程作为正则项加入损失函数,确保网络预测符合物理规律
- 多条件学习:同时学习多种初始和边界条件下的热传导行为
二、算法步骤
数据准备阶段:
- 从Excel文件读取初始条件和边界条件
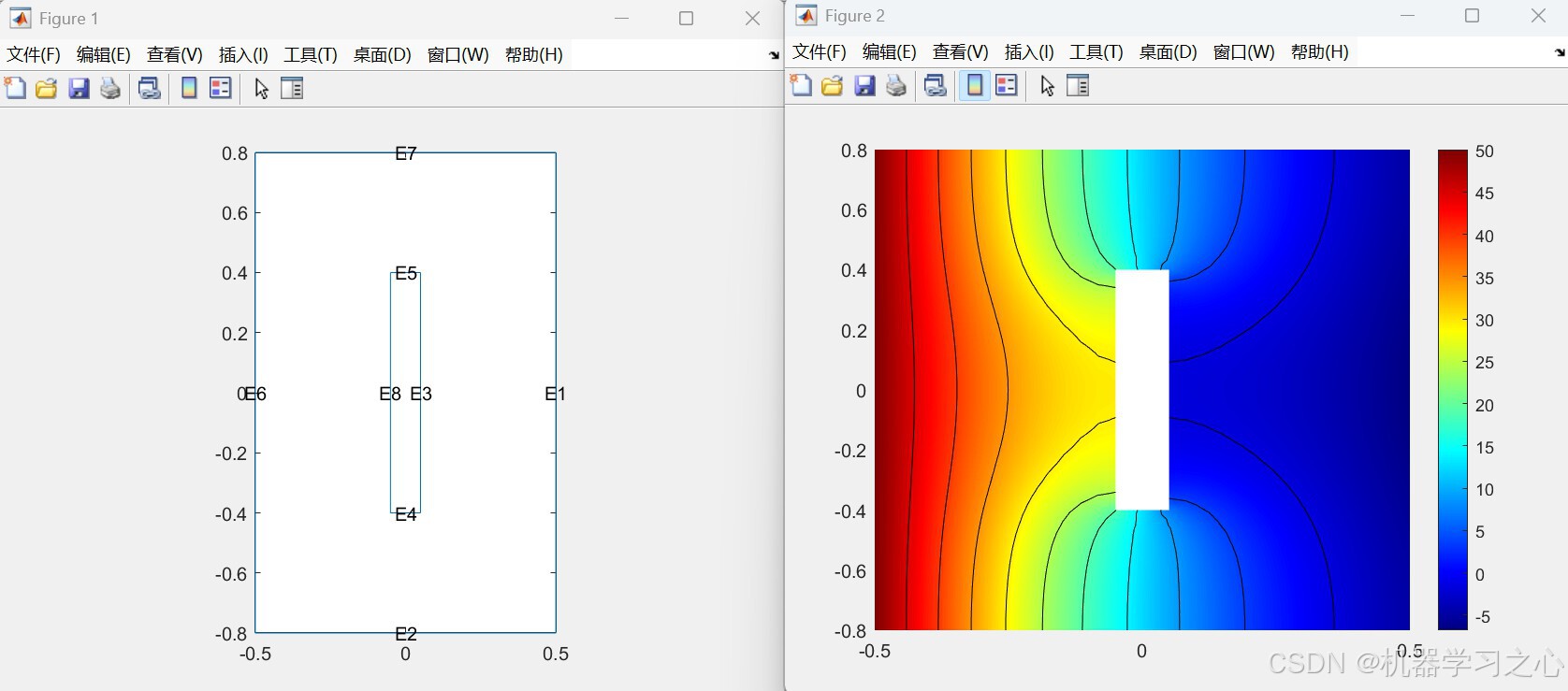
- 使用PDE工具箱创建热模型并设置几何形状(带空腔的矩形)
- 并行求解不同条件下的热传导方程生成训练数据
- 提取温度场及其空间梯度作为训练目标
网络训练阶段:
- 构建多层感知机神经网络
- 定义包含数据损失和物理损失的复合损失函数
- 使用Adam优化器进行训练
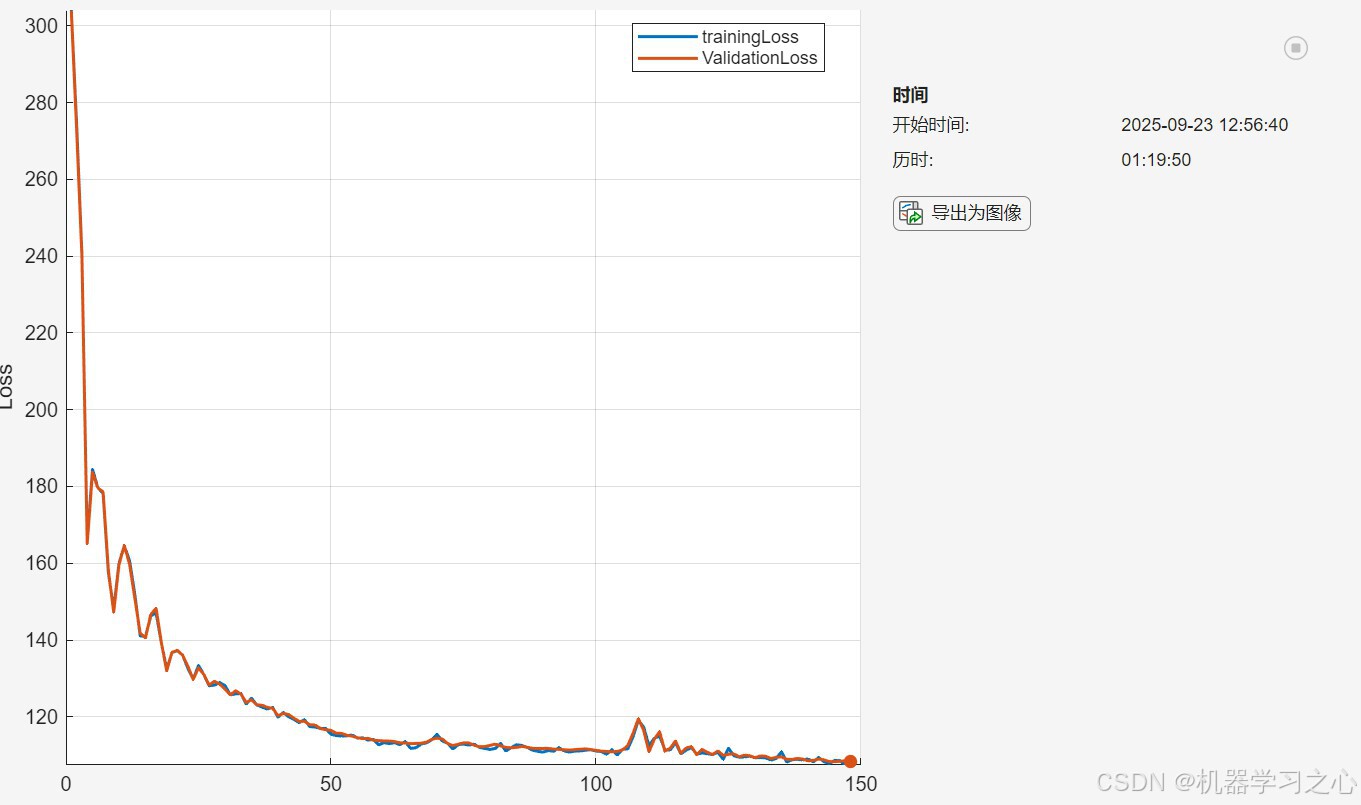
- 实时监控训练和验证损失
预测验证阶段:
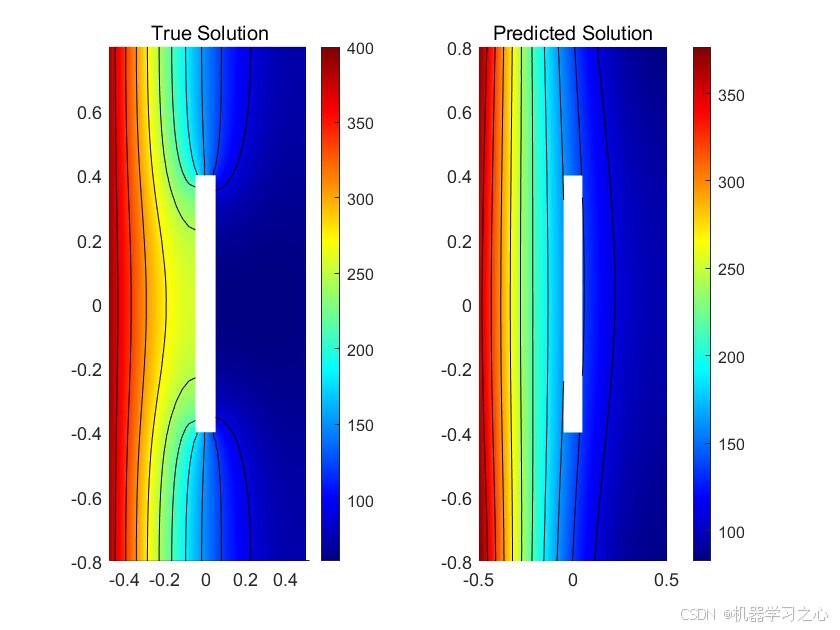
- 在未见过的边界条件下测试网络性能
- 对比PINN预测与PDE工具箱求解的真实解
- 可视化预测结果
三、技术路线
| 技术组件 | 实现方式 |
|---|---|
| 神经网络架构 | 多层感知机(MLP) + tanh激活函数 |
| 物理约束 | 热传导方程残差作为PINN损失项 |
| 自动微分 | dlgradient计算空间和时间导数 |
| 优化算法 | Adam优化器 + 固定学习率 |
| 数据加速 | dlaccelerate加速损失函数计算 |
| 并行计算 | parfor并行求解PDE生成数据 |
四、公式原理
热传导方程(控制方程):
∂ u ∂ t = α ∇ 2 u \frac{\partial u}{\partial t} = \alpha \nabla^2 u ∂t∂u=α∇2u
其中:
- u(t,x,y) :温度场
- \\alpha :热扩散系数(本例中设为1)
- ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 \nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} ∇2=∂x2∂2+∂y2∂2:拉普拉斯算子
PINN损失函数:
L = L data + L PINN \mathcal{L} = \mathcal{L}{\text{data}} + \mathcal{L}{\text{PINN}} L=Ldata+LPINN
L data = ∥ u pred − u true ∥ + ∥ ∇ u pred − ∇ u true ∥ \mathcal{L}{\text{data}} = \|u{\text{pred}} - u_{\text{true}}\| + \|\nabla u_{\text{pred}} - \nabla u_{\text{true}}\| Ldata=∥upred−utrue∥+∥∇upred−∇utrue∥
L PINN = ∥ ∂ u ∂ t − ∇ 2 u ∥ \mathcal{L}_{\text{PINN}} = \left\| \frac{\partial u}{\partial t} - \nabla^2 u \right\| LPINN= ∂t∂u−∇2u
五、参数设定
物理参数:
- 热导率:1
- 密度:1
- 比热:1
- 求解时间:0-0.1s,步长0.01s
网络参数:
- 隐藏层大小:10神经元
- 隐藏层数:2层
- 激活函数:tanh
- 输出层:sigmoid(限制输出范围)
训练参数:
- 最大训练轮数:300
- 学习率:0.1
- 批量大小:1308×50
- 优化器:Adam
输入特征(6维):
- 时间 ( t )
- 空间坐标 ( x )
- 空间坐标 ( y )
- 初始条件 ( u_0 )
- Dirichlet边界条件(边缘6温度)
- Neumann边界条件(边缘1热通量)
六、运行环境
软件要求:
- MATLAB(R2024b或更高版本)
数据文件:
Condition.xlsx:初始和边界条件data.mat:PDE求解结果缓存
七、应用场景
工程领域:
- 电子设备散热分析:预测芯片在不同功率下的温度分布
- 材料加工:模拟热处理过程中的温度场演化
- 建筑热工:分析墙体结构的传热性能
科学研究:
- 逆向问题:从温度测量反推材料热物性参数
- 参数化研究:快速评估不同边界条件对温度场的影响
- 实时仿真:训练后的网络可实现近乎实时的温度预测
方法学价值:
- 数据物理融合:示范如何将物理定律与数据驱动方法结合
- 算子学习:展示神经网络学习偏微分方程解算子的能力
- 多物理场建模:为其他物理场的PINN应用提供模板
总结
该代码实现了一个完整的PINN框架用于热传导问题,其核心价值在于:
- 物理一致性:通过嵌入热方程确保预测符合物理规律
- 泛化能力:可处理训练数据未覆盖的边界条件
- 计算效率:训练后前向预测远快于数值求解PDE
- 模块化设计:清晰分离数据生成、网络训练和验证测试