分解+降维+物理信息神经网络!EEMD-KPCA-PINN多变量时序光伏功率预测,MATLAB代码。以下是对代码的全面分析:
一、主要功能
该代码用于光伏功率时间序列预测,结合了信号分解、特征降维和物理约束神经网络,实现对光伏发电功率的高精度预测。
二、算法步骤
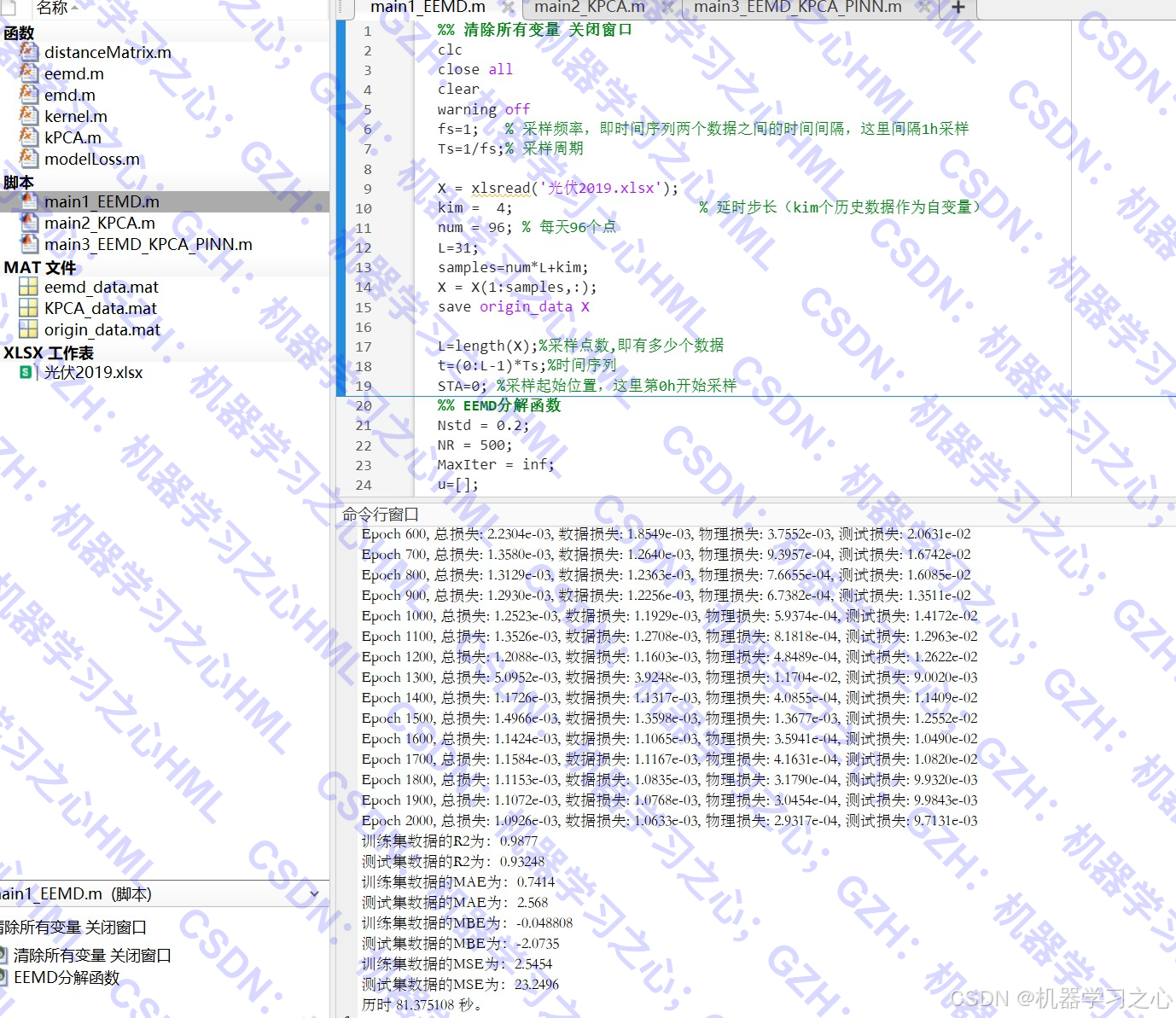
1. 数据预处理(main1_EEMD.m)
- 读取光伏功率数据(每小时一个点,每天96个点)
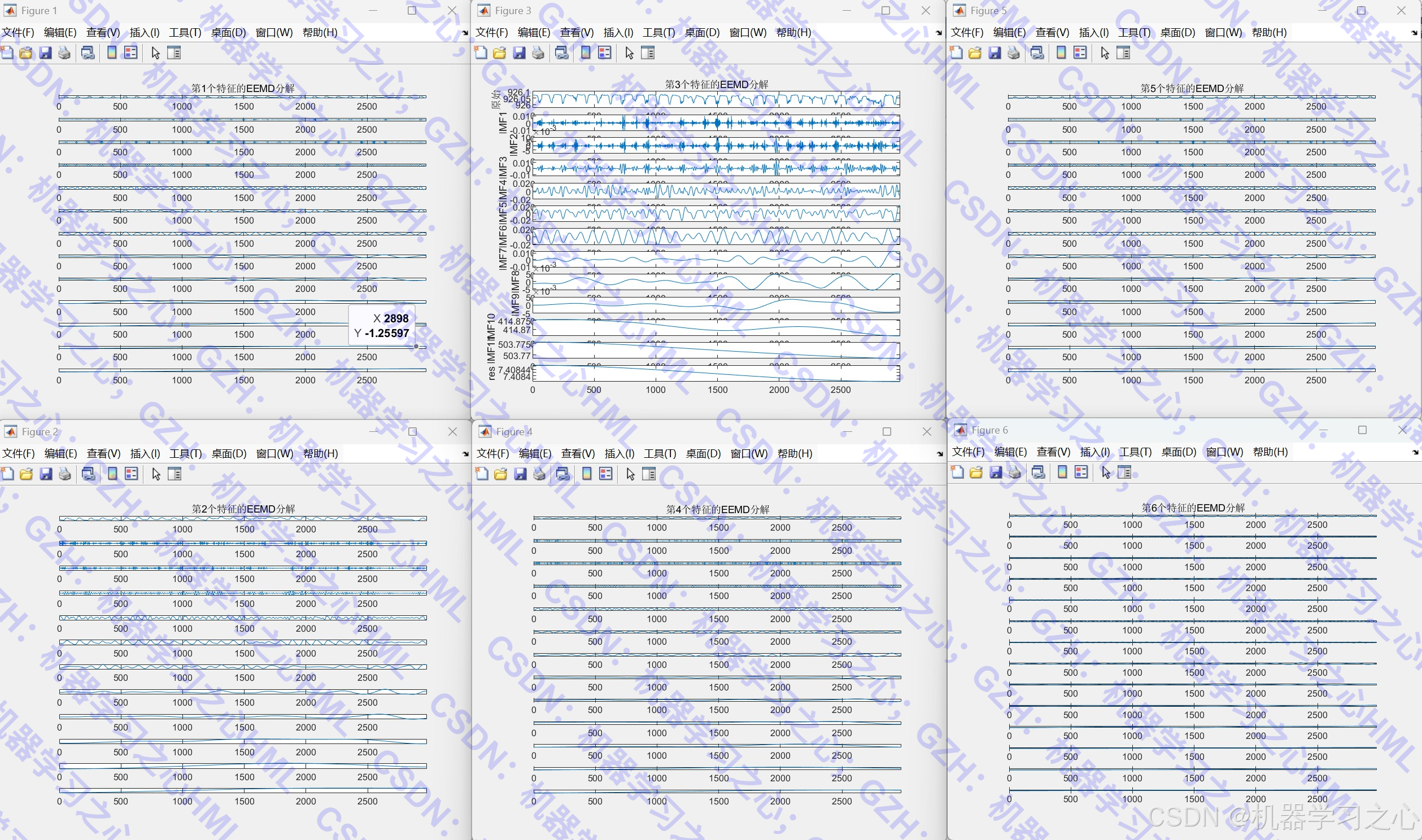
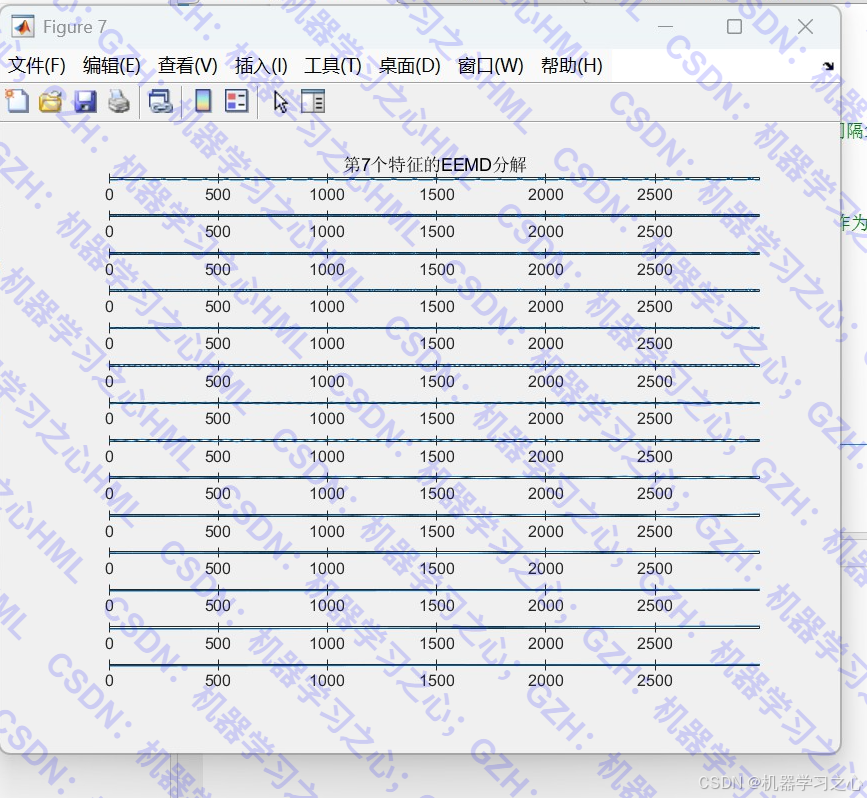
- 使用 EEMD(集合经验模态分解) 对每个特征进行分解
- 将原始信号分解为多个IMF(本征模态函数)和残差项
- 可视化分解结果并保存
2. 特征降维(main2_KPCA.m)
- 加载EEMD分解后的数据
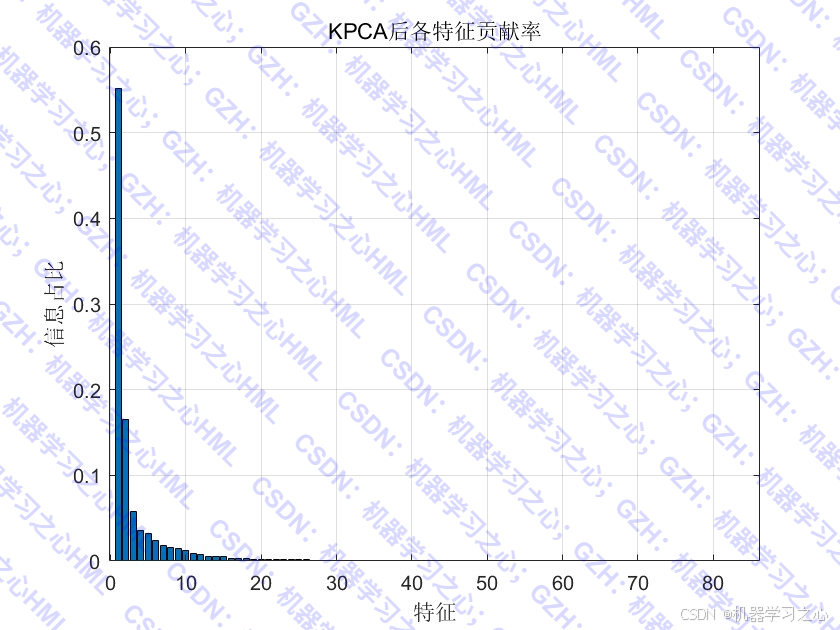
- 使用 KPCA(核主成分分析) 进行特征降维
- 计算累积贡献率,保留贡献率>90%的主成分
- 保存降维后的数据
3. PINN预测建模(main3_EEMD_KPCA_PINN.m)
- 重构数据集(时间序列滑窗处理)
- 划分训练集(30天)和测试集(第31天)
- 数据归一化
- 构建物理信息神经网络(PINN) 模型
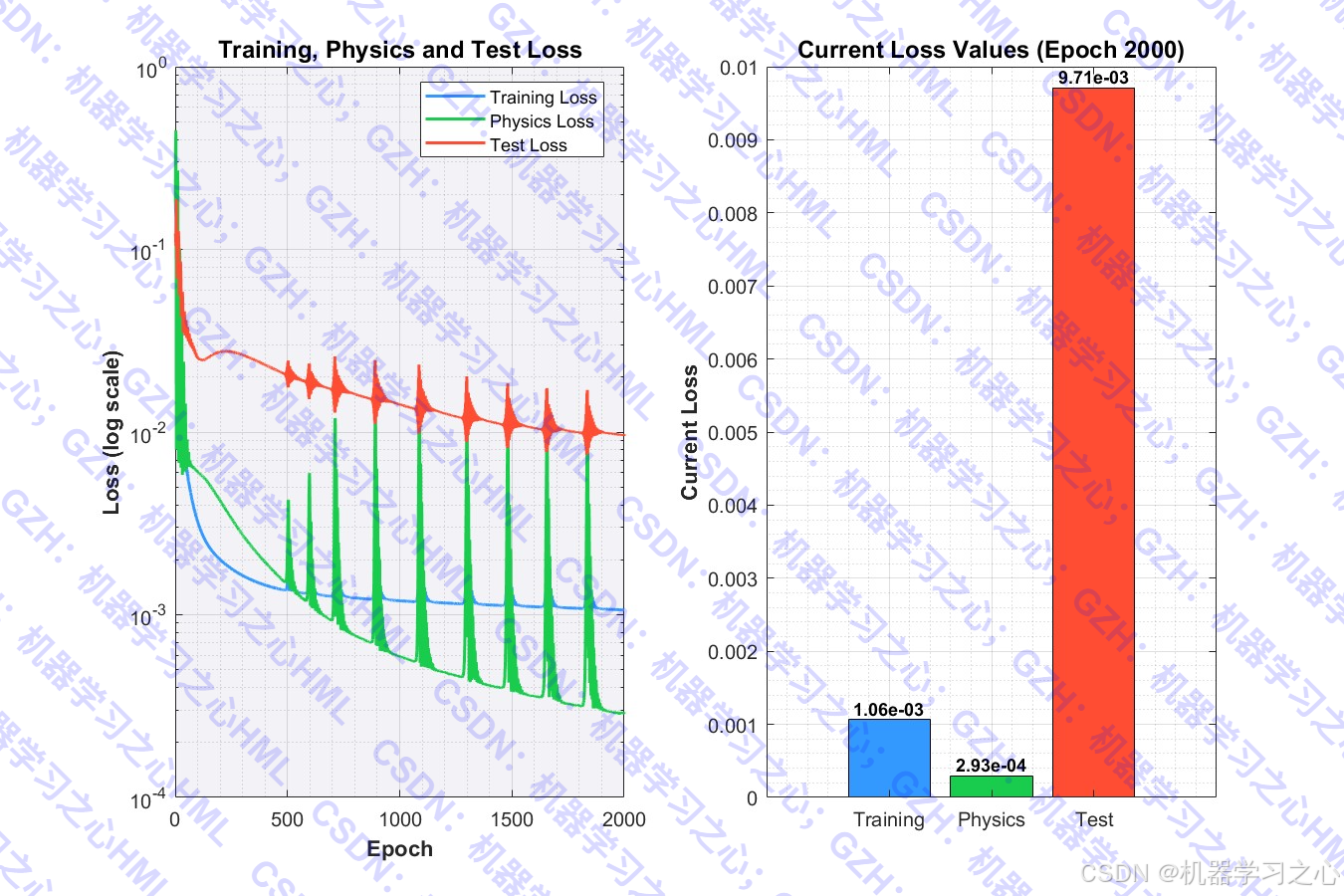
- 训练模型(含物理约束损失)
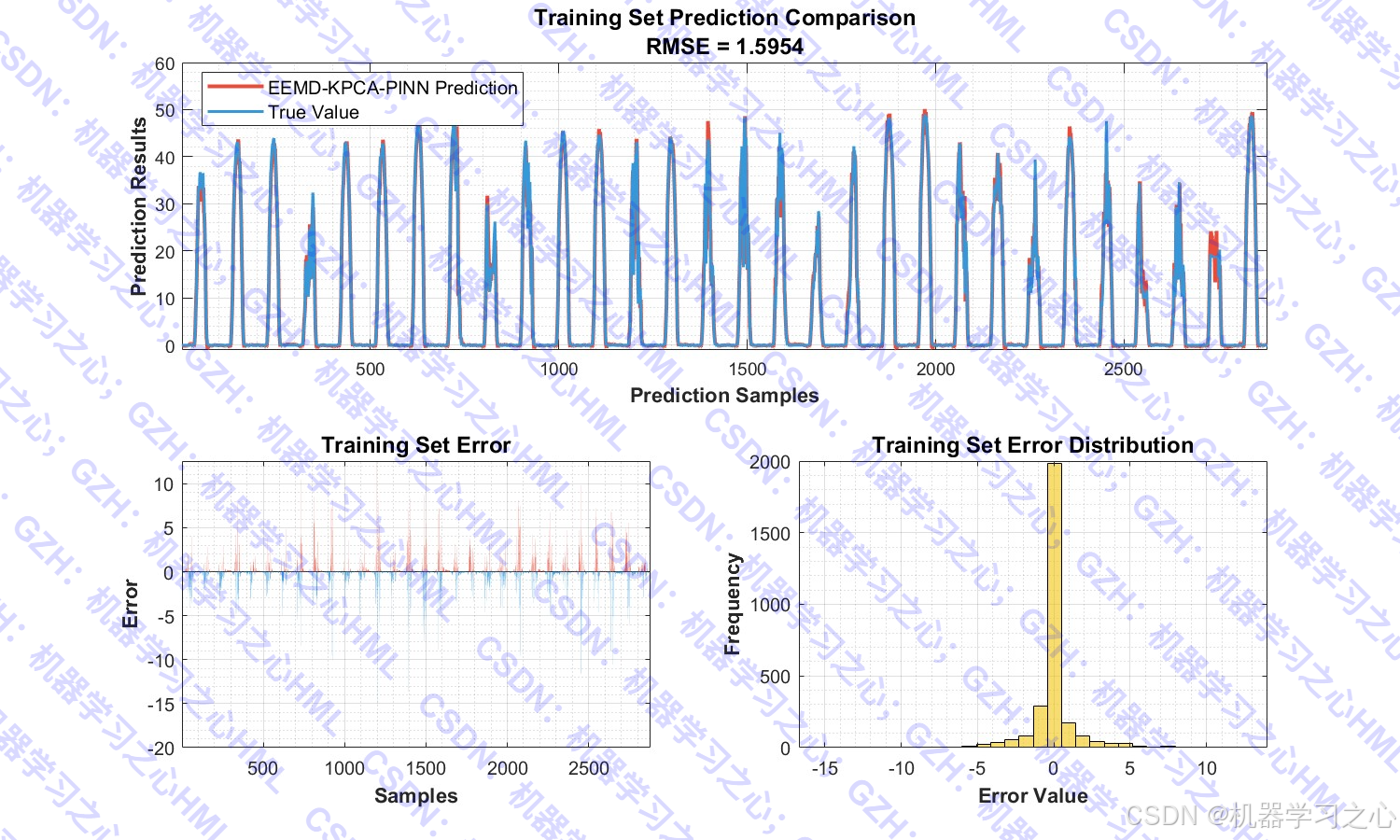
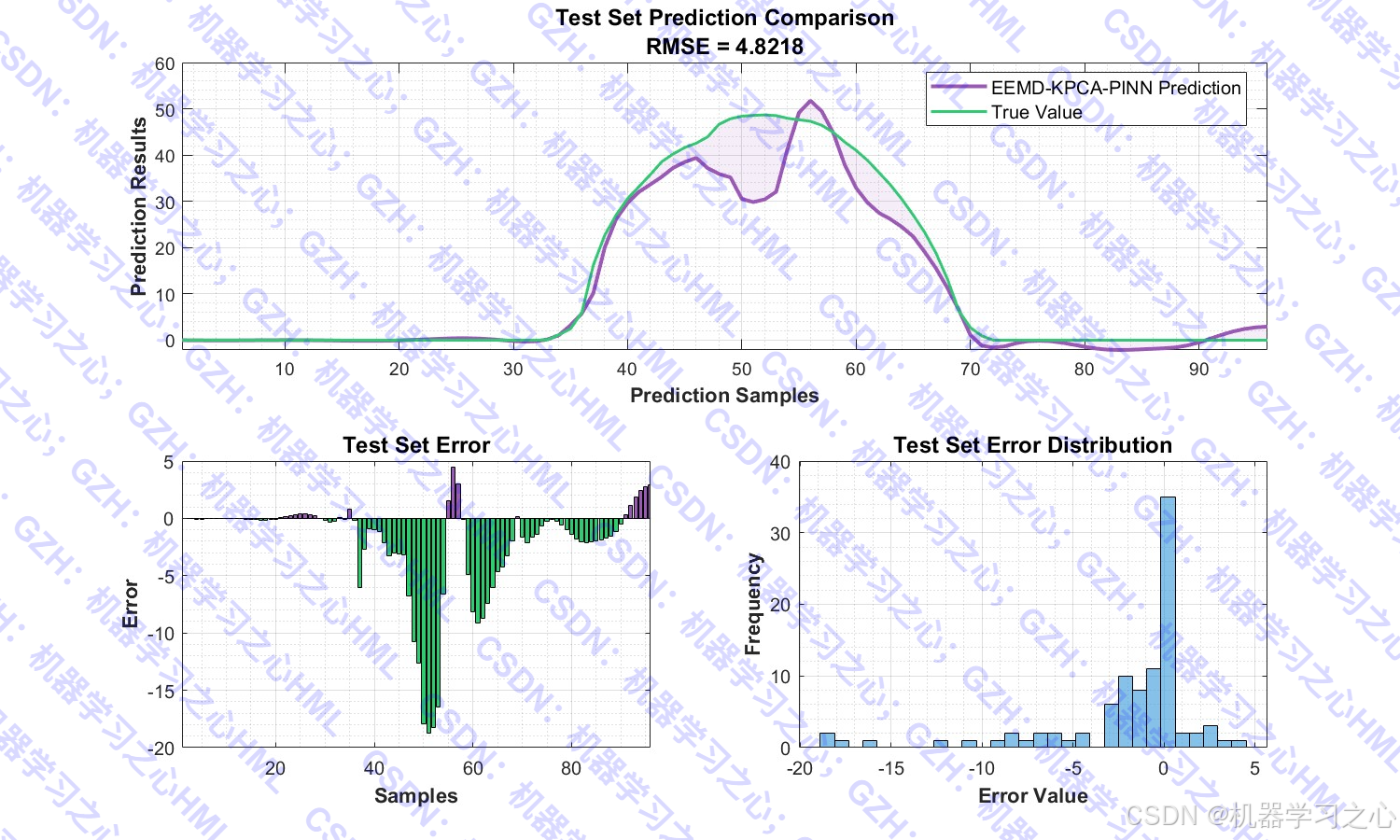
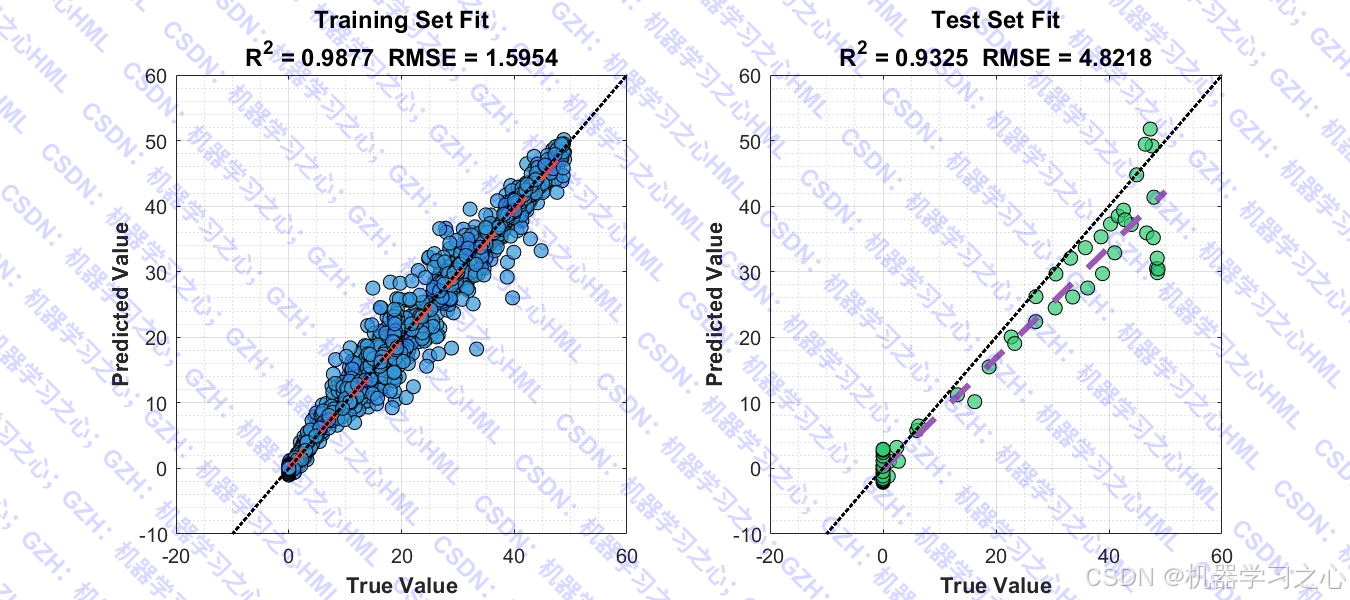
- 预测并评估模型性能
三、技术路线
原始光伏数据
↓
EEMD信号分解 → 多尺度特征提取
↓
KPCA特征降维 → 保留主要信息,去除冗余
↓
构建时序样本(滑窗法)
↓
划分训练集/测试集
↓
PINN建模(含物理约束)
↓
预测与评估四、公式原理
1. EEMD分解
在EMD基础上加入高斯白噪声,通过多次分解求平均来抑制模态混叠:
xi(t)=x(t)+ε⋅ni(t) x_i(t) = x(t) + ε·n_i(t) xi(t)=x(t)+ε⋅ni(t)
IMF=average(EMD(xi(t))) IMF = average(EMD(x_i(t))) IMF=average(EMD(xi(t)))
2. KPCA降维
通过核函数将数据映射到高维特征空间,再进行PCA:
K(xi,xj)=(xi⋅xj+c)d K(x_i, x_j) = (x_i·x_j + c)^d K(xi,xj)=(xi⋅xj+c)d
特征值分解:Kα=λα 特征值分解:Kα = λα 特征值分解:Kα=λα
3. PINN损失函数
总损失=数据损失+λ⋅物理损失 总损失 = 数据损失 + λ·物理损失 总损失=数据损失+λ⋅物理损失
数据损失=MSE(ypred,ytrue) 数据损失 = MSE(y_pred, y_true) 数据损失=MSE(ypred,ytrue)
物理损失=PDE约束 物理损失 = PDE约束 物理损失=PDE约束
五、参数设定
数据参数:
- 采样频率:
fs = 1(每小时) - 每天样本数:
num = 96 - 训练天数:
L1 = 30 - 预测天数:
L2 = 31 - 延时步长:
kim = 4
EEMD参数:
- 噪声标准差:
Nstd = 0.2 - 集合次数:
NR = 500 - 最大迭代次数:
MaxIter = inf
KPCA参数:
- 核函数:多项式核
'poly' - 核参数:
para = 10
PINN参数:
- 网络结构:
64-64-64-1(3个隐藏层) - 激活函数:tanh
- 训练轮数:
numEpochs = 2000 - 学习率:
learningRate = 0.001 - 物理损失权重:
lambda_phys = 0.1
六、运行环境
- 平台:MATLAB R2024b
- 必要工具箱 :
- Signal Processing Toolbox
- Deep Learning Toolbox
- Statistics and Machine Learning Toolbox
七、应用场景
- 光伏电站功率预测:用于电力系统调度
- 电力市场交易:提供日前功率预测报价
- 可再生能源研究:评估光伏发电特性
八、模型特点
- ✅ 多尺度分析:EEMD提取不同频率特征
- ✅ 维度压缩:KPCA去除冗余信息
- ✅ 物理约束:PINN引入光伏功率变化规律
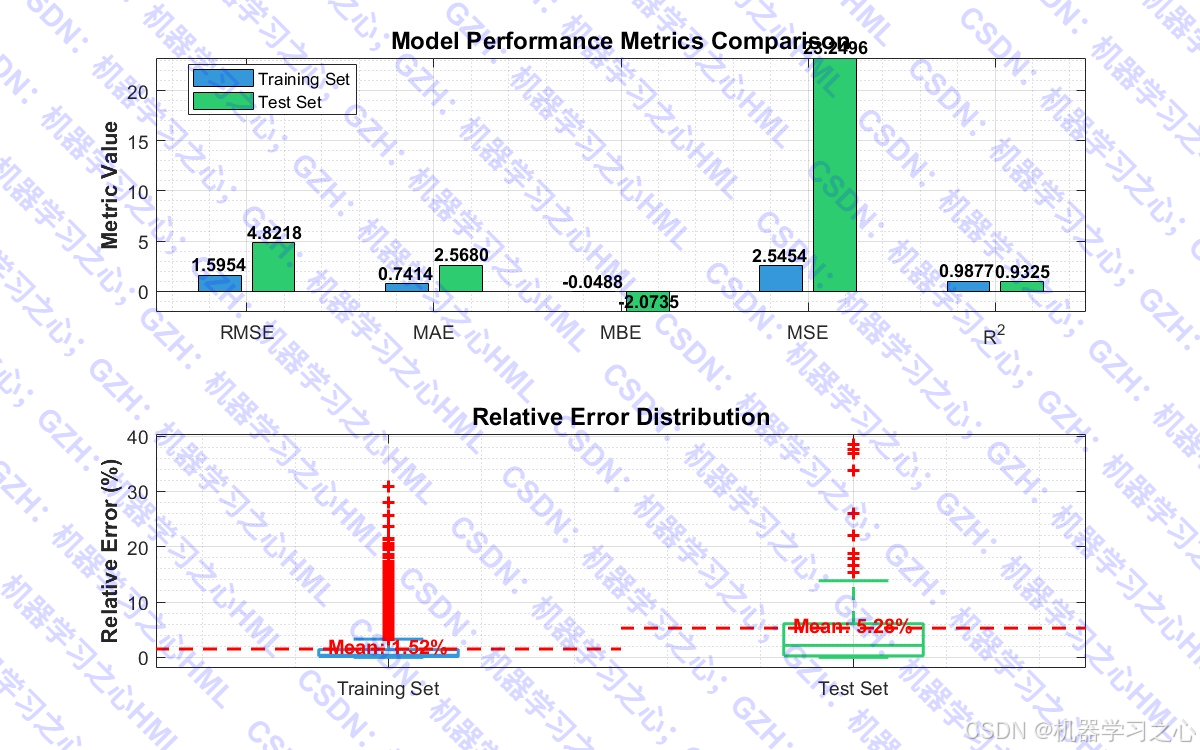
- ✅ 可视化丰富:极坐标图、误差分布、性能汇总
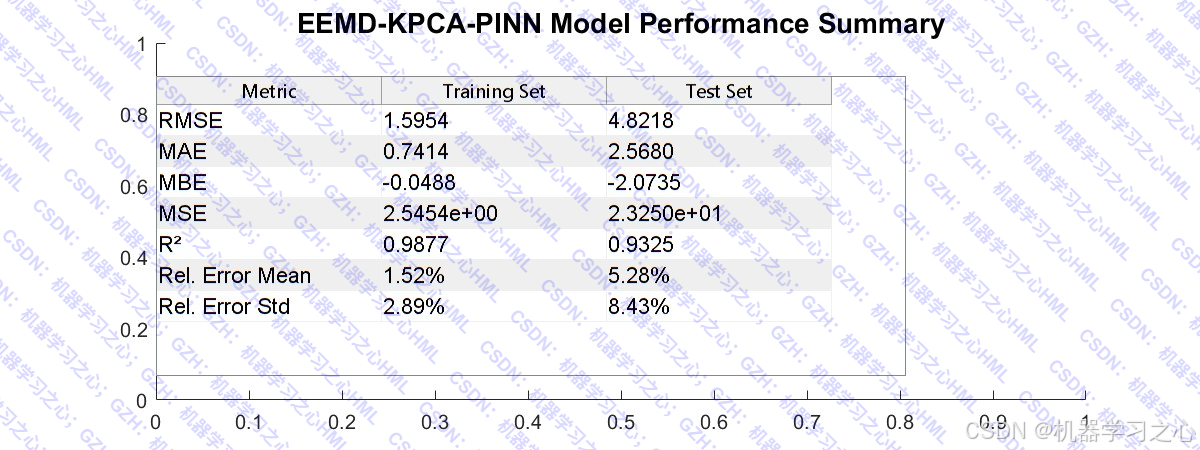
- ✅ 评估全面:RMSE、MAE、MBE、MSE、R² 多指标