目录
1.两数之和
python
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值target的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
输入:nums = [3,2,4], target = 6
输出:[1,2]实现代码
python
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
for i in range(len(nums)):
res=target-nums[i]
if res in nums[i+1:]:
#转换为原列表的索引
return [i,nums[i+1:].index(res)+i+1]
python
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
dict={}
for index,value in enumerate(nums):
res=target-value
if res in dict:
return [dict[res],index]
dict[value]=index
return [] 基础知识
(1)遍历索引:如果需要获取列表中元素的位置(索引),用range(len(列表)):
(2)同时获取索引和元素:用enumerate()函数,一次拿到索引和对应的值
(3)在 Python 中,index() 是列表(list)的一个内置方法,用于查找某个元素在列表中第一次出现的位置(索引)
(4) 类:可以理解为一个「模板」,定义了某类事物的共同特征和行为(比如「人」这个类,有姓名、年龄等特征,有走路、说话等行为)。
对象:是类的具体「实例」(比如「张三」就是「人」这个类的一个对象)。
self 的核心作用是指代当前对象本身,让类中的方法知道自己正在操作哪个对象的数据。
self 就像一个「代词」,在类的方法中代表「当前正在操作的对象」。有了它,类才能区分不同对象的数据,让每个对象能独立地使用类中定义的方法。
2.字母异位词分组
python
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
解释:
在 strs 中没有字符串可以通过重新排列来形成 "bat"。
字符串 "nat" 和 "tan" 是字母异位词,因为它们可以重新排列以形成彼此。
字符串 "ate" ,"eat" 和 "tea" 是字母异位词,因为它们可以重新排列以形成彼此。
示例 2:
输入: strs = [""]
输出: [[""]]实现代码
用哈希表分组,把排序后的字符串当作哈希表的 key,排序前的字符串加到对应的列表中(哈希表的 value)。最后把哈希表的所有 value 加到一个列表中返回。
python
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
d=defaultdict(list)
for s in strs:
sorts=''.join(sorted(s))
d[sorts].append(s)
return list(d.values())基础知识
(1)列表
python
# 1. 创建列表
list1 = [] # 空列表
list2 = [1, 2, 3, "hello", True] # 元素可以是不同类型
# 2. 访问元素(通过索引,索引从0开始)
print(list2[0]) # 输出:1(第一个元素)
print(list2[-1]) # 输出:True(最后一个元素,-1表示倒数第一)
# 3. 修改元素
list2[0] = 100
print(list2) # 输出:[100, 2, 3, "hello", True]
# 4. 切片(获取子列表,语法:list[start:end:step],左闭右开)
print(list2[1:4]) # 输出:[2, 3, "hello"](从索引1到3)
print(list2[::2]) # 输出:[100, 3, True](步长为2,隔一个取一个)
python
list3 = [1, 2, 3]
# 添加元素
list3.append(4) # 末尾添加:[1, 2, 3, 4]
list3.insert(1, 10) # 指定位置插入(索引1处):[1, 10, 2, 3, 4]
# 删除元素
list3.remove(2) # 删除第一个值为2的元素:[1, 10, 3, 4]
list3.pop(0) # pop()函数用于从列表中移除一个元素,并返回该元素的值。如果没有指定索引,pop()将默认移除列表中的最后一个元素。[10, 3, 4]
# 其他常用
list3.extend([5, 6]) # 合并另一个列表:[10, 3, 4, 5, 6]
print(list3.index(3)) # 查找元素3的索引:1
print(list3.count(10)) # 统计元素10出现的次数:1
list3.sort() # 排序(默认升序):[3, 4, 5, 6, 10]
list3.reverse() # 反转:[10, 6, 5, 4, 3](2)列表推导式:[表达式 for 变量 in 可迭代对象 if 条件]
python
# 生成1-10的偶数列表
even_numbers = [x for x in range(1, 11) if x % 2 == 0]
print(even_numbers) # 输出:[2, 4, 6, 8, 10](3)defaultdict 是 Python collections 模块中的一个类,它是普通字典的子类。与普通字典不同的是:
- 当访问一个不存在的键时,它会自动创建该键,并将默认值(这里是
list(),即空列表)赋值给它 - 普通字典访问不存在的键会抛出
KeyError错误
3.移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序
实现代码
python
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
if not nums:
return
j=0
for i in range(len(nums)):
if nums[i]:
nums[j],nums[i]=nums[i],nums[j]
j=j+1 记录非零的个数,并且移动,最后再添加上零
python
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
if not nums:
return
j=0
for i in range(len(nums)):
if nums[i]:
nums[j]=nums[i]
j=j+1
for i in range(j,len(nums)):
nums[i]=0 4.相交链表
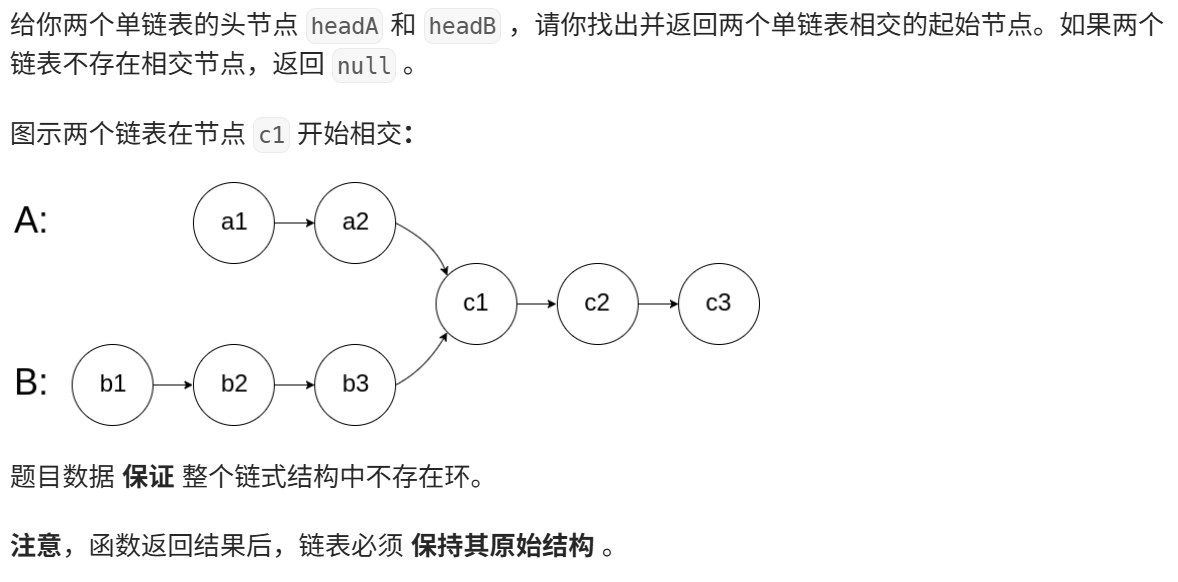
实现代码
(1)暴力
时间复杂度O(n²),空间复杂度O(1)
python
class Solution(object):
def getIntersectionNode(self, headA, headB):
"""
:type head1, head1: ListNode
:rtype: ListNode
"""
p=headA
while p:
q=headB
while q:
if p==q:
return p
q=q.next
p=p.next
return None(2)哈希表
先将其中一个链表存到哈希表中,此时再遍历另外一个链表查找重复结点只需 O(1) 时间
时间复杂度O(n),空间复杂度O(n)
python
class Solution(object):
def getIntersectionNode(self,headA,headB):
s=set()
p,q=headA,headB
while p:
s.add(p)
p=p.next
while q:
if q in s:
return q
q=q.next
return None(3)栈
时间复杂度O(n),空间复杂度O(n)
python
class Solution(object):
#返回第一个不一样的节点
def getIntersectionNode(self,headA,headB):
s1=[]
s2=[]
p,q=headA,headB
while p:
s1.append(p)
p=p.next
while q:
s2.append(q)
q=q.next
#获得栈顶的索引
i,j=len(s1)-1,len(s2)-1
ans=None
while i>=0 and j>=0 and s1[i]==s2[j]:
ans=s1[i]
i=i-1
j=j-1
return ans(4)计算长度
时间复杂度O(n),空间复杂度O(1)
python
class Solution(object):
#计算长度
def getIntersectionNode(self,headA,headB):
s1=0
s2=0
p,q=headA,headB
while p:
s1=s1+1
p=p.next
while q:
s2=s2+1
q=q.next
p,q=headA,headB
for i in range(s1-s2):
p=p.next
for i in range(s2-s1):
q=q.next
while p and q and p!=q:
p=p.next
q=q.next
return q(5)走过彼此的路
时间复杂度O(n),空间复杂度O(1)
前一种方法是计算两链表的长度差,然后让长链表先走掉长度差的部分。该方法则利用两链表长度和相等的性质。让两个指针分别遍历两个链表,当一个指针遍历完自己的链表后,转到另一个链表的头部继续遍历,最终两个指针会在相交节点相遇(如果存在的话)。
python
class Solution(object):
def getIntersectionNode(self,headA,headB):
p,q=headA,headB
while p!=q:
p=p.next if p else headB
q=q.next if q else headA
return p当两链表长度相等时,指针同步走,如果有共同节点,将会找到。
当两链表长度不相等时,假设存在共同节点,A、B链表均分为两部分,一部分共同节点的前面部分,另外一部分为共同节点后面一致的部分,A(a+c),B(b+c),则交叉遍历A走过的路径是a+c+b,B走过的路径是b+c+a。所以能找到共同节点,如果不存在共同节点,则两链表都会走到对方链表的尾端,返回None.
基础知识
(1)链表ListNode节点的定义:链表节点通常定义为一个类,用于存储数据和指向下一个节点的引用。
python
class ListNode:
def _init_(self,x):
self.val=x # 节点存储的数据(值)
self.next=None # 指向下一个节点的引用(默认为None,表示没有下一个节点)(2)while后面跟条件表达式 ,当表达式为True时循环继续,为False时循环结束。如果p是一个有效对象(非None),则被视为True。
5.反转链表
实现代码
(1)申请外部空间
python
class Solution(object):
def reverseList(self, head):
s=[]
p=head
while p:
s.append(p.val)
p=p.next
s.reverse()
p=head
for val in s:
p.val=val
p=p.next
return head(2)双指针迭代
申请两个指针,pre指向None,cur指向head,不断遍历cur,每次迭代到cur,都利用tmp保存cur的next的位置(方便后面cur的前进),然后cur指向pre(反转链表的指向),pre和cur同时前进一步
python
class Solution(object):
def reverseList(self, head):
pre=None
cur=head
while cur:
tmp=cur.next
cur.next=pre
pre=cur
cur=tmp
return pre(3)递归
python
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
return self.reverse(head,None)
def reverse(self,cur,pre):
if cur==None:return pre
tmp=cur.next
cur.next=pre
return self.reverse(tmp,cur)6.回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
实现代码
(1)双指针法
时间复杂度O(n),空间复杂度O(n)
列表实现分为数组列表和链表,如果我们想要在列表中存储值,我们是如何实现的呢?数组列表底层是利用数组存储值,我们可以通过索引再O(1)时间访问列表任何位置的值,这是基于内存寻址的方式。链表存储的是节点的对象,每个节点保存的是节点的值和指向下一个节点的指针,访问某个特定索引的节点需要O(n)的时间,因为需要通过指针获取下一个位置的节点。
确定数组列表是否回文很简单,我们可以使用双指针法来比较两端的元素,并向中间移动。一个指针从起点向中间移动,另一个指针从终点向中间移动。这需要 O(n) 的时间,因为访问每个元素的时间是 O(1),而有 n 个元素要访问。
python
class Solution(object):
def isPalindrome(self, head):
"""
:type head: Optional[ListNode]
:rtype: bool
"""
s=[]
p=head
while p:
s.append(p.val)
p=p.next
return s==s[::-1]7.有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的 字母异位词。
实现代码
python
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
record=[0]*26
for i in s:
record[ord(i)-ord('a')]+=1
for i in t:
record[ord(i)-ord('a')]-=1
for i in range(26):
if record[i]!=0:
return False
return True8.合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
实现方法
python
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
dummy_head=ListNode(0)
cur=dummy_head
while list1 and list2:
if list1.val>=list2.val:
cur.next=list2
list2=list2.next
cur=cur.next
else:
cur.next=list1
list1=list1.next
#记得移动cur
cur=cur.next
cur.next=list1 if list1 else list2
return dummy_head.next9.有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
实现方法
python
class Solution(object):
def isValid(self, s):
"""
:type s: str
:rtype: bool
"""
dict={")":"(","]":"[","}":"{"}
stack=[]
#遍历字符串,左括号进栈,右括号出栈
for i in s:
if stack and i in dict:
if stack[-1]==dict[i]:
stack.pop()
else:
return False
else:
stack.append(i)
#如果最后栈为空,则属于有效括号
return not stack
python
class Solution:
def isValid(self, s: str) -> bool:
stack=[]
for i in s:
if i=='(':
stack.append(')')
elif i=='{':
stack.append('}')
elif i=='[':
stack.append(']')
#为空的情况是右括号多了,有左括号的时候会入栈右括号,此时没有左括号,栈为空,未遍历完字符串,栈就为空了
elif not stack or stack[-1]!=i:
return False
else:
stack.pop()
return not stack10.两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的 交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
实现方法
(1)暴力
python
class Solution(object):
def intersection(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
record=set()
for i in range(len(nums1)):
for j in range(len(nums2)):
if nums1[i]==nums2[j]:
record.add(nums1[i])
return list(record)(2)set
python
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
return list(set(nums1)&set(nums2))(3)数组
python
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
count1=[0]*1001
count2=[0]*1001
result=[]
for i in nums1:
count1[i]+=1
for i in nums2:
count2[i]+=1
#交集只要求元素存在
for i in range(1001):
if count1[i]*count2[i]>0:
#注意返回的是元素的本身,而不是次数
result.append(i)
return result11.买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
实现代码
(1)暴力
python
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
ans=0
for i in range(len(prices)):
for j in range(i+1,len(prices)):
ans=max(ans,prices[j]-prices[i])
return ans(2)一次遍历
要寻求最大的利润,一定是最低点买入股票,如果我假设第i天卖出,我要获取最大的利润,我必定在i-1天中的最低点买入,所以我依次来遍历,假设每一天都卖出,卖出的时候记录最低价格,那么遍历一次整个股票价格,我就可以得到最大利润。
python
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
maxProfit=0
minprice=int(1e9)
for i in range(len(prices)):
maxProfit=max(maxProfit,prices[i]-minprice)
minprice=min(prices[i],minprice)
return maxProfit基础知识
10分钟彻底搞懂"动态规划"算法_哔哩哔哩_bilibili
求最长递增子序列长度:暴力枚举
python
def L(nums,i):
#递归终止条件,当遍历至最后一个数字,没有子序列
if i==len(nums)-1:
return 1
max_len=1
for j in range(i+1,len(nums)):
if nums[j]>nums[i]:
max_len=max(max_len,L(nums,j)+1)
return max_len
def length_of_LIS(nums):
return max(L(nums,i) for i in range(len(nums)))动态规划,避免重复节点的计算
python
#记录从i开始的最长子序列长度
memo={}
def L(nums,i):
if i in memo:
return memo[i]
#递归终止条件,当遍历至最后一个数字,没有子序列
if i==len(nums)-1:
return 1
max_len=1
for j in range(i+1,len(nums)):
if nums[j]>nums[i]:
max_len=max(max_len,L(nums,j)+1)
memo[i]=max_len
return max_len
def length_of_LIS(nums):
return max(L(nums,i) for i in range(len(nums)))迭代算法
python
def length_of_LIS(nums):
n=len(nums)
L=[1]*n
for i in reversed(range(n)):
for j in range(i+1,n):
if nums[j]>nums[i]:
L[i]=max(L[i],L[j]+1)
return max(L)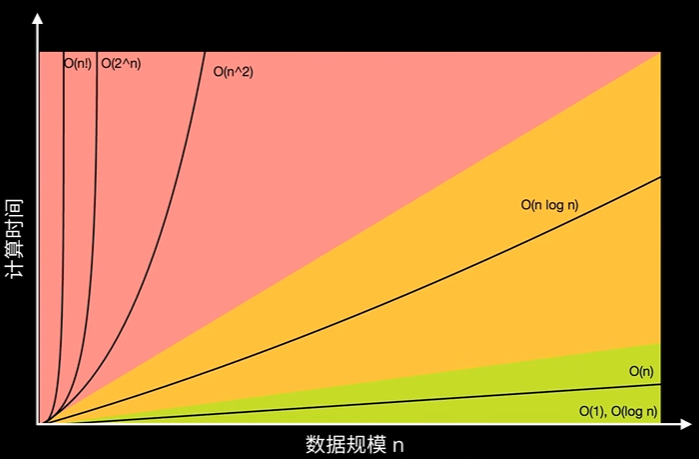
12.只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
实现方法
(1)集合
使用集合存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字
python
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
num_set=set()
for i in nums:
if i not in num_set:
num_set.add(i)
else:
num_set.remove(i)
return num_set.pop()(2)哈希表
使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。
python
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
dict={}
for i in nums:
dict[i]=dict.get(i,0)+1
for num,count in dict.items():
#items() 是字典的内置方法,会返回一个包含所有键值对的可迭代对象,每个元素是一个元组 (数字, 次数)
if count==1:
return num(3)集合技巧
使用集合存储数组中出现的所有数字,并计算数组中的元素之和。由于集合保证元素无重复,因此计算集合中的所有元素之和的两倍,即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次,其余元素都出现两次,因此用集合中的元素之和的两倍减去数组中的元素之和,剩下的数就是数组中只出现一次的数字。
python
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
unique_nums=set(nums)
double_nums=2*sum(unique_nums)
return double_nums-sum(nums)(4)位运算
python
class Solution(object):
def singleNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return reduce(lambda x,y:x^y,nums)基础知识
(1)当算法的空间复杂度为O(1)时,称为 "常数空间复杂度"。它表示算法所需的额外存储空间不随输入规模n变化,始终是一个固定的常量。
(2)当算法的时间复杂度为O(n)时,称为 "线性时间复杂度"。它表示算法的执行时间与输入规模n成正比例关系。
(3)异或运算有以下三个性质:任何数和 0 做异或运算,结果仍然是原来的数,即 a⊕0=a 。
任何数和其自身做异或运算,结果是 0,即 a⊕a=0。异或运算满足交换律和结合律,即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。
13.多数元素
给定一个大小为 n的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
实现方法
(1)哈希表
时间复杂度O(n),空间复杂度O(n)
python
class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
counts = collections.Counter(nums)
return max(counts.keys(), key=counts.get)(2)排序
时间复杂度:O(nlogn)。将数组排序的时间复杂度为 O(nlogn)
空间复杂度:O(logn)。如果使用语言自带的排序算法,需要使用 O(logn) 的栈空间。如果自己编写堆排序,则只需要使用 O(1) 的额外空间。
如果将nums中的所有元素按照单调递增或者单调递减的顺序,那么 ⌊ n/2 ⌋ 的元素一定是个众数。
python
class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums.sort()
return nums[len(nums)//2]基础知识
(1) collections:是 Python 标准库中的一个模块,提供了一些额外的「容器数据类型」(比内置的 list/dict 更特殊的结构)。
(2 collections 模块中的一个类,专门用于计数 ------ 它会接收一个可迭代对象(比如列表 nums),然后返回一个**「类似字典」**的对象,其中:)如果 nums = [3, 2, 3, 1, 3],那么 counts 会是:Counter({3: 3, 2: 1, 1: 1})
14.移除元素
给你一个数组 nums和一个值 val,你需要 原地 移除所有数值等于 val的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。 - 返回
k。
实现代码
python
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
j=0
for i in range(len(nums)):
if nums[i]!=val:
nums[j]=nums[i]
j=j+1
return j15.有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
实现方法
python
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
k=len(nums)-1
i=0
j=len(nums)-1
res=[float('inf')]*len(nums)
while i<=j:
if nums[i]**2<nums[j]**2:
res[k]= nums[j]**2
k=k-1
j=j-1
else:
res[k]= nums[i]**2
k=k-1
i=i+1
return res16.长度最小的子数组
给定一个含有 n个正整数的数组和一个正整数 target。
找出该数组中满足其总和大于等于target的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。** 如果不存在符合条件的子数组,返回 0 。
实现方法
(1)暴力
python
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
n=len(nums)
ans=n+1
for i in range(n):
total=0
for j in range(i,n):
total=total+nums[j]
if total>=target:
ans=min(ans,j-i+1)
break
if ans==n+1:
return 0
else:
return ans(2)滑动窗口
python
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
minLen=len(nums)+1
i=0
sum=0
for j in range(len(nums)):
sum=sum+nums[j]
while sum>=target:
minLen=min(minLen,j-i+1)
sum=sum-nums[i]
i=i+1
if minLen==len(nums)+1:return 0
return minLen思路:元素abcde 下标01234 先想暴力怎么做?
固定左端点枚举右端点 以0下标为左端点的子数组:a ab abc abcd abcde 以1下标为左端点的子数组:b bc bcd bced 以2、以3... 可以把所有子数组都找到 枚举过程中求和,如果sum≥target就拿当前的子数组长度和ans求最小 时间复杂度O(n^2)
尝试优化 因为元素都为正数并且是求最小长度 假设a+b+c<target,a+b+c+d≥target,那a+b+c+d+e也一定≥target,所以无需继续累加,a为左端点符合要求的最短子数组长度就是4,当sum≥=target时直接break 继续枚举下一个左端点 时间复杂度O(n^2)
最终优化 假设a+b+c<target,a+b+c+d≥target 我们知道了a为左端点符合要求最短子数组长度为4, 接着枚举b为左端点的子数组时,暴力是从b开始重新累加的,其实没有必要,因为a+b+c<target,所以b一定<target,b+c也一定<target,所以我们接着从上次a+b+c+d的和减去a继续进行就好,如果b+c+d的和≥target,以b为左端点最短就是3,不是就接着累加下一个数,直到没有数可累加时结束 时间复杂度O(n)
这就是为什么暴力那个指针不退回的原理,本质就是利用数据的单调性过滤掉sum≥target长度太长和sum<target的子数组来优化暴力
17.爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
实现代码:
python
class Solution:
def climbStairs(self, n: int) -> int:
if n<3:return n
f1=1
f2=2
for _ in range(3,n+1):
sum=f1+f2
f1=f2
f2=sum
return f218.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法
实现方法
(1)遍历
时间复杂度不符合要求
python
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
flag=False
for i in range(len(nums)):
if nums[i]==target:
flag=True
return i
if flag==False:
for i in range(len(nums)):
for j in range(i+1,len(nums)):
if target<nums[j] and target>nums[i]:
return j
if target>nums[len(nums)-1]:
return len(nums)(2)二分查找
python
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left=0
right=len(nums)-1
while left<=right:
mid=left+(right-left)//2
if nums[mid]<target:
left=mid+1
else:
right=mid-1
return left
python
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left=-1
right=len(nums)
while left+1<right:
mid=left+(right-left)//2
if nums[mid]<target:
left=mid
else:
right=mid
return right19.在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
实现方法
python
class Solution:
def lower_bound(self, nums: List[int], target: int) -> List[int]:
left=0
right=len(nums)-1
while left<=right:
mid=left+(right-left)//2
if nums[mid]<target:
left=mid+1
else:
right=mid-1
return left
def searchRange(self, nums: List[int], target: int) -> List[int]:
start=self.lower_bound(nums,target)
if start==len(nums) or nums[start]!=target:
return [-1,-1]
end=self.lower_bound(nums,target+1)-1
return [start,end]基础知识
二分查找 红蓝染色法【基础算法精讲 04】_哔哩哔哩_bilibili
二分查找在闭区间、半开半闭区间、区间的三种写法以及>=、<=、>、<四种类型的转换
一般写法是>=x, >转换为>=(x+1), <转化为(>=x)-1 ,<=可以转化为 (>x)-1
20.寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n)的算法来解决此问题。
实现方法
python
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
left=-1
right=len(nums)-1
while left+1<right:
mid=left+(right-left)//2
if nums[mid]>nums[mid+1]:
right=mid
else:
left=mid
return right备注:红蓝染色法:红色表示目标峰顶左侧、蓝色表示目标峰顶或者目的峰顶的右侧
21.寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
实现方法
红色表示最小值左侧、蓝色表示最小值右侧
python
class Solution:
def findMin(self, nums: List[int]) -> int:
left=-1
right=len(nums)-1
while left+1<right:
mid=left+(right-left)//2
if nums[mid]<nums[-1]:
right=mid
else:
left=mid
return nums[right]22.N叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
实现方法
python
class Solution:
def maxDepth(self, root: 'Node') -> int:
if root is None:
return 0
que=collections.deque([root])
size=0
while que:
level_size=len(que)
size=size+1
for _ in range(level_size):
node=que.popleft()
if node.children:
for children in node.children:
que.append(children)
return size23.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
实现方法
python
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
que=collections.deque([root])
size=0
while que:
level_size=len(que)
size=size+1
for _ in range(level_size):
node=que.popleft()
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
if not node.left and not node.right:
return size
return size24.二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
实现方法
(1)递归
树的遍历方法总体分为两类:一类是深度优先遍历(DFS),另一类是广度优先遍历(BFS)。此树的深度和其左(右)子树的深度之间的关系。显然,此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1 。
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:return 0
return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
return self.getHeight(root)
def getHeight(self,node):
if node is None:
return 0
leftHeight=self.getHeight(node.left)
rightHeight=self.getHeight(node.right)
height=1+max(leftHeight,rightHeight)
return height(2)层序遍历
每遍历一层,则计数器 +1 ,直到遍历完成,则可得到树的深度。
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:return 0
queue=[root]
res=0
while queue:
tmp=[]
for node in queue:
if node.left:tmp.append(node.left)
if node.right:tmp.append(node.right)
queue=tmp
res=res+1
return res
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
ans=0
def f(node,cnt):
if node is None:
return
cnt=cnt+1
nonlocal ans
ans=max(ans,cnt)
f(node.right,cnt)
f(node.left,cnt)
f(root,0)
return ans
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
que=collections.deque([root])
size=0
while que:
level_size=len(que)
for _ in range(level_size):
node=que.popleft()
if node.right:
que.append(node.right)
if node.left:
que.append(node.left)
size=size+1
return size25.翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
实现方法
(1)递归
交换当前节点的左右节点,再递归的交换当前节点的左节点,递归的交换当前节点的右节点。节点为null时返回
python
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:return None
root.left,root.right=root.right,root.left
if root.left:
self.invertTree(root.left)
if root.right:
self.invertTree(root.right)
return root(2)迭代
广度优先遍历需要额外的数据结构--队列,来存放临时遍历到的元素。所以,我们需要先将根节点放入到队列中,然后不断的迭代队列中的元素。对当前元素调换其左右子树的位置,然后:判断其左子树是否为空,不为空就放入队列中,判断其右子树是否为空,不为空就放入队列中
python
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:return None
queue=[root]
while queue:
tmp=queue.pop(0)
tmp.left,tmp.right=tmp.right,tmp.left
if tmp.left:
queue.append(tmp.left)
if tmp.right:
queue.append(tmp.right)
return root26.对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
实现代码
python
class Solution:
def isSame(self,p,q):
if p is None or q is None:
return p is q
return p.val==q.val and self.isSame(p.right,q.left) and self.isSame(p.left,q.right)
def isSymmetric(self, root: TreeNode) -> bool:
return self.isSame(root.right,root.left)备注:相同的树和对称二叉树都是相当于判断两个子树是否相同。
27.相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
实现方法
python
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if p is None or q is None:
return p is q
return p.val==q.val and self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)28.平衡二叉树
给定一个二叉树,判断它是否是 平衡二叉树
实现方法
(1)自顶而下的递归
有了计算节点高度的函数(二叉树的最大深度),即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历,即对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过 1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。
python
class Solution:
def depth(self,node):
if node is None:
return 0
return max(self.depth(node.right),self.depth(node.left))+1
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
return abs(self.depth(root.left)-self.depth(root.right))<=1 and self.isBalanced(root.left) and self.isBalanced(root.right)(2)自底而上的递归
自底向上递归的做法类似于后序遍历,**对于当前遍历到的节点,先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的,则返回其高度(高度一定是非负整数),否则返回 −1。**如果存在一棵子树不平衡,则整个二叉树一定不平衡。
python
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def getHeight(node):
if node is None:
return 0
left=getHeight(node.left)
right=getHeight(node.right)
if left==-1 or right==-1 or abs(left-right)>1:
return -1
return max(left,right)+1
return getHeight(root)!=-1基础知识
二叉树的每个节点的左右子树的高度差的绝对值不超过 1,则二叉树是平衡二叉树。根据定义,一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此可以使用递归的方式判断二叉树是不是平衡二叉树,递归的顺序可以是自顶向下或者自底向上。
29.螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
实现方法
python
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix=[[0]*n for _ in range(n)]
col,row=0,0
offset=1
count=1
mid=n//2
iteration=n//2
for offset in range(1,iteration+1):
for j in range(col,n-offset):
matrix[row][j]=count
count=count+1
for i in range(row,n-offset):
matrix[i][n-offset]=count
count=count+1
for j in range(n-offset,col,-1):
matrix[n-offset][j]=count
count=count+1
for i in range(n-offset,row,-1):
matrix[i][col]=count
count=count+1
col=col+1
row=row+1
if n%2==1:matrix[mid][mid]=n**2
return matrix
30.移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
实现方法
(1)原链表删除元素
python
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
while head and head.val==val:
head=head.next
p=head
while p and p.next:
if p.next.val==val:
p.next=p.next.next
else:
p=p.next
#注意最后返回的是head不是p
return head(2)使用虚拟头节点
python
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
dummy_head=ListNode(next=head)
cur=dummy_head
while cur.next:
if cur.next.val==val:
cur.next=cur.next.next
else:
cur=cur.next
return dummy_head.next
#注意返回31.设计链表
你可以选择使用单链表或者双链表,设计并实现自己的链表。
单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。
如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
实现 MyLinkedList 类:
MyLinkedList()初始化MyLinkedList对象。int get(int index)获取链表中下标为index的节点的值。如果下标无效,则返回-1。void addAtHead(int val)将一个值为val的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。void addAtTail(int val)将一个值为val的节点追加到链表中作为链表的最后一个元素。void addAtIndex(int index, int val)将一个值为val的节点插入到链表中下标为index的节点之前。如果index等于链表的长度,那么该节点会被追加到链表的末尾。如果index比长度更大,该节点将 不会插入 到链表中。void deleteAtIndex(int index)如果下标有效,则删除链表中下标为index的节点。
实现方法
python
class MyLinkedList:
def __init__(self):
self.dummy_head=ListNode()
self.size=0
def get(self, index: int) -> int:
cur=self.dummy_head.next
if index<0 or index>=self.size:return -1
for i in range(index):
cur=cur.next
return cur.val
def addAtHead(self, val: int) -> None:
self.dummy_head.next=ListNode(val,self.dummy_head.next)
self.size=self.size+1
def addAtTail(self, val: int) -> None:
cur=self.dummy_head
while cur.next:
cur=cur.next
cur.next=ListNode(val)
self.size=self.size+1
def addAtIndex(self, index: int, val: int) -> None:
if index<0 or index>self.size:return
cur=self.dummy_head
for i in range(index):
cur=cur.next
cur.next=ListNode(val,cur.next)
self.size=self.size+1
def deleteAtIndex(self, index: int) -> None:
if index<0 or index>=self.size:return
cur=self.dummy_head
for i in range(index):
cur=cur.next
cur.next=cur.next.next
self.size=self.size-132.两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
实现代码
python
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
dummy_head=ListNode(next=head)
cur=dummy_head
while cur.next and cur.next.next:
tmp1=cur.next
tmp3=cur.next.next.next
cur.next=cur.next.next
cur.next.next=tmp1
tmp1.next=tmp3
cur=tmp1
return dummy_head.next33.删除链表的倒数第N个节点
给你一个链表,删除链表的倒数第 n个结点,并且返回链表的头结点。
实现方法:
python
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy_head=ListNode(next=head)
cur1=dummy_head
count=0
while cur1.next:
count=count+1
cur1=cur1.next
cur2=dummy_head
for i in range(count-n):
cur2=cur2.next
cur2.next=cur2.next.next
return dummy_head.next
python
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy_head=ListNode(next=head)
fast=slow=dummy_head
count=0
for i in range(n+1):
fast=fast.next
while fast:
fast=fast.next
slow=slow.next
slow.next=slow.next.next
return dummy_head.next34.环形链表II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始 )。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改链表。
实现方法:
python
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
fast=slow=head
while fast and fast.next:
fast=fast.next.next
slow=slow.next
if fast==slow:
index=head
while fast!=index:
fast=fast.next
index=index.next
return index
return None35.四数之和
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
python
class Solution:
def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:
dict={}
for i in nums1:
for j in nums2:
if i+j in dict:
dict[i+j]+=1
else:
dict[i+j]=1
count=0
for k in nums3:
for l in nums4:
target=0-k-l
if target in dict:
count+=dict[target]
return count基础知识
rec = defaultdict(lambda : 0):创建一个defaultdict,其「默认工厂函数」是lambda: 0(即当访问不存在的键时,自动赋值为 0)
36.三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
实现方法
python
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result=[]
#记得排序啊
nums.sort()
for i in range(len(nums)):
if nums[i]>0:
return result
if i>0 and nums[i]==nums[i-1]:
continue
left=i+1
right=len(nums)-1
while left<right:
sum=nums[i]+nums[left]+nums[right]
if sum>0:
right-=1
elif sum<0:
left+=1
else:
result.append([nums[i],nums[left],nums[right]])
while left<right and nums[left]==nums[left+1]:
left+=1
while left<right and nums[right]==nums[right-1]:
right-=1
left+=1
right-=1
return result37.四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复 的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
实现方法
python
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
result=[]
nums.sort()
for i in range(len(nums)):
if nums[i]>target and target>0:
break
if i>0 and nums[i]==nums[i-1]:
continue
for j in range(i+1,len(nums)):
if nums[i]+nums[j]>target and target>0:
break
if j>i+1 and nums[j]==nums[j-1]:
continue
left=j+1
right=len(nums)-1
while left<right:
sum=nums[i]+nums[j]+nums[left]+nums[right]
if sum>target:
right-=1
elif sum<target:
left+=1
else:
result.append([nums[i],nums[j],nums[left],nums[right]])
while left<right and nums[left]==nums[left+1]:
left+=1
while left<right and nums[right]==nums[right-1]:
right-=1
left+=1
right-=1
return result 38.反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
实现方法
python
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
left, right = 0, len(s) - 1
# 该方法已经不需要判断奇偶数,经测试后时间空间复杂度比用 for i in range(len(s)//2)更低
# 因为while每次循环需要进行条件判断,而range函数不需要,直接生成数字,因此时间复杂度更低。推荐使用range
while left < right:
s[left], s[right] = s[right], s[left]
left += 1
right -= 1
39.反转字符串II
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k个,则将剩余字符全部反转。 - 如果剩余字符小于
2k但大于或等于k个,则反转前k个字符,其余字符保持原样。
实现方法
python
class Solution:
def reverseStr(self, s: str, k: int) -> str:
def reverse_substring(text):
left,right=0,len(text)-1
while left<right:
text[left],text[right]=text[right],text[left]
left+=1
right-=1
#注意要有返回值
return text
strs=list(s)
for i in range(0,len(strs),2*k):
strs[i:i+k]=reverse_substring(strs[i:i+k])
return "".join(strs)备注:切片会自动适配(超范围时取到列表末尾)
基础知识
Python 中的字符串是不可变对象,不能直接修改其中的某个字符(比如s[0] = 'H'会报错)。而列表是可变对象,可以直接修改其中的元素,这为我们提供了修改字符的可能性
python
s = "hello"
res = list(s)
print(res) # 输出: ['h', 'e', 'l', 'l', 'o']列表转换回字符串
python
res = ['h', 'e', 'l', 'l', 'o']
s = ''.join(res)
print(s) # 输出: "hello"
python
res = ['a', 'b', 'c', 'd', 'e']
print(res[1:3]) # 输出: ['b', 'c'] (包含索引1,不包含索引3)40.反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意: 输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
实现方法
python
class Solution:
def reverseWords(self, s: str) -> str:
words=s.split()
words=words[::-1]
#join后面没有小数点
return ' '.join(words)
python
class Solution:
def reverseWords(self, s: str) -> str:
s=s[::-1]
return ' '.join(words[::-1] for words in s.split())
python
class Solution:
def reverseWords(self, s: str) -> str:
words=s.split()
left=0
right=len(words)-1
while left<right:
words[left],words[right]=words[right],words[left]
left+=1
right-=1
return " ".join(words)
python
class Solution:
# 别缺少self参数
def singlereverse(self,s,start,end):
while start<end:
s[start],s[end]=s[end],s[start]
start+=1
end-=1
def reverseWords(self, s: str) -> str:
s=list(s)
s.reverse()
fast=0
slow=0
#去除多余的空格
while fast<len(s):
if s[fast]!=" ":
if slow!=0:
s[slow]=" "
slow+=1
while fast<len(s) and s[fast]!=" ":
s[slow]=s[fast]
fast+=1
##注意是slow++1
slow+=1
else:
fast+=1
slow1=0
fast1=0
#截断列表,保留列表中从开始到 slow-1 索引的有效元素
#交换单个单词的顺序,注意长度变化,不能使用n
s = s[:slow]
while fast1<=len(s):
if fast1==len(s) or s[fast1]==" " :
#注意是fast-1
self.singlereverse(s,slow1,fast1-1)
slow1=fast1+1
fast1+=1
else:
fast1+=1
return "".join(s)
41.用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
实现代码
python
class MyQueue:
def __init__(self):
self.stack_in=[]
self.stack_out=[]
#注意别丢掉self
def push(self, x: int) -> None:
self.stack_in.append(x)
def pop(self) -> int:
if self.empty():
return None
if self.stack_out:
return self.stack_out.pop()
else:
for i in range(len(self.stack_in)):
self.stack_out.append(self.stack_in.pop())
return self.stack_out.pop()
def peek(self) -> int:
ans=self.pop()
self.stack_out.append(ans)
return ans
def empty(self) -> bool:
return not (self.stack_in or self.stack_out)42.用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
实现方法
python
class MyStack:
def __init__(self):
self.que=deque()
def push(self, x: int) -> None:
self.que.append(x)
def pop(self) -> int:
if self.empty():
return None
for i in range(len(self.que)-1):
self.que.append(self.que.popleft())
return self.que.popleft()
def top(self) -> int:
if not self.que:
return None
return self.que[-1]
def empty(self) -> bool:
return not self.que43.删除字符串中所有相邻重复项
给出由小写字母组成的字符串 s,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 s 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
实现方法
python
class Solution:
def removeDuplicates(self, s: str) -> str:
stack=[]
for item in s:
if stack and stack[-1]==item:
stack.pop()
else:
stack.append(item)
return "".join(stack)44.逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
实现代码
python
from operator import add,sub,mul
#div 定义在类外时,属于全局作用域。
def div(x,y):
return x//y if x*y>0 else -(abs(x)//abs(y))
class Solution:
dict1={'+':add,'-':sub,'*':mul,'/':div}
def evalRPN(self, tokens: List[str]) -> int:
stack=[]
for token in tokens:
#{'+', '-', '*', '/'}可以与self.dict1相互进行替换
if token not in self.dict1:
#数字注意转换类型
stack.append(int(token))
else:
num1=stack.pop()
num2=stack.pop()
#先出来的数字在后面那一个
stack.append(self.dict1[token](num2,num1))
return stack.pop()递归三部曲
1.确定递归函数的参数和返回值
2.确定终止条件
3.确定单层的递归逻辑
45.二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
实现方法
(1)递归
时间复杂度O(n),空间复杂度O(h),h是树的高度
python
class Solution(object):
def inorderTraversal(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[int]
"""
res=[]
def dfs(root):
if not root:
return
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
return res(2)迭代
用「栈」来模拟递归过程,
python
class Solution(object):
def inorderTraversal(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[int]
"""
stack=[root]
res=[]
while stack:
i=stack.pop()
if isinstance(i,TreeNode):
stack.extend([i.right,i.val,i.left])
elif isinstance(i,int):
res.append(i)
return res
python
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
res=[]
stack=[]
cur=root
while cur or stack:
if cur:
#中序遍历的非递归实现中,栈应该存储节点对象而不是节点的值,否则后续无法通过弹出的元素访问其右子树
stack.append(cur)
cur=cur.left
else:
cur=stack.pop()
res.append(cur.val)
cur=cur.right
return res(3)二叉树的前序遍历
python
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res=[]
def dfs(root):
if root is None:
return
res.append(root.val)
dfs(root.left)
dfs(root.right)
dfs(root)
return res
python
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
stack=[root]
res=[]
while stack:
node=stack.pop()
res.append(node.val)
#迭代方式注意顺序相反
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res(4)二叉树的后序遍历
python
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res=[]
def dfs(root):
if root is None:
return
dfs(root.left)
dfs(root.right)
res.append(root.val)
dfs(root)
return res
python
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
stack=[root]
res=[]
while stack:
node=stack.pop()
res.append(node.val)
#迭代方式注意顺序相反
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return res[::-1]基础知识
1.二叉树节点的类 TreeNode
python
class TreeNode(object):
def _init_(self,val=0,left=None,right=None):
self.val=val
self.right=right
self.left=left46.二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
实现代码
python
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
que=collections.deque([root])
result=[]
while que:
level=[]
for _ in range(len(que)):
node=que.popleft()
level.append(node.val)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
result.append(level)
return result 47.二叉树的层序遍历Ⅱ
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
实现代码
python
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
que=collections.deque([root])
result=[]
while que:
level=[]
for _ in range(len(que)):
node=que.popleft()
level.append(node.val)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
result.append(level)
return result[::-1]48.二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
备注:层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
实现方法
python
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
que=collections.deque([root])
result=[]
while que:
level_size=len(que)
for i in range(level_size):
node=que.popleft()
#要判断每一层的最后一个节点,所以要固定长度
if i==level_size-1:
result.append(node.val)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return result49.二叉树的平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
实现代码
python
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
que=collections.deque([root])
result=[]
while que:
level_size=len(que)
level_sum=0
for i in range(level_size):
node=que.popleft()
level_sum=level_sum+node.val
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
aver=level_sum/level_size
result.append(aver)
return result50.N叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
实现代码
python
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if root is None:
return []
que=collections.deque([root])
result=[]
while que:
level=[]
for _ in range(len(que)):
node=que.popleft()
level.append(node.val)
for children in node.children:
que.append(children)
result.append(level)
return result 51.在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
实现代码
python
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
que=collections.deque([root])
result=[]
while que:
level_max=-inf
for _ in range(len(que)):
node=que.popleft()
level_max=max(node.val,level_max)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
result.append(level_max)
return result52.填充每个节点的下一个右侧节点指针
python
给定一个完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。实现代码
python
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if root is None:
return root
que=collections.deque([root])
while que:
level_size=len(que)
prev=None
for _ in range(level_size):
node=que.popleft()
if prev:
prev.next=node
prev=node
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return root53.填充每个节点的下一个右侧节点指针Ⅱ
python
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。实现代码
python
class Solution:
def connect(self, root: 'Node') -> 'Node':
if root is None:
return root
que=collections.deque([root])
while que:
pre=None
level_size=len(que)
for _ in range(level_size):
node=que.popleft()
if pre:
pre.next=node
pre=node
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return root