【深度学习|学习笔记】详细讲解一下 深度学习训练过程中 为什么 Momentum 可以加速训练?
【深度学习|学习笔记】详细讲解一下 深度学习训练过程中 为什么 Momentum 可以加速训练?
文章目录
- [【深度学习|学习笔记】详细讲解一下 深度学习训练过程中 为什么 Momentum 可以加速训练?](#【深度学习|学习笔记】详细讲解一下 深度学习训练过程中 为什么 Momentum 可以加速训练?)
-
- [1. 普通 SGD 的问题](#1. 普通 SGD 的问题)
- [2. Momentum 的思想](#2. Momentum 的思想)
- [3. 直观理解](#3. 直观理解)
- [4. 代码示例(PyTorch 对比 SGD 和 SGD+Momentum)](#4. 代码示例(PyTorch 对比 SGD 和 SGD+Momentum))
- [5. 总结](#5. 总结)
欢迎铁子们点赞、关注、收藏!
祝大家逢考必过!逢投必中!上岸上岸上岸!upupup
大多数高校硕博生毕业要求需要参加学术会议,发表EI或者SCI检索的学术论文会议论文。详细信息可扫描博文下方二维码 "
学术会议小灵通"或参考学术信息专栏:https://blog.csdn.net/2401_89898861/article/details/148877490
1. 普通 SGD 的问题
- 在随机梯度下降(SGD)中 ,每一步更新参数都依赖于当前梯度方向:
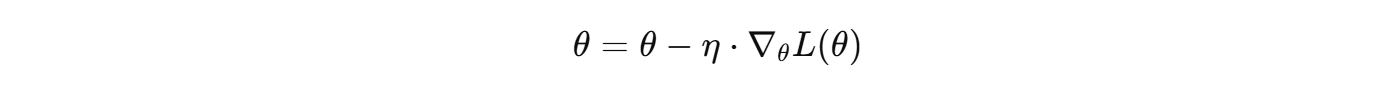
问题: - 在损失函数曲面陡峭的方向(如纵向坡度大)参数更新会来回震荡。
- 在平缓方向(如横向坡度小)更新很慢。
- 因此收敛效率低,特别是在高维空间或峡谷状的损失函数中。
2. Momentum 的思想
- Momentum(动量)引入了"惯性"的概念,相当于在更新时不仅考虑当前梯度,还考虑之前的更新方向:
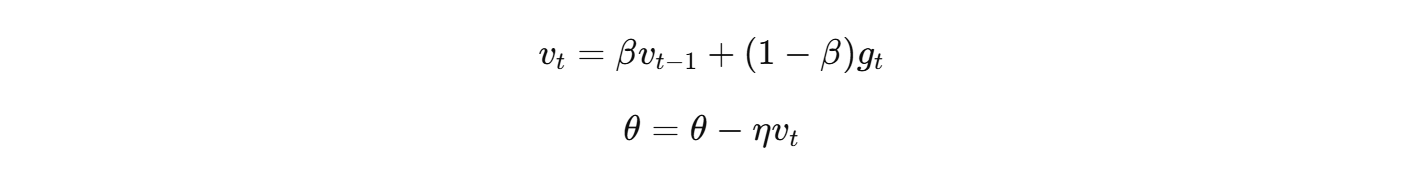
其中: - v t v_t vt:累积的梯度方向(带记忆)
- β β β:动量系数(一般取 0.9)
- g t g_t gt:当前梯度
效果:
- 在梯度方向一致的维度上,动量会不断累积,加速收敛。
- 在梯度方向来回震荡的维度上,动量会抵消抖动,减少震荡。
3. 直观理解
可以把 Momentum 想象成 小球在曲面上滚动:
- 普通 SGD 就像小球只看当前的坡度,走一步停一下。
- Momentum 像是小球有惯性,可以顺着方向滚下去,因此更快更平滑。
4. 代码示例(PyTorch 对比 SGD 和 SGD+Momentum)
我们用一个简单的二次函数 f ( x , y ) = x 2 + 10 y 2 f(x,y)=x^2+10y^2 f(x,y)=x2+10y2 来演示:
- 这个函数在 y 方向比 x 方向陡峭,普通 SGD 会震荡很大,而 Momentum 可以快速收敛。
csharp
import torch
import matplotlib.pyplot as plt
# 定义损失函数 f(x, y) = x^2 + 10y^2
def loss_fn(params):
x, y = params
return x**2 + 10*y**2
# SGD 更新
def sgd_update(params, lr=0.1):
grads = torch.autograd.grad(loss_fn(params), params, create_graph=False)
with torch.no_grad():
for p, g in zip(params, grads):
p -= lr * g
return params
# SGD + Momentum 更新
class SGD_Momentum:
def __init__(self, params, lr=0.1, beta=0.9):
self.params = params
self.lr = lr
self.beta = beta
self.v = [torch.zeros_like(p) for p in params]
def step(self):
grads = torch.autograd.grad(loss_fn(self.params), self.params, create_graph=False)
with torch.no_grad():
for i, (p, g) in enumerate(zip(self.params, grads)):
self.v[i] = self.beta * self.v[i] + (1 - self.beta) * g
p -= self.lr * self.v[i]
return self.params
# 初始化参数
params_sgd = [torch.tensor(5.0, requires_grad=True), torch.tensor(5.0, requires_grad=True)]
params_momentum = [torch.tensor(5.0, requires_grad=True), torch.tensor(5.0, requires_grad=True)]
momentum_opt = SGD_Momentum(params_momentum, lr=0.1, beta=0.9)
# 记录轨迹
sgd_trace, momentum_trace = [], []
for _ in range(50):
sgd_trace.append([p.item() for p in params_sgd])
momentum_trace.append([p.item() for p in params_momentum])
params_sgd = sgd_update(params_sgd, lr=0.1)
momentum_opt.step()
# 可视化
sgd_trace = torch.tensor(sgd_trace)
momentum_trace = torch.tensor(momentum_trace)
plt.plot(sgd_trace[:,0], sgd_trace[:,1], 'o-', label="SGD")
plt.plot(momentum_trace[:,0], momentum_trace[:,1], 'o-', label="SGD+Momentum")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.title("SGD vs SGD+Momentum Trajectories")
plt.show()结果解释
- SGD:在 y 方向来回震荡,收敛慢。
- SGD+Momentum:更新更平滑,能快速向最低点靠拢。
5. 总结
- Momentum 加速训练,是因为它利用了"历史梯度"来平滑更新,减少震荡,并在一致方向上加快收敛。
- 在实践中,SGD + Momentum 已经成为深度学习最常用的优化器之一(很多时候比 Adam 泛化更好)。