卷积神经网络
观察一下左半图(传统神经网络)和右半图(卷积神经网络),
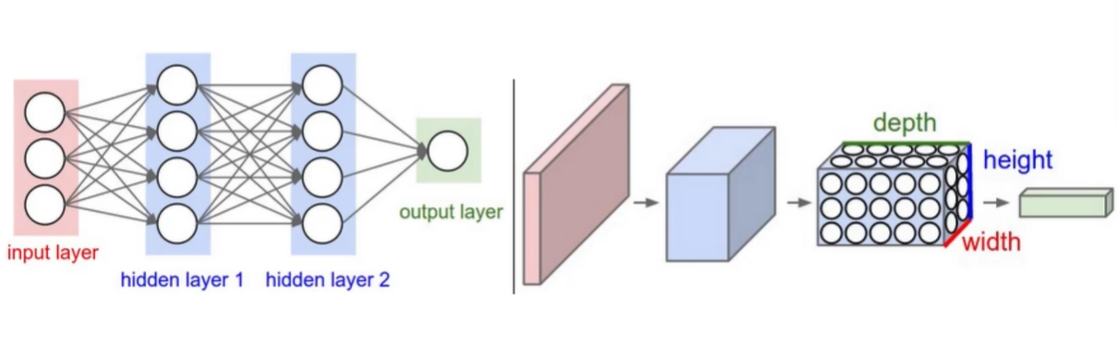
观察一下,感觉有点不同,左边的像是个二维的,右边的像是个三维的...
左边的输入就是 784 个像素点 ,右边的输入不再是像素点,而就是 一张 28 * 28 * 1 的图像 ,所以用 卷积,需要把数据抬高一个维度 ,不再是一列特征,而是一个长方体矩阵,是一个 h * w * c 的数据,不会把这个数据拉成一个向量,而是直接对这个样本数据进行特征提取。
整体架构:输入层、卷积层、池化层、全连接层。

数一数,这个架构有几层?
- 提示一:其中 Conv 和 ReLU 基本上是一个组合,
- 提示二:只有有权重参数矩阵要更新的,才叫做 层,
所以说,激活函数 ReLU 没有参数更新,池化也没有参数更新,都不算层,
两个卷积一个池化,总共三组,最后加上一个全连接层,也就是 2 × 3 + 1 = 7 2 \times 3 + 1 = 7 2×3+1=7 层。
特征图的变化一般是:
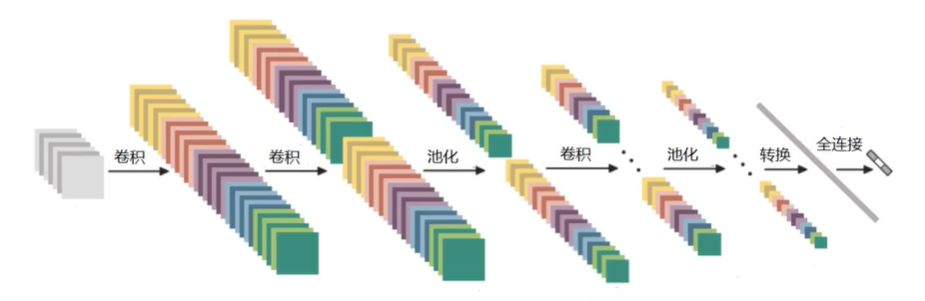
假设输入是 32 * 32 * 3,经过一次卷积,特征图个数明显增多,再经过一次卷积,特征图个数又多了,做个池化吧,它的体积变小了,... 最后拉长成一个特征向量,经过全连接层得到分类结果。
卷积层(特征提取)
比如一张喵喵的图像,不同区域的特征是不同的,比如眼睛、鼻子、嘴巴、须须。
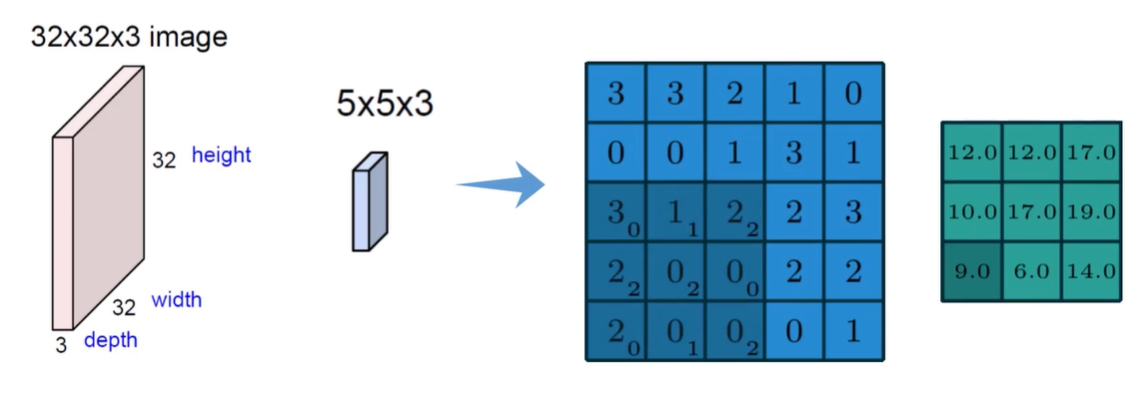
所以就把原始图像划分为多个块块,比如 3 * 3 大小划分块,对于当前这个块,是要选出来特征值。
怎么选?在神经网络中是 用一组权重参数(卷积核)来提取特征。
具体怎么提取,参考 【卷积神经网络】卷积的理解,卷积与通道的关系
只做一次卷积就可以了吗?

做一次卷积是不够的,是在上一次卷积后得到的特征图上,继续做卷积,每一层会学习不同层次的特征,详见 扩展知识。
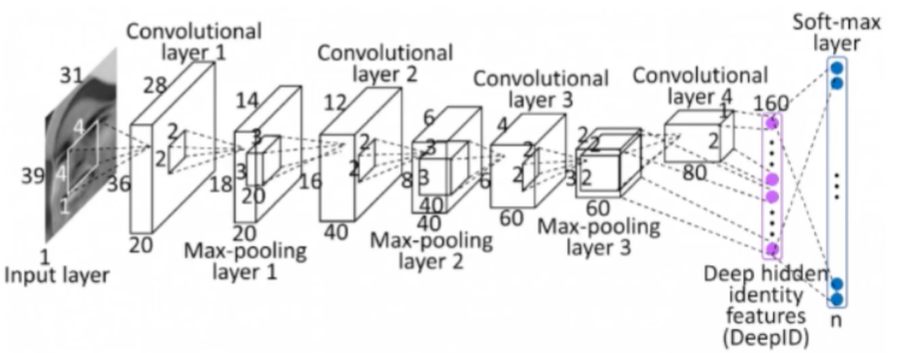
滑动窗口步长
移动窗口可以移动大一点、小一点。
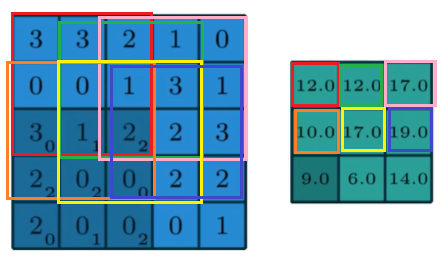
步长为 1 的卷积,绿色在红色的基础上向右移动了一个单元格,
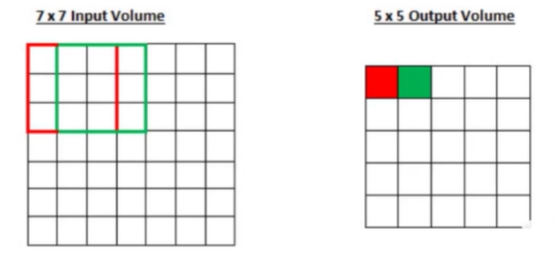
步长为 2 的卷积,移动两个单元格,
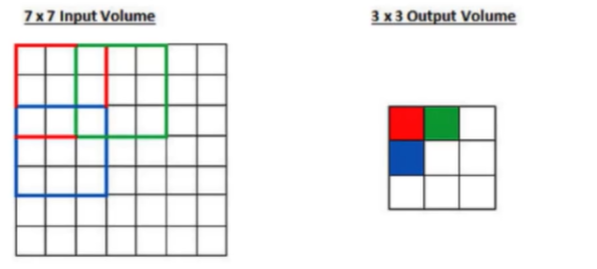
看结果,
- 当步长小的时候,相当于 慢慢地、细粒度地提取特征 ,这样 得到的特征比较丰富;
- 当步长大的时候,走地 比较粗糙 ,滑动比较大,得到的特征比较少,没有那么丰富。
对于图像来说,通常选择步长为 1。
对于文本任务,比如 2 个词一滑动 3 个词一滑动,因为 步长为 1 的时候,得到的特征多,计算效率低。
卷积核尺寸
相当于选择区域大小不同,比如卷积核 3 * 3 得到一个值,4 * 4 得到一个值。
卷积核比较小,也是越细粒度地提取;卷积核比较大,也是比较粗糙地提取。
基本做法是,步长比较小一般是 1,卷积核一般是 3 *3,这是比较常见的。
边缘填充
卷积核滑动时候,有些点被滑动到的次数多,比如中间的那些点,有些点被滑动到的次数少,比如边缘那些点,
但不一定边缘的就一定不重要,那怎么提高边缘点的利用呢?
比如在输入的外围填一圈 0(叫做 zero padding,这个填充值是 0 不会造成负面影响),
那么原来是边界的点就会被滑动到的次数更多,这就是 padding 的作用,让网络更公平地对待边缘的特征。
卷积核个数
这要看最终在计算时,要得到几个特征图。
卷积计算结果
无空洞卷积后输出的空间尺寸 (Height × Width) 由以下因素共同决定:
| 参数 | 含义 |
|---|---|
| H i n , W i n H_{in}, W_{in} Hin,Win | 输入高、宽 |
| k k k | 卷积核尺寸(一般 k × k k×k k×k) |
| s s s | 步幅 stride |
| p p p | 填充 padding |
单维度输出大小为:
H o u t = H i n + 2 p − k s + 1 H_{out} = \frac{H_{in} + 2p - k}{s} + 1 Hout=sHin+2p−k+1
宽度同理。
卷积参数量怎么计算?权重由以下因素决定:
| 参数 | 含义 |
|---|---|
| k k k | 卷积核大小 |
| C i n C_{in} Cin | 输入通道数 |
| C o u t C_{out} Cout | 输出通道数(卷积核个数) |
卷积层参数量公式:
P a r a m s = ( k ⋅ k ⋅ C i n ) ⋅ C o u t Params = (k \cdot k \cdot C_{in})\cdot C_{out} Params=(k⋅k⋅Cin)⋅Cout
举个例子,输入: ( 224 × 224 × 3 ) (224 × 224 × 3) (224×224×3),卷积:
(k=3, s=1, p=1, C_{out}=64),那么输出尺寸:
H o u t = 224 + 2 ⋅ 1 − 3 1 + 1 = 224 ⇒ 224 × 224 × 64 H_{out} = \frac{224 + 2\cdot1 - 3}{1} + 1 = 224 \Rightarrow 224 \times 224 \times 64 Hout=1224+2⋅1−3+1=224⇒224×224×64参数量:
( 3 ⋅ 3 ⋅ 3 ) ⋅ 64 + 64 = 1792 (3\cdot3\cdot3)\cdot64 + 64 = 1792 (3⋅3⋅3)⋅64+64=1792
感受野
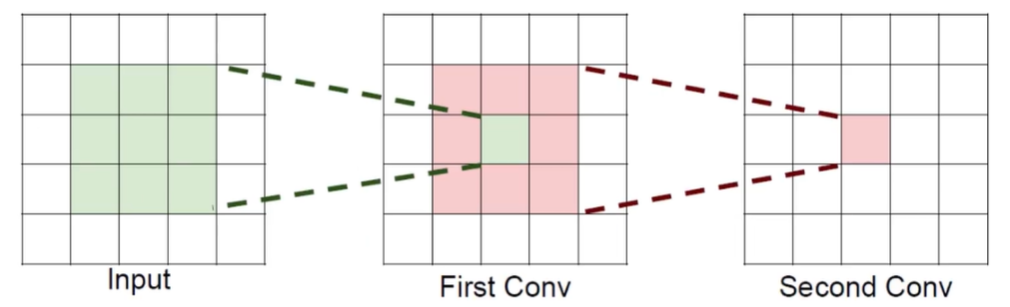
如上图,输入 Input 是 5*5,第一次卷积使用的是 3×3 kernel(绿色为该卷积核覆盖的区域),第二次卷积也是 3×3 kernel(红色为第二层感受的第一层区域),
- 先看
First Conv中的绿色方块 ,对Input绿色区域进行卷积,1 次卷积后得到一个值,也就是First Conv的绿色方块,这个值对应前面的输入应该是3*3大小 ,也就是这个值能看到、感受到前面的大小是3*3; - 再看
First Conv整个红色区域 ,对应前面输入就是5*5,也就是说感受野就是5*5。 - 同理,对于
Second Conv中的红色方块 ,对应了First Conv中的红色区域,也就是它的感受野是5*5。
如果 堆叠 3 个
3*3的卷积层 ,并且保持滑动窗口步长为 1,其感受野就是7*7的了,这跟 一个使用7*7卷积核 的结果是一样的,那为什么非要堆叠 3 个小卷积呢?
假设输入大小都是 h*w*c,并且都使用 c 个卷积核(得到 c 个特征图),可以来计算一下其各自所需参数,
- 1 个
7*7卷积核所需参数: C × ( 7 × 7 × C ) = 49 C 2 C \times (7 \times 7 \times C) = 49 C^2 C×(7×7×C)=49C2 - 3 个
3*3卷积核所需参数: 3 × C × ( 3 × 3 × C ) = 27 C 2 3 \times C \times (3 \times 3 \times C) = 27 C^2 3×C×(3×3×C)=27C2
很明显,堆叠小的卷积核所需的参数更少一些,并且卷积过程越多,特征提取也会越细致,加入的非线性变换也随着增多,还不会增大权重参数个数。
这就是 VGG 网络的基本出发点 ,用 小的卷积核 来完成特征提取操作。
为什么 堆叠 block 会扩大感受野(receptive field, RF)(用公式说明)?
对 1D 卷积,按照常用的分析:
- 单个 conv(
kernel = k,stride = s)把 输入上相邻点的信息融合到一个输出单元上。 - 如果在当前层之前的 累积 stride 是
S,则这个 conv 对原始输入的感受野(增加量)是 ( k − 1 ) × S (k-1)\times S (k−1)×S。
把这些叠加起来,总体(理论)感受野 RF 满足递推关系:
RF new = RF prev + ( k − 1 ) × S prev \text{RF}{\text{new}} = \text{RF}{\text{prev}} + (k-1)\times S_{\text{prev}} RFnew=RFprev+(k−1)×Sprev
其中 S prev S_{\text{prev}} Sprev 是到当前 conv 为止的累积 stride。
对于上图的示例,

两层卷积核 k 1 = k 2 = 3 k_1 = k_2 = 3 k1=k2=3、步幅 s 1 = s 2 = 1 s_1 = s_2 = 1 s1=s2=1、输入层感受野 = 1,
- 第一层卷积: R F 1 = 1 + ( 3 − 1 ) ⋅ 1 = 3 RF_1 = 1 + (3-1)\cdot1 = 3 RF1=1+(3−1)⋅1=3,即:第一层每个输出像素感受野是 3 × 3 3×3 3×3
- 第二层卷积: R F 2 = 3 + ( 3 − 1 ) ⋅ 1 = 5 RF_2 = 3 + (3-1)\cdot1 = 5 RF2=3+(3−1)⋅1=5,即:第二层每个输出像素感受野是 5 × 5 5×5 5×5
| 层 | 感受野大小 |
|---|---|
| 第一层 Conv | 3×3 |
| 第二层 Conv | 5×5 |
所以关键点:堆叠的 conv 每层增加的 RF 是按当前累计下倍数被放大的 。也就是说,越往深层,下采样之前那几层对最终 RF 的贡献越大(成倍放大)。
池化层(特征压缩)
假设卷积得到的结果是下面这样,224 * 224 * 64,这也太大了,得到的特征值太大了,但是这些特征都非常重要吗?未必。
池化层,就是做特征压缩的。经过 pool,变成了 112 * 112 * 64,像是做了瘦身,选择了一些不重要的特征丢弃了,怎么做呢?
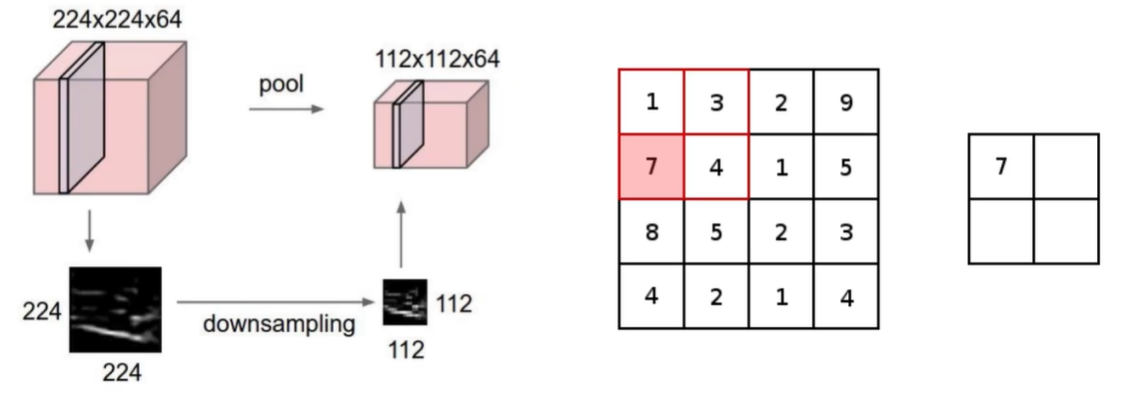
在下面红色框中,做了最大池化 Maxpool,就是选择了一个最大值,最重要的特征保留,其他舍弃。
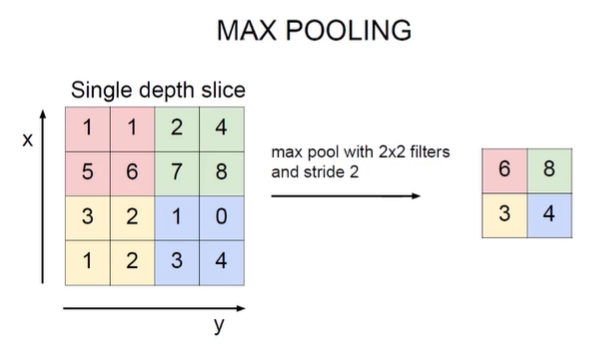
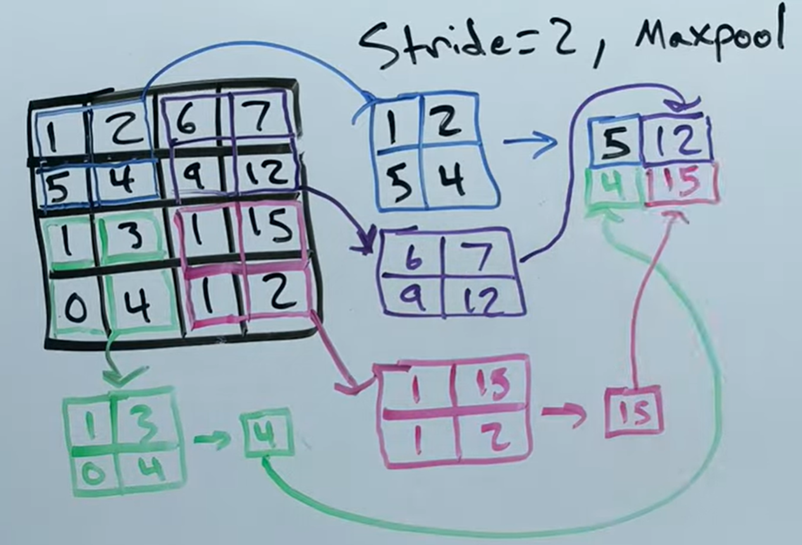
同样是滑动卷积核,但 池化没有权重,只是一个筛选过滤没有计算。而是在每个有效位置上进行操作并返回单个值作为输出,两个常见的操作是取最大值和取平均值。
常见是最大池化,基本上在所有问题中都比平均池化要好,因为已经知道最好的特征了,为什么还要平均一下拉低这个特征呢?
全连接层
假设对于一个分类任务,前面的卷积和池化得到的结果是 32 * 32 * 3,但这是提取的特征的结果,最后还要分类呀?
假设 5 分类,全连接层的输出是五个概率值,那前面的特征图 32 * 32 * 3 得拉长成一个特征向量 吧,再输入到全连接层,把特征转成各分类的概率。
扩展:反卷积网络------可视化每一层提取的特征
论文《Visualizing and Understanding Convolutional Networks》提供了一种有效的方法,来 可视化和理解卷积网络的内部工作机制,从而帮助我们设计和改进网络模型。
其中介绍的一种用于可视化和理解卷积网络的技术,叫做 反卷积网络 (Deconvnet)。反卷积网络是一种与卷积网络相反的结构,它可以 将卷积网络的中间层的特征图映射回像素空间 ,从而展示出每一层所提取的特征和激活的模式。
通过反卷积网络,我们可以观察到 卷积网络的每一层都学习到了什么有用的知识,例如:
- 第一层:学习到了一些 简单的边缘和颜色 的检测器,类似于 传统的滤波器。
- 第二层:学习到了一些 由边缘和颜色组成的更复杂的形状和纹理 的检测器,例如 圆角、条纹、斑点等。
- 第三层:学习到了一些 由形状和纹理组成的更高级的特征 的检测器,例如 眼睛、鼻子、轮胎等。
- 第四层:学习到了一些 由高级特征组成的更具体的物体 的检测器,例如 狗、猫、人脸等。
- 第五层:学习到了一些 由具体物体组成的更抽象的类别 的检测器,例如 动物、汽车、飞机等。
