一、序列嵌入表示
序列是非结构化的任意字符串,对于计算机而言没有意义。
对于文本使用wordvec嵌入,可以将单词转化为n维度向量。
对于序列创建嵌入:
序列引入欧几里得空间,进而可以进行传统的机器学习和深度学习,例如kmeans聚类。
定义关键字:

SGT嵌入:不增加计算的情况下,轻松调整长期、短期模式的数量。
二、UMAP降维
降维的作用:识别高维空间中的关键结构并将它们保存在低维嵌入中来克服"维度诅咒"。
Projection ------通过投影点在平面、曲面或线上再现空间对象的过程或技术。也可以将其视为对象从高维空间到低维空间的映射。
Approximation------算法假设我们只有一组有限的数据样本(点),而不是构成流形的整个集合。因此,我们需要根据可用数据来近似流形。
Manifold------流形是一个拓扑空间,在每个点附近局部类似于欧几里得空间。一维流形包括线和圆,但不包括类似数字8的形状。二维流形(又名曲面)包括平面、球体、环面等。
Uniform------均匀性假设告诉我们我们的数据样本均匀(均匀)分布在流形上。但是,在现实世界中,这种情况很少发生。因此这个假设引出了在流形上距离是变化的概念。即,空间本身是扭曲的:空间根据数据显得更稀疏或更密集的位置进行拉伸或收缩。
1、学习流形结构
(1)寻找最近的邻居
使用 最近邻下降 算法找到最近的邻居,调整UMAP的n近邻 超参数指定想要使用多少个近邻点。试验超参数n_neighbors是很重要的,因为他控制UMAP如何平滑数据中的局部和全局的结构。
一个小的n_neighbors 值意味着我们需要一个非常局部的解释,准确地捕捉结构的细节。而较大的 n_neighbors 值意味着我们的估计将基于更大的区域,因此在整个流形中更广泛地准确。
(2)构建一个图
连接之前确定的最近邻构件图
假设点在流形上均匀分布,这表明它们之间的空间根据数据看起来更稀疏或更密集的位置而拉伸或收缩的。
- 空间的拉伸与收缩 :由于数据点分布的不均匀性,UMAP算法认为流形上的空间会根据数据点的分布情况而发生拉伸或收缩。在数据点密集的区域,空间会收缩,使得这些点之间的距离看起来更近;而在数据点稀疏的区域,空间会拉伸,使得这些点之间的距离看起来更远。这种空间的拉伸与收缩是为了更好地反映数据点之间的实际相似性。
- 距离度量的变化性 :传统的距离度量(如欧几里得距离)在整个空间中是固定的,但在UMAP算法中,距离度量不是固定的,而是根据数据点的分布情况在不同区域之间变化的。这种变化性的距离度量能够更好地适应数据的局部结构和全局结构。
- 可视化方法 :为了帮助理解这种变化性的距离度量,可以通过在每个数据点周围绘制圆圈或球体来进行可视化。在数据点密集的区域,由于空间收缩,这些圆圈或球体的大小会相对较小;而在数据点稀疏的区域,由于空间拉伸,这些圆圈或球体的大小会相对较大。通过这种可视化方法,可以更直观地看到距离度量在不同区域的变化情况。
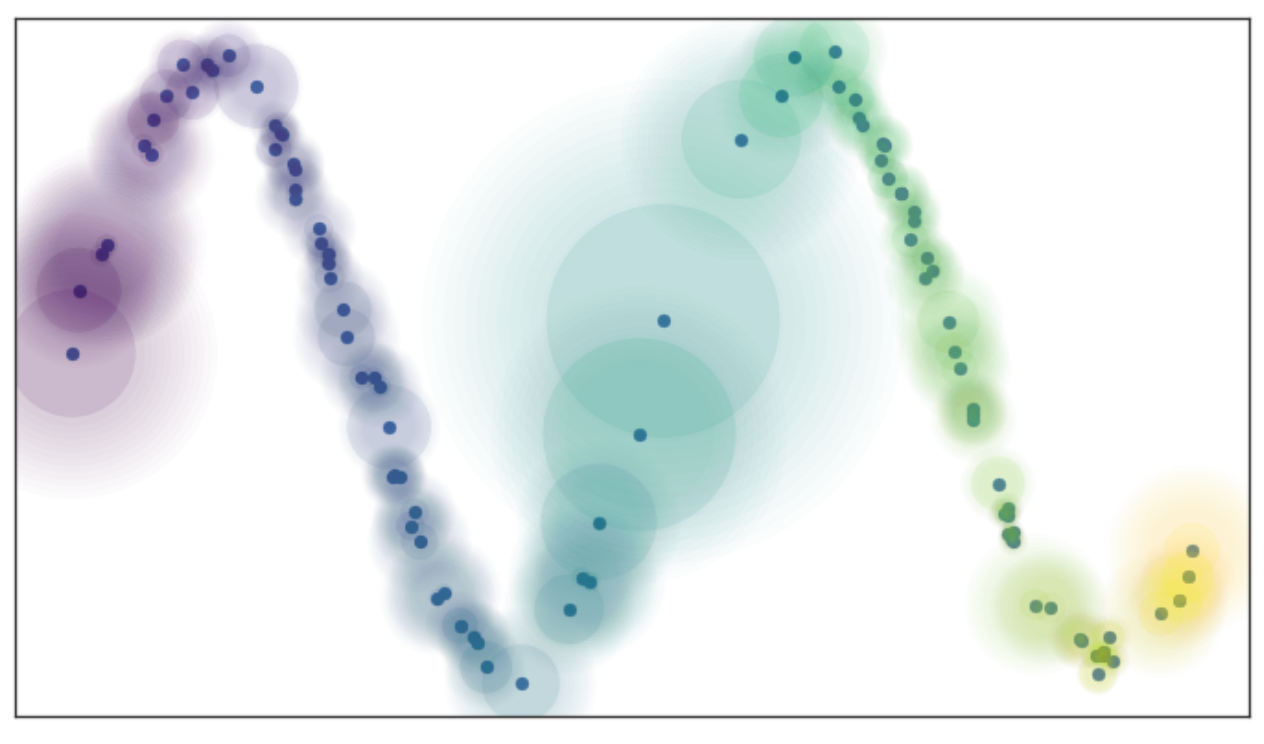
local_connectivity
要保证这个流形结构是相对完整、连贯的,而不是出现很多不连通的点。不连通点可以理解为在流形上出现了一些"断裂"或者"孤立"的部分,这些部分与其他部分没有连续的连接,这在很多情况下是不希望出现的,因为它可能会破坏整体的结构和性质,影响后续的分析或者应用。
这句话说明为了解决上述可能出现的不连通点的问题,引入了一个超参数local_connectivity。超参数是在学习算法开始之前就需要设置的参数,它不是通过数据学习得到的,而是由使用者根据经验和需求来设定的。这里的local_connectivity参数的作用就是用来控制流形结构的局部连通性,确保不会出现过多的不连通点。它有一个默认值为1,这意味着如果没有特别指定,这个参数就会采用1这个值来进行计算或者建模,当然使用者也可以根据实际情况调整这个值来达到更好的效果。
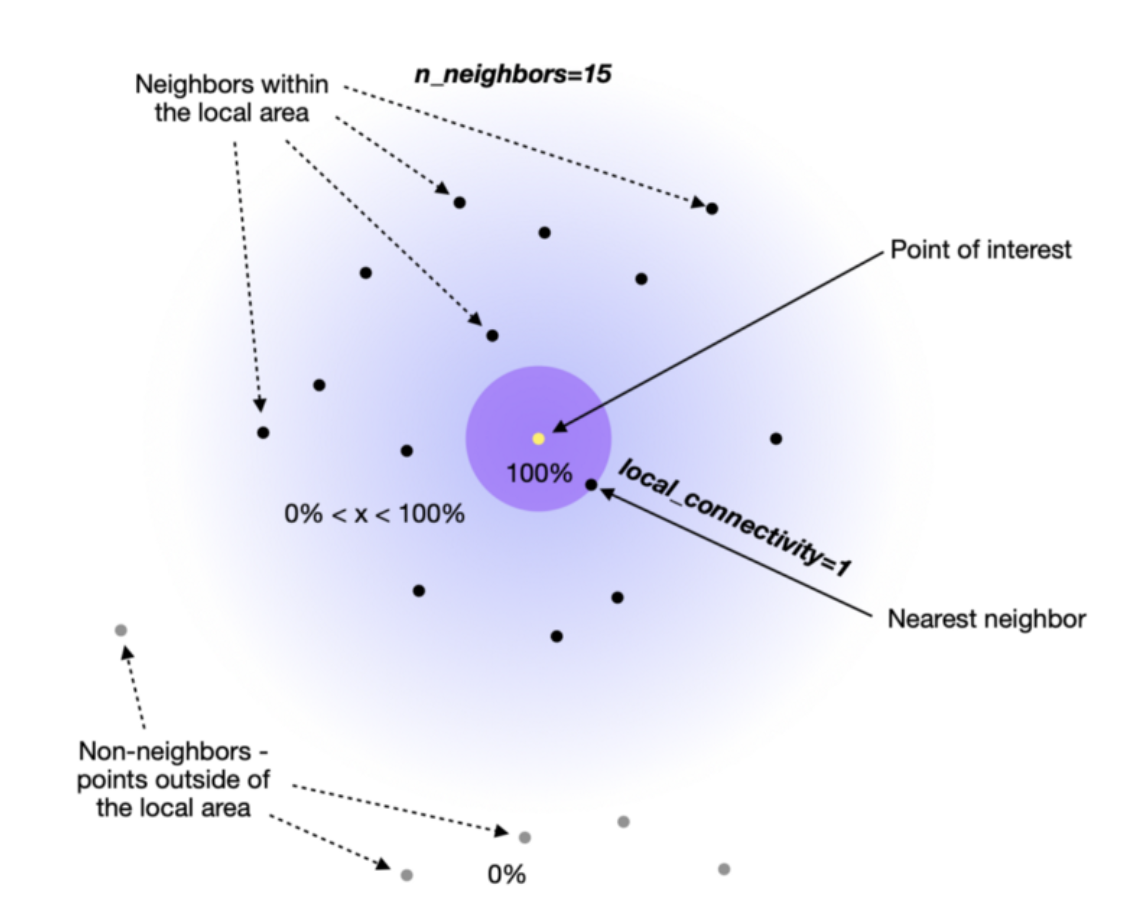
模糊区域
在构建邻域图的过程中,除了考虑每个点的最近邻点,还会考虑超出最近邻范围的一些点,这些点与中心点的连接关系用模糊的圆圈表示。这种模糊的表示方式说明,随着距离中心点越来越远,中心点与其他点之间存在连接关系的确定性会逐渐降低。也就是说,对于离中心点较远的点,不能像最近邻点那样非常确定地认为它们与中心点有连接,而是存在一定的不确定性。
-
local_connectivity(默认值为1):这个参数可以看作是连接数量的下限。当设置为1时,意味着在高维空间中,每个点至少会与另一个点建立连接关系,确保了邻域图中不会出现孤立的点,使得整个流形结构能够保持一定的连通性,避免出现许多不连通的点,从而能够更好地学习流形的整体结构。
-
n_neighbors(默认值为15):这个参数可以看作是连接数量的上限。它表示在构建图时,一个点直接连接到的邻居数量最多为这个值。也就是说,一个点直接连接到第16个以上的邻居的可能性为0%,因为这些点超出了UMAP在构建图时考虑的局部区域范围。这个参数控制了局部邻域的大小,进而影响UMAP如何平衡数据中的局部和全局结构。较小的n_neighbors值会使UMAP更关注局部结构,更准确地捕捉细节;较大的n_neighbors值会使UMAP在更大范围内进行估计,更广泛地反映整个流形的结构。
-
2 到 15:在这个范围内的点,与中心点的连接关系有一定的确定性,但这个确定性不是100%,也不是0%,而是介于两者之间。具体来说,一个点连接到它的第2个到第15个邻居的可能性是存在的,但随着序号的增加,这种可能性会逐渐降低。这种模糊的连接关系反映了数据在流形上的分布特性,即点与点之间的距离和连接关系并不是固定不变的,而是根据数据的分布情况而变化的。
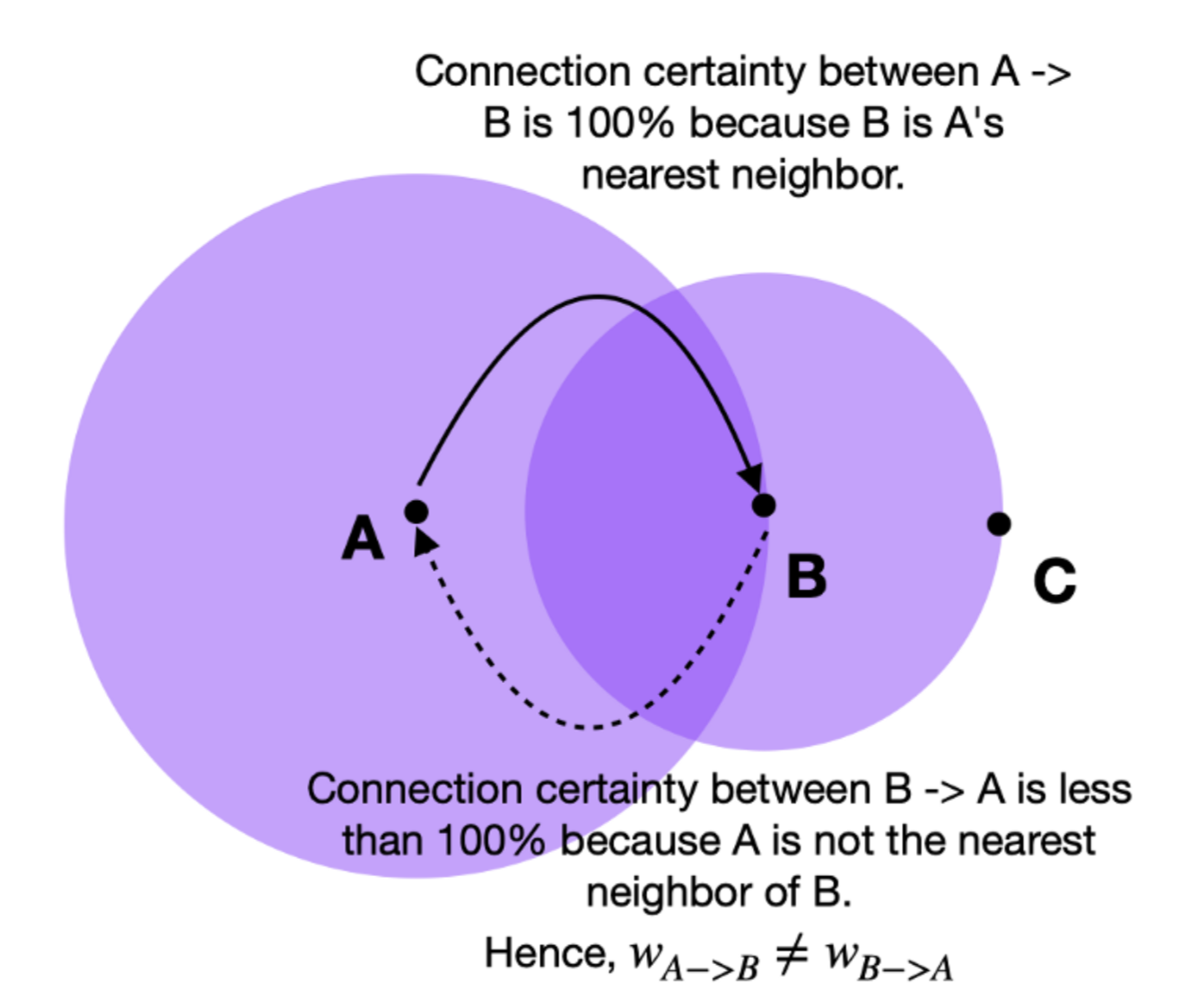
边的合并
连接确定性是通过边权重(w)来表达的。
由于我们采用了不同距离的方法,因此从每个点的角度来看,我们不可避免地会遇到边缘权重不对齐的情况。 例如,点 A→B 的边权重与 B→A 的边权重不同。
因为使用了不同的距离计算方法,所以在考虑每个点时,就会出现从一个点到另一个点的边权重与从那个点返回的边权重不一致的情况。比如,从点 A 到点 B 的边权重和从点 B 到点 A 的边权重不一样。
如果我们想将权重为 a 和 b 的两条不同的边合并在一起,那么我们应该有一个权重为 + − ⋅ 的单边。 考虑这一点的方法是,权重实际上是边(1-simplex)存在的概率。 组合权重就是至少存在一条边的概率。
最后,我们得到一个连接的邻域图,如下所示:
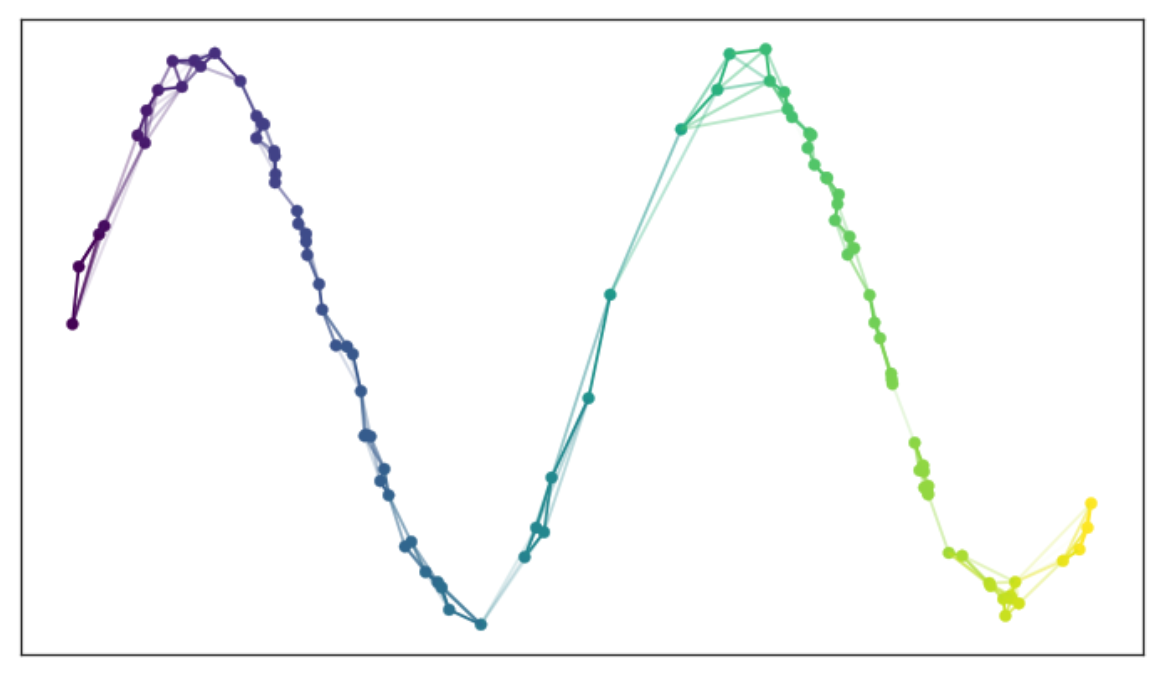
2、寻找低维表示
从高维空间学习近似流形后,UMAP 的下一步是将其投影(映射)到低维空间。
(1)最小距离
不希望在低维空间表示中改变距离。相反,我们希望流形上的距离是相对于全局坐标系的标准欧几里得距离。
从可变距离到标准距离的转换的转换也会影响与最近邻居的距离。因此,我们必须传递另一个名为 min_dist(默认值=0.1)的超参数来定义嵌入点之间的最小距离。
(2)最小化成本函数(Cross-Entropy)
指定最小距离后,该算法可以开始寻找较好的低维流形表示。 UMAP 通过最小化以下成本函数(也称为交叉熵 (CE))来实现:
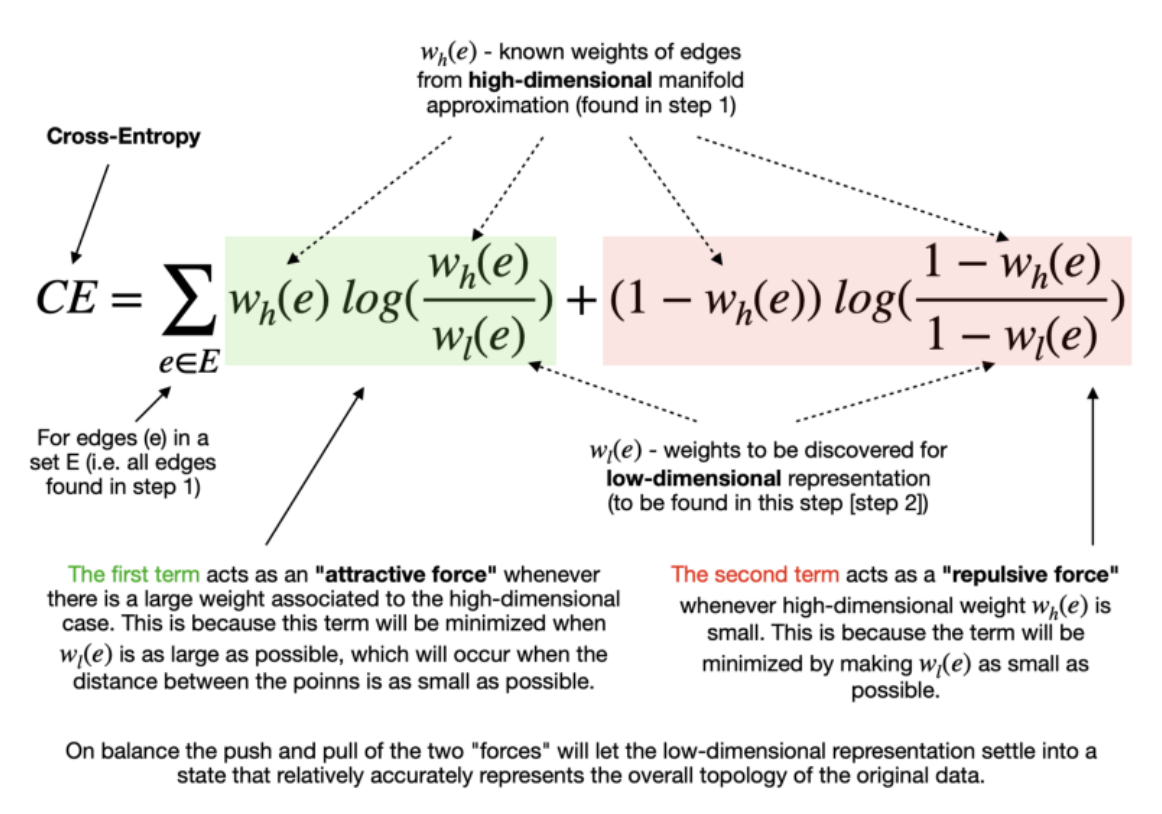
最终目标是在低维表示中找到边的最优权值。这些最优权值随着上述交叉熵函数的最小化而出现,这个过程是可以通过随机梯度下降法来进行优化的
------小狗照亮每一天
20250930