数据结构入门 (三)：链表的时空博弈 —— 循环链表与哑节点详解

Algo-hx2025-10-01 14:11

目录

引言：链表的时空博弈

上一篇文章我们初步了解了链式存储结构，同时对带头节点的链表的核心操作进行了详细分析。

单向链表的核心竞争力在于其插入和删除操作的极高效率，而这两个操作的思路其实是差不多的，都是找到前置节点。

c 复制代码 
// 插入
new_node->next = p->next;
p->next = new_node;
// 删除
tmp = p->next;
p->next = tmp->next;
free(tmp);

为什么说带头节点的链表会更好一些呢？原因就在于头节点使得链表中的所有节点都能找到前置节点，我们的代码也实现了完美的统一。

但这样也会存在一个问题，那就是对空间的浪费 。因为头节点并不存储任何有效数据，但它依然要占用一个完整节点大小的内存空间，尤其在数据域越大的时候越明显。这个问题是对空间效率的极致追求。为了节省这一个节点的空间，我们是否愿意接受更复杂的代码逻辑？这便是我们今天探讨的第一个内容------带头指针的单向链表。

同时，当我们使用单向链表时，访问表尾的代价是O(n)，代价太高了，而且到了表尾就必须掉头，非常低效！这个问题反映了对时间效率的极致追求。为了解决这个问题，我们将探索更加优雅的形态------单向循环链表。

一、哑节点------一个临时的头节点

为了节省一个节点的空间，我们选择不使用头节点，让头指针head直接指向第一个存储真实数据的节点（首元节点）。

图1 带头指针的单向链表

这种选择带来了"代码统一性"的缺失。对于首元节点来说没有前置节点，因此对于插入和删除操作就变成了特殊情况，必须单独处理，通常需要 if/else 来判断：

c 复制代码 
if (head == NULL) {
    // 链表为空
    head = new_node;
    new_node->next = NULL;
} else {
    // 链表非空
    new_node->next = head;
    head = new_node;  
}

需要if判断，相比较带头节点的链表麻烦多了。

dummy节点的巧妙运用：让特殊操作变通用

有没有办法让代码更简洁？答案是有的。实际上，带头节点的链表和带头指针的链表区别只是head指针指向不同，带头节点的链表head指针指向不含有效数据的头节点，而带头指针的链表head指针指向含有效数据的第一个节点。

清楚了这一点，我们可以效仿头节点，也就是在我们的第一个节点前引入一个虚拟头节点dummy，存入栈中。如此一来，所有的操作又变成带头节点的链表那一套了。

通过这个临时工，我们在操作期间把带"头指针的单向链表"伪装为"带头节点的单向链表"，使得所有操作逻辑再次回归统一。这是典型的"以空间换便捷，但用完即还"的编程智慧。

二、带头指针链表的完整实现

1.定义结构体

这里链表的节点结构和带头节点的链表是一样的。为了简化代码，我们可以创建一个common.h文件。写入：

c 复制代码 
typedef int Element_t;
// 1.定义链表节点结构
typedef struct _node {
    Element_t val;
    struct _node *next;
} node_t;

然后在带头指针的链表的头文件：

c 复制代码 
#include "common.h"

// 2.定义链表头结构，只保存头指针
typedef struct {
    node_t *head;
    int count;
} ChainList_t;

// 3.链表头放到数据区，也就是全局变量
void initChainList(ChainList_t *table);
void destroyChainList(); // 销毁该链表的元素区域，头不管

int insertChainListHeader(ChainList_t *table, Element_t val);
int insertChainListPos(ChainList_t *table, int pos, Element_t val);

int deleteChainListPos(ChainList_t *table, Element_t val);

void showChainList(const ChainList_t *table);

2.初始化链表

c 复制代码 
void initChainList(ChainList_t* table) {
    table->count = 0;
    table->head = NULL;
}

3.从链表头部插入（巧用dummy节点）

c 复制代码 
int insertChainListHeader(ChainList_t* table, Element_t val) {
	node_t dummy;  // 创建一个哑节点
	dummy.next = table->head;  // 指向头指针指向的第一个节点

	node_t *p = &dummy;  // 创建指针p指向dummy地址
	node_t *new_node = malloc(sizeof(node_t));  // 分配内存,这块内存的地址赋给new_node
	if (new_node == NULL) {
		return -1;
	}

	new_node->val = val;
	new_node->next = p->next;
	p->next = new_node;

	table->count++;
	table->head = dummy.next;
	return 0;
}

4.从链表任意位置插入

c 复制代码 
int insertChainListPos(ChainList_t *table, int pos, Element_t val) {
	node_t dummy;
	dummy.next = table->head;

	// 1.判断边界值
  if (pos < 0 || pos > table->count) {
		printf("insert pos invalid\n");
     return -1;
	}
	// 2.找到pos - 1索引的节点首地址
	node_t *p = &dummy;
   int index = -1;
   while (index < pos - 1)
   {
       p = p->next;
       ++index;
   }
   node_t *new_node = malloc(sizeof(node_t));
   new_node->val = val;
   new_node->next = p->next;
   p->next = new_node;
   ++table->count;

   table->head = dummy.next;
   return 0;
}

5.查看链表

c 复制代码 
void showChainList(const ChainList_t* table) {
    node_t *p = table->head;
    printf("count: %d\n", table->count);
    while (p) {
        printf("%d\t", p->val);
        p = p->next;
    }
    printf("\n");
}

6.删除任意位置的链表节点

c 复制代码 
int deleteChainListPos(ChainList_t* table, Element_t val)
{
    node_t dummy;
    dummy.next = table->head;

    node_t *p = &dummy;
    while (p->next && p->next->val != val)
    {
        p = p->next;
    }
    if (p->next == NULL)
    {
        return -1;
    }
    node_t *tmp = p->next;
    p->next = tmp->next;
    free(tmp);
    --table->count;

    table->head = dummy.next;
    return 0;
}

7.销毁链表

c 复制代码 
void destroyChainList(ChainList_t* table)
{
    node_t dummy;
    dummy.next = table->head;

    node_t *p = &dummy;
    node_t *tmp;
    while (p->next)
    {
        tmp = p->next;  
        p->next = tmp->next;
        free(tmp);
        --table->count;
    }
    printf("LinkList have %d node!\n", table->count);
    table->head = NULL;
}

8.测试函数

c 复制代码 
// 带头指针的单向链表测试
int test02()
{
    ChainList_t stu1;  // 定义了全局变量stu1，空间静态分配
    initChainList(&stu1);

    for (int i = 0; i < 10; i++)
    {
        insertChainListHeader(&stu1, i + 100);
    }
    showChainList(&stu1);
    insertChainListPos(&stu1, 2, 220);
    showChainList(&stu1);

    deleteChainListPos(&stu1, 104);
    showChainList(&stu1);
    destroyChainList(&stu1);
    printf("==================\n");
    showChainList(&stu1);
    return 0;
}

int main()
{
    test02();
    return 0;
}

结果是：

三、妙用循环------让链表"首尾相连"

我们已经把空间优化到了极致，下面我们来关注时间。

在有头节点的单向链表中，我们访问第一个节点只需要O(1)的时间，但如果想要访问最后一个节点，则需要O(n)的时间，因为我们需要从头开始将单链表的所有节点访问一遍。

c 复制代码 
node_t *p = head;
while (p->next) { // 看的是自己的下一个节点，适合插入、删除
	p = p->next; 
}

node_t *p = head;
while (p) { // 看的的是自己，适合遍历，以及对当前节点进行操作。
	p = p->next; 
}

当我们尾插时，实际上是很麻烦的，需要进行非常多次的循环，但是尾插的场景又很常见，怎么解决这个问题呢？再进一步，如果我们已经到达尾部了，这时候如果需要重新对头部进行操作，怎么办？

显然，单纯的单向链表有很多局限性。针对第一个问题，我们考虑从头节点入手。我们知道，头节点通常存储下一个节点的指针，如果让它储存指向最后一个节点的尾指针，那么尾插法就可以直接使用这个指针进行操作，而不需要遍历整个链表。对于第二个问题，我们让尾节点不要指向NULL，而是指向第一个节点，这样我们就可以从尾部回到头部。而这个尾节点的next指针指向第一个节点的链表，就是单向循环链表 。

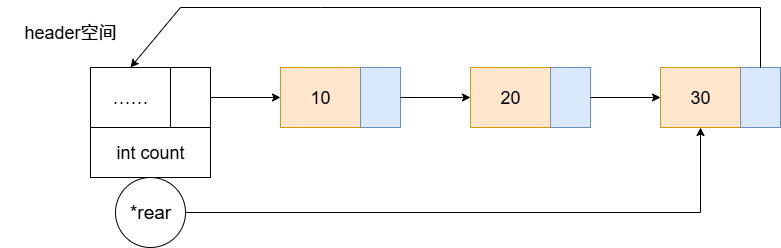
图2 带头节点的单向循环链表


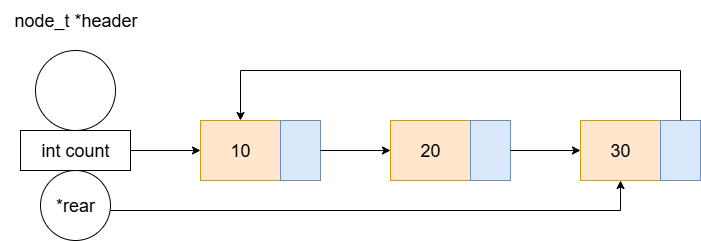
图3 带头指针的单向循环链表

"循环结构 + 尾指针"的组合完美解决了原本单向链表的痛点，它带来了以下好处：

  • 访问尾节点：通过rear指针，时间复杂度O(1)
  • 访问头节点：通过header.next指针，时间复杂度O(1)
  • 访问首元节点：通过rear->next指针（对带头节点的循环链表，是header->next，或者rear->next指向头节点，再header.next），时间复杂度O(1)

我们同时拥有了对链表两端的O(1)级别的访问能力。

四、带头节点单向循环链表的实现

以带头节点的单向循环链表为例。

1.定义结构体

c 复制代码 
// 定义节点结构
typedef int Element;
typedef struct _loop_node
{
    Element val;
    struct _loop_node *next;
} LoopNode;

// 定义单向循环链表的头结构
typedef struct
{
    LoopNode header; // 头节点
    LoopNode *rear; // 尾指针，指向链表最后一个节点
    int num;
} LinkLoopList;

// 初始化接口
void initLinkLoopList(LinkLoopList *link_loop);
// 插入（头插、尾插）
int insertLinkLoopHeader(LinkLoopList *link_loop, Element value);
int insertLinkLoopRear(LinkLoopList *link_loop, Element value);
// 遍历显示
void showLinkLoop(const LinkLoopList *link_loop);
// 删除
int deleteLinkLoopList(LinkLoopList *link_loop, Element value);
// 释放整个数据域，不释放头
void destroyLinkLoopList(LinkLoopList *link_loop);

2.初始化

空循环链表的头节点和尾指针都指向头节点自身，形成一个最小的环。

c 复制代码 
void initLinkLoopList(LinkLoopList *link_loop)
{
    link_loop->header.next = link_loop->rear = &link_loop->header;
    link_loop->num = 0;
}

3.头插法

c 复制代码 
int insertLinkLoopHeader(LinkLoopList* link_loop, Element value)
{
    // 1. 先有新节点
    LoopNode *node = malloc(sizeof(LoopNode));
    if (node == NULL)
    {
        return -1;
    }
    node->val = value;
    node->next = link_loop->header.next;
    link_loop->header.next = node;

    // 2. 判断尾指针是否需要更新
    if (link_loop->rear == &link_loop->header)
    {
        link_loop->rear = node;
    }
    link_loop->num++;
    return 0;
}

4.尾插法

尾插法是这种结构的最大优势所在，代码极其高效。

c 复制代码 
int insertLinkLoopRear(LinkLoopList* link_loop, Element value)
{
    // 1. 先有新节点
    LoopNode *node = malloc(sizeof(LoopNode));
    if (node == NULL)
    {
        return -1;
    }
    node->val = value;
    node->next = link_loop->rear->next;
    link_loop->rear->next = node; // 更新最后一个节点
    link_loop->rear = node; // 更新尾指针
    ++link_loop->num;
    return 0;
}

5.遍历链表

c 复制代码 
void showLinkLoop(const LinkLoopList* link_loop)
{
    LoopNode *node = link_loop->header.next; // 从第一个有效节点开始
    while (node != &link_loop->header) // 直到遍历到头节点
    {
        printf("\t%d ", node->val);
        node = node->next;
    }
    printf("\n");
}

6.删除链表节点

c 复制代码 
int deleteLinkLoopList(LinkLoopList* link_loop, Element value)
{
    LoopNode* node = &link_loop->header;

    while (node->next != &link_loop->header && node->next->val != value)
    {
        node = node->next;
    }
    if (node->next->val == value)
    {
        LoopNode *tmp = node->next;
        node->next = tmp->next;
        free(tmp);
        --link_loop->num;
    }
    else
    {
        printf("error\n");
    }
    return 0;
}

7.销毁链表

c 复制代码 
void destroyLinkLoopList(LinkLoopList* link_loop)
{
    LoopNode *node = link_loop->header.next;
    while (node != &link_loop->header)
    {
        LoopNode *tmp = node;
        node = node->next;
        free(tmp);
        --link_loop->num;
    }
    printf("Table has %d element now!\n");
}

8.测试函数

c 复制代码 
void test01()
{
    LinkLoopList table;
    initLinkLoopList(&table);

    for (int i = 0; i < 10; ++i)
    {
        insertLinkLoopRear(&table, i + 100);
    }
    showLinkLoop(&table);
    printf("==========================\n");
    deleteLinkLoopList(&table, 106);
    showLinkLoop(&table);

    destroyLinkLoopList(&table);
}
int main()
{
    test01();
    return 0;
}

结果为：

五、总结：没有银弹，只有取舍

这篇文章，我们探索了单向链表的两种升级形态：

  1. 带头指针的链表：通过巧妙的dummy节点引用，追求空间效率的同时，也不失代码的优雅
  2. 带尾指针的循环链表：通过"首尾相连"和尾指针，获得了对链表两端的高效访问能力，追求时间效率

这再次印证了数据结构世界的一个核心法则：没有银弹，只有永恒的取舍。你想要节省一点空间，可能就需要付出更复杂逻辑的代价；你想要获得更快的访问速度，就需要引入循环结构和额外的尾指针。

我们已经征服了空间效率和时间效率，但这些链表，仍然存在一个根本性的束缚：它们都是单行道。我们始终无法轻松的回头看。

为了实现真正的来去自如，我们需要为链表开辟一条"逆行车道"。这将是我们下一段旅程的目标------双向链表。

相关推荐
南莺莺2 小时前
树的存储结构
数据结构·算法·树
Sapphire～2 小时前
重学JS-009 --- JavaScript算法与数据结构（九）Javascript 方法
javascript·数据结构·算法
aramae3 小时前
链表理论基础
数据结构·c++·算法·leetcode·链表
2401_845417453 小时前
哈希表原理详解
数据结构·哈希算法·散列表
chao_7894 小时前
Union 和 Optional 区别
开发语言·数据结构·python·fastapi
hope_wisdom6 小时前
C/C++数据结构之用数组实现栈
c语言·数据结构·c++·数组·栈
范特西_6 小时前
数组的最大美丽值
数据结构·算法
蒙奇D索大7 小时前
【数据结构】图论核心应用：关键路径算法详解——从AOE网到项目管理实战
数据结构·笔记·学习·考研·算法·图论·改行学it
学c语言的枫子7 小时前
数据结构——Dijkstra算法
数据结构·算法
热门推荐
01OpenSpeedy简介02在国行 macOS 下用 DeepSeek 补齐 Xcode 26 的 AI 能力：问题、原因与 mitmproxy 解决方案（含可用脚本与安装教程）03GitHub 镜像站点04UV安装并设置国内源05KGG转MP3工具|非KGM文件|解密音频06UV 工具安装与国内镜像源配置指南07阿里最新开源Wan2.2-Animate-14B 本地部署教程：统一双模态框架，MoE架构赋能电影级角色动画与替换08Spec-Kit 使用指南09Linux下V2Ray安装配置指南1046个Nano-banana 精选提示词，持续更新中